加權馬爾可夫鏈在保定地區降雨量預測中的應用

顧志華，商秀印

（河北農業大學理學院，河北保定 071001）

“馬爾可夫模型”是俄國數學家Markov在1966年最早提出的，經過幾十年不斷的發展，Markov過程已成為隨機過程的一個重要分支.馬爾可夫鏈可以描繪一個隨機變化的動態系統，它根據狀態間的轉移概率來推測一個系統的未來的發展變化.

降雨過程受氣象等條件的影響，存在大量的隨機性.如果能夠比較準確地預測降雨量，可以為農業等行業的決策提供重要依據.針對保定地區1960—2010年的年降雨量資料，采用均值－標準差分級法，建立了適用于保定地區的年降雨量分級標準.并用加權馬爾可夫鏈對保定地區2011和2012年年降雨量狀態進行了預測，考慮到馬爾可夫鏈只能預測出降雨量的某一區間，故本文又結合模糊集理論對2011和2012年的降雨量進行了預測.

1 保定地區年降雨量狀態的確定

設降雨量序列為X1，X2，…，Xn，采用均值－標準差分級法，將各年降雨量進行狀態分級，分為枯水年、偏枯年、平水年、偏豐年和豐水年5個狀態.保定地區1960—2010年降雨量的均值＝522.65，標準差S＝148.46.年降雨量分級見表1，區內1960—2010年降雨量序列及其狀態見表2.

表1 年降雨量分級表Tab.1 Annual rainfall classification

表2 年降雨量序列及其狀態Tab.2 Annual precincepition sequence and state

2 加權馬爾可夫鏈預測過程

1）采用均值－標準差分級法，確定狀態空間，以此來確定序列中各指標值的狀態.

2）符號表示.

fij為研究序列X1，X2，…，Xn中從i狀態出發，經過一步轉移到達狀態j的頻率.＝為轉移頻率矩陣為邊緣頻率（m為狀態值）.

3）對研究序列進行馬氏性檢驗.

4）計算序列各階自相關系數rk.

式中，Xi為第i時段的指標值—指標值平均值.

5）把各階自相關系數規范化，即

式中，m為預測時需要計算到的最大階數.

6）分別以前面若干時段的指標值為初始狀態，結合其相應的各階轉移概率矩陣，即可預測出該時段指標值的狀態，k為滯時（步長）.

7）將同一狀態的各預測概率加權和作為指標值處于該狀態的預測概率，即所對應的即為該時段指標值的預測狀態.

8）對各狀態分別賦予相應的權重，即權重集ω＝｛ω1，ω2，ω3，ω4，ω5｝，其中為最大概率的作用系數，這里取2.級別特征值如果年降雨量預測狀態為i，且H≥i，則年降雨量的預測值為如果H＜i，則預測值為其中Ti，Bi分別為狀態區間值的上限和下限.

3 加權馬爾科夫鏈模型在保定地區降雨量預測中的應用

1）進行馬氏檢驗

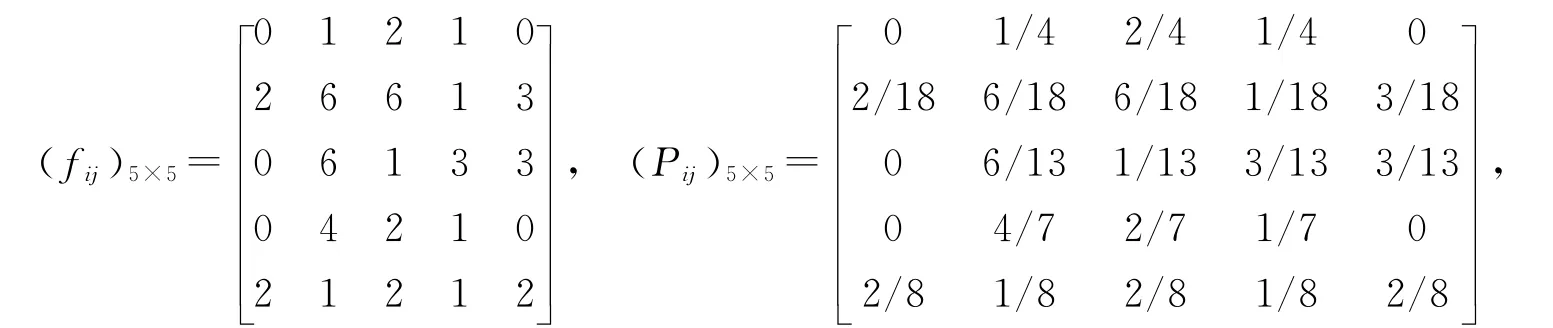
2）各階自相關系數及權重的計算（表3、表4）

表3 1～5階自相關系數及權重Tab.3 1～5the self correlation coefficients and the weights

表4 2～6階自相關系數及權重Tab.4 2～6the self correlation coefficients and the weights

3）根據2004—2008年的年降雨量數據，采用1～5階權重系數，對2009年的降雨量狀態進行預測，結果見表5.

表5 2009年的降雨量狀態預測（利用表3）Tab.5 Predication of annual rainfall states in 2009（with tab.3）

由上表知max（P）＝0.428，根據模糊集理論，由公式預測2009年降雨量340.68mm，實際降雨

i量為355.50mm，相對誤差為4%.

根據2003—2007年的年降雨量數據，采用2～6階權重系數，對2009年的降雨量狀態進行預測，結果見表6.

表6 2009年的降雨量狀態預測（利用表4）Tab.6 Predication of annual rainfall states in 2009（with tab.4）

由上表知max（Pi）＝0.353，此時i＝2，即2009年年降雨量預測狀態為2，而2009年年降雨量實際狀態也為2，和預測狀態相吻合.根據模糊集理論，由公式預測2009年降雨量為371.88mm，實際降雨量為355.50mm，相對誤差為4%.

根據2005—2009年的年降雨量數據，采用1～5階權重系數，對2010年的降雨量狀態進行預測，結果見表7.

表7 2010年的降雨量狀態預測（利用表3）Tab.7 Predication of annual rainfall states in 2010（with tab.3）

由上表知max（Pi）＝0.293，此時i＝2，即2010年年降雨量預測狀態為2，而2010年年降雨量實際狀態也為2，和預測狀態相吻合.根據模糊集理論，由公式預測2010年降雨量為437.78mm，實際降雨量為395.00mm，相對誤差為10%.

根據2004—2008年的年降雨量數據，采用2～6階權重系數，對2010年的降雨量狀態進行預測，結果見表8.

由上表知max（Pi）＝0.276，此時i＝2，即2010年年降雨量預測狀態為2，而2010年年降雨量實際狀態也為2，和預測狀態相吻合.根據模糊集理論，由公式預測2010年降雨量為424.85mm，實際降雨量為395.00mm，相對誤差為7%.

表9 實際與預測結果Tab.9 Actual and predictive results

4 結論

無論是1～5階權重還是2～6階權重來預測降雨量，誤差控制在10%以內，因此更加說明了加權馬爾可夫鏈預測模型的可靠度.重復以上方法，即根據1960—2010年年降雨量序列，以2006—2010年作為初始年，用1～5階權重系數預測出2011年年降雨量為468.77mm，用2～6階權重系數預測出2012年的降雨量為618.51mm.

［1] 王濤，錢會，李賠月.加權馬爾可夫鏈銀川地區降雨量預測中的應用［J］.南水北調與水利科技，2010，1（8）：78－81.WANG Tao，QIAN Hui，LI Peiyue.Prediction of precipitation based on the weighted Markov chain in Yinchuan area［J］.South－to－North Water Transfers and Water Science Technology，2010，1（8）：78－81.

［2] 謝波濤.臺風颶風影響海區固定式平臺設計標準及服役期安全度風險分析［D］.青島：中國海洋大學，2010.XIE Botao.The analysis of the design criterion and dynamic reliability assessment of existing platform in Typhoon／hurricane affected region［D］.Qingdao：Ocean University of China，2010.

［3] 夏樂天.馬爾可夫鏈預測方法及其在水文序列中的應用研究［D］.南京：河海大學，2005.XIA Letian.Research of Markov chain prediction method and its application on Hydrology series［D］.Nanjing：Hohai U－niversity，2005.

［4] 仲遠見，李靖，王龍.改進馬爾可夫鏈降雨量預測模型的應用［J］.濟南大學學報：自然科學版，2009，23（4）：402－405.ZHONG Yuanjian，LI Jing，WANG Long.Precipitation predicting model based on improved Markov chain［J］.Journal of University of Jinan：Science Technology，2009，23（4）：402－405.

［5] 姜昊.灰色馬爾可夫預測模型在臺風誘發災害研究中的應用［D］.青島：中國海洋大學，2009.JIANG Hao.The Application of Grey－Markov forecasting model in the research of Typhoon induced disasters［D］.Qingdao：Ocean University of China，2009.

［6] 李娟，張維江，馬軼.滑動－平均馬爾可夫模型在降水預測中的應用［J］.水土保持研究，2005，12（6）：196－198.LI Juan，ZHANG Weijiang，MA Yi.Application of moving Average－Markov chain in the prediction of precipitation［J］.Research of Soil and Water Conservation，2005，12（6）：196－198.

［7] 孫才志，林學鈺.降水預測的模糊權馬爾可夫模型及應用［J］.系統工程學報，2003，18（4）：295－298.SUN Caizhi，LIN Xueyu.Research on fuzzy Markov chain model with weights and its application in predicting the precipitation state［J］.Journal of Systems Engineering，2003，18（4）：295－298.

［8] 童精勤.年降雨量的預測研究［J］.武漢理工大學學報，2008，30（7）：99－102.TONG Jingqin.Research of predicting the precipitation in one year［J］.Journal of Wuhan University of Technology，2008，30（7）：99－102.

［9] 馮耀龍，韓文秀.權馬爾可夫鏈在河流豐枯狀況預測中的應用［J］.系統工程理論與實踐，1999（10）：89－98.FENG Yaolong，HAN Wenxiu.The application of weighted Markov－Chain to the prediction of River Runoff State［J］.Systems Engineering－Theory ＆Practice，1999（10）：89－98.