利用二階導數構造的數值積分公式

陳亞婷，冀德剛，賈鸝，張雅靜

（河北農業大學理學院，河北保定 071001）

在工業生產和科學實踐中，常常需要計算大量的積分問題.有些數值方法，如微分方程和積分方程的求解，也都和積分計算相聯系.依據微積分基本定理，對于積分只要找到被積函數f（x）的原函數F（x），便可利用牛頓－萊布尼茨公式但實際使用這種求積方法往往有困難，因為大量的被積函數，其原函數不能用初等函數表示，故不能用上述公式計算；有些函數，即使能求得原函數的積分有時計算也是十分困難.另外，當f（x）是由測量或數值計算給出的一張數據表，牛頓－萊布尼茨公式也不能直接應用.因此有必要研究積分的數值計算方法［1－3］.

本文在文獻［4－11］基礎上，利用二階導數，構造了一種新的具有7次代數精度的數值積分公式，并給出了其復合公式和加速公式，對于每個公式也進行了余項研究和誤差分析，最后通過幾個典型的例子驗證本文得到的公式的有效性.

1 構造公式

首先假定被積函數f（x）在積分區間［a，b］上足夠光滑，并且其在［a，b］上每一點處的二階導數都可求得.

在積分區間［a，b］上取其中點設已知被積函數f（x）在點上函數值f（b）和二階導數值構造如下的求積公式：

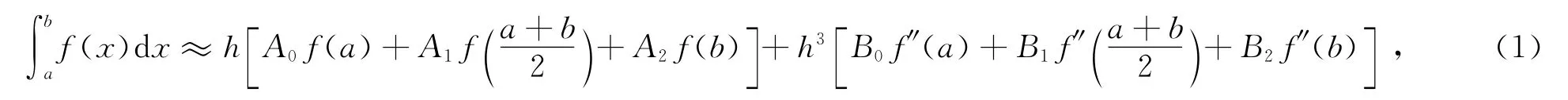
現需確定公式（1）的待定參數Ai，Bi（i＝0，1，2），使求積公式具有盡可能高的代數精度.令求積公式對f（x）＝1，x，x2，…，x6精確成立，可解得

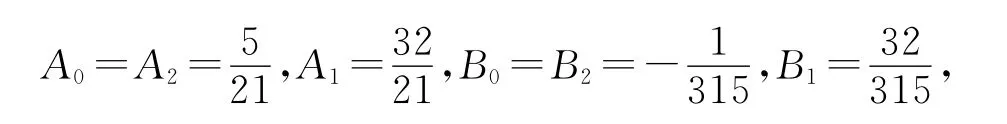
于是可得到求積公式

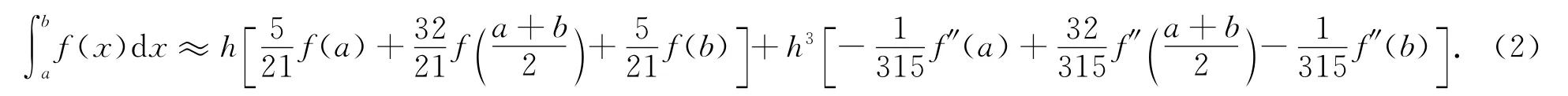
令f（x）＝x7，該公式也精確成立，但是f（x）＝x8時該公式不精確成立，因此該求積公式具有7次代數精度.

根據廣義皮亞諾定理，經計算得余項

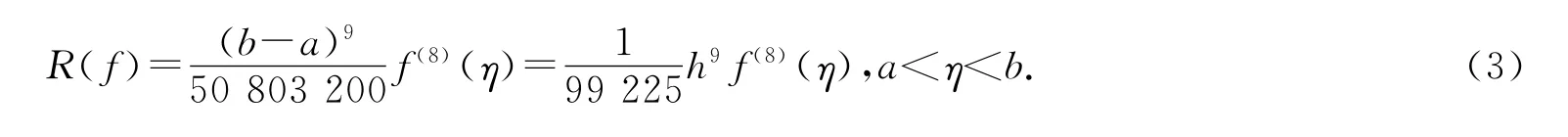
2 復合公式及其加速

將積分區間［a，b］分成2n等分，記節點x＝a＋ih，i＝0，1，2，…，2n，其中在每個小區間

i

1［x2i－2，x2i］（i＝1，2，…，n）上應用公式（2）得

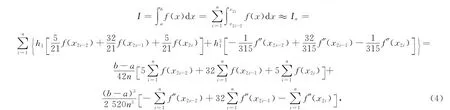
把式（4）整理即可得如下形式：

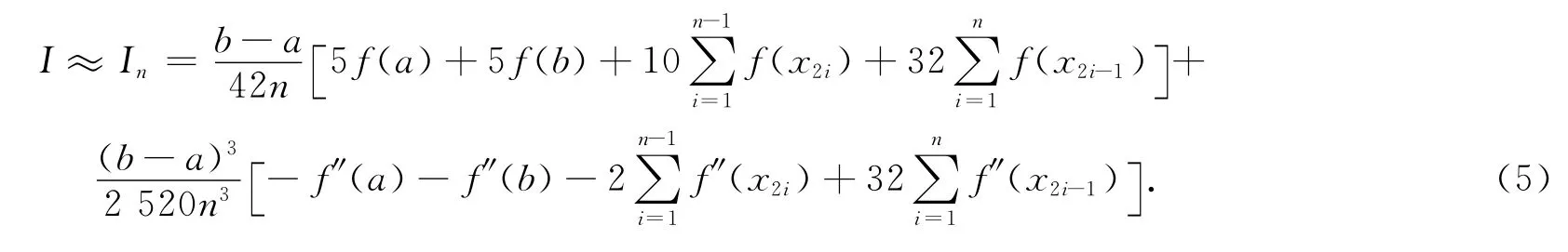
綜上知，當n→∞時，式（4）右端In收斂于積分即復合公式（4）收斂.假設f（x）∈C［8］［a，b］，則復合求積公式的余項為

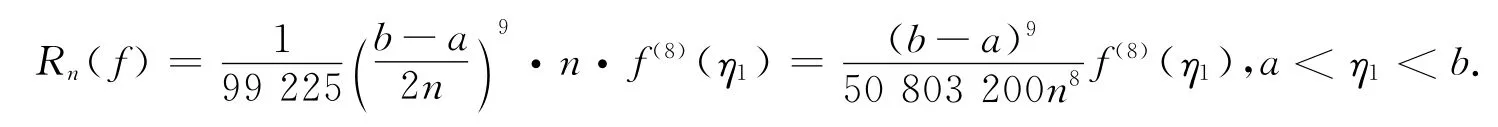
然后將積分區間［a，b］分成4n等分，記節點xi＝a＋ih1，（i＝0，1，2，…，2n）及＝，（i＝1，2，…，2n）.在每個小區間［x，x］和［x，x］（i＝1，2，…，n）上應用公式（2）得2i－22i－12i－12i

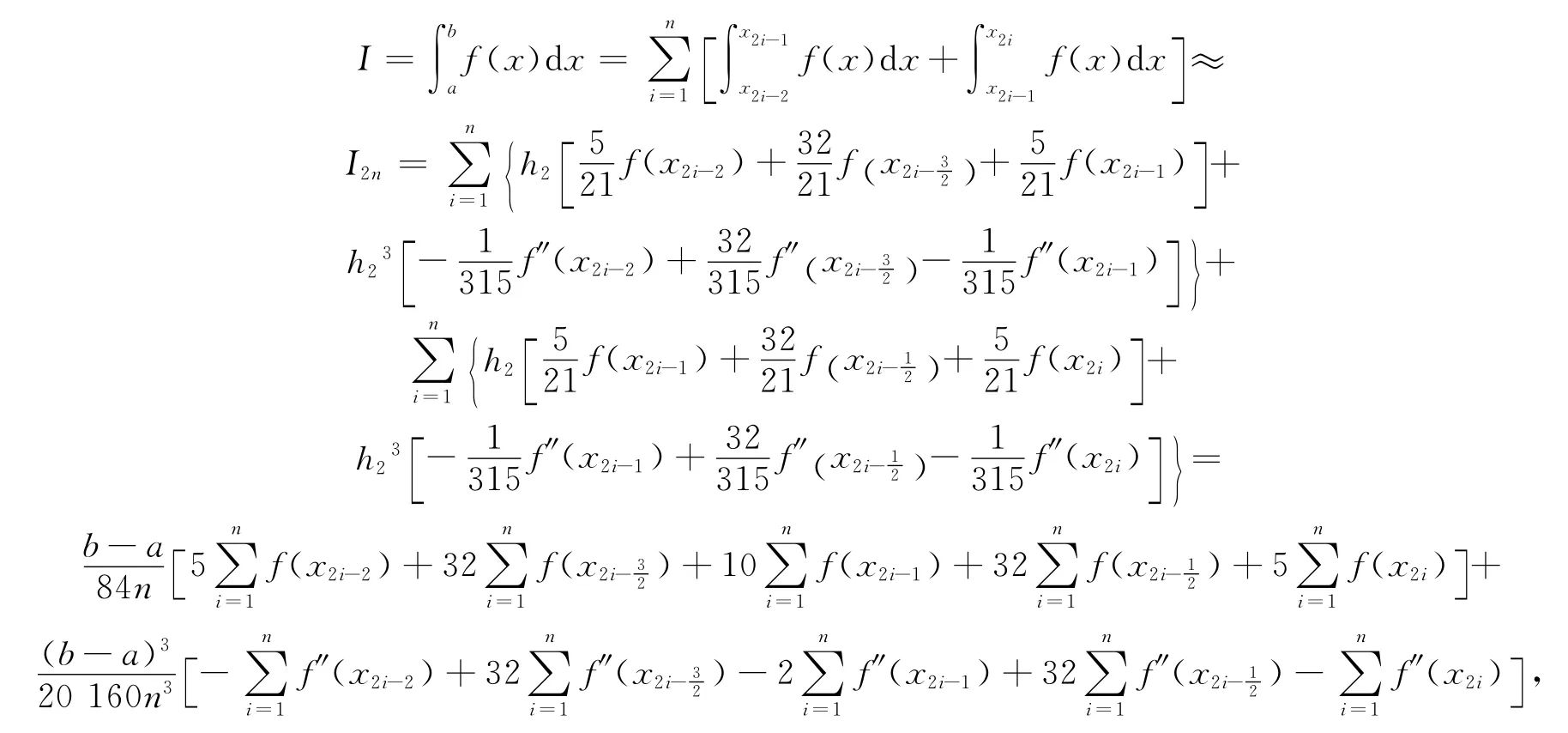
其余項

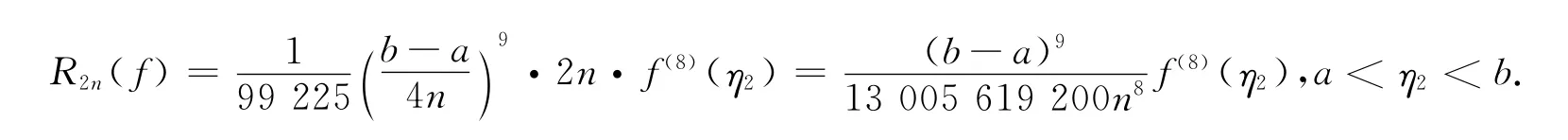
由假設f（x）∈C［8］［a，b］，并假定當n充分大時則有即I≈這里I表示真值.

記

則是比In和I2n更好的接近于I的近似值.其余項為

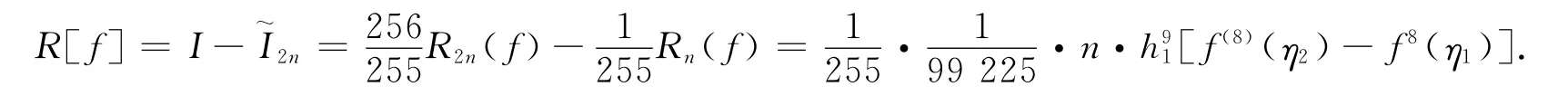
對于上述余項的估計，有如下定理.

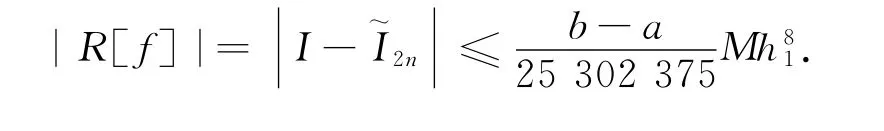
3 數值實驗

已知真值I＝0.946 083 070 367 18，

本文公式（2）：近似值為0.946 083 069 878 380，誤差為4.888 000 004 754 645×10－10.

本文公式（4）：n＝2時，近似值為0.946 083 070 365 313，誤差為1.869 542 824 855 863 0×10－12.

n＝4時，近似值為0.946 083 070 367 176，誤差為7.143 701 047 162 956 5×10－15.

n＝8時，近似值為0.946 083 070 367 183，誤差為7.274 861 290 056 10×10－17.

本文公式（6）：n＝2時

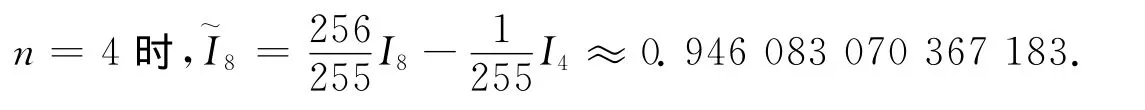
可見，如果保留到小數點后15位，該結果可以作為精確值的很好的近似.尤其對式（6），只需用n＝2情形計算即可達到很高的精度，計算量也較小.

已知真值I＝0.785 398 163 397 448，

本文公式（2）：近似值為0.785 439 682 539 683，誤差為4.151 914 223 435×10－5.

本文公式（4）：n＝2時，近似值為0.785 398 258 555 694，誤差為9.515 824 614 106 20×10－8.

n＝4時，近似值為0.785 398 163 395 992，誤差為1.456 088 112 965 87×10－12.

n＝8時，近似值為0.785 398 163 397 447，誤差為3.330 669 073 875 470×10－16.

4 結論

通過上面的數值計算結果表明：在計算數值積分時，本文構造的數值積分公式能很好地作為積分值的近似，而且精確程度較高.同時，所得到的積分公式還易于編程.本文的優點在于利用了較少的條件構造了一個高次代數精度的數值積分公式，由此用較少的計算量就可以達到精度的要求，因而在實際計算中有廣泛的應用.

［1] 李慶揚，王能超，易大義.數值分析［M］.北京：清華大學出版社，2008.

［2] 楊濤，王愛茹，王增輝.計算方法［M］.北京：中國水利水電出版社，2005.

［3] 陳公寧，沈家驥.計算方法導引［M］.北京：北京師范大學出版社，2009.

［4] 鄭華盛，唐經綸，危地.高精度數值積分公式的構造及其應用［J］.數學的實踐與認識，2007，37（15）：141－148.ZHENG Huasheng，TANG Jinglun，WEI Di.Constructions of high accurate numerical integration formula and its applications［J］.Mathematics in Practice and Theory，2007，37（15）：141－148.

［5] 徐偉，鄭華盛，李曦.一類高精度數值積分公式的構造［J］.數學的實踐與認識，2012，42（18）：207－215.XU Wei，ZHENG Huasheng，LI Xi.Constructions of new high accurate numerical integration formula［J］.Mathematics in Practice and Theory，2012，42（18）：207－215.

［6] 許江浩，陳志坤，劉斌.一個高精度數值積分公式［J］.四川理工學院學報，2011，24（2）：168－170.XU Jianghao，CHEN Zhikun，LIU Bin.A higher order accuracy numerical quadrature rule［J］.Journal of Sichuan University of Science and Engineering：Natural Science Edition，2011，24（2）：168－170.

［7] 吳新元.一個高精度數值積分公式［J］.計算物理，1988，5（4）：473－477.WU Xinyuan.A high accurate numerical integration formula［J］.Journal of Computational Physics，1988，5（4）：473－477.

［8] 吳新元，吳宏偉.一個新的高精度二重數值積分公式［J］.計算物理，1991，8（4）：437－441.WU Xinyuan，WU Hongwei.A high accurate numerical integration formula［J］.Journal of Computational Physics，1991，8（4）：437－441.

［9] 婁愛芳，胡軍浩.一個新的數值積分公式［J］.數學理論與應用，2010，30（4）：72－74.LOU Aifang，HU Junhao.A type of integrating formula［J］.Mathematical Theory and Applications，2010，30（4）：72－74.

［10] 劉學飛.復化Newton－Cotes公式及其誤差［J］.重慶三峽學院學報，2007，23（3）：52－54.LIU Xuefei.On compound Newton－Cotes multi－integral formula and their errors［J］.Journal of Chongqing Three Gorges University，2007，23（3）：52－54.

［11] 楊錄峰，馬寧，趙雙鎖.一種變步長和變階計算的自適應數值積分算法［J］.云南民族大學學報：自然科學版，2011，20（1）：32－36.YANG Lufeng，MA Ning，ZHAO Shuangsuo.An adaptive numerical quadrature algorithem of computing with both changeable step and changeable order［J］.Joumal of Yunnan University of Nationalities：Natural Sciences Edition，2011，20（1）：32－36.