基于雙圓弧曲線優化的玻璃切割系統
何發富,張李超
(華中科技大學 材料成形與模具技術國家重點實驗室,湖北 武漢 430074)
1 動機與雙圓弧的定義
1.1 曲線擬合在加工中的重要性
伺服電機與驅動器組成的半閉環控制系統,應用極其廣泛。由于該半閉環控制系統不完全反饋功能會導致加工輪廓局部失真[1]。為滿足加工精度要求,必然要設置額定加工速度、加速度等加工參數來限定加工。傳統數控加工系統采用直線段逼近曲線會造成輪廓曲線的不連續和波動[1],輪廓的局部曲率過大也會導致機床抖動加劇、加工誤差增大等現象發生。因此二維輪廓的平滑處理可以提高加工質量以及增加機床設備工作的平穩性。一些研究者基于尖點、切點、敏感點及可擬合點對曲線進行分段處理,重構優化加工輪廓以消除敏感點對加工質量的負面影響[2]。從實際應用方面來看,G1曲線的路徑可以降低刀具的過切情況、降低高速加工中機床震動及提高產品成形表面質量[3]。本文對分段后的輪廓進行雙圓弧曲線擬合,保證曲線的G1連續性及控制曲線的局部曲率。改善高速加工中不平穩的問題,并滿足曲線拓撲結構不變的要求。
分段圓弧樣條曲線[4]是工程應用的常規方法。本文的目的是使用一系列的圓弧曲線來插補輪廓,并保證圓弧曲線位于指定的容差帶內。這種方法的優點:易保證曲線一階連續、降低原始輪廓微小波動產生的干擾、減少原始輪廓數據量。根據雙圓弧公共點相切的特性,指定曲線通過的節點的切線方向,即可保證擬合的雙圓弧曲線一階連續;當原始輪廓波動的振幅小于容差帶的允許誤差時,干擾波動可以被消除;可以使用較少的雙圓弧曲線擬合輪廓,實現數據壓縮。
1.2 雙圓弧曲線的構造
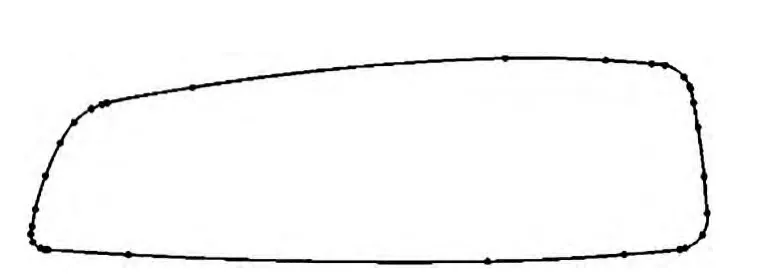
根據Bolton[5]的定義,雙圓弧是一對首尾相連并且連接點切線方向相同的圓弧。楊旭靜[6]對它的幾何計算公式進行了推導。如圖1,平面上任意兩點Ps和Pe以及過這兩點的單位矢量Ts和Te,存在多條首尾分別過Ps和Pe兩點且首尾端單位切矢分別為Ts和Te的雙圓弧,這些雙圓弧形成一個雙圓弧族。圖1所示為雙圓弧族中的一個雙圓弧,Pc為連接點,V為Ps到 Pe的向量,θ1、θ2分別為 V 到 Ts、Te的夾角(順時針方向為正,反之為負),ω1為Ts到PsPc的夾角,ω2為 PcP2到 PcPe的夾角,l=||PsPe||,ρ=||P1Pc||。設 k=||P1Pc||/||P1P2||為 Pc分割 P1P2的比例參數(0 設 ns=PsO1、ne=PeO2,圓心可表示為: 圖1 雙圓弧幾何模型 給定參數條件k,利用上述方程便可以確定雙圓弧方程及相關的幾何數據信息,楊旭靜[6]已經證明參數條件k與圓弧曲線的曲率是單調關系。那可通過k的取值方法不同,找出符合使用者自定義的最優條件的雙圓弧。 根據行業習慣,如果θ1、θ2的符號相同,構造曲線為S型雙圓弧,反之構造C型雙圓弧。 基于容差帶擬合雙圓弧曲線,容差帶直接決定了曲線的擬合精度及拓撲結構。M.Held[7]提出基于輪廓生成的四邊形、扇形、扇盤形組成的k-dops的容差帶算法,它維持曲線的拓撲結構穩定。為消除在輪廓“瓶頸”處容差帶重疊可能會導致曲線自交現象,需要對重疊的k-dops進行緊縮處理,這一處理導致容差帶過渡緊縮及算法性能問題。后來M.Held[8]再提出基于V圖的生成方法計算非對稱的容差帶,這雖然保證了生成的曲線不會發生自相交的情況及在輪廓“瓶頸”處容差帶過渡緊縮現象,但生成V圖復雜性[9]使它不適用于大數據量處理及實時性要求較高的系統;楊旭靜提出基于曲線偏置的局部實時容差帶,但曲線的偏置本身就是一個復雜的過程,加之檢測曲線與曲線的位置關系的復雜性使它存在計算復雜的缺點。本文提出一種快速生成非勻稱的容差帶算法,使輪廓擬合的切線連續雙圓弧曲線位于容差帶內,并對容差帶進行優化處理,解決容差帶過渡緊縮及曲線自相交擬合錯誤的問題。 對給定的平面輪廓(平面多邊形或折線)P,根據M.Held的定義[7],包含P的區域C,如果其邊緣到P的單向 Hausdorff距離 h(p,C)p∈P等于常數 ε,稱 C為P的容差帶,ε為P的容差帶容差。對于折線,其容差帶需要去掉首尾端的半圓形區域。如果一個包含P的條形區域C,其邊緣到P的單向Hausdorff距離 h(p,C)p∈P小于等于常數 ε2大于等于常數 ε1,稱區域 C 為 P 的非勻稱容差帶,區間(ε1,ε2)為 P 的非勻稱容差帶容差,圖2b為圖2a對應的非勻稱容差帶。 圖2 輪廓P容差帶 容差帶的邊緣輪廓由線段和相對較小的圓弧組成,圓弧的數量與線段的數量一致。對計算機來說,圓弧的處理復雜程度是線段的幾倍甚至上百倍,這將消耗很多的計算機資源。本文提出了一種解決方法。稱去掉小圓弧的容差帶為準容差帶,相應的,稱去掉小圓弧的非勻稱容差帶為準非勻稱容差帶,圖2a對應的準非勻稱容差帶如圖2c。大量的實際結果表明,準容差帶與容差帶對雙圓弧曲線的約束效果一致,因此在下文將使用準容差帶來代替容差帶。 定義1:線段端點沿線段法向的偏移距離為線段的端點容差距離εe,線段端點沿端點切線法向上的偏移距離為線段端點法向容差距離εv。輪廓P一般容差帶的線段端點容差距離εe等于容差ε,非均勻容差帶的線段端點容差距離εe與容差區間(ε1,ε2)滿足關系式:ε1≤εe≤ε2。 基于李敏[2]對多邊形或折線輪廓的預處理方法,將輪廓分割為多段可擬合的輪廓段。一段可擬合的輪廓段P,其離散點Pi(i=1,2,…,n),設P的一般容差帶容差為ε,非均勻容差帶的容差ε1=0.5ε、ε2=ε,其非均勻準容差帶的計算方法如下: (1)計算節點Pi的切矢Ti(1≤i≤n)。非封閉的輪廓端點節點切矢使用G.H.Liu[10]的方法構造。取端點及相鄰點 P1、P2、P3,令 A=P2-P1,B=P1-P2,C=A×B,那么 P1的單位切矢T1=D×C/‖D×C‖,其中 D=(‖A‖2(B×C)+‖B‖2(C×A))/2‖C‖2,非端點節點使用平行向量法[11]求其單位切矢; (2)如圖3,預測相鄰節PiPi+1生成雙圓弧的形狀,確定線段PiPi+1的非均勻容差帶的容差帶。已知節點 Pi、Pi+1及曲線切矢 Ti、Ti+1,可預測雙圓弧曲線類型。如果為C型雙圓弧曲線,則緊縮曲線凹側的端點容差距離,如緊縮后的端點容差距離為ε1,凸側端點容差距離不變。如果為S型雙圓弧曲線,則根據切矢與線段的夾角比例系數 k(k=min(|θ1/θ2|,|θ2/θ1|),0 (3)整合所有輪廓線段的容差帶,得到最終的容差帶。對于節點Pi(i=2,3,…,n),其非均勻端點法向容差距離分別在線段Pi-1Pi和線段PiPi+1的容差帶中計算了兩次,由于兩次計算的值不可能完全一致,這必然導致線段Pi-1Pi和線段PiPi+1的容差帶在節點Pi處出現斷裂。為了消除這種斷裂現象,本文將取端點法向容差距離較大的值來重新計算容差帶的坐標,得到輪廓的一個連續非均勻容差帶。 圖3 節點Pi、Pi+1的生成的容差帶d1=ε1<ε2=d2,(ε1,ε2) 為輪廓 P 的非勻稱容差帶容差區間 可擬合的輪廓P,其離散點Pi(i=1,2,…,,n)。取P0Pn進行擬合,如果擬合的雙圓弧曲線包含于輪廓P的容差帶,擬合結束,否則將對P0P(n/2)和 P(n/2)Pn進行擬合,直到擬合成功。如果這個過程中存在某兩相鄰節點PiPi+1(1≤i 圖4 容差帶的整合,取節點處εv較大的值作為目標距離。 如圖5所示,輪廓存在一些所謂“瓶頸”的現象,“瓶頸”處的容差帶出現重合,在曲線擬合時可能會出現曲線自交現象,改變輪廓的拓撲結構,這在工程中是致命的錯誤,這直接使加工件報廢甚至會損壞機床。為了避免這輪廓“瓶頸”處的擬合錯誤,本文將提出一種有效的解決方法。 圖5 容差帶去重疊-擬合曲線與原始輪廓拓撲結構一致 曲線自交的必要條件是容差帶的重疊,那么解決曲線自交的有效辦法就是消除容差帶的重疊現象,也即是對容差帶進行去重疊化處理。簡單而有效的方法就是把重疊區域從中間分割,這樣容差帶永遠只可能相接而不會重合,根據擬合中曲線必須在容差帶內的這一條件,保證了擬合后的曲線不會發生自相交的情況。如圖6a是去容差帶去重疊化后的擬合結果。 本文提出的基于輪廓非均勻容差帶的雙圓弧擬合算法,已經實現并集成到玻璃切割系統的二維輪廓優化處理模塊中,在南京燁拓自動化設備有限公司的自動化球面玻璃切割設備中成功應用。使設備的加工速度由原來的6.5m/min提高到10m/min,加工面的粗糙度也明顯得到改善。 圖6 容差帶去重疊-擬合曲線與原始輪廓拓撲結構一致 由于水刀玻璃切割適合厚板慢速切割[12],常規玻璃都采用金剛石刀頭進行切割。由于玻璃易碎、硬度高等特性,決定了其加工過程中不能有太大的震動,否則刀具容易被損壞,同時加工面將很粗糙甚至產品報廢;再者,刀具與毛坯表面的接觸力要均勻且適中,接觸力過小會導致割痕淺,以至后續加工失敗,接觸力過大產生的深割痕難以在后續加工中去除,影響加工質量。由此,為減小報廢率,玻璃切割設備必須運行平穩,切割輪廓路徑需平滑。 為了達到輪廓平滑的要求及設計方便,玻璃切割輪廓一般由直線、圓弧及Nurbs樣條曲線組成。在玻璃切割領域,輪廓基本是根據需要反求而來,這個過程容易導致輪廓在曲線與曲線的連接處切線微小的不連續,極大的限制了加工速度及加劇了機床的震動,這就需要在后續進行平滑重構處理。 目前數控系統不支持Nurbs樣條曲線,通常的方法是使用線段來插補樣條。本文采用線段來插補輪廓,然后再使用雙圓弧來擬合線段輪廓,由于擬合后的雙圓弧曲線G1連續,即可實現重構后的輪廓平滑。圖7展示了重構后局部輪廓的平滑效果,圖7a中圓圈處輪廓存在微小的不連續,這些不連續很微小,重構后的曲線在鏈接處切線連續,實現消除原始輪廓微小切線不連續的缺陷。 圖7 重構消除了原始輪廓的不平滑 重構的另一個方面可以大大的減少輪廓的數據量,原始的方法是使用短線段及圓弧來標示輪廓,從局部上來看,在誤差允許范圍內,多條線段可以使用一個圓弧來表示,使用雙圓弧重構的方法是可以極大限度的使用最少的圓弧數量來表示原始輪廓,實現數據壓縮。圖8所示輪廓的原始線段和圓弧的數量為554,重構后的圓弧數量為31,圖中輪廓上的小黑點為圓弧與圓弧之間的連接點。大量的實驗室數據表明重構對原始輪廓的數據壓縮比例約為1%~20%。 圖8 重構后圓弧數量大大減少 重構的穩定性也可以通過容差帶的去重疊化處理得到保證。重構后的輪廓的拓撲結構保持與原始輪廓的拓撲結構一致,保證重構后的在輪廓“瓶頸”處不會發生自相交情況。容差帶在輪廓“瓶頸”處發生重疊,擬合的曲線雖然都在輪廓對應的容差帶內,但不能保證曲線在容差帶的重疊區域放生自交,改變輪廓的拓撲結構。實驗結果證明算法可以有效的把重疊區域相對平均的分配給競爭區域,實現容差帶相鄰而不重疊,保證擬合曲線不會出現自交擬合錯誤,保證擬合曲線與原始輪廓拓撲結構一致。 對有n個離散節點的輪廓,算法計算節點切矢、準非勻稱的容差帶的時間復雜度分別為O(n)、O(2n)。假設相鄰節點的雙圓弧曲線都在容差帶內,最壞情況下,算法擬合曲線的時間復雜度為O(log2n),總時間復雜度為O(log2n+3n)。表1顯示了算法在擬合曲線的各個階段的時間消耗,從表中數據顯示,算法的復雜度為線性的,對處理數據量比較大的輪廓也非常快,重構不會成為系統處理輪廓的瓶頸。 表1 時間消耗 表中時間時間t(單位為ms),擬合n個節點輪廓的雙圓弧曲線,輪廓的容差帶容差為(0.05,0.1)。合計的時間包括了輪廓節點的前期處理。實驗平臺:Windows NT系統,intel 1.7GHz處理器,4GB內存。 經使用雙圓弧擬合技術進行平滑重構后的2D輪廓,投影到球面上的三維加工路徑依然是一階連續的。應用平滑處理技術后,原來的玻璃切割設備的加工效率得到大大的提高,在沒有使用雙圓弧擬合技術前,當加工速度超過6.5m/min時,機床會發生明顯的震動及加工質量下降問題,使用雙圓弧擬合技術平滑處理輪廓后,加工速度可以提高到10m/min,加工質量也明顯得到改善,圖9展示使用雙圓弧擬合技術前后的加工件質量。 圖9 雙圓弧擬合平滑處理,改善加工質量 本文針對伺服控制器加電機的半閉環控制加工設備,為解決存在的運動不平穩、加工質量粗糙問題,提出并實現了一種對二維輪廓重構優化的平滑處理技術。采用一種基于輪廓容差帶控制曲線擬合誤差的雙圓弧擬合算法對可擬合輪廓段進行平滑處理,并滿足擬合曲線與原始輪廓拓撲結構一致,有效的控制曲線擬合誤差,實現了加工輪廓的G1連續。通過加工對比試驗發現:二維輪廓經平滑處理后,加工效率顯著提高,零件質量顯著改善,輪廓更加光順,誤差更小,很好地解決了機床抖動頻繁影響運動平穩性的問題,驗證了本文提出的平滑處理算法是合理可行的。 [1]王海濤,趙東標,高素美.參數曲線的自適應實時前瞻插補算法[J].計算機集成制造系統,2010,16(2):385-389. [2]李 敏,張李超,莫健華.一種數控加工二維輪廓的平滑處理技術[J].計算機集成制造系統,2011,12(17). [3]劉愛林.片材疊層制造中若干關鍵技術的研究[D].武漢:華中科技大學,1999. [4]楊雨牲,趙曉東.一種簡便的圓弧樣條曲線擬合方法及計算[J].鍛壓機械,1996,2:51-52. [5]Bolton KM.Biarc curves[J].Computer Aided Design,1975,7(2):89-92. [6]楊旭靜.自由曲面高性能數控加工刀具路徑技術研究[D].湖南大學博士學位論文,2006. [7]M.Held,J.Eibl.Biarc approximation of polygons within asymmetric tolerance bands[J].Computer Aided Design,2005,37(4):357-371. [8]M.Heimlich,M.Held.Biarc approximation,simplification and smoothing of polygonal curves by means of Voronoi-based tolerance bands[J].International Journal of Computational Geometry and Applications,2008,18(3):221-250. [9]Oswin Aichholzer,Wolfgang Aigner.Divide-and-conquer for Voronoi diagrams revisited[J].Computational Geometry,2010,43:688-699. [10]G.H.Liu,Y.S.Wong,Y.F.Zhang,H.T.Loh.Adaptive fairing of digitized point data with discrete curvature.Computer-Aided Design,2001,34:309-320. [11]張三元,伍家鳳,梁友棟.3D數據點列的雙圓弧樣條插值[J].浙江大學學報(理學版),2000,27(5):540-543. [12]溫效康,宋擁政,梁志強.高壓水切割技術的試驗研究[J].鍛壓機械,1994,29(5):15-19.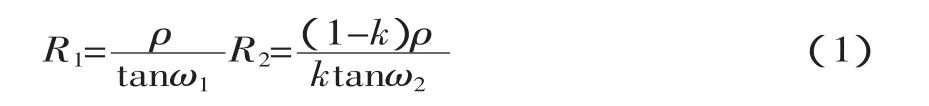
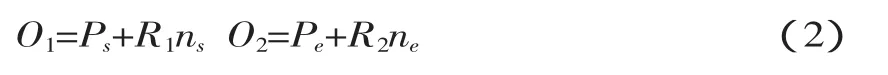
1.3 雙圓弧擬合算法的發展
2 雙圓弧擬合算法的實現
2.1 非勻稱容差帶的定義

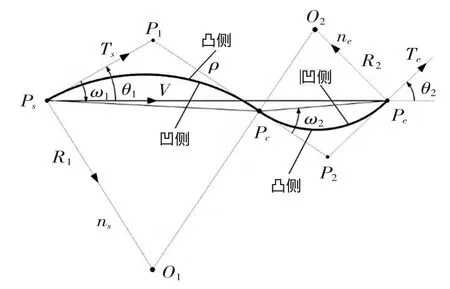
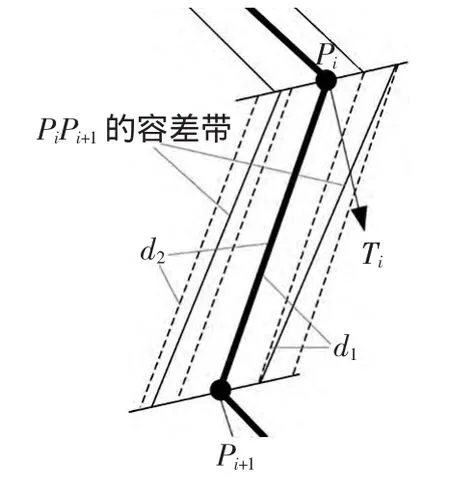
2.2 非均勻準容差帶的生成
2.3 雙圓弧曲線擬合

2.4 容差帶的優化

3 在玻璃切割系統中的應用

3.1 玻璃切割設備及加工輪廓要求
3.2 輪廓的平滑化重構


3.3 加工質量

4 結束語

