功率放大器及預失真器模型的設計

王 偉，曹 民，朱娟娟，王 戈，李 龍

0 引言

隨著移動通信市場的迅速發展，對移動通信技術提出了更高的要求。有限的可用頻譜資源遏制了現代通信系統的發展。為了通信事業更好地發展，必須提高頻譜利用率。

在通信系統中，功率放大器是造成系統非線性的主要來源。當發射信號的功率增加到一定程度時，會使信號進入非線性區域，從而造成頻譜拓寬、帶內頻譜失真。因此，功率放大器的線性化可以抑制頻譜泄露、鄰道干擾以及減小誤比特率［1］。

為了克服上述缺點，在所有線性化技術中，數字預失真技術是補償功率放大器最有效、最有前景的功放線性化技術之一。

1 數學模型

冪級數模型和多項式模型被廣泛用于描述功率放大器的非線性效應。文中主要介紹正交多項式模型。根據函數逼近Weierstrass定理［2］，可以用一個階數充分大的多項式去逼近功放到任意程度，故可采用正交多項式表示功放的非線性函數。

1． 1 建模原理

信號的功率放大是通信系統的關鍵功能之一，其實現模塊稱為功率放大器。功放的基本原理是:輸入信號通過功率放大器輸出較大功率的信號。預失真器的基本原理是:在功放前設置一個補償器，它具有功放的逆特征，用來彌補功放的非線性。這兩個模塊的合成效果使得整體輸入－輸出特性線性化，輸出功率得到充分利用。系統原理如圖1所示。

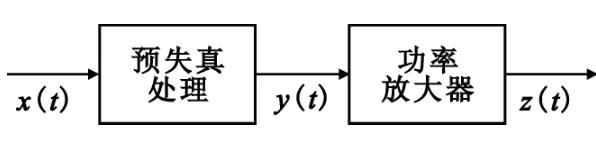
圖1 系統原理Fig．1 Principle diagram of the system

設功放輸入－輸出傳輸特性為G()，預失真器特性為F()，系統處理原理可表示為:

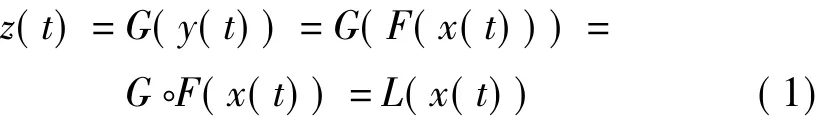
G?F=L表示為G()和 F()的復合函數等于L()。線性化則要求:

式中，常數g是功放的理想“幅度放大倍數。因此，當功放特性G()已知，則預失真技術的核心是尋找預失真器的特性F()，使得它們復合后能滿足:

如果測得功放的輸入和輸出信號值，就能擬合功放的特性函數G()，然后利用式(3)，可以求得F()。

1． 2 傳統多項式模型

在實際運算中，功放輸入y(t)、輸出z(t)，進行離散采樣后值為分別為y(n)、z(n)(采樣過程符合Nyquist采樣定理要求)，功放模型分為無記憶和有記憶模型兩種。傳統多項式表示為:

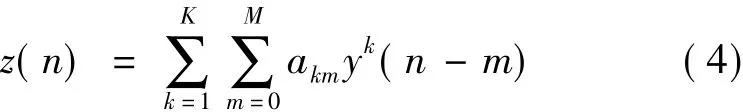
由于常用復值輸入－輸出信號，式(4)可化為“和記憶多項式”模型:

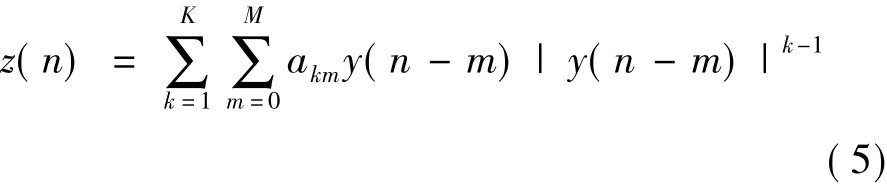
式中，M表示記憶深度，當M等于0時，該形式化簡為無記憶功放模型，M不等于0時，該式展開為有記憶功放模型，n 的范圍為 n=0，1，2，…，N，akm為功率放大器模型的參數。

預失真器的模型仍為正交多項式模型，其模型為式(5)。

當線性化系統的輸出為z(n)時，則系統輸入為z(n)/g，即預失真器的輸入，而功放的輸入為x(n)，即預失真器的輸出。所以將預失真器的輸入為z(n)/g，輸出為x(n)，代入式(5)可得到預失真器的模型:

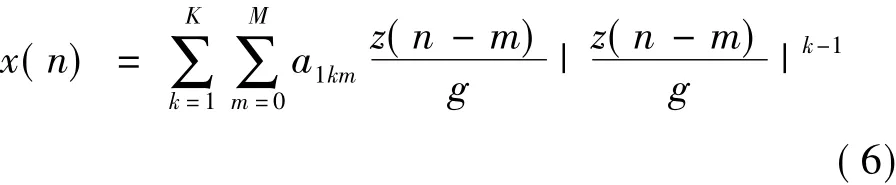
式中，a1km為預失真器模型的參數，g是功放的理想幅度放大倍數。

將原始數據x(n)帶入預失真器模型式(5)，輸出得到y1(n)，再將y1(n)帶入功放模型式(6)中，輸出得到z1(n)。

1． 3 正交多項式模型

功放模型用正交多項式可表示為:

用線性最小二乘法求系數矩陣h:

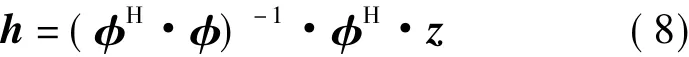
對于無記憶正交多項式:

h表示

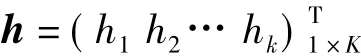
φ表示

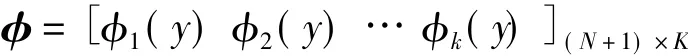
φk(y)表示

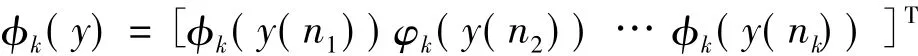
φk(y(n))表示

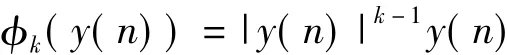
對于有記憶正交多項式［3］:

h表示

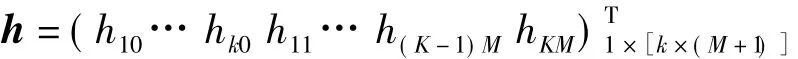
φ表示

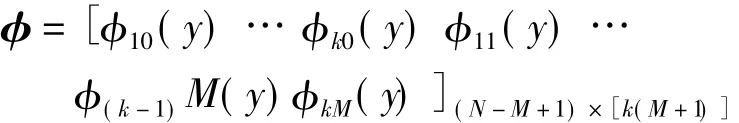
φkm(y)表示

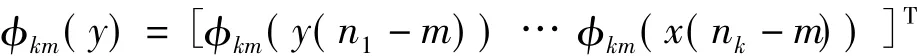
φkm(x(n－m))表示

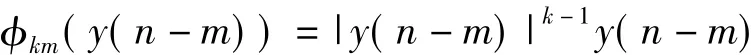
求解步驟同上:先求出功放的系數矩陣，再求出預失真器的系數矩陣。將原始數據x(n)帶入預失真器模型，輸出得到y2(n)，在將y2(n)帶入功放模型中，輸出得到z2(n)。

1． 4 評價模型指標

以上模型的數值計算結果常用NMSE和EVM評價整體模型，如下:

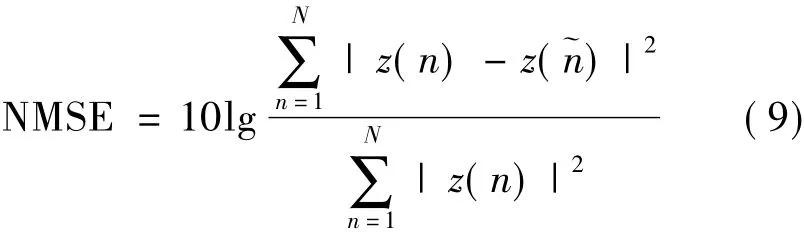
采用歸一化均方誤差 (NMSE)來表征計算精度，如果用z表示實際信號值，?z表示通過模型計算的信號值，NMSE就反映了模型與物理實際模塊的接近程度。

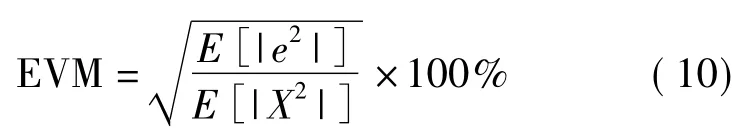
誤差矢量幅度(EVM)定義為誤差矢量信號平均功率的均方根和參照信號平均功率的均方根的比值。如果用x表示理想的信號輸出值，e表示理想輸出與整體模型輸出信號的誤差，那么EVM衡量整體模型對信號的幅度失真程度。

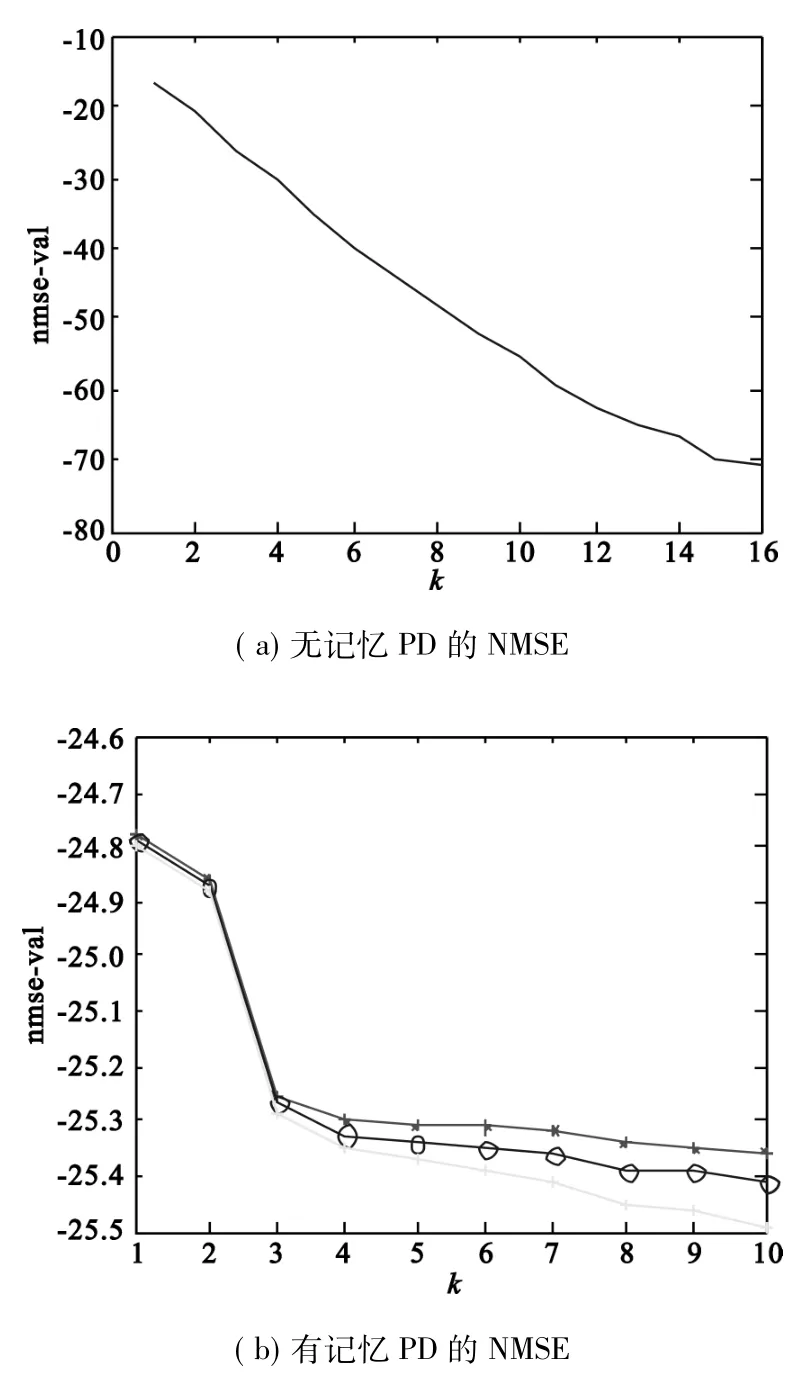
圖3 無記憶和有記憶預失真模型的評價指標Fig．3 Evaluation index figure of predistorter models with memory and without memory

2 模型求解

2． 1 正交多項式模型評價指標

系統分為無記憶模型和有記憶模型，評價結果如圖2和圖3所示。

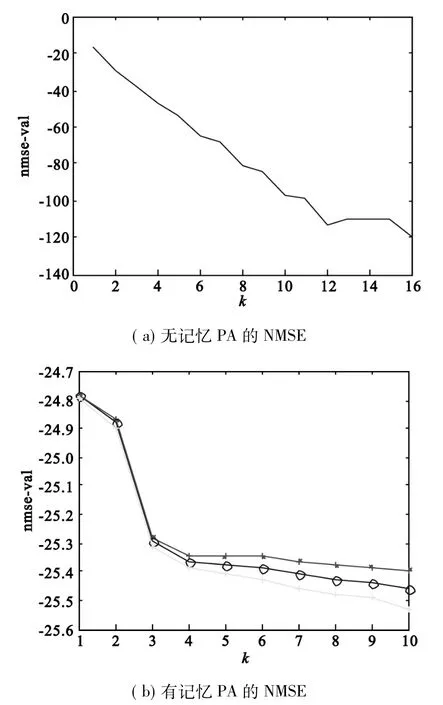
圖2 無記憶和有記憶功放模型的評價指標Fig．2 Evaluation index figure of the power amplifier models with memory and without memory

圖2 (a)、圖3(a)分別為無記憶功放模型以及預失真模型的NMSE圖，可知道，無記憶模型的階數由0遞增到16的過程中，NMSE的取值隨著階數的提高迅速降低，客觀的反映了正交多項式的階數在無記憶模型與物理實際模塊之間的逼近程度。圖2(b)、圖3(b)分別為有記憶功放模型以及預失真模型的NMSE圖，可知道，有記憶模型的階數由0遞增到10過程中，NMSE的取值隨著階數的提高迅速降低，且記憶深度由1遞增到3的過程中，NMSE的取值也會降低，客觀的反映了正交多項式的階數和記憶深度在有記憶模型與物理實際模塊之間的逼近程度。

2． 2 正交多項式仿真結果

系統分為無記憶模型和有記憶模型，仿真結果如圖4和圖5所示。

圖4為階次K=5經過預失真器的無記憶功放模型仿真圖，EVM=1．4%;圖5為階次 K=5、記憶深度M=2經過預失真器的有記憶功放模型仿真圖，EVM=0．55%，可知道，經過前置預失真器的功放模型，使得整體輸入、輸出特性滿足線性化關系;客觀的衡量無記憶和有記憶模型對信號的幅度失真程度。

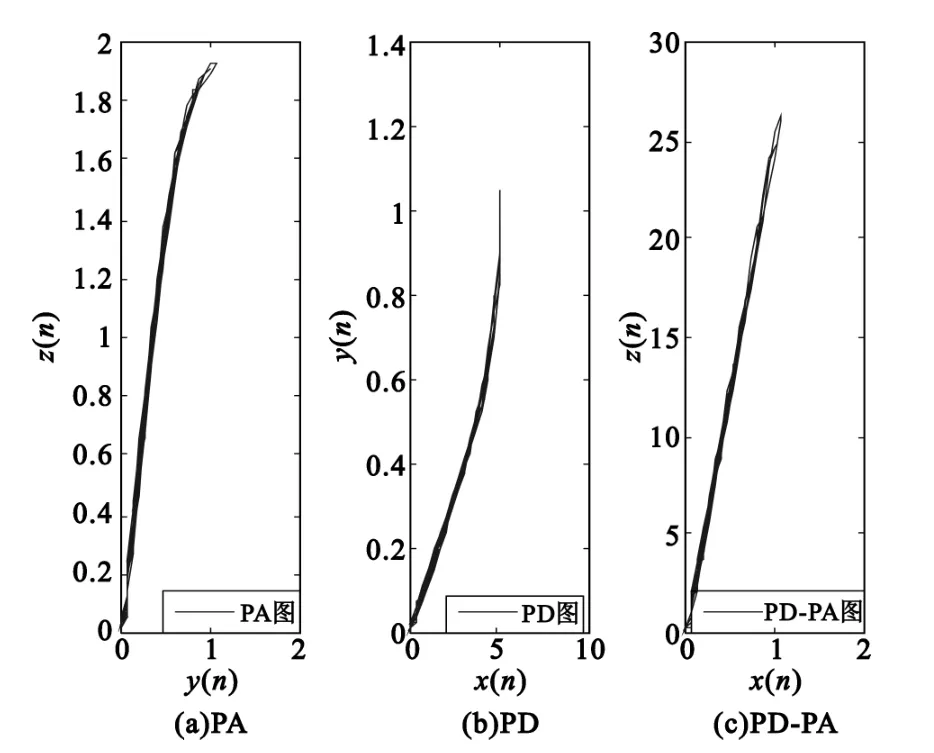
圖4 無記憶模型Fig．4 Models without memory

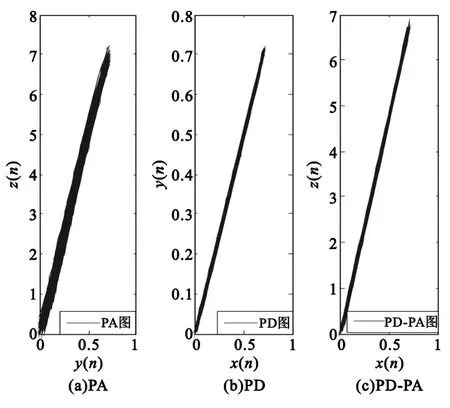
圖5 有記憶模型Fig．5 Models with memory

2． 3 正交多項式模型的特點

傳統多項式從原理考慮n取越大越好，但由于數據量的限制，MATLAB軟件調用polyfit函數無法求出所需高階多項式的全部參數，且高階時會引起數值的不穩定;文中引用了正交多項式模型，該方法在求取高階多項式參數時不受樣本數據量的限制，減輕了數值不穩定的問題，建立高精度的功率放大器和預失真器模型，進而改善系統的指標。

3 結語

文中針對無記憶功放和有記憶功放分別建立了預失真模型，其中利用功放的實際輸入輸出樣本數據求取預失真器模型的方法較為巧妙，并最終采用誤差矢量幅度對所建模型進行了評價，結果表明，文中所建立的模型的輸出值與理想輸出值有較好的近似程度，且對信號的幅度有一定程度的改善。

［1］ 胡莉莉，艾渤．功率放大器記憶效應分析及有記憶預失真技術［J］．通信技術，2011，44(05):45 －77．

HU Li－ li，AI Bo．Memory Effect Analysis of Power Amplifier and Predistorter Technology［J］．Communications Technology，2011，44(05):45－77．

［2］ RAVIV R，QIAN Hua，ZHOU Tong．Orthogonal Polynomials for Power Amplifier Modeling and Predistorter Design［J］．IEEE Trans．Vehicular Technology，2004，53(05):1468－1479．

［3］ ZHOU G T，KENNEY J S．Predicting Spectral Regrowth of Nonlinearpower Amplifiers［J］．IEEE Trans．，2002(50):718－722．