Some special solvable subgroups of SL(n,C) and their application
(Mathematics Department, Tianhua College of Shanghai Normal University, Shanghai 201815, China)
Some special solvable subgroups ofSL(n,C) and their application
FUChunhong
(Mathematics Department, Tianhua College of Shanghai Normal University, Shanghai 201815, China)
It is well known that Fuchsian equations have widespread and important application in mathematical physics problems. Therefore the research on the judgment of integrability for some given Fuchsian equations has significance both in theory and application. By Khovanskiy theorem, the problem on judging the integrability of Fuchsian equations can be changed into deducing the corresponding monodromy groups and checking their solvability. But as the theory is still imperfect, up to now, no effective method has been introduced to resolve this problem for a certain Fuchsian equation. In this paper, the author gives several classes of special solvable subgroups inSL(n,C), and their application for Fuchsian systems. By the relation between the solvability of monodromy group and the integrability of Fuchsian equations, the conclusion is if solution of Riemann surface of Fuchsian system is a surface of two dimensional bounded closed mainfold with getting rid of poles, where the number of poles is finite, then monodromy group of this system must be finite and linear. Especially, if generated elements satisfy the condition of the theorems in the paper, the monodromy group must be solvable. Thus the system is integral in quadratures.
integrability; Fuchsian equation; monodromy group; solvable group; special linear group
It is well known that Fuchsian equations have widespread and the important application in the mathematical physics problems. Therefore the research on the judgment of integrability for some given Fuchsian equations has significance both in theory and application. By Khovanskiy theorem[1], the problem on judging the integrability of Fuchsian equations can be changed into deducing the corresponding monodromy groups and checking their solvability. But as the theory is still imperfect, up to now, no effective method has been introduced to resolve this problem for a certain Fuchsian equation.
Article[2-4] discussed the structure of solvable subgroup ofSL(2,C) and a class ofSL(3,C), and integrability of Fuchsian equations on torusT2. In this paper, we will introduce some subgroups ofSL(n,C) and obtain several classes of solvable subgroups, then we apply them into Fuchsian system.
1Themainresults
LetCis the complex field.SL(n,C) isn-order special linear group inC, i.e.
SL(n,C)={A∈Cm×n|detA=1}
Let
ObviouslyKis a subgroup ofSL(n,C). Assume that elementAandBbelong toK. LetG=〈A,B〉, and is a subgroup ofSL(n,C) that generated byAandB. The main theorems are as follows:
Theorem1 LetG=〈A,B〉 is a subgroup ofSL(n,C), thenGis a solvable group if and only ifAandBbelong to one of the following cases:
1)AandBmay be simultaneously similar to upper (lower) triangular matrix.
2) There exists a nonsingular matrixP, such that
Theorem2 LetA1,A2,…,Al∈SL(n,C),l∈N
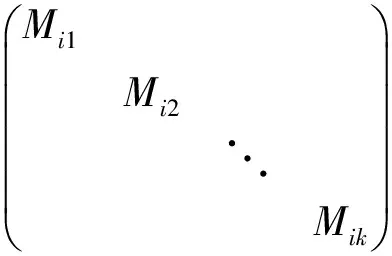

whereMis∈H,1≤i≤l,1≤s≤k.
ThenG=〈A1,A2,…,Al〉is a solvable group.
2Lemmasandproofofthemaintheorems
Lemma2[6]LetT(n,C) is a group of all upper triangular matrices ofGL(n,C). ThenT(n,C) is solvable.
Lemma3[6]LetGis a non-cyclic free group, thenG′ is a free group with infinite rank (G′ is the derived group ofG).
Lemma4 Each element ofKmay be unique expressed by one of the following two forms:
or
It is easy to verify this proposition is true by Bruhat Decomposition theorem[7]
Lemma5AandBmay be simultaneously similar to upper(lower) triangular matrices if and only if there is a same eigenvectors of 2-order sequential principal submatrix ofAandB.
In fact, obviously the necessity is right. The next step we will verify the sufficiency is true. Let 2-order sequential sub-matrices ofAandBareA2,B2. Assume there is a same eigenvector.
By ref[2], there exists a nonsingular matrixP2∈GL(n,C) such that
Proofoftheorem1 We divided the problem into three cases:
1) IfAandBare simultaneously similar to upper(lower) triangular matrix. By lemma 1,2,G=〈A,B〉 is solvable.
IfAandBare different from case 1). Without loss of generality, by lemma 4 we may let
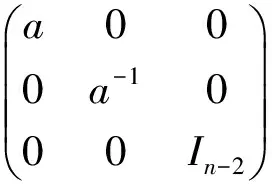
Since〈A,B〉={An1Bm1An2Bm2…AnkBmk|ni,mi∈Z,i∈N}, by (1) we can conclude
〈A,B〉={AnBm|n,m∈Z}
and 〈A,B〉′≤〈A〉. Since 〈A〉 is a cyclic group, thereforeG″≤〈A〉′=In. Thus result is effective.
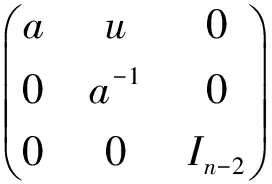
Therefore by (2)
LetG1=〈A,A1〉=〈A,BAB-1〉. ThenG1is a normal subgroup ofGandG/G1=〈A,B〉/〈A,A1〉?{Bm|m∈Z} SinceB4=In, so
G/G1?{In,B,B2,B3}

and
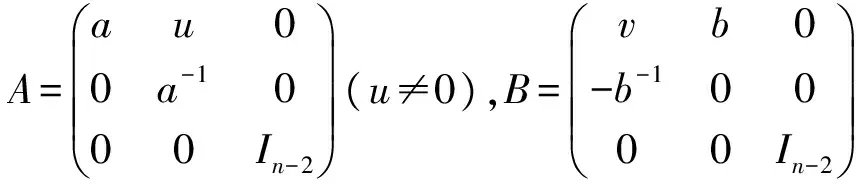
By case 3), we can easy to verifyG=〈A,B〉is not solvable. So letG=〈A,B〉 is solvable if and only if one of the two cases of theorem 1 takes place. Until now, the proof is completed.
Lastly, it’s not difficult for us to prove theorem 2 by operational properties of partitioned matrix and main results in ref[2].
3SolvabilityofmonodromygroupandintegrabilityofFuchsianequations
Generally, letn-order Fuchsian system as follows:
whereρi(z)(1≤i≤n) is meromorphic function.
By Khovanskiy theorem, if monodromy group of solutions has a solvable normal divisor of finite index, then eq.(*) must be integral in quadratures. This means that the solution of the system can be expressed in terms of the coefficient functions by solving algebraic equations, integrations and compositions with entire functions by several times.
We know that orientable two-dimensional closed mainfolds include spherical surface, torus, double torus, many torus and so on, and linear representation groups of homotopy groups are finite generated linear groups on that. So we obtain theorem 3 as follows:
Theorem3 If solution of Riemann surface of Fuchsian system is a surface of two dimensional bounded closed mainfold with getting rid of poles, where the number of poles is finite, then monodromy group of this system must be finite and linear. Especially, if generated elements satisfy the condition of theorem 1 or theorem 2, the monodromy group must be solvable. Thus the system is integral in quadratures.
[ 1 ]ANOSOV D V, AMOLD V I. Dynamical Systems I[M]. Berlin:Spring-Verlag, 1985:50-245.
[ 2 ]ZHANG Shaofei, GUAN Keying. Structure of solvable subgroup ofSL(2,C) generated by two elements and its application in Fuchsian equations[J]. Mathematical Research and Exposition, 1999,19(4):704-708.
[ 3 ]GUAN Keying, ZHANG Shaofei. Structure of sovable subgroup ofSL(2,C) and integrability of Fuchsian equations on torus[J]. Science In China: Series A, 1996,26(3):221-225.
[ 4 ]ZHANG Shaofei, FU Chunhong. The structure of a class of solvable subgroups ofSL(3,C) and integrability of Fuchsian equations[J]. Pure and Applied Mathematics, 2008,24(4):625-630.
[ 5 ]ZHANG Yuanda. Structure of finite groups (Book 1)[M]. Beijing: Chinese Science and Technique Press, 1982:126-456.
[ 6 ]DEREK J R. A Course in the theory of groups[J]. New York: Springer-Verlag,1982.
[ 7 ]SERGEL L.SL(2,R)[M].NewYork: Springer-Verlag, 1985.
[ 8 ]FUCHS J L. Zur Theorie der linearen differentialgleichungen mit Ver?nderlichen Koeffizienten[J]. Reine Angew Math, 1866,66(2):121-160.
[ 9 ]LAPPO I A. Applications des fonctions matrices dans la theorie des systèeme des équations différentielles ordinaires lineaires[M]. Moscow: Addison-Wesley,1957.
[10]CHUDNOVSKY D V. Riemann, monodromy problem, isomonodromy deformations and completely integrable systems[J]. Bifurcation Phenomena in Mathematical Physics and Related Topics, 1980:385-447.
[11]JIMBO M, MIWA T, SATO M. Holonomic quantum fields-the unanticipated link between deformation theory of differential equations and quantum fields[J]. Mathematical Problems in Theoretical Physics, 1980:119-142.
[12]BIRKHOFF G D. A simplified treatment of the regular singular point[J]. Mer Math Soc, 1910,11(2):199-202.
[13]CODDINGTON E A, LEVINSON N. Theory of ordinary differential equations[M]. New York: McGraw-Hill, 1955:258-562.
[14]POINCARE H. Papers on Fuchsian functions[M]. New York: Springer, 1985.
[15]FARKAS H M, KRA I. Riemann Surfaces[M]. New York : Springer-Verlag, 1980.
[16]MARDEN A, RICHARDS I, RODIN B. Analytic self-mapping on Riemann surfaces[J]. D Analyse Math, 1967,18(1): 97-225.
[17]高振興. 矩陣的分塊與應(yīng)用[J]. 遼寧師范大學(xué)學(xué)報(bào):自然科學(xué)版, 2010,33(3):305-310.
[18]張秀偉. 矩陣的Γ-(i,…,j)逆[J]. 遼寧師范大學(xué)學(xué)報(bào):自然科學(xué)版, 2011,34(2):157-160.
1673-5862(2014)04-0529-04
SL(n,C)中的一些特殊可解子群及應(yīng)用
付 春 紅
(上海師范大學(xué)天華學(xué)院 數(shù)學(xué)教研室, 上海 201815)
Fuchs方程在許多物理問(wèn)題中有著廣泛而重要的應(yīng)用,所以判定給定的Fuchs方程的可積性及解的性質(zhì)在理論與應(yīng)用中都有意義。根據(jù)Khovanskiy定理,Fuchs方程的可積性判定問(wèn)題可轉(zhuǎn)化為對(duì)其單值群的計(jì)算并判斷其可解性,但由于這方面理論及計(jì)算的發(fā)展尚不完善。到目前為止,對(duì)任意給定的Fuchs方程,并不存在行之有效的方法求出單值群以及判斷其可解性。給出了SL(n;C)中的幾類(lèi)特殊可解子群,并應(yīng)用于Fuchs系統(tǒng).由Fuchs方程的單值群的可解性與其可積性的關(guān)系,得出結(jié)論,若Fuchs系統(tǒng)解的Riemann曲面是二維有界閉流形上除去有限個(gè)極點(diǎn)的曲面,則其單值群必然是有限生成的線性群。特別若生成元滿足本文所列之條件,則單值群必可解,從而Fuchs方程可積。
可積性; Fuchs方程; 單值群; 可解群; 特殊線性群
date: 2014-02-16.
O151Documentcode: A
10.3969/ j.issn.1673-5862.2014.04.015
Supported: Project supported by the National Natural Science Foundation of China (19671009).
Biography: FU Chunhong(1980-),female, lecturer of Tianhua College of Shanghai Normal University, master degree.

