SIFT算法研究內容概述

袁榮慶，謝勁松

(長春理工大學 機電工程學院，長春 130022)

0 引言

尺度不變特征變換(Scale Invariant Feature Transform)-簡稱SIFT算法是由就職于英屬哥倫比亞大學主攻機器視覺方向的David Lowe提出的，該算法首先要尋找尺度空間中的極值點，通過提取局部特征來提取算法。我們研究的SIFT算法主要由以下四步組成。

1 尺度空間極值點檢測

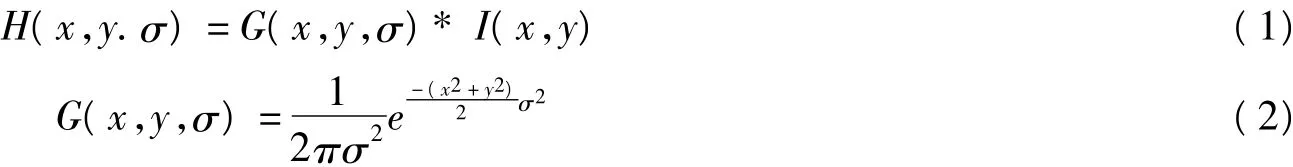
其中G(x，y，σ)是尺度可變高斯函數，(x，y)表示圖像像素點位置，σ表示空間因子，由上式得到的值越小表示圖像的尺度越小。

SIFT算法第一步就是要獲得尺度空間的極值點，為了能有效的檢測到關鍵點，我們提出了高斯差分尺度空間這一概念。下式是高斯差分函數。

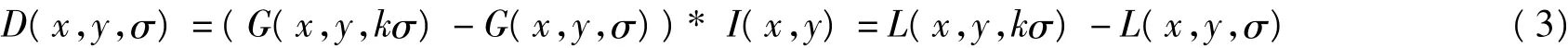
高斯差分函數相比于其他的函數在極值點檢測中有著較高的計算效率，并且和尺度歸一化的拉普拉斯高斯函數σ2?2G有近似的關系，另外計算相比其他算子也較為簡單。

圖像金字塔的構建:理論上圖像金字塔共有O組，每組的圖像層數有S層。圖1表示了兩組圖像金字塔，它們都是通過高斯差分尺度空間建立起來了，如圖1中箭頭所示，第二組最底層圖像由第一組第一幅到最后一幅圖像降采樣得到。圖2為DOG算子的構建示意圖，兩個相鄰區間的差異在高斯金字塔創建一個間隔difference-of-Gaussian金字塔所示。

在構造圖像金字塔的過程中，首要是建立圖像金字塔的第一層。金字塔的第一層都是由被檢測圖像進行高斯卷積之后得到的該圖像的不同尺度空間。對第一層第一幅圖像進行兩倍尺度兩倍像素距離下采樣得到圖像金子塔中第二層的第一幅圖像，并以該圖像為基準做高斯卷積，得到第二層的全部圖像。同樣的道理，第三層的第一幅圖像也是由第二層第一幅圖像以兩倍尺度兩倍像素距離降采樣得到的，之后通過對第三層第一幅圖像進行高斯卷積得到該層的全部圖像。以此類推，可以得到用高斯差分函數處理過得全部圖像，并呈現出金字塔形狀。其過程用圖3表示。

尺度空間的理論目的是模擬圖像的多尺度特征。采集到的特征點的圖像特征必須保持尺度不變性，并且在多尺度空間內完成，其中較為典型的是高斯卷積。高斯卷積能很好的實現尺度變換，也能很好的進行線性變換。我們用下式定義一幅二維圖像的尺度空間:

圖1 圖像金字塔構建

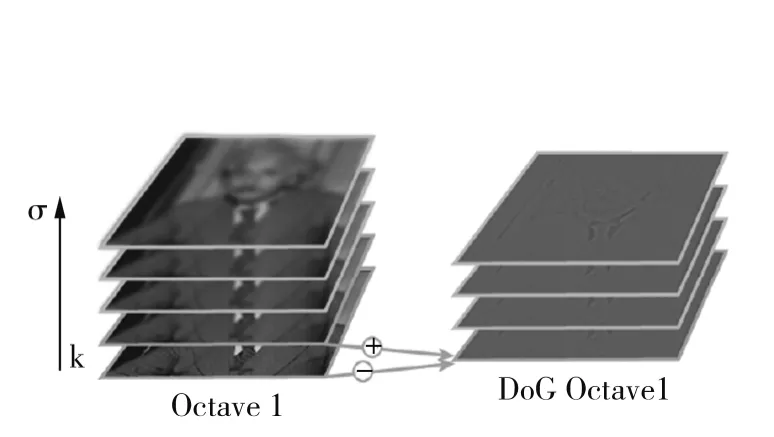
圖2 DOG算子構建示意圖

圖3 獲取DOG尺度空間圖像示意圖

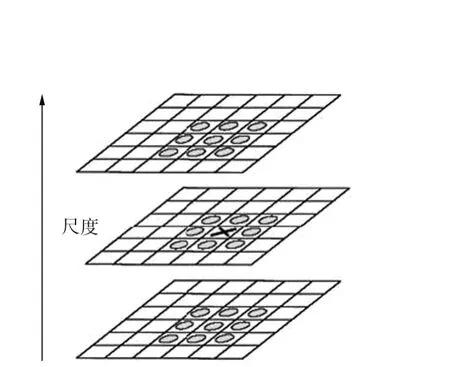
圖4 DOG尺度空間局部極值檢測

在DOG尺度空間中，為了尋找到極值點，需要將每一個待檢測點和周圍相鄰圖像域、尺度域的點進行大小比較，確保檢測準確性。如圖4所示，中間尺度域中叉號表示待檢測點，為了保持檢測準確性，它需要和圍繞在周圍的同尺度域的8個點進行比較，還要和相鄰兩個尺度域中同樣位置的上下各9個點進行比較，確保在DOG尺度空間極值檢測中檢測到合適的極值點。

2 精確確定極值點位置

在通過建立高斯圖像和高斯差分圖像找到極值點之后，我們下面需要精確極值點的位置。由于DOG算子本身就有提高圖像抗噪聲的能力，圖像會有較強的邊緣響應，為去除這些不穩定的極值點和邊緣響應點，我們用擬合二次函數來去除不穩定的極值點和邊緣響應點。用泰勒公式將該函數在極值點處展開，

X=(x，y，σ)T表示極值點在圖像中的偏移量，D表示DOG(X)極值點處的值。

3 確定關鍵點的主方向

在使用高斯圖像局部極值檢測確定了極值點之后，我們需要找到局部結構的穩定方向，這是為了實現圖像在旋轉時不變性。由前面求得的極值點的尺度值，我們可以據此得到和該尺度值接近的高斯圖像。

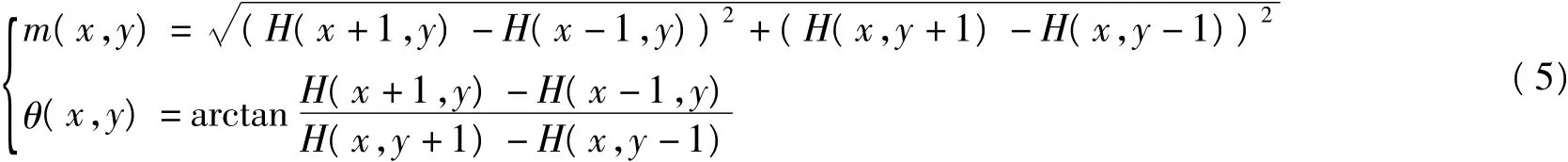
每個檢測到的極值點我們所在的尺度空間我們用H來表示。確定極值點處的梯度大小和方向公式之后，下面是確定極值點方向的方法，這里我們常用的是直方圖統計法。

(5)式中，m(x，y)和θ(x，y)分別為高斯金字塔(x，y)處梯度的大小和方向，H所用到的尺度為每個關鍵點所在的尺度。確定關鍵點的方向采用梯度直方圖統計法，建立如圖5所示的梯度直方圖，檢測到的極值點作為原點，極值點相鄰區域內的像素點通過比較結合梯度方向的大小，確定極值點的主方向。所選區域為以極值點為原點的0-360°的圓形區域內，理論上要以每10°作為一個節點建立36個直方圖，在直方圖中具有最大峰值的代表了極值點的主方向。

就此，我們極值點檢測完畢，得到了圖像中極值點的尺度空間大小、極值點主方向和極值點的位置信息。

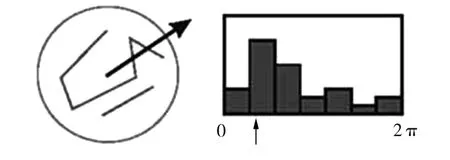
圖5 由梯度方向直方圖確定主梯度方向

4 關鍵點的描述

在確定了關鍵點之后，為了計算上的方便，我們需要用向量的形式將關鍵點表征出來，描述的信息不僅要包括關鍵點的信息也要包括關鍵點周圍的其他像素點信息，該向量具有唯一性，我們稱之為SIFT描述子。具體方法是首先將關鍵點周圍的圖像分塊，然后和我們在確定關鍵點主梯度方向時一樣，在分塊的區域內建立梯度直方圖，從而確定該區域內的獨特向量。

圖6表示一個SIFT描述子實例。圖中中心點表示的是確定的關鍵點，左圖中的每一個小方格表示關鍵點周圍的鄰域尺度空間內的一個像素，方格內箭頭的長短和方向分別表示了該像素點的梯度值大小和方向。以關鍵點為原點的360°方向內尋找鄰域內的像素點并將每8×8方格內的像素點建立如右圖所示的特征向量圖。我們可以看到，每8×8的方格內像素點能夠累加成為一個種子點，而一個關鍵點要包括4個這樣的種子點信息。這種方法雖然復雜，但是能很好的結合關鍵點鄰域內的像素點信息，提高了算法的抗噪能力，有利于匹配精度的提高。

圖6 關鍵點領域信息產生特征向量

5 結語

SIFT算法目前在軍事、工業和民用方面都得到了不同程度的應用，其應用已經滲透了很多領域，比如物體識別、犯罪現場特征提取、三維建模和指紋與人臉識別等。圖像中包含的不變特征用SIFT算法可以得到有效的提取，但是如果在圖像中可利用的特征點較少、由圖像成像質量造成的圖像邊緣模糊的情況下，都不能很好的確定特征點。目前基于SIFT算法發展出來的立體匹配技術都是以上述四個方面內容為基礎的。

［1］張廣軍.機器視覺［M］.北京:科學出版社，2005:24-27.

［2］徐德，譚民，李原.機器人視覺測量與控制［M］.2版.北京:國防工業出版社，2011:121-122.

［3］Linda G.Shapiro，George C.Stockman.計算機視覺［M］.北京:機械工業出版社，2005:1-8.

［4］鐘玉琢，喬秉新，李樹青.機器人視覺技術［M］.北京:國防出版社，1994:132-133.

［5］DavidA.Forsyth，Jean Ponce.計算機視覺［M］.北京:電子工業出版社，2004:3-12.

［6］Makoto Sato.An Active Stereo Vision System Based on Neural Pathways of Human Binocular Motor System［J］.Journal of Bionic Engineering，2007(4):185-192.