便攜心電傳感器的心房肥大診斷研究

陶泳任, 陳冠雄, 沈海斌

(1.浙江大學 超大規模集成電路設計研究所，浙江 杭州 310027；2.杭州易和網絡有限公司，浙江 杭州 310012)

0 引 言

隨著科學技術的發展，人們的生活水平得到顯著提高，人們更加關心健康問題，尤其是高血壓、心臟病等問題，這些疾病非常普遍，也常出現致命的危險情況[1]。便攜式心電傳感器技術[2]在保健、治病領域是極具實用價值的，讓人們及時獲知自己身體狀況，并及時獲得治療。現代智能傳感器系統與以往傳統傳感器顯著不同之處在于：現代傳感器包含了比較完整的計算系統，能夠在微小的設備上實現信號采集、信號處理等功能。心房肥大[3]是一種重要的心臟疾病。心房肥大分為左心房肥大、右心房肥大、雙房肥大。Cortes C等人根據統計學理論提出的支持向量機(su-pport vector machine,SVM)學習方法[5]，近年來受到了國內外學術界的廣泛重視，SVM本質是根據訓練樣本集構造出最優分類超平面，使得樣本集可以被該超平面盡可能正確地分開，并使離超平面最近的Vector與超平面之間的距離最大。選擇適用于心房肥大識別的核函數、擴展其算法，讓SVM在心房肥大識別特定領域發揮得更出色。本文所研究的算法適用于便攜式心電傳感器的應用。

1 小樣本情況下的分類器

分類器的分類準確率常與訓練樣本數據量密切相關，由于心房肥大數據匱乏，故對小樣本情況進行研究。文中使用MGH/MF數據庫中32例左心房肥大心電數據和100例正常心電數據作為訓練和識別的數據[5]。在Matlab中對比了邏輯分枝判斷、模糊推理、神經網絡、統計模型4種不同分類方法在小樣本訓練情況下的分類正確率。實驗結果如表1所示。

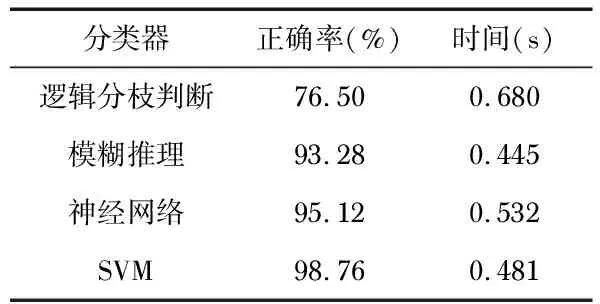
表1 4種方法性能對比

邏輯分枝判斷法是最早用于心電信號分類的方法，這種方法模仿心電圖(ECG)專家對心電信號的診斷，對噪聲比較敏感。

模糊推理[6]中需要求解隸屬函數，而隸屬函數求解沒有客觀的評定標準，使得模糊推理在心電信號的識別中受到限制。

選取三層的神經網絡[7]，使用BP神經網絡算法，并將神經網絡用于識別。

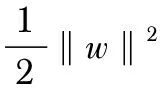
神經網絡和SVM都在心電識別中有廣泛的應用，神經網絡具有較強的容錯性和魯棒性，但神經網絡隱含層層數和網絡節點數的選取沒有一定的理論依據，這也影響了神經網絡的發展。SVM是基于統計學習理論和結構風險最小化原則的分類器，是針對小樣本學習問題的一個理論框架。SVM對模式分類的準確率一般要高于神經網絡。因此，采用SVM來實現心電診斷，以充分發揮SVM在模式識別上的優勢。

2 基于SVM的分類器融合

2.1 選擇核函數

數據集是在Matlab的Libsvm[8]下進行訓練的，仍然使用32例左心房肥大數據和100例正常心電數據，使用了不同的參數經過優化的核函數來找到最適用于心房肥大識別的映射函數，實驗結果表明：高斯核函數的SVM產生了最少的錯誤率，實驗結果如表2所示。后文中分類器融合是基于高斯SVM基礎上進行研究。

表2 4種算法準確率比較

2.2 構建融合分類器

為了在總體上達到比單獨使用某一種分類器更好的性能，將不同的分類器結合起來，發掘各自的優點。由于不同的分類器適應于不同的模式[9]，本文還將構建的分類器與其他融合的分類器進行了比較，證明所設計的分類器是適用于心房肥大識別的。

設計融合分類器的目標是讓輸出結果有更高的可信度，放棄那些離SVM超平面距離比較近的Vector的分類，這些心電的診斷不適合讓自動分類器得出結論，還需要心電圖專家的更復雜的診斷，降低分類器錯誤率，以此來提高分類器的可信度。

定義分類器拒絕分類的區域為拒絕域，示意圖如圖1所示，在超平面一邊為-1，在超平面另一邊為1，在靠近超平面的區域設定一個拒絕域，在拒絕域范圍內的Vector不作分類。

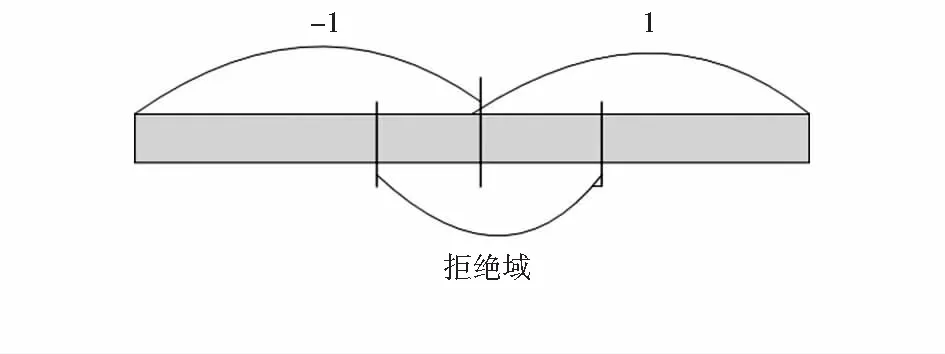
圖1 拒絕域示意圖

接著要研究權衡拒絕域設置的問題。直觀上可以知道拒絕域越大，分類的準確率越高，當拒絕域包含了所有Vector空間，則分類器對所有Vector都進行拒絕，此時可認為分類準確率達到100 %；拒絕域越小，分類器的分類準確率會下降，當拒絕域趨向于0時，在超平面附近的Vector會出現錯誤分類錯誤的情況。從2個方面進行實驗：拒絕域對稱性、拒絕域閾值計算。

3 實驗與分析

3.1 對稱拒絕域

選擇與超平面的距離為{0，0.1，0.2，0.4，0.7}的對稱超平面，形成拒絕域。實驗結果如圖2所示，描述了拒絕域閾值與分類準確率的關系。

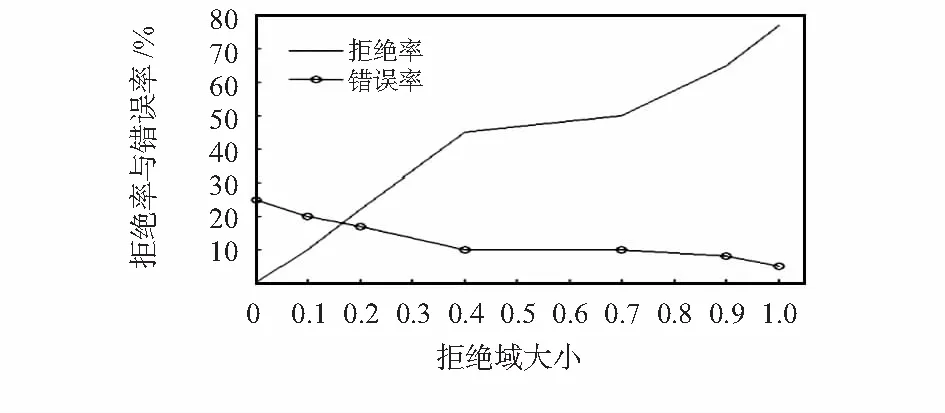
圖2 拒絕率與錯誤率關系圖

3.2 非對稱拒絕域

選擇與超平面的距離為{0，0.1，0.2，0.4，0.7}的正反方向兩個超平面，不同閾值兩兩組合形成非對稱拒絕域。實驗結果如圖3所示，描述了拒絕域閾值與分類準確率的關系。

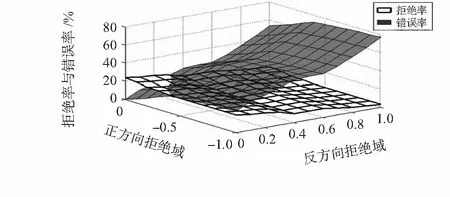
圖3 拒絕率與錯誤率關系圖

3.3 對稱與非對稱拒絕域比較

對稱拒絕域、非對稱拒絕域,閾值、錯誤率之間的關系如圖4所示。在保證高準確率、高可信度的情況下，選擇較小的拒絕域，因此,非對稱拒絕域是較好的選擇。

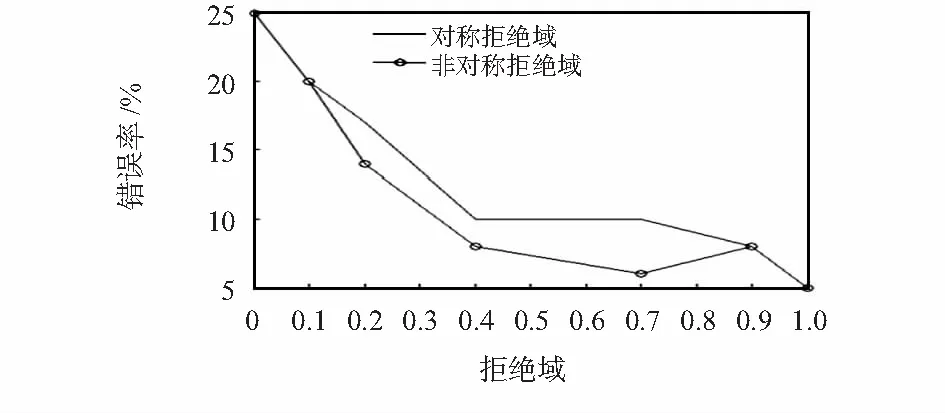
圖4 對稱與非對稱閾值比較

3.4 與其他分類器的比較

第二節中通過SVM與其他分類模式的比較，展現了SVM在小樣本識別上的優勢。這里在基于GSVM的基礎上，證明SVM-R比SVM與其他分類器融合在心房肥大識別上更具優勢。選取SVM和邏輯回歸(logistic regression,LR)融合的分類器SVM-LR[10]，SVM和K最近鄰(K-nearest neighbor，K-NN)算法融合的分類器SVM-KNN分類器[11]作為比較對象。選取不同拒絕率，比較分類錯誤率。實驗結果如表3所示。

選擇非對稱拒絕域，選擇合適的拒絕閾值能達到較好的分類正確率與可信性，該分類器適合于心房肥大的診斷。

4 結 論

本文比較了基于統計模型的分類方法與其他的分類方法，小樣本情況下，統計模型在小樣本訓練情況下優化得更好，而且,本文將SVM與拒絕域分類器進行融合，使得心房肥大的診斷結果更加具有可信度，減少因診斷錯誤產生的醫療事故的可能性。將SVM-R分類器應用到便攜式心電傳感器系統中，實現便攜式心房肥大識別是非常適用的。

表3 4種分類器比較

參考文獻:

[1] 孫 燕,毛羽青,尹東屏,等.鹽城地區心腦血管疾病發病率特征及其預報方法初探[C]∥第 28 屆中國氣象學會年會論文集，2011.

[2] Chi Y M,Jung T P,Cauwenberghs G.Dry-contact and noncontact biopotential electrodes:Methodological review[J].IEEE Reviews in Biomedical Engineering,2010,3:106-119.

[3] 張夏琳,盧喜烈.心房心室肥大的心電圖診斷[J].江蘇實用心電學雜志,2013,22(3):643-652.

[4] Cortes C,Vapnik V.Support-Vector networks[J].Machine Learning,1995,20(3):273-297.

[5] Goldberger A L,Amaral L A N,Glass L,et al.PhysioBank,Phy-sioToolkit,and PhysioNet:Components of a new research resource for complex physiologic signals[DB/OL]:MGH/MF.[2000—06—13].http:∥circ.ahajournals.org/cgi/content/full/101/23/e215].

[6] Pavlopoulos S,Kyriacou E,Koutsouris D,et al.Fuzzy neural network-based texture analysis of ultrasonic images[J].Engineering in Medicine and Biology Magazine,IEEE,2000,19(1):39-47.

[7] Purushothaman G,Karayiannis N B.Quantum neural networks (QNNs):Inherently fuzzy feedforward neural networks[J]. IEEE Transactions on Neural Networks,1997,8(3):679-693.

[8] Sun F,Belatreche A,Coleman S A,et al.Evaluation of LibSVM and mutual information matching classifiers for multi-domain sentiment analysis[C]∥The 23rd Irish Conference on Artificial Intelligence and Cognitive Science,Dublin City University:Compu-ter Science Research Institute，2012:106-118.

[9] 劉遵仁,吳耿鋒.一種新的基于約簡的多分類器融合算法[J].計算機工程與應用,2012,48(34):11-16.

[10] Chang Y I.Boosting SVM classifiers with logistic regression[J/OL].[2003—03-01].http:∥www.stat.sinica.edu.tw/library/c_tec_rep/pdf,2003.

[11] Uyar A,Gurgen F.Arrhythmia classification using serial fusion of support vector machines and logistic regression[C]∥4th IEEE Workshop on Intelligent Data Acquisition and Advanced Computing Systems:Technology and Applications,IDAACS 2007,IEEE,2007:560-565.