基于帳篷混沌觀測矩陣的圖像壓縮感知*

劉敘含， 申曉紅， 姚海洋， 鄧 欣

(1.西北工業大學 航海學院，陜西 西安 710000；2.湛江南海西部石油勘察設計有限公司，廣東 湛江 524057)

0 引 言

傳統的奈奎斯特采樣定理要求信號的采樣速率必須達到信號最高頻率的2倍或2倍以上才能夠精確重構原始信號。2004年,Donoho D L和Candès Emmanuel等人提出的壓縮感知(compressed sensing，CS)理論突破了奈奎斯特定理的局限，是近年來信息處理領域的一個重大突破[1～3]。

壓縮感知包括以下三方面內容：信號的稀疏表示、觀測矩陣的設計和信號的重構。觀測矩陣在信號采樣和數據重建環節發揮著至關重要的作用。常用的觀測矩陣分為三類。第一類包括高斯隨機觀測矩陣、貝努利隨機觀測矩陣等，這類隨機觀測矩陣需要大存儲空間、高計算復雜度；第二類包括部分傅里葉矩陣、部分哈達瑪矩陣等，這類觀測矩陣只與時域、頻域稀疏的信號不相關，不具有普適性；第三類包括托普利茲矩陣、二進制稀疏矩陣等，這類觀測矩陣是針對某一特定信號而設計的，應用范圍存在很大的局限性。目前，各文獻中最常用的觀測矩陣為高斯隨機觀測矩陣。

針對目前常用的三類觀測矩陣存在的缺陷，本文提出了一種基于帳篷混沌序列的觀測矩陣的構造方法。與典型的隨機觀測矩陣相比，帳篷混沌觀測矩陣具備了混沌系統優異的偽隨機性，易于產生和實現。通過對二維圖像信號進行仿真實驗，結果表明:所設計的帳篷混沌觀測矩陣不僅在信號重構時的性能優于隨機觀測矩陣，并且在硬件實現、存儲方面的優勢也遠遠大于隨機高斯觀測矩陣。

1 壓縮感知理論

壓縮感知理論的核心思想是將壓縮與采樣合并進行。該理論指出，只要信號是可壓縮的或在某個變換域是稀疏的，那么就可以用一個與變換基不相干的觀測矩陣將高維信號投影到一個低維空間上，然后通過求解優化問題即可從這些少量的投影中以高概率重構原始信號，可以證明這些少量的投影包含了重構信號所需的足夠信息。

設X為實值有限的一維離散信號，長度為N，它可以看作是RN空間的N×1維列向量。若信號X在一個正交變換基組成的變換矩陣ψ∈RN×N下能表示為

X=ψΘ.

其中,Θ=[θ1,θ2,…,θN]T稱為信號X在基矩陣ψ下的投影系數向量。理想情況下，若Θ中非零值的個數K?N，則認為X在ψ域中是K稀疏的。在實際中，對于由少量幅度較大的值和大量幅度較小的值組成的信號，Cande E J和Tao T在研究信號的稀疏表示時提出可以通過變換系數的衰減速度來衡量變換基的稀疏表示能力，并指出信號如果在某域的變換系數滿足具有冪次(power-law)速度衰減，就可以用壓縮感知理論得到恢復[4]。

利用一個與ψ不相關的觀測矩陣Φ∈RM×N對信號進行觀測，從而獲得觀測值Y

Y=ΦΘ=ΦΨ-1X=ACSX.

其中,Y是包含M個線性觀測值的一維列向量，而這些少量的觀測值包含了重構原始信號X的足夠信息。理論上，觀測矩陣和稀疏信號之間應滿足有限等距性質(restricted isometry property，RIP)[5]。

信號的重構是指，在已知ψ,Φ,Y的條件下，選擇合適的重構算法恢復原始信號X。由于M?N，即方程的個數遠遠小于未知數的個數，因此,從Y中恢復X是一個欠定問題，其解不唯一。然而，由于X是K稀疏的，可在滿足一定條件下通過求解一個非線性優化問題,從ψ,Φ,Y中近乎完美地重建信號[6]。

2 基于混沌觀測矩陣的壓縮感知

高斯隨機觀測矩陣之所以能夠作為最常用的觀測矩陣，主要在于它與絕大多數正交矩陣不相關，并且當M≥cKlg(N/K)時隨機高斯矩陣便以極高的概率滿足RIP性質，其中,c是一個很小的常數，K為稀疏度[7]。

雖然隨機觀測矩陣具有以上優點被普遍地作為觀測矩陣，但所有的隨機觀測矩陣都存在以下不足：1)隨機矩陣的產生具有不確定性，需要通過大量的實驗求均值的方法來降低不確定性對實驗結果帶來的影響；2)在實際應用中，該類觀測矩陣計算復雜度高，占用存儲空間大，而且硬件難以實驗。

混沌理論揭示了確定性與隨機性的統一，由混沌系統產生的序列具有優異的偽隨機性[8]，易于產生和重現。與隨機系統相比，混沌系統的參數和初始值一旦確定，混沌系統每一時刻的狀態是可以完全重現的，存儲和傳輸的參數較少，可大大減少存儲空間和傳輸帶寬的壓力。由于混沌序列可以克服隨機觀測矩陣的不足，可以考慮將其應用在壓縮感知觀測矩陣的設計中。

帳篷映射[9]是一種應用相當廣泛的離散混沌系統，其映射方程的數學表達式為

xn+1=a-(1+a)|xn|.

其中,a∈(0,1)。本文仿真實驗中令a=0.999，迭代初值x0=0.01。當迭代次數n=10 000時，迭代點空間分布圖如圖1所示。

圖1 帳篷映射迭代點空間分布圖

整體來看，所有迭代點均勻地分布在(-1,1)的區間內，遍布了整個有界區域，但各個點卻又是雜亂分布，沒有規律，這正體現了混沌序列的偽隨機性。利用迭代產生的序列{x1,x2,…，xn}設計帳篷混沌觀測矩陣如下

3 仿真實驗

本節利用3種典型的隨機觀測矩陣，即高斯隨機觀測矩陣、貝努力觀測矩陣、離散余弦觀測矩陣與所設計的帳篷混沌觀測矩陣進行對比，分別對數據量不同的二維圖像信號進行壓縮和重構。

分別以40×40的二值紫荊花圖像和70×70的二值字母圖像為例，原始圖像如圖2(a),(b)所示。對2個圖像進行離散余弦變換(DCT)，得到頻域稀疏信號，如圖3、圖4所示；再分別采用帳篷混沌觀測矩陣和3種典型的隨機觀測矩陣對稀疏信號進行觀測，得到壓縮信號；最后采用匹配追蹤(MP)算法[10]進行重構。

圖2 原始圖像

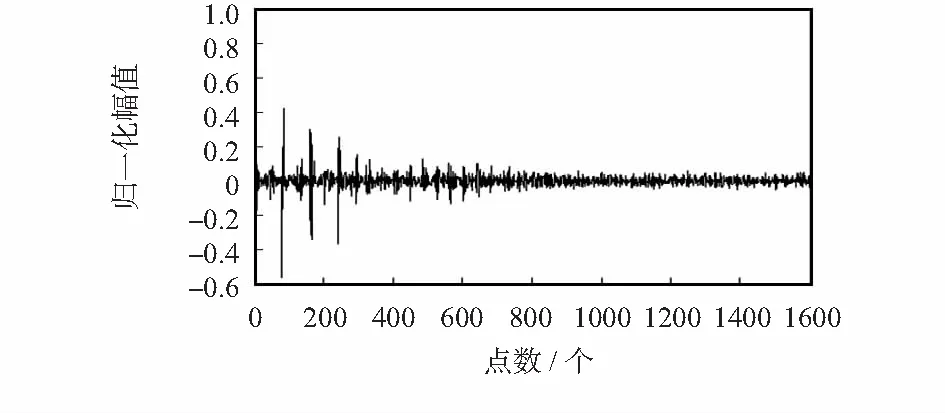
圖3 二值紫荊花圖像的DCT波形

圖4 二值字母圖像的DCT波形

利用不同觀測矩陣對紫荊花圖像進行觀測，當觀測值M=1000時，重構結果如圖5所示。

圖5 M=1 000時不同觀測矩陣的重構結果

利用不同觀測矩陣對字母圖像進行觀測，當觀測值M=3 000時，重構結果如圖6所示。

圖6 M=3 000時不同觀測矩陣的重構結果

可以直觀地看出:采用帳篷混沌觀測矩陣進行觀測時，紫荊花圖像和字母圖像的重構效果更佳。當觀測值不同時，對2幅圖像采用不同觀測矩陣得到的重構誤碼率分別如圖7、圖8所示。

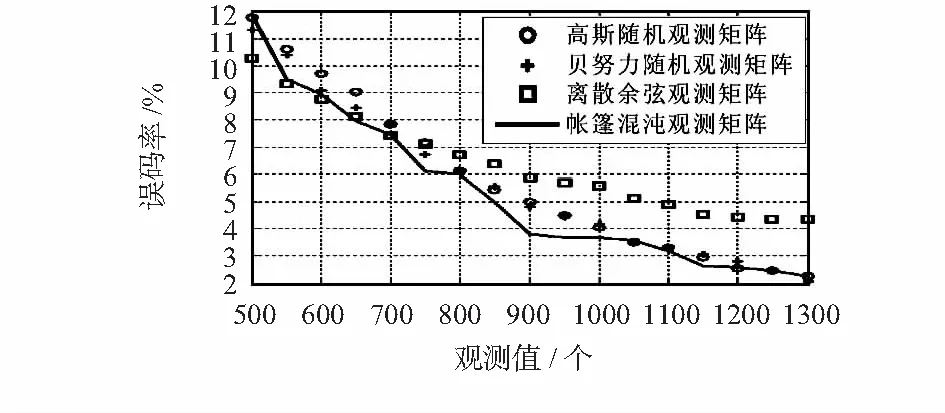
圖7 二值紫荊花圖像重構結果對比

圖8 二值字母圖像重構結果對比

圖7、圖8表明:采用帳篷混沌觀測矩陣，其重構的誤碼率性能也是優于隨機觀測矩陣的。由于隨機觀測矩陣的每一次產生都具有不確定性，為了減小不確定性對仿真結果的誤差影響，其誤碼率是1000次蒙特—卡洛仿真求平均的結果。而帳篷混沌觀測矩陣具有確定性，只需一次仿真即可得到結果，這是帳篷混沌觀測矩陣的優勢之一。

通過仿真驗證了帳篷混沌觀測矩陣的確克服了隨機觀測矩陣的不足：1)帳篷混沌觀測矩陣的參數和初始值一旦確定，可以在任何時刻完全重現，克服了隨機觀測矩陣需要大量實驗求均值來降低不確定性對實驗的影響的缺陷；2)隨機觀測矩陣在仿真實驗中需要存儲和傳輸整個巨大的

觀測矩陣中的所有元素。例如:二值字母圖像的仿真實驗中，當M=3000時，高斯隨機觀測矩陣需要存儲M×N=3 000×70×70=1.47×107個數據。而帳篷混沌觀測矩陣只需要存儲和傳輸一個帳篷序列表達式xn+1=a-(1+a)|xn|和2個參數初始值a=0.999,x0=0.01即可，大大節省了存儲空間和傳輸帶寬、降低了計算復雜度。當數據量更大時，帳篷混沌觀測矩陣的優勢會更加明顯。

4 結 論

通過對二維圖像信號的仿真實驗表明:本文所設計的帳篷混沌觀測矩陣能夠以高概率重構信號,其重構性能不但優于目前常用的隨機觀測矩陣，而且克服了隨機觀測矩陣在不確定性、硬件實現、存儲方面的缺陷。

雖然壓縮感知理論具有廣闊的應用前景，一經提出就受到了廣泛關注，但其理論還不夠完善。關于稀疏性、有限等距約束原則在實際中的驗證是一個組合復雜度問題，極為復雜，尋求一種嚴密并且在實際中易于驗證的準則是有必要的。

參考文獻:

[1] Candès Emmanuel.Compressive sampling[C]∥Int’l Congress of Mathematics,Madrid,Spain,2006:1433-1452.

[2] Donoho D L.Compressed sensing[J].IEEE Trans on Info Theory,2006,52(4):1289-1306.

[3] Candès Emmanuel ,Wakin Michael.An introduction to compre-ssive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[4] Candès E J,Tao T.Near optimal signal recovery from random projections: Universal encoding strategies[J].IEEE Trans on Info Theory,2006 ,52(12):5406-5425.

[5] 戴瓊海，付長軍，季向陽.壓縮感知研究[J].計算機學報,2011,34(3):425-434.

[6] Baraniuk R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[7] Nabaee M,Labeau F.Restricted isometry property in quantized network coding of sparse messages[C]∥IEEE Global Communications Conference(GLOBECOM),Anaheim,CA,IEEE,2012:112-117.

[8] 羅松江，丘水生，駱開慶.混沌偽隨機序列的復雜度的穩定性研究[J].物理學報，2009,58(9):6045-6049.

[9] 單 梁，強 浩，李 軍，等.基于Tent映射的混沌優化算法[J].控制與決策，2005,20(2):179-182.

[10] 石光明，劉丹華，高大化，等.壓縮感知理論及其研究進展[J].電子學報，2009，37(5):1070-1081.