極坐標導引頭基于全像平面的盲區跟蹤策略*

郭玉甫，張 平

（北京航空航天大學自動化科學與電氣工程學院，北京 100191）

0 引言

滾仰式導引頭結構緊湊，能大離軸角跟蹤，是新一代近距格斗空空導彈的重要組成部分。但其小離軸角錐形盲區是由其結構導致的一個必須解決的問題。目前國內研究出的跟蹤原理大都是采用根據目標在探測器位置與當前框架偏轉角計算角度指令增量的方式。具體有較傳統的根據運動學關系，通過光軸到視線的兩種空間轉動方式解算角度指令增量，其指令優化需要通過邏輯判斷［1－2］;也有較先進的基于Paden-Kahan子問題求解角度指令增量，應用最小角增量準則對運動學逆解進行指令優化［3］。在這種指令架構下的過頂控制策略主要包括指令預測及分區域變參數控制策略［2，4］。由于探測器本身處在劇烈運動中，所以相較于角度指令增量，基于全像平面的指令計算與優化方式［5］得出的角度指令更適合進行動態規劃和指令預測。文中在此指令方案的基礎上改進了其中的坐標系旋轉判據，并在分析目標運動模式的基礎上設計了一種過頂跟蹤策略。

1 坐標系定義

極坐標導引頭外框滾轉，內框俯仰，坐標系定義與目標成像幾何關系如圖1所示。圖1中點o為兩個框架軸的交點，f為o到探測器瞬時成像平面中心的距離。

載體基座坐標系oxbybzb（簡稱基座坐標系或載體坐標系）與穩定平臺載體固連。經過繞x軸滾轉后得外框坐標系oxoyozo，oxoyozo繞y軸俯仰后得內框坐標系oxpypzp。初始坐標系oxiyizi初始時刻與載體坐標系oxbybzb重合，其后坐標軸方向相對慣性空間保持不變，只隨載體平移。在仿真中給目標運動提供慣性空間。

像球面是以點o為中心、探測器焦距f為半徑的球面，目標與點o的連線與像球面交點稱為目標的像點，光軸與像球面交點稱為光點，可以分別用來表示目標視線與光軸位置。為更方便直觀起見，以圖1中oxb（xo）與像球面交點Q為中心將像球面展開成平面稱為全像平面，進而可在全像平面上表示目標位置，并由此計算框架偏轉指令。

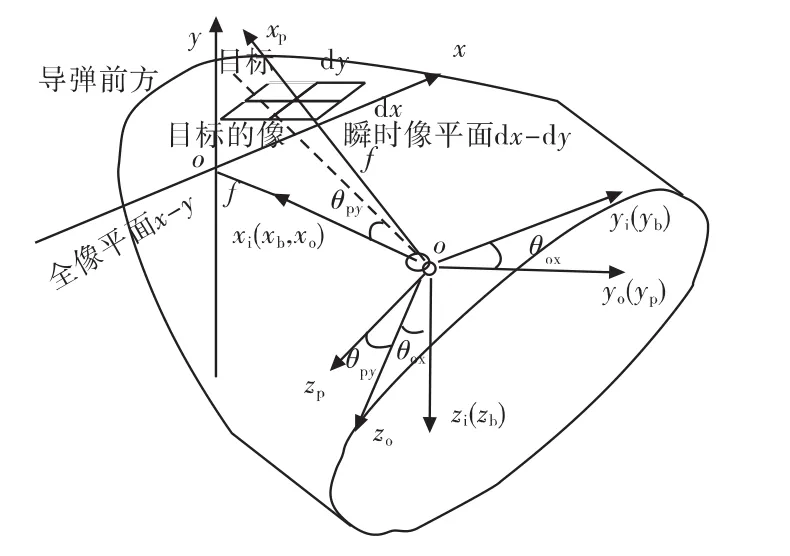
圖1 坐標系定義

由圖1可得，由載體坐標系三維坐標（xb，yb，zb）得到的全像平面二維坐標（x，y）為:

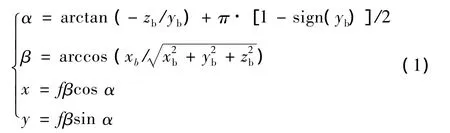
式（1）中，α、fβ分別為點在全像平面的極角（取值范圍為－π/2～3π/2）與極徑。β是點在載體坐標系的離軸角。對任一點p，其α，β角如圖2所示。

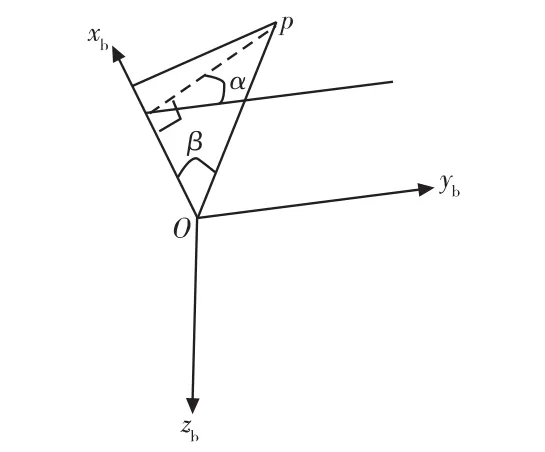
圖2 載體坐標系上點的極角α與離軸角β示意圖

2 指令計算與優化［5］

系統采取角度跟蹤方式，由攝像頭探測及圖像處理得到的目標在瞬時像平面上的像點坐標 （d x，d y），可直接構造像點在內框坐標系的坐標為（f，d x，－d y）。通過轉換得到該點在載體坐標系坐標。再通過式（1）即可得目標對應的全像平面像點坐標（x，y），進而構造框架偏轉指令。

2.1 初級指令公式

由圖1中幾何關系得框架偏轉角度指令:

式中:θoxc和θpyc分別是外框滾轉角和內框俯仰角指令（rad），下文各個角度都采用弧度單位;f是攝像頭焦距（m）。

2.2 指令跳變與優化方式

從式（2）可以看出，當目標像點位于不同的象限，框架指令的符號不同，當像點跨越x軸時會出現指令正負符號的跳變，滾轉指令跳變幅度約為π。以其中一種情況為例，如圖3所示，當像點在x軸附近從第一象限運動到第三象限時，跨越前像點的滾轉指令為α。當前像點的滾轉角按式（2）計算為γ。顯然大于π的角β才是合理的。得到角β的方式為將全像平面坐標系順時針旋轉π/2，在新坐標系下的坐標為:（x'，y'），且 x'= －y，y'=x則β =arctan|x'/y'|+π/2。

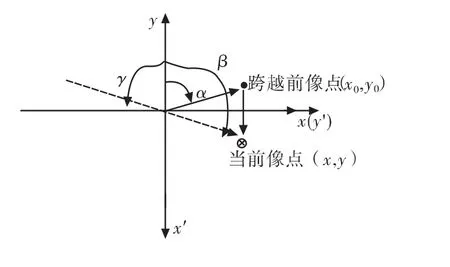
圖3 指令跳變及旋轉坐標系圖示

由上述分析總結得指令優化的方式為:

當像點跨越x軸時將像平面的x、y坐標軸以原點為中心同時旋轉+/－90°，旋轉方向與像點跨越方向相同。最后再利用坐標系旋轉公式對原來的目標像點坐標x和y進行轉換，得到目標像點在旋轉后坐標系下的坐標，對新坐標再按照式（2）計算滾轉角和俯仰角指令，同時滾轉角指令加上相應的π/2的整數倍得到最終的指令式（3）。

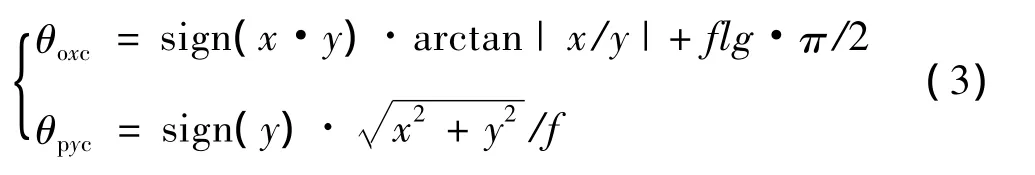
其中:（x，y）為坐標系旋轉后的目標像點坐標，flg表示坐標系順時針旋轉次數。

2.3 原始的坐標系旋轉判據

每個指令周期坐標系旋轉的判據如表1、表2所示，當前像點坐標為（x，y），前一個像點坐標為（x0，y0）。

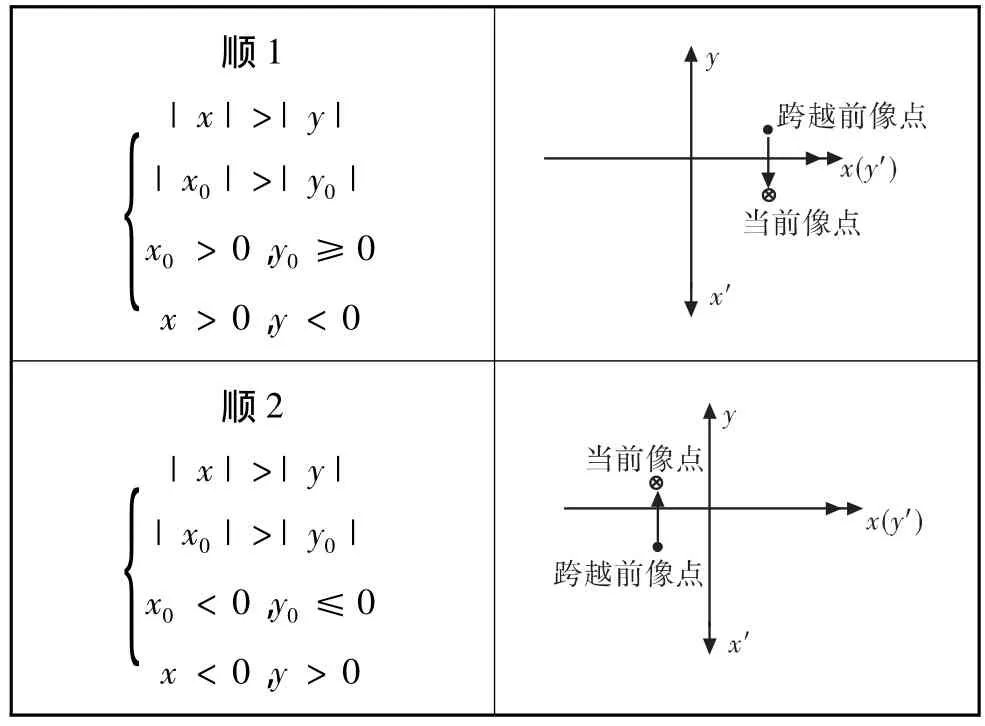
表1 順時針旋轉坐標系判據

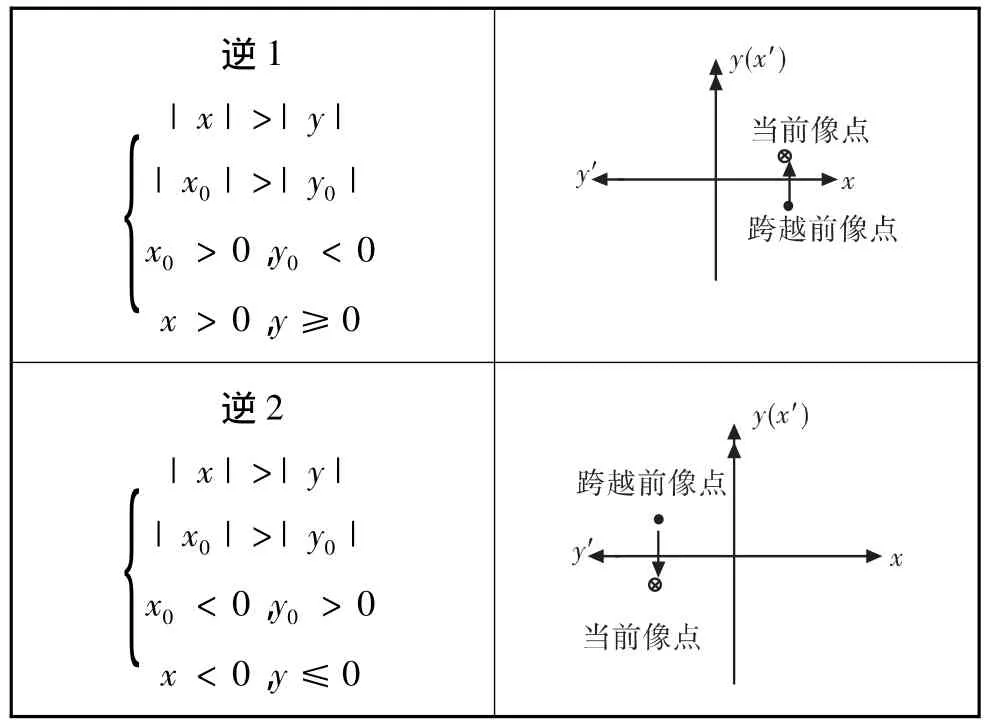
表2 逆時針旋轉坐標系判據

3 盲區分析及目標運動模式分類

3.1 盲區分析

像球面上光點對像點的跟蹤與光軸偏轉角速度之間的關系如圖4。

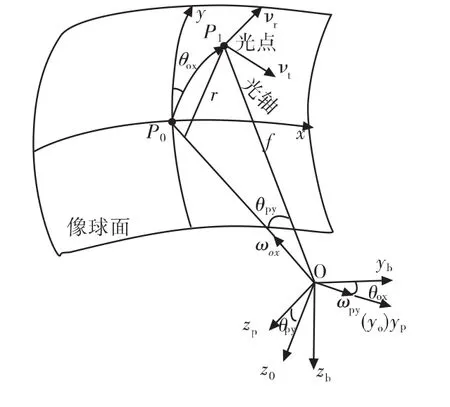
圖4 像球面上光點運動示意圖

為了分析光點對像點的跟蹤，將當前像點在像球面上的移動速度分解為徑向速度vr和切向速度vt。固定的目標視線運動角速率下，當目標視線運動對應的目標像點在像球面的速度全部為切向速度分量時，要求的滾轉框滾轉速度也最大，且這個要求的最大值隨離軸角的減小在小離軸角區域急劇增加，導致過頂盲區的產生。因此，可給定最大目標視線角速率ωt，max，外框最大滾轉角速度 ωox，max，可得能保證正常跟蹤的最小離軸角θpy，min，也即盲區界定范圍，如式（4）。

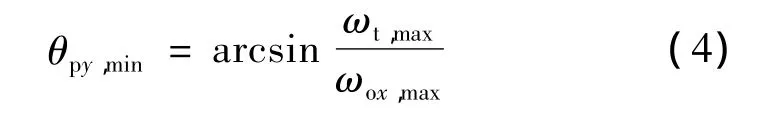
3.2 目標運動模式分類

1）目標運動模式1

運動描述:目標運動在盲區外。

由于外框所能提供的最大轉速大于目標運動的要求，可實現正常跟蹤。

2）目標運動模式2

運動描述:目標一直在盲區內運動。

由于盲區實質是體現小離軸角時框架能提供的像球面上光點切向速度的不足，因此最壞的情形即目標視線在盲區內以最大角速度繞外框滾轉軸作旋轉運動，其運動的離軸角記為α。

可以想見，這種情況下外框以極速偏轉，但滾轉角跟蹤誤差線性增加，然而失調角卻會從0到峰值作周期運動。失調角峰值產生于當光軸，目標視線和外框滾轉軸共面時，其值為2α，如圖5所示。

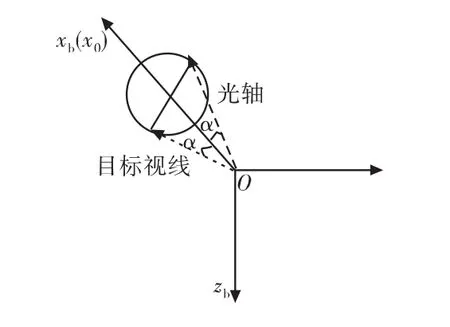
圖5 目標盲區內圓周運動最大失調角示意圖

所以目標運動情形2下的失調角≤2θpy，min，即2倍的盲區邊界離軸角。在此情況下若要保證目標不丟失，則探測器的探測角要 ≥2θpy，min。

3）目標運動模式3

運動描述:目標從盲區外進入盲區內再出來，即目標對盲區的穿越。

該運動模式體現了極坐標導引頭的奇異性［2］，目標進入盲區后，一開始外框跟蹤不上產生一定的外框跟蹤誤差，但在小離軸角盲區內此誤差并不會導致大的失調角。隨著目標視線的離軸角增大，如外框跟蹤誤差不能盡快消除，則會產生大的失調角，當失調角超出探測器探測范圍時就會形成目標丟失。

4 坐標系旋轉判據改進及盲區策略設計

由上節分析可知只有目標運動模式3才會導致目標丟失，根據其特點可設計指令策略如下:當目標在指定范圍的小離軸角區域運動時，若目標像點的極角變化過快，就使滾轉角指令保持不變，并記錄進入滾轉保持策略前的最后一個點，當策略執行條件不成立時，將最后一個點坐標看作上一個點坐標，并作為指令計算與優化的依據來形成指令。仿真表明，目標快速穿越盲區，可導致正常跟蹤丟失時（設探測器瞬時視場大小為±3°），若使用上述策略，將會產生外框保持幾個周期而后反向滾裝，同時內框變號的指令，可達到以較小的外框滾轉角速度跟蹤目標的目的，仿真表明這種情況下可有效降低跟蹤過程中的最大失調角。

4.1 旋轉坐標系判據改進

為保證在目標快速穿越盲區運動中，滾轉保持策略可以最終實現滾轉框的反向偏轉，且不論這種穿越以何種方向。需將2節中指令優化的坐標系旋轉判據作兩點改進:

1）將判據中判定需旋轉坐標系的x軸兩側扇形區縮小;

2）將判據調整為對坐標系的 x軸、y軸功能對稱。

改進后坐標系旋轉判據如表3～表4所示，當前像點坐標為（x，y），前一個像點坐標為（x0，y0），～表示非。

k用以完成改進1），可根據導引頭參數和要達到的目標視線跟蹤速率指標取值，在下面仿真中取為3。順3，順4，逆3，逆4 完成改進2）。

4.2 滾轉保持策略描述

加入策略后指令模塊輸入輸出如圖6所示。

輸出:thto xc，thtp yc為角度指令。（x last，y last）為執行策略前的最后一個目標像點全像平面坐標。s_flg表示該周期是否執行了策略，1表示是，0表示否。flg如前所述，表示全像平面坐標系順時針旋轉π/2的次數。

輸入:經延遲模塊得到的都是指相應變量的上一個周期值，后加0 來表示，如 s_flg0，flg0，x last0，y last0，thto xc0。（x，y）、（x0，y0）分別是目標像點的當前坐標和上一個周期的坐標。

指令計算與優化過程如圖7。

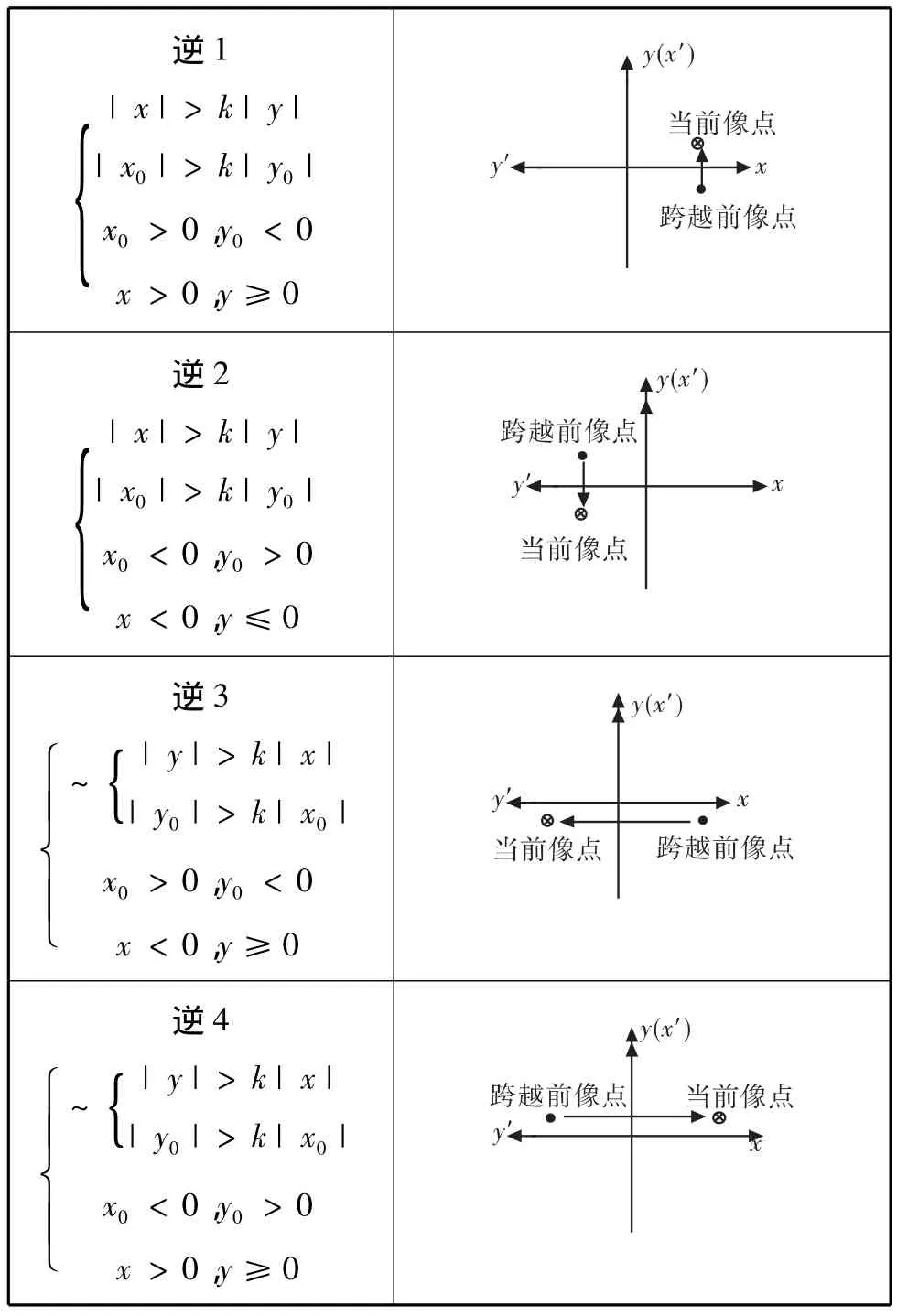
表4 改進的逆時針旋轉坐標系（逆3、逆4為新增）

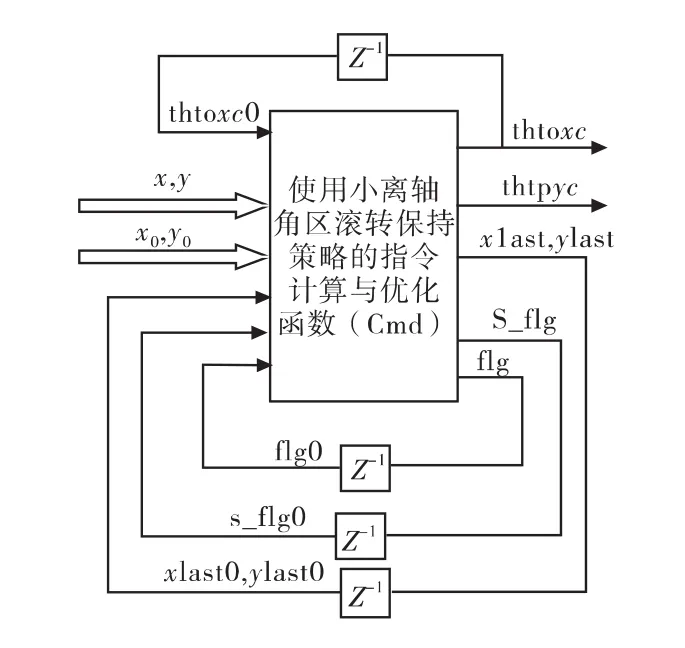
圖6 采用滾轉保持策略的指令計算與優化函數輸入輸出示意圖

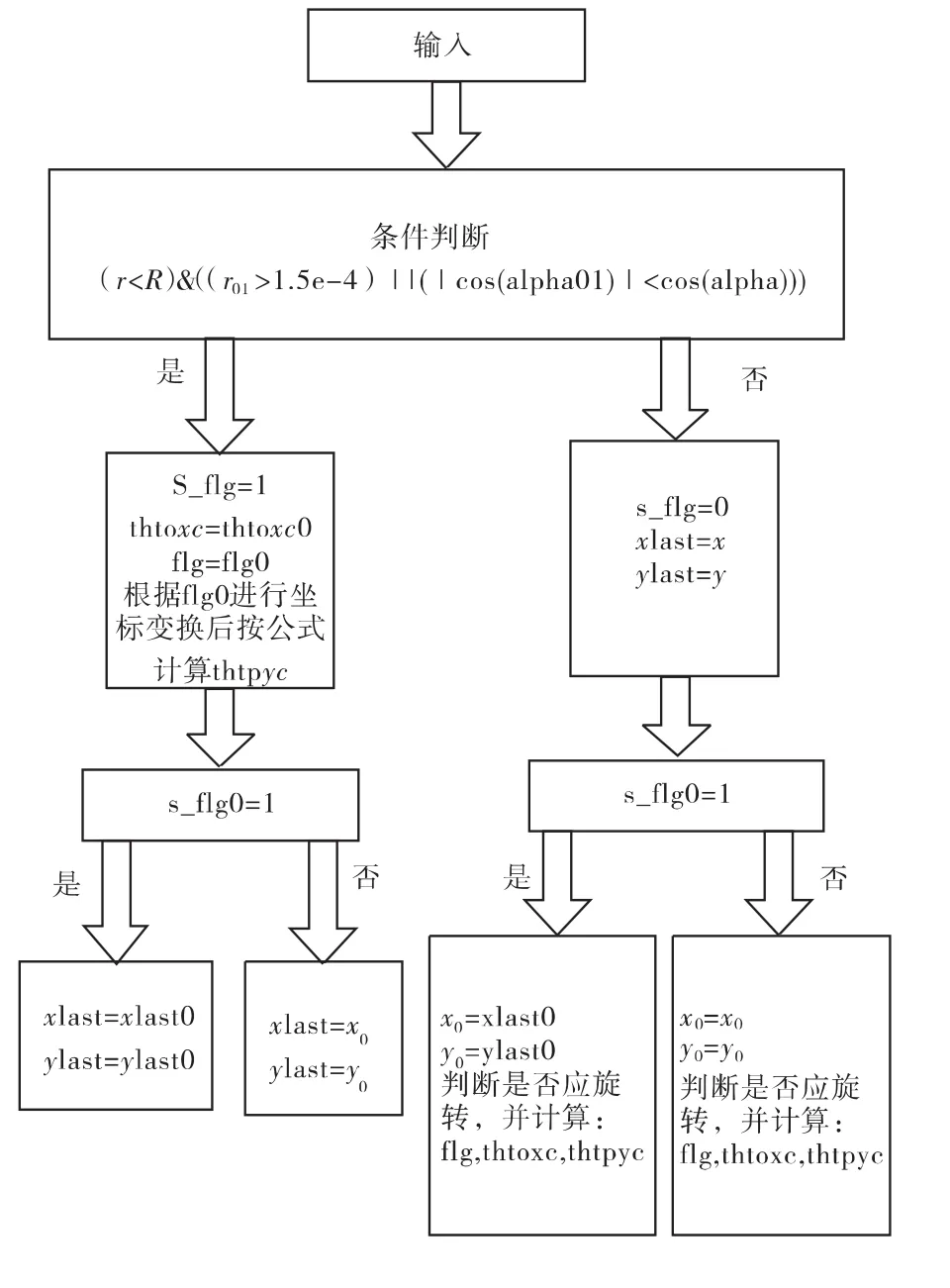
圖7 帶策略指令計算與優化過程

其中R為策略區大小，應取稍小于式（4）所計算出的盲區范圍。r01為當前像點與上一個像點的距離:，條件中加入其大于某閾值的作用是當目標視線在小離軸角策略區運動較慢時，使系統正常跟蹤，從而不影響視線穩定，使跟蹤保持小的失調角。alpha01為當前像點與上一個像點的極角差，如圖8所示。直接計算其余弦值為:標記該周期是否應用了策略，為下一周期提供判斷依據，輔助實現策略。

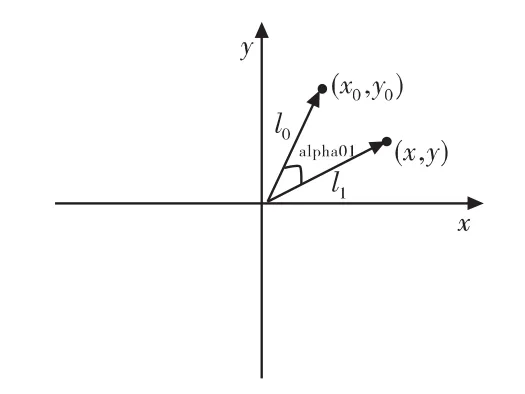
圖8 alpha01示意圖

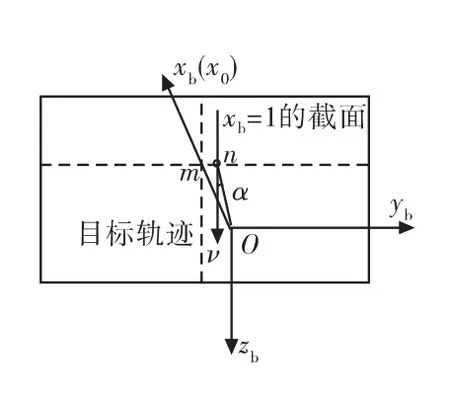
圖9 目標運動模式3軌跡

5 仿真結果及分析

5.1 目標軌跡與模型參數

此處仿真針對目標運動模式3，目標軌跡在xb=1平面給出，采用目標勻速直線穿越盲區的形式，如圖9。

目標軌跡如圖所示，運動方向豎直向下，目標像點速度v根據跟蹤指標最大目標視線角速率30°/s取為 π/6，α 取為0.3°。

導引頭外框最大滾轉角速度:1000°/s。

5.2 仿真結果

1）普通跟蹤

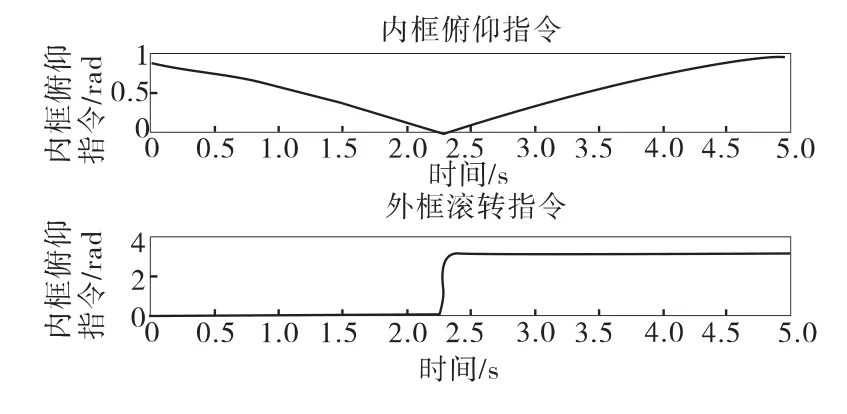
圖10 普通跟蹤框架指令

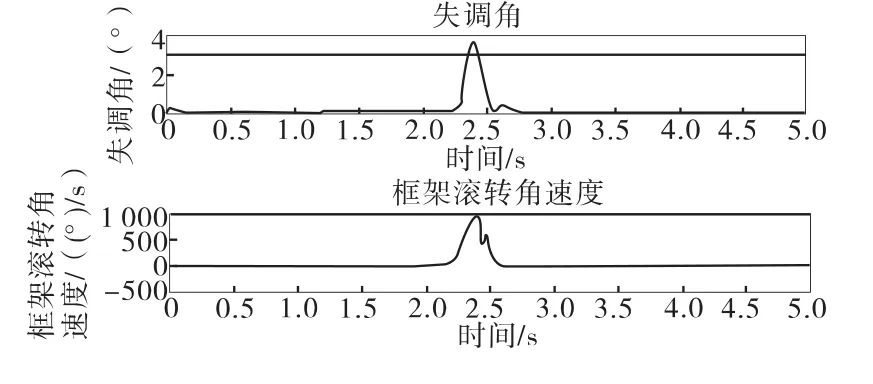
圖11 普通跟蹤失調角及外框滾轉角速度

2）策略跟蹤

仿真中，取 R=f·0.6·π/180 ，0.6°為設置的策略區邊界離軸角。

5.3 仿真結果分析

圖10顯示，由于極坐標導引頭的小離軸角盲區滾轉指令的奇異性，正常跟蹤時滾轉框角度指令有個短時間內的近似π的階躍，這導致實際滾轉框產生較大的跟蹤誤差，在目標視線離軸角增大后，這個誤差不能及時消除，導致了較大的跟蹤失調角。圖11顯示最大失調角大于3°，在實際情況中就會導致目標丟失，視線閉環不能維持。圖12顯示應用策略后，實現了滾轉框的反轉，同時俯仰框變號，圖13顯示這種情況使得跟蹤失調角的最大值減小到小于1.5°，即目標不會丟失。

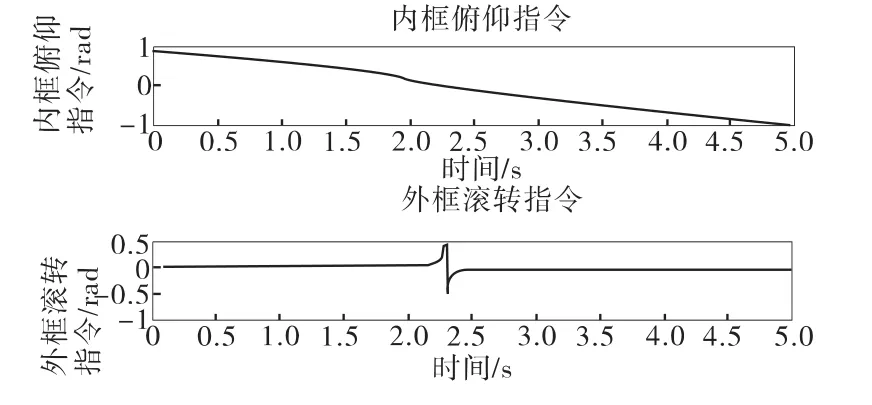
圖12 策略跟蹤框架指令

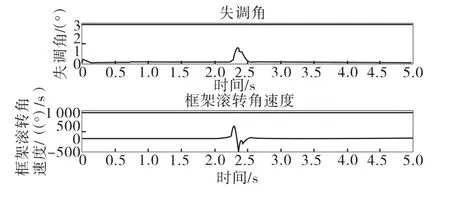
圖13 策略跟蹤失調角及外框滾轉角速度

6 結論

在小離軸角盲區，普通跟蹤方式下滾轉指令變化過快時，應用滾轉保持策略后，可在出現這種不利情況時，產生滾轉框指令反方向偏轉，俯仰框指令變號，達到跟蹤目的，可有效減小目標跟蹤過程中的最大失調角，從而減小目標丟失的概率。

［1］王志偉，祁載康，王江.滾－仰式導引頭跟蹤原理［J］.紅外與激光工程，2008，37（2）:274 －277.

［2］林德福，王志偉，王江.滾仰式導引頭奇異性分析與控制［J］.北京理工大學學報，2010，30（11）:1265－1269.

［3］朱明超，賈宏光.基于Paden-Kahan子問題求解滾仰式導引頭角增量［J］.光學精密工程，2011，19（8）:1838－1844.

［4］姜湖海.滾擺式導引頭過頂跟蹤控制策略研究［D］.長春:中國科學院長春光學精密機械與物理研究所，2012.

［5］張平，董小萌，付奎生，等.機載/彈載視覺導引穩定平臺的建模與控制［M］.北京:國防工業出版社，2011，92－94.