平面向量中不得不提的一個恒等式

●單長松 (浙江師范大學數理與信息工程學院教育碩士 浙江金華 321004)

平面向量中不得不提的一個恒等式

●單長松 (浙江師范大學數理與信息工程學院教育碩士 浙江金華 321004)

高中數學中存在著大量等量關系，如立方差(和)公式、二項展開式、兩角和與差公式等.在高中數學中常能見到這些等量關系的身影，這也是高中教學重點關注的對象.但有些等量關系看似冷門甚至課本上都不出現，但它在問題解決過程中卻能起到立竿見影的效果，實現對問題的快速“秒殺”.

1 極化恒等式

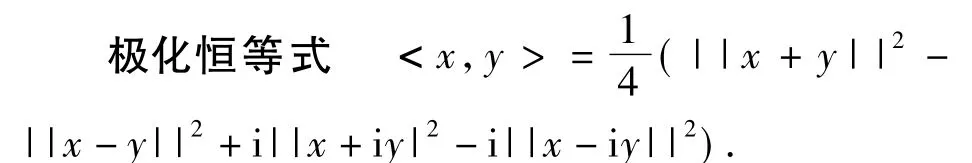
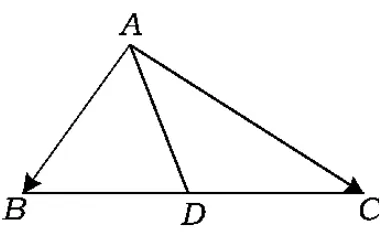
圖1

極化恒等式最初出現于高等數學中的泛函分析，它表示數量積可以由它誘導出的范數來表示.把這個極化恒等式降維至二維平面得

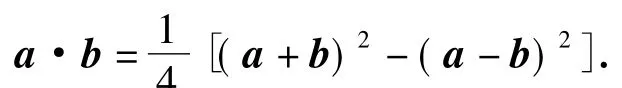
2 極化恒等式的應用

自向量引入高中數學以后，由于它獨特的性質(代數與幾何的橋梁)，在近幾年全國各地的高考中迅速成為創新題命制的出發點，在浙江省數學高考中尤為突出，也出現了一些非常精美的向量題.

這個問題的本質就是極化恒等式.

下面我們再來看2013年浙江省數學高考選擇題第7題：

(2013年浙江省數學高考理科試題)

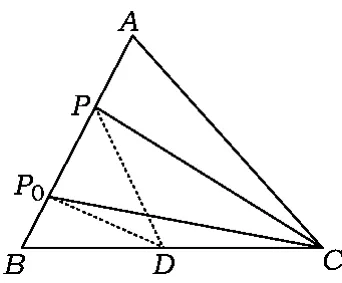
圖2

分析如圖2，取 BC的中點 D，聯結 PD，P0D，在△PBC內使用極化恒等式得在△P0BC內使用極化恒等式得

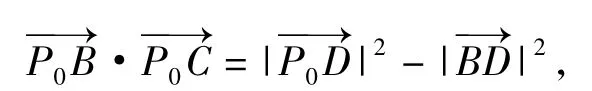
由條件知恒有PD≥P0D，即P0D⊥AB，故AC=BC.

很多一線教師都認為這個題目在10個選擇題中是最難的，應該放在壓軸的位置.筆者卻不這樣認為，其實這個題目只是在例1的基礎上對極化恒等式的應用靈活化，步子邁得更大一些而已.這個題目的姊妹題也出現在2013年浙江省高中數學聯賽中.

圖3

例3如圖3，已知直線AB與拋物線y2=4x交于點A，B，M 為 AB 的中點，C 為拋物線上一個動點，若C0滿足則下列一定成立的是( ).

A.C0M⊥AB

B.C0M⊥l，其中l是拋物線過點C0的切線

C.C0A⊥C0B

即拋物線y2=4x上所有點到M的距離最近的點即為C0，故以M為圓心、MC0為半徑的圓與拋物線內切.故選B.

除此之外，還有許多優秀的題目.

例4設正方形ABCD的邊長為4，動點P在以AB為直徑的圓弧上(如圖4所示)，則的取值范圍是 .

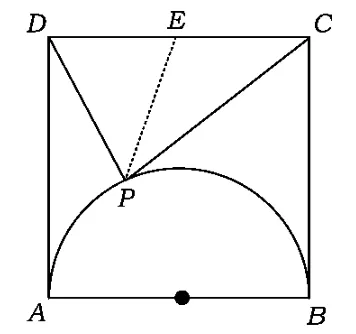
圖4

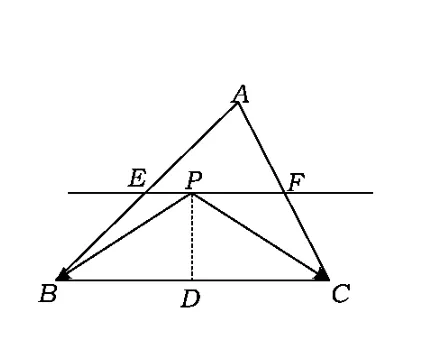
圖5

分析取CD中點E，聯結PE，在△PDC內使用極化恒等式得

3 極化恒等式帶來的反思

(1)極化恒等式源于教材又高于教材.在△ABC中，

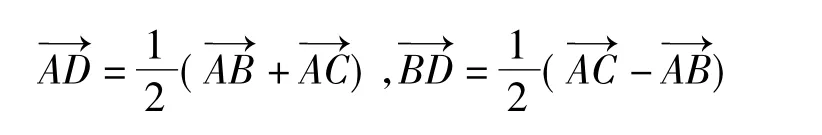
是課本上出現的2個重要的向量三角關系，而極化恒等式無非就是這2個公式的逆用.

(2)具有三角幾何背景的數學問題利用極化恒等式考慮尤為簡單，讓“秒殺向量”成為另一種可能.

(3)向量是連接代數與幾何的橋梁，由于向量的坐標運算引入，向量與代數的互換運算可以說是深入人心，而與幾何的運算聯系略顯單薄.而極化恒等式恰恰彌補了這個缺憾，可以說極化恒等式應該是把向量的數量積問題用形象的幾何圖形展示得淋漓盡致.