由教材母題解析2014年中考復習策略

●邱亦欣 (南京外國語學校 江蘇南京 210008)

由教材母題解析2014年中考復習策略

●邱亦欣 (南京外國語學校 江蘇南京 210008)

近幾年各省市的中考數(shù)學試題突出了對數(shù)學思想方法、數(shù)學理性思維及數(shù)學實際應用能力的考查，注重通性、通法，淡化解題技巧.多數(shù)試題與課本例題、習題相近，有的直接由教材母題變形而來，即使是要求較高的“壓軸題”的解題思路和方法也大都能在課本上找到“原型”，由此啟發(fā)我們在中考復習階段一定要回歸課本，夯實基礎，以不變應萬變.

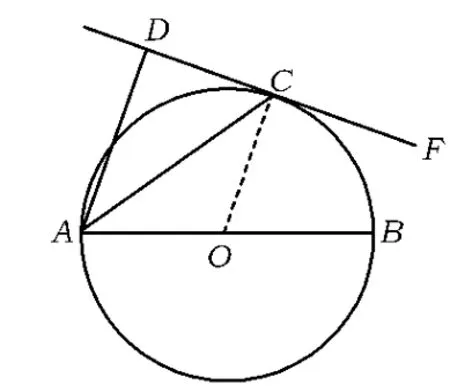
圖1

蘇教版《數(shù)學》九年級上冊第153頁的第9題如下：

母題如圖1，AB為⊙O的直徑，C為⊙O上一點，AD和過點C的切線互相垂直，垂足為 D，若∠BAD=80°，求∠DAC的度數(shù).

分析要求∠DAC的度數(shù)，可考察∠DAC與已知角∠BAD的關系，“遇切點連半徑”，聯(lián)結OC.

由OC∥AD及OC=OA可得AC平分∠BAD.

解 如圖1，聯(lián)結OC.由DC切⊙O于點C，知

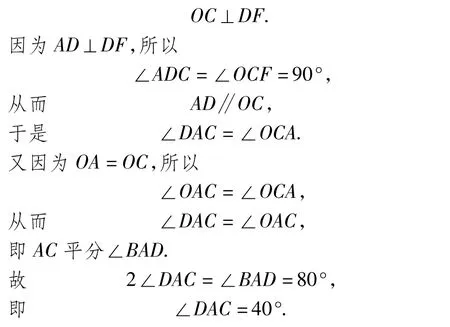
這道計算題可改為更一般性的證明題：

如圖1，已知AB為⊙O的直徑，C為⊙O上一點，AD和過點C的切線互相垂直，垂足為D，求證：AC平分∠DAB.

我們還可以作如下的變形和探究：

變形1交換題設與結論

探究1如圖1，AB為⊙O的直徑，C為⊙O上一點，且 AD⊥CD，AC平分∠DAB，求證：CD是⊙O的切線.

分析聯(lián)結OC，要證明CD是⊙O的切線，只需證OC⊥CD.因為 AD⊥CD，所以只需證 OC∥AD，由 OA=OC和AC平分∠DAB，可證∠DAC=∠OCA，因此 OC∥AD.

探究2如圖1，AB為⊙O的直徑，C為⊙O上一點，過點C的切線交AD于D，AC平分∠DAB，證明：AD⊥CD.

分析聯(lián)結 OC，要證明 AD⊥CD，只需證∠DCA+∠DAC=90°.由于 CD是切線，因此∠DCO=∠DCA+∠ACO=90°，故只需證∠DAC=∠ACO，這可由OA=OC和AC平分∠DAB來證得.

探究3如圖1，若點A，B，C在⊙O上，AD和過點 C的切線互相垂直，垂足為 D，AC平分∠DAB，試說明：AB為⊙O直徑.

分析聯(lián)結OA，OC，要證明AB為⊙O直徑，只需證明點A，O，B共線，即證∠CAO=∠CAB.

綜上可知：在圖1中，由“AB為⊙O的直徑”、“CD是⊙O的切線”、“AC平分∠DAB”、“AD⊥CD”中任意3個作為條件都可以推出第4個成立.因此在中考復習時，適當?shù)慕粨Q題設與結論，形成新的命題，論證其成立與否的過程，其實就是對圖形本身和問題內(nèi)在聯(lián)系的再消化，有利于發(fā)展學生的思維，提高靈活運用知識解決問題的能力.

變形2延伸與拓展

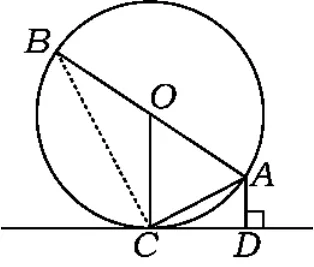
圖2

探究1如圖2，AB是⊙O的直徑，AC是弦，CD是⊙O的切線，C為切點，AD⊥CD，垂足為D，求證：

(1)∠AOC=2∠ACD;

(2)AC2=AB·AD.

分析(1)要證明∠AOC=2∠ACD，只需證明∠AOC=2(90°－∠ACO)，即證∠AOC=180°－2∠ACO.

(2)要證明AC2=AB·AD，即證，聯(lián)結BC，只需證明 Rt△ACD∽Rt△ABC.

探究2如圖3，已知AB是⊙O的直徑，AC為弦，且平分∠BAD，AD⊥CD，垂足為D.

(1)求證：CD是⊙O切線;

(2)若⊙O的直徑為4，AD=3，求∠BAC的度數(shù).

分析(1)同“變形1中的探究1”.

(2)聯(lián)結BC，在Rt△ABC中要求∠BAC的度數(shù)，因為AB=4，所以只需求出AC長，又已知AD=3，因此可通過Rt△ADC∽Rt△ACB來求解.

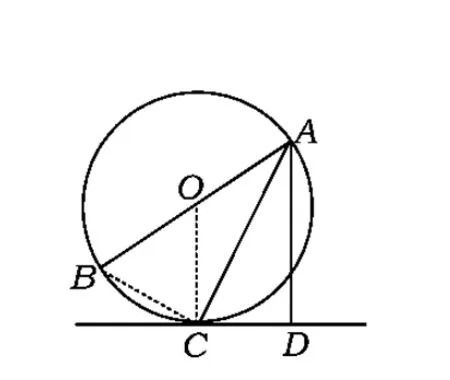
圖3

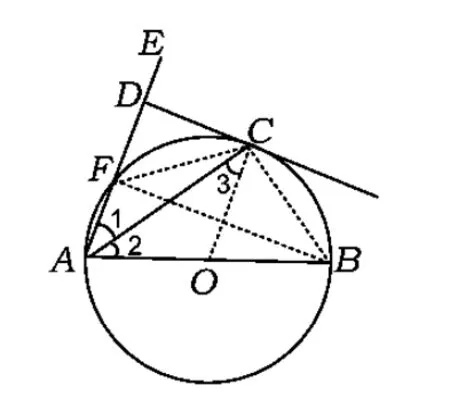
圖4

探究3如圖4，AB是⊙O的直徑，AE交⊙O于點F，且與⊙O的切線CD互相垂直，垂足為點D.

(1)求證：∠EAC=∠CAB.

(2)若 AD=8，CD=4，①求⊙O 半徑;②求tan∠BAE的值.

分析(1)同母題的解法.

(2)①聯(lián)結 BC，要求⊙O的半徑，只需證Rt△ACD∽Rt△ABC，由相似三角形的對應邊成比例，即可求得AB的長，繼而可得半徑.

②聯(lián)結CF與BF，要求tan∠BAE的值，只需求出AF，BF，為此需證明△DCF∽△DAC.

在母題背景下，不斷探尋圖形中有關邊、角乃至三角形間的數(shù)量關系或位置關系，通過分析學會在復雜圖形中尋找基本圖形，善于挖掘出條件中的隱含信息.當賦予邊或角一定的數(shù)值時，又把一般轉化為特殊，形成對基本知識點的再次理解鞏固，提升了數(shù)學能力!

由上述變形探索，我們會發(fā)現(xiàn)許多中考題都來源于教材，因此，在中考數(shù)學復習中，要依標扣本，抓基礎，保能力，要重視教材中的例題及習題的再研究、再加工，進行“一題多變”的探索和練習.通過適當?shù)难由旌屯卣梗治霾⒈容^它們的異同點，加深對本質(zhì)特征的認識，從而更有效地抓住問題的實質(zhì)，形成正確的觀點，更深刻地理解所學知識.通過精選的問題，精講精練，溝通各部分知識間的聯(lián)系，有效的形成知識網(wǎng)絡，拓寬解題思路，培養(yǎng)數(shù)學思維品質(zhì)，發(fā)展數(shù)學思維能力，在最終的復習過程中“以少勝多，以不變應萬變”，取得最佳的復習效果.