考慮應力狀態的HTPB/AP推進劑含損傷熱-粘彈性本構方程①

姚 東，張光喜，高 波

(1.第二炮兵工程大學，西安 710025;2.中國航天科技集團公司第四研究院，西安 710025)

考慮應力狀態的HTPB/AP推進劑含損傷熱-粘彈性本構方程①

姚 東1，張光喜2，高 波2

(1.第二炮兵工程大學，西安 710025;2.中國航天科技集團公司第四研究院，西安 710025)

從熱-粘彈性本構方程的一般形式出發，基于HTPB/AP推進劑單向拉伸應力應變曲線的多項式擬合，提出了細觀損傷的模量損傷效應函數;綜合考慮應力三軸度和Lode參數，引入應力狀態因子對損傷演化過程進行修正，建立了考慮應力狀態的HTPB/AP推進劑含損傷熱-粘彈性本構。對25℃、70 mm/min條件下單向、雙向應力試件拉伸過程的Abaqus有限元分析表明，與測試數據相比，單向、雙向加載應力-應變曲線初始上升段基本吻合、損傷效應體現的初始應變基本一致，在發展至斷裂延伸率附近時有明顯下降，整體規律與測試結果吻合較好;文中本構關系對應加載曲線的“脫濕”階段滯后測試數據約5%～6%應變(絕對值)，應力略高于測試數據，但相對誤差小于11%。

HTPB/AP推進劑;應力狀態;損傷效應函數;熱-粘彈性本構方程

0 引言

固體推進劑是以高分子網絡結構為基礎、混合大量含能組分的復合材料，具有高能量、高感度等性能特點和可澆注、易賦型等工藝特點。由于能量水平的提升，HTPB粘合劑體系的復合固體推進劑在導彈武器、航天運載等領域得到廣泛的應用［1］。

HTPB/AP推進劑的粘彈性力學行為與溫度、應變率和損傷程度、應力狀態等密切相關。圍繞溫度、應變率對其力學行為的影響，國內外學者相繼發展了蠕變型各向異性線粘彈性［2］等本構方程，同時形成了粘彈性力學應用體系，以Prony級數為代表的典型本構關系已經內嵌到Abaqus等商業軟件中。針對損傷的影響，Sook-Ying Ho發展了適用于高應變率的固體推進劑含損傷本構［3］;陽建紅通過熱氧老化實驗、聲發射損傷檢測實驗和蠕變柔量測試實驗，確定了HTPB復合固體推進劑老化損傷本構關系［4］;彭威等建立了考慮固體填料/粘合劑基體界面、微孔洞、微裂紋等細觀特征的幾何模型，結合平均化處理等方法獲得損傷變量及其演化信息［5］;趙玖玲通過推進劑單向拉伸和原位動態掃描電鏡觀測，研究了細觀損傷特征與推進劑初始模量、強度值的對應關系［6］。

相比之下，針對應力狀態對力學行為影響的研究報道較少。沙寶林對Sook-Ying Ho提出的模型進行了修正，引入壓力敏感系數考慮壓力的影響建立了含損傷的統一型本構模型［7］;該壓力敏感系數適用單一的內壓載荷，考慮了應力狀態的影響，但未給出具體的影響模式。

本文從熱-粘彈性本構方程的一般形式出發，基于單向拉伸應力應變曲線的多項式擬合建立損傷效應函數，同時引入應力狀態因子對損傷演化過程進行修正，建立了考慮應力狀態的復合固體推進劑含損傷熱-粘彈性本構，為固體火箭發動機的結構完整性與可靠性分析奠定了基礎。

1 損傷效應函數與熱-粘彈本構方程

1.1 含損傷熱-粘彈本構的一般形式

積分型熱-粘彈性本構方程可寫為

式中 E、ν分別為楊氏模量和泊松比，為獨立的材料參數。

唐雪松的研究指出［8］，受損材料的本構方程與無損時的形式相同，彈性常數由材料損傷后的有效值所取代，而不是按照應變等效假設用有效應力代替柯西應力，并進一步定義損傷效應函數描述材料常數隨細觀損傷的發展。本文定義標量損傷變量D，并進一步定義獨立材料參數E、ν對應的雙標量損傷效應函數:

1.2 HTPB/AP推進劑損傷效應函數的定義

損傷效應函數引入后，基于宏觀唯象描述的含損傷粘彈性本構的應用更為便捷。本文從宏觀加載的應力-應變曲線進行分析，定義損傷效應函數。圖1為某配方HTPB/AP推進劑標準試件的加載曲線。

圖1 某配方HTPB/AP推進劑標準試件的加載曲線Fig.1 Stress-strain curves of axial tensile for a HTPB/AP propellant

圖1所示應力-應變曲線可按5階多項式擬合:

綜合可得:

泊松比的損傷效應函數尚無法確定，本文暫不加以研究，假定 Mν(t)=1。

1.3 應力狀態的表征

為考察應力三軸度pσ、Mises應力σV、靜水壓力σe以及Lode參數μσ對應力狀態的表征有效性，取第一主應力σ1=1.0 MPa，并令第二、第三主應力滿足 σ1/σ2=1.0～2.0、σ3=-1.0～1.0，分別繪制了 pσ、σV隨 σ3的變化(見圖 2)，以及 σe、μσ隨 σ3的變化(見圖 3)。

圖 2 pσ、σV隨 σ3的變化Fig.2 pσ and σVchange with σ3

圖3 σe、μσ隨 σ3的變化Fig.3 σeand μσ change with σ3

在 σ1/σ2=1.0～2.0 條件下，圖 2、圖 3 表明:

(1)靜水壓力和Mises應力均隨σ3線性變化，而應力三軸度和Lode參數隨σ3呈非線性變化;

(2)不同 σ1/σ2比值下，靜水壓力、Mises應力、應力三軸度和Lode參數取值均出現周期，不具有唯一性。定義應力狀態修正無量綱因子f:

1.4 含損傷的粘彈本構

定義考慮應力狀態的損傷效應函數如下:

應力狀態因子f內含的材料常數F1、F2，模量損傷效應函數多項式擬合參數 B0、B1、B2、B3、B4、B5，以及損傷特征時刻tD、tF是新增的10個本構參數，其中獨立參數為9個。這9個獨立參數中，F1或F2需借助雙向應力試件拉伸測試加以確定，其余由單向測試數據擬合獲得。

2 單、雙向應力加載試驗的有限元分析

2.1 本構參數

選擇某配方HTPB/AP推進劑，見表1。

表1中，采用側粘式雙向試件(專利:一種固體推進劑、火藥雙向拉伸試件201218001811.5)進行雙向加載以求解F2，測試條件為20℃、100 mm/min。

2.2 拉伸試驗過程的有限元分析

單向應力試驗采用啞鈴型試件，見圖4;測試條件為25℃、70 mm/min。雙向試件采用側粘式雙向試件(專利:一種固體推進劑、火藥雙向拉伸試件201218001811.5)，測試條件為 25 ℃、70 mm/min。

圖5為單向試件實驗數據與有限元分析數據的曲線對比。圖6為雙向試件實驗數據與有限元分析數據的曲線對比。

表1 HTPB/AP推進劑本構參數Table 1 Parameters of constitutive equations for HTPB/AP propellant

表2 無損傷彈性模量的Prony級數參數Table 1 Parameters of Prony series for HTPB/AP propellant without damage

圖4 單向試件尺寸Fig.4 Size of axial tensile test sample

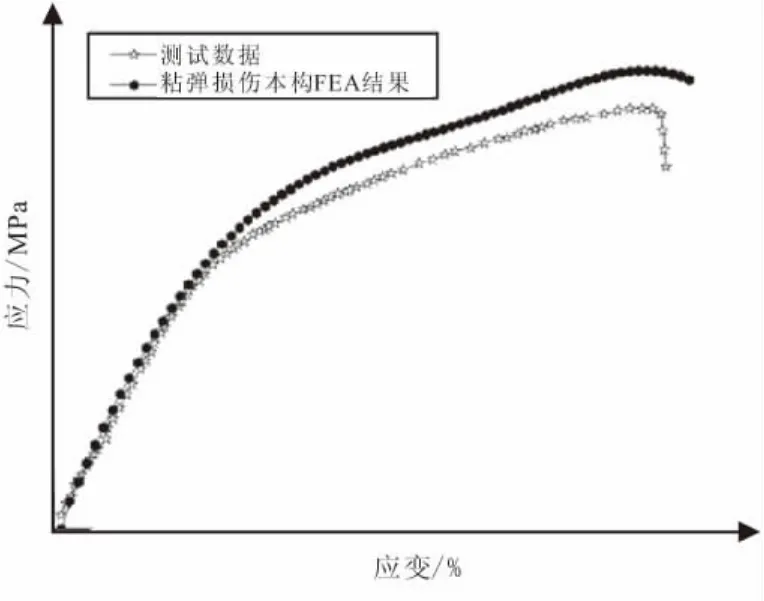
圖5 單向試件測試數據與FEA結果Fig.5 Stress-strain curves of test and FEA for axial tensile

圖6 雙向試件測試數據與FEA結果Fig.6 Stress-strain curves of test and FEA for biaxial tensile

對比結果表明:

(1)單向試件曲線初始上升段基本吻合、損傷效應體現的初始應變基本一致，但有限元分析的“脫濕”階段相對較寬，滯后約6%應變(絕對值);有限元分析應力高于測試數據(相對誤差6%～11%)，損傷效應函數的表達偏“軟”。

“脫濕”階段相對較寬、分析應力高于測試數據，是損傷本構對應曲線的整體趨勢。由于W-L-F方程的參數本身是松弛模量主曲線測試數據的擬合值，模量外推至其他條件時，必然存在與外推條件下實測數據的偏差;兩者的偏離程度和方向，取決于主曲線測試的誤差水平以及特定HTPB/AP推進劑配方體系性能的穩定水平。

(2)雙向試件有限元分析的曲線初始上升段與試驗規律基本一致，但呈現明顯的雙峰效應，即在“脫濕”階段完成后、應力達到斷裂強度前存在“平臺”。

導致該現象的原因，主要在于損傷效應函數由單向試件的加載曲線擬合獲得，一定應力狀態下，按指定因子修正后，與真實狀態的損傷效應存在差別。

(3)引入損傷效應函數后，材料參數矩陣維持了可逆、對稱等結構特點，有限元分析的結果曲線末尾均出現下降段，突破了以往彈塑性有限元分析中流動法則對曲線“只升不降”的限制。

3 結論

(1)與測試數據相比，單向、雙向加載應力-應變曲線初始上升段基本吻合，損傷效應體現的初始應變基本一致，整體規律與測試結果吻合較好。

(2)本文本構關系對應加載曲線的“脫濕”階段滯后測試數據約5%～6%應變(絕對值)，應力略高于測試數據，但相對誤差小于11%。

致謝:

本研究工作受到中國航天科技集團公司第四研究院第十一批青年科技基金資助，四院四十一所史宏斌博士指導了研究工作的開展，就損傷引入型式、本構模型工程化應用拓展等提出了寶貴建議。中國航天科技集團公司第四研究院四十一所沙寶林博士在Abaqus下UMAT計算收斂問題、Abaqus北京代表處龔平博士在基于Python的Abaqus后處理等技術問題上給予了悉心幫助，在此一并致謝。

［1］侯林法.復合固體推進劑［M］.北京:宇航出版社，1994.

［2］鄧偉，楊挺青.基于內變量理論的一種廣義粘彈性本構方程［J］.固體力學學報，1997，18(1):11-16.

［3］Sook-Ying Ho.High strain-rate constitutive models for solid rocket propellants［J］.Journal of Propulsion and Powers，2002，18(5):1106-1111.

［4］陽建紅，俞茂宏，侯根良，等.HTPB復合固體推進劑含損傷和老化本構研究［J］.推進技術，2002，23(6):509-512.

［5］彭威，任均國，周建平.復合固體推進劑非線性粘彈本構方程的細觀力學分析［J］.固體火箭技術，1999，22(4):23-26.

［6］趙玖玲，強洪夫.MAPO含量和AP級配對丁羥推進劑力學性能的影響［J］.固體火箭技術，2011，34(3):329-334.

［7］沙寶林，侯曉.壓力環境下固體推進劑含損傷的統一本構研究［J］.強度與環境，2012，39(3):13-18.

［8］唐雪松，蔣持平，鄭健龍.各向同性彈性損傷本構方程的一般形式［J］.應用數學和力學，2001，22(12):1317-1323.

(編輯:崔賢彬)

Constitutive equations involving damage for HTPB/AP propellant considering stress state

YAO Dong1，ZHANG Guang-xi2，GAO Bo2
(1.The second Artillery Technical University of PLA，Xi’an 710025，China;2.The Fourth Academy of CASC，Xi’an 710025，China)

Based on general expression of thermal-viscoelastic constitutive equation，damage effect function of propellant Young’s modulus was formulated by fitting axial tensile stress-strain curves in forms of 5-order polynomials.Then stress triaxiality as well as Lode parameter was introduced to conceive stress field factor，with the purpose to modify the damage effect.Ultimately，constitutive equations involving damage for HTPB/AP propellant was established.Finite element analysis(FEA)on axial and biaxial tensile on the condition of(25℃，70 mm/min)indicates that curves of FEA data are similar to testing results for both axial and biaxial tensile specimen，curves of FEA data shows decline when rupture is nearby，and the maximum relative error of stress is 11%.

HTPB/AP propellant;stress state;damage effect function;thermal-viscoelastical constitutive equations

V435+.21

A

1006-2793(2014)04-0496-04

10.7673/j.issn.1006-2793.2014.04.012

2013-09-11;

2014-04-27。

中國航天科技集團公司第四研究院第十一批青年科技基金資助。

姚東(1982—)，男，博士生，研究方向為固體火箭發動機藥柱失效分析與性能表征。