變質量貯箱類流固耦合系統的振動響應及時頻特性分析
馬馳騁, 張希農,柳征勇,胡迪科
(1.西安交通大學 機械結構強度與振動國家重點實驗室,西安 710049;2.上海宇航系統工程研究所,上海 201108)
隨著對火箭運載性能要求的提高,火箭推進劑所占結構的比重不斷增大,液體燃料與燃料貯箱的耦合振動對于火箭正常運行的影響越來越大。由于火箭攜帶的燃料質量大,整體結構頻率比較低。而且隨著燃料的消耗,系統的總體質量減少,將引起系統振動頻率的顯著改變,液體燃料消耗對火箭的運動有著顯著的影響。另外,研究液體燃料與貯箱結構之間的流固耦合振動,對于火箭飛行性能與飛行安全也有著重要的意義。燃料貯箱在火箭飛行過程中會受到主發動機強烈的振動和沖擊影響,除了受到外界載荷的影響外,內部填充的液體燃料也會產生晃蕩作用,從而產生外界載荷與內部流固耦合作用共同疊加的效應。近年來,貯箱的動力學研究得到許多航天工作者的重視。許多學者完成了充液容器晃動問題的開創性研究工作,Moiseevp[1]詳述了有關充液容器晃動問題的基本理論和文獻。Ibrahim等[2]在綜述性文章中介紹了關于含液體晃動系統的動力學研究方法及研究進展。國內很多學者針對含液容器中液體的晃動影響也進行了一系列的研究。周思達等[3]介紹了近年來運載火箭貯箱流固耦合系統的分析方法。茍興平等[4]利用推廣形式的駐定壓力原理建立了剛-液耦合系統液體晃動的動力學方程,并研究了其動力學特性。包光偉[5]以油罐車為背景,建立了平放柱形貯箱內液體晃動的等效力學模型。劉文一等[6]研究了在升空過程中振動沖擊對某姿控發動機雙層結構燃料貯箱的影響,利用流固耦合理論,對空載和充液兩種條件下的貯箱進行了模態分析、頻率響應分析和沖擊響應分析。朱琳等[7]將表征液體運動的節點壓力縮聚到自由面,利用主坐標表征液體晃動,采用等效Laplace方程的邊值問題求解了液固耦合方程組中的附加質量矩陣、附加剛度矩陣和耦合矩陣,分析并獲得了推進劑及貯箱的液固耦合振動特性。但是以往的研究者主要研究了液體晃動對系統響應的影響,關于液體減少過程中貯箱的動力學分析的問題開展的較少。
本文中,重點研究了變質量貯箱流固耦合系統的動力學建模及動力學響應分析。考慮到系統的復雜性,采用PATRAN-NASTRAN有限元程序和動力學響應分析的Newmark直接積分法,建立了變質量貯箱流固耦合有限元模型并得到了其響應,并使用SPWVD研究了變質量系統的時頻特性。通過比較不同條件下貯箱結構的動力學響應,重點觀察了變化的質量對該燃料貯箱的影響。本文提出的建模及動力學仿真方法,可用于處理類似的變質量結構的動力學問題。

圖1 含液貯箱示意圖Fig.1 A fluid containing tank
1 運動方程
所考察的彈性貯箱動力學模型如圖1所示,圓柱形貯箱半徑為R,高度為H,充液深度為h(t),是一個隨時間減小的函數。假設液體為無粘、無旋、不可壓縮的理想流體,則其運動的速度場有勢。
針對貯液箱中液體與箱體彈性結構相互作用的復雜性,而現在又面臨的變質量的問題,更增加了該流固耦合系統動力分析問題的困難性。為解決該問題,必須對該問題的模型進行簡化。其中解決該問題的一種有效的簡化方法就是虛擬質量法,即將流體對固體的作用,以固體的附加質量的形式出現。該方法可以有效的化簡流固耦合問題,極大的減小工作量,是處理貯液箱問題的一種有效手段。在流固耦合系統中。使用虛擬質量法,通過施加一個附加質量矩陣實現不可壓縮流體對結構的作用,考慮流體作用時系統的有限元計算方程[8]為:
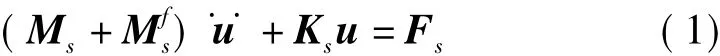
其中Ms和Ks分別為殼體結構的質量矩陣和剛度矩陣,Fs為外載荷矩陣,u和分別為位移向量和加速度向量代表流體對固體的作用,現以結構的附加質量的形式出現,稱為附加質量矩陣。流固耦合問題退化為考慮附加質量的固體動力學問題,從而大大簡化了流固耦合系統的分析。
基于附加質量理論,NASTRAN采用邊界元法得到附加質量矩陣,并稱之為虛擬質量法,對于不可壓縮、忽略表面自由表面波動的非粘性流體,流體力學的基本方程可以簡化為Laplace方程。用Helmholtz邊界積分法求解Laplace方程,可以得到流體邊界上任意一點ri處的速度向量和壓力向量分別為:

其中σj為流場在點rj處面元Aj上的流體通量,eij為從點j到i的單位向量。ρ為流體的密度。對式(2-3)在結構有限元表面進行積分,得到:

其中矩陣[χ]和[Λ]為積分系數矩陣,F為流體作用在結構上的節點力。同時根據力向量、質量矩陣和加速度向量的關系:

通過式(7),將流體對固體的作用,以固體的附加質量的形式出現。由于一般情況下,水對結構的形成的剛度相對于結構本身的剛度小得多,因此可以忽略,從而得到貯箱結構的動力學方程如式(1)所示。
虛擬質量法避免了流體單元網格的劃分,大大簡化了建模過程,有利于工程應用。燃料沒有消耗即系統的質量不發生改變時,系統的動能和彈性勢能可以表示為

在飛行器飛行當中,燃料的消耗使得附加質量是一個隨時間變化的函數,因此當系統的質量變化時,系統的動能可以寫為

假設系統的結構阻尼是質量矩陣和剛度矩陣的線性組合,即Rayleigh阻尼:

Rayleigh阻尼的比例系數α和β可以根據系統的前二階橫向振動固有頻率和模態阻尼比求得。

2 數值仿真
這里采用的模型為一個兩端封閉的圓柱殼,使用有限元軟件PATRAN-NASTRAN,采用虛擬質量法,對圖1所示的貯箱建立有限元模型如圖2所示。殼體底面半徑為0.2 m,殼體厚度為0.004 m,高度為1 m。有限元網格如下圖2所示,共有462個節點和460單元。假設固體結構材料為各項同性材料,彈性模量為71 GPa,泊松比為 0.33,密度為 2 850 kg/m3,貯箱內液體的密度為1 000 kg/m3。支撐彈簧采用BUSH兩節點單元,殼體結構采用QUAD4四節點單元。在PATRANNASTRAN虛擬質量法中,在卡片ELIST中定義流固耦合作用面,通過卡片MFLUID定義不可壓縮流體的屬性,并將液體以附加質量的形式對結構的作用。只有在ELIST/MFLUID卡片中定義的單元才能輸出壓力,附加質量矩陣的變化隨著ELIST/MFLUID卡片中定義的單元的變化而變化。
對節點342處施加一個初始外力,產生一個初始位移,撤去外力后,研究結構的自由振動。在研究當中,只給了系統一個初始的位移,形狀與左右擺動振形相似(充滿液體時第1階振形)。圖3中給出了建模及仿真分析流程圖。其中計算的難點在于構建變質量系統的質量變化函數,由于在計算迭代過程中涉及到變化的質量矩陣和剛度矩陣,計算量比較大,耗時長。使用有限元軟件NASTRAN得到系統 t1,t2,t3,…時刻的質量矩陣和剛度矩陣后,采用線性插值的方法得到系統t時刻的質量矩陣和剛度矩陣,使用Newmark直接積分法計算了系統的位移響應,然后使用快速Fourier變換得到了系統的頻率響應曲線。

圖2 有限元網格Fig.2 Finite element model of a fluid containing tank

圖3 計算流程圖Fig.3 The flow chart of the calculation
首先計算了不同液面高度時系統的第一階橫向振動固有頻率。第一階橫向振動固有頻率隨殼體中液面高度的變化曲線如圖4所示。使用虛擬質量法,在PATRAN-NATRAN中直接計算得到系統的固有頻率,如圖4中紅色線(三角形標記)所示,然后根據PATRAN-NATRAN中提取出的附加質量矩陣,在MATLAB程序中采用插值的方法計算任意時刻系統的固有頻率,如圖4中藍色線(圓形形標記)所示。使用PATRAN-NATRAN求解時不變系統的固有頻率非常方便,但是處理質量時變系統的瞬態響應比較困難。編寫MATLAB程序對PATRAN-NATRAN進行二次開發,是一種簡單有效的方法。在飛行器飛行過程中,隨著燃料的消耗,貯箱結構的質量減少,但是剛度基本不受影響,因此系統的振動頻率會隨之增大。第一階橫向振動固有頻率從10.171 Hz增大到 34.879 Hz。通過NASTRAN計算得到的結果和編制的MATLAB程序計算得到的結果比較一致,說明了程序的有效性。
前二階模態阻尼比在這里分別取為0.58%和0.41%。根據貯箱空箱時的固有頻率,可以求得Rayleigh阻尼系數 α =2.180 2,β =7.537 1 ×10-6,當貯箱中裝滿燃料時,根據系統的固有頻率可以求得Rayleigh阻尼系數 α =0.67,β =1.732 ×10-5。計算表明,滿箱時系統的結構阻尼比空箱時系統的結構阻尼大,因此計算中使用了滿箱時系統的結構阻尼比例系數。圖5和圖6分別給出了系統的自由振動位移響應曲線和振動響應曲線。對比情況1和情況2兩種情況下系統的位移響應和頻率響應,可以看出,變質量引起的負阻尼對系統的影響非常顯著,極大的減緩了系統振動的衰減。特別是在1 s-3.5 s之間,系統的質量變化引起的負阻尼對系統的影響尤為顯著。由于系統的質量是變化的,所以系統的振動頻率也是隨時間變化的。在頻譜圖上,可以明顯看出,與時不變系統不同的是,質量時變系統的頻響曲線是由一系列的頻率值組成的,振動頻率的變化范圍與圖4中所示的系統的變化范圍是一致的,也就是說系統的振動頻率的變化范圍,可以根據系統質量的變化范圍確定。

圖4 不同液面高度時系統的第一階橫向振動固有頻率Fig.4 Lateral vibration frequency of first order for different liquid level height

圖5 節點342處x方向的位移響應Fig.5 Displacement responses of Node 342 in x direction

圖6 節點342處x方向的頻率響應Fig.6 Frequency responses of Node 342 in x direction

圖7 節點342處x方向的位移響應Fig.7 Displacement responses of Node 342 in x direction
從式(6)中可以看出,變質量引起的阻尼與質量變化率成正比,如果系統的質量迅速減小,那么會產生一個比較大的負阻尼。圖5和圖6分別給出了系統的自由振動位移響應曲線和頻率響應曲線。這里假設系統的質量變化過程只有1 s,在系統的振動中,變化的質量引起了一個非常大的負阻尼。從位移響應曲線和頻率響應曲線可以明顯看出,t<0.7 s時,負阻尼的使得系統的振幅增大,當t>0.7 s,結構阻尼的作用大于負阻尼的作用,使得系統的振幅衰減。從頻響曲線中也可以看出負阻尼使系統的振動振幅增大。
3 時頻特性分析
從上面的分析中可以發現,Fourier變換缺乏時間和頻率的定位功能,在分辨率上以及對非平穩信號分析具有局限性。而Wigner-Ville分布憑借其優良的時變特性和較高的時頻分辨率一直被應用于信號的分析和處理領域。Wigner-Ville分布是Cohen類分布的一種[9-10],是一種雙線性的表示時頻分布的函數。所謂雙線性形式,是指所研究的信號在時頻分布的數學表達式中以相乘的形式出現兩次。Wigner于1932年首先提出Wigner分布的概念,并把它用于量子力學領域。在之后的一段時間內并沒有引起人們的重視。直到1948年,首先由 Ville把它應用于信號分析。因此,Wigner分布又稱Wigner-Ville分布,簡稱為WVD。其表達式如下:

圖8 節點342處x方向的頻率響應Fig.8 Frequency responses of Node 342 in x direction

x(t)和X(ω)分別為真實的時域信號和頻域信號。*表示函數的復共軛函數。從式中可以看到,由于WVD可以在整個時-頻域顯示信號的能量分布。Wigner-Ville分布實質上是對信號的瞬時相關函數的Fourier變換,其結果能夠反映信號的時頻特征。為了減少交叉項,平滑偽Wigner-Ville分布(SPWVD)對時域變量和頻域變量同時加窗。其定義為:

這里的W(ω-η)和g(t-τ)是兩個實對稱窗口。對信號進行時域頻域加窗平滑處理后,時域和頻域上的交叉項可以得到很大的抑制。而且時域平滑和頻域平滑的尺度容易控制,并且可以獨立選擇窗函數W(ω-η)和 g(t-τ)的長度[11]。
首先研究了系統質量變化率比較小時的時頻響應。對圖5中的位移響應曲線做SPWVD,得到了圖9和圖10中顯示的兩種情況下節點342處x方向位移的時頻響應譜。從圖中可以看出任意時間任意頻率點系統的振動能量密度。圖11和圖12給出了系統的系統振動頻率隨時間的變化譜圖,與圖2中系統的頻率變化曲線是一致的,這是傳統的FFT變換無法得到的。

圖9 節點342處x方向位移的時頻響應譜Fig.9 SPWVD of the displacement of Node 342 in x direction

圖10 節點342處x方向位移的時頻響應譜Fig.10 SPWVD of the displacement of Node 342 in x direction
類似的,對圖7中的位移響應曲線做SPWVD,得到了圖13和圖14中顯示的兩種情況下節點342處x方向位移的時頻響應譜。對比圖13和圖14可以看出,當考慮負阻尼的作用時,由于負阻尼的作用超于過了系統結構阻尼的作用,使系統的能量增大,從圖14中可以看出,系統的結構阻尼在振動中起主要作用,系統的能量隨時間減小。圖15和圖16給出了系統的系統振動頻率隨時間的變化譜圖。

圖11 節點342處x方向位移的時頻響應譜Fig.11 SPWVD of the displacement of Node 342 in x direction

圖12 節點342處x方向位移的時頻響應譜Fig.12 SPWVD of the displacement of Node 342 in x direction

圖13 節點342處x方向位移的時頻響應譜Fig.13 SPWVD of the displacement of Node 342 in x direction

圖14 節點342處x方向位移的時頻響應譜Fig.14 SPWVD of the displacement of Node 342 in x direction

圖15 節點342處x方向位移的時頻響應譜Fig.15 SPWVD of the displacement of Node 342 in x direction

圖16 節點342處x方向位移的時頻響應譜Fig.16 SPWVD of the displacement of Node 342 in x direction
4 結論
基于虛擬質量法,推導了變質量貯箱流固耦合系統的有限元方程,使用NASTRAN-MATLAB建立了變質量儲箱的有限元模型,該模型主要考慮了系統的質量變化對系統動力學特性的影響。通過一個附加質量矩陣來表征流體對固體結構的影響,大大簡化了建模及數值仿真。有限元方程的解與NASTRAN計算的結果是一致的,說明了這種方法的可行性。
(1)附加質量矩陣與流體的液面高度有很大的關系。由于系統的質量是隨時間變化的,因此系統的振動頻率也是隨時間變化的。振動頻率的變化范圍可以通過系統質量的變化范圍確定。
(2)變化的質量對系統的另外一個影響主要體現在產生了一個附加的阻尼。變質量引起的阻尼與系統的質量變化率有直接的關系,也就是說,系統質量變化越快,產生的負阻尼越大。當系統質量增加時,會產生一個正阻尼,而當系統質量減少時,會產生一個負阻尼。特別需要注意的是,當產生的負阻尼的作用超過了系統本身結構阻尼的作用時,會引起系統振幅的增大。如果變形超出了結構的彈性范圍,甚至會造成系統的破壞。
(3)使用Wigner-Ville分布變質量貯箱流固耦合系統的振動信號進行分析,獲得了振動信號的時頻響應譜。在時頻域上研究了非穩態信號的時頻特性,通過時頻譜圖上的能量密度分布,可以觀察系統在特定時間特定頻率時的振動特性。Wigner-Ville分布是分析非穩態信號的一種有效工具。
[1]Moiseev N N.Introduction to the theory of oscillations of liquid-containing bodies[J]. Advances in Applied Mechanics,1964,8:233 -289.
[2]Ibrahim R A,Pilipchuk V N,Ikeda T.Recent advances in liquid sloshing dynamics[J].Applied Mechanics Review,2001,54(2):133-199.
[3]周思達,劉莉.運載火箭貯箱流固耦合分析方法綜述[J].強度與環境,2010,37(3):52 -63.ZHOU Si-da,LIU Li.A review on the analysis methods of fluid-structure coupling for launch vehicle fuel tank[J].Structure & Environment Engineering,2010,37(3):52-63.
[4]茍興宇,尹立中,馬興瑞,等.窄長方形貯箱中液體的強迫晃動[J].力學與實踐,1998,20(4):20-22.GOU Xing-yu,YIN Li-zhong,MA Xiong-rui,et al.Forced sloshing of liquid in a narrow rectangular container[J].Mechanics in Engineering,1998,20(4):20 -22.
[5]包光偉.平放柱形貯箱內液體晃動的等效力學模型[J].上海交通大學學報,2003,37(12):1961 -1968.BAO Guang-wei,Equivalent mechanical model of liquid sloshing in horizontal cylindrical container[J].Journal of Shanghai Jiaotong University,2003,37(12):1961 -1968.
[6]劉文一,李玉龍,吳訓濤,等.流固耦合作用下某雙層結構燃料貯箱動力學特性分析[J].彈箭與制導學報,2011,31(5):132-134.LIU Wen-yi,LI Yu-long,WU Xun-tao,et al.Analysis of dynamic characteristic of double-deck propellant tank under liquid-solid coupling interaction[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(5):132 -134.
[7]朱琳,唐國安,柳征勇,等.推進劑與貯箱液固耦合振動的動力學分析[J].振動與沖擊,2012,31(5):139-143.ZHU Lin,TANG Guo-an,LIU Zheng-yong,et al.Dynamic analysis for fluid-structure coupled vibration of propellants and fuel tank[J].Journal Vibration and Shock,2012,31(5):139-143.
[8] MSC.Nastran advanced dynamic analysis user’s guide[M].Santa Ana.CA 92707 USA:MSC.Software Corporation,2004.
[9] Cohen L.Time-frequency distributions-A review[C].Proc.IEEE,NY USA,1989,77(7):941 - 981.
[10] Hlaswatch F,Boudreaux-bartels G F.Linear and quadratic time-frequency signal representations[J]. IEEE Signal Processing Magazine,1992,4:21 -67.
[11]姜鳴,陳進,汪慰軍.幾種Cohen類時頻分布的比較及應用[J].機械工程學報,2003,39(8):129-134.JIANG Ming,CHEN Jin,WANG Wei-jun.Comparison and application of some time frequency distribution belonging to cohen class[J].Chinese Journal of Mechanical Engineering,2003,39(8):129-134.

