展向剪切流作用下斜置圓柱氣動特性研究

杜曉慶，費陳杰，況中華，趙 燕

(上海大學 土木工程系，上海 200072)

圓柱繞流是一個經典的流體力學問題，具有極為重要的研究意義和應用價值。在過去一個世紀內，雖然對這個問題已取得了大量研究成果［1］，但某些特定條件下的圓柱繞流問題仍需要進一步的研究。文獻［2－8］對均勻流作用下的斜圓柱繞流問題進行了研究，而文獻［9－14］研究了展向剪切流作用下直立圓柱的繞流特性。目前尚未見到研究展向剪切流作用下的斜置圓柱繞流的成果。

在很多實際工程中，如懸索橋主纜、斜拉橋拉索、桅桿拉索、海洋工程中的管道和錨纜等圓柱形結構，流體并非垂直作用于圓柱。并且來流也很少以均勻流的形式出現，在大氣邊界層和海底邊界層內均存在相當大的剪切作用，局部地貌也會增加來流的不均勻性。因此，對展向剪切流作用下的斜置圓柱繞流問題進行研究，具有研究和工程意義。

研究人員通過試驗方法［2－5］和計算流體力學方法(CFD)［6－8］對均勻流作用下斜置圓柱的繞流問題進行了研究。研究發現:沿斜置圓柱軸線方向的流體速度與垂直于圓柱截面方向的流體速度具有相同的量級［5，7－8］。Mastumoto 等［5］認為沿圓柱軸向方向的流體運動(或稱為軸向流)會干擾并減弱卡門渦強度。

對于剪切流垂直作用于直立圓柱的繞流問題，研究者一般也是通過試驗方法［9－11］和 CFD 方法［12－14］進行研究。研究發現:在展向剪切流作用下，圓柱展向會產生傾斜的胞狀旋渦脫落［9，14］。

本文針對展向剪切流作用下的斜置圓柱繞流問題，采用大渦模擬(LES)方法，在雷諾數為3 900時(雷諾數根據平均來流速度和圓柱直徑計算得到)，研究了來流與圓柱軸向夾角為45°的斜置圓柱在均勻流和兩種不同強度展向剪切流作用下，斜置圓柱的表面風壓分布、Strouhal數、氣動力功率譜和相關性等氣動性能，并探討了剪切流的作用機理。

1 計算模型

1.1 坐標系及測點布置

坐標系和圓柱傾角定義如圖1所示，圖中α為圓柱傾角，D為圓柱直徑，L為圓柱長度，U為來流速度，Uo為來流在垂直于圓柱軸線方向的速度分量，Ua為來流在沿圓柱軸線方向的速度分量。圖中XYZ為整體坐標，xyz為圓柱軸截面局部坐標，其中Y軸和y軸都垂直于平面向內。

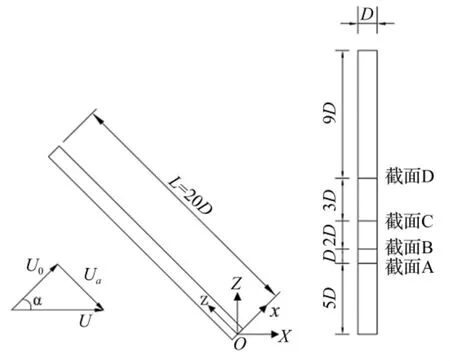
圖1 坐標系及測壓截面Fig.1 Coordinates and pressure measuring sections

在本文中，圓柱長度L為20D，斜置圓柱的傾角α為45°。為了與直立圓柱進行比較，本文還考慮了α為0°的直立圓柱在均勻流和剪切流作用下情況。為了降低計算工作量，計算雷諾數取為3 900(雷諾數根據平均來流速度U和圓柱直徑D計算得到)。無量綱的時間步長為 Δt*=0.02(Δt*=UΔt/D)。

沿圓柱展向(即圓柱軸線方向)布置了4個測壓截面(見圖1)，每個截面沿圓柱周向均勻布置32個壓力測點，在計算結果穩定可靠后開始采集數據。在本文中，除特別注明外，文中結果均來自B截面計算數據。

1.2 剪切流定義

展向線性剪切流指來流沿圓柱高度是線性均勻變化的如圖2所示，風速沿著整體坐標系的Z軸方向線性增大。剪切流的強度可用剪切系數k來表示，k=AD/(其中 A= U/Z，D 為圓柱直徑，為來流平均速度，見圖2所示)。在本文中，剪切系數k取為0(即均勻流)、0.02 和 0.05。

圖2 展向剪切流定義Fig.2 Definition of span-wise shear flow

1.3 氣動力定義

圓柱表面的氣動力系數CD、CL定義如下，方向如圖3所示:

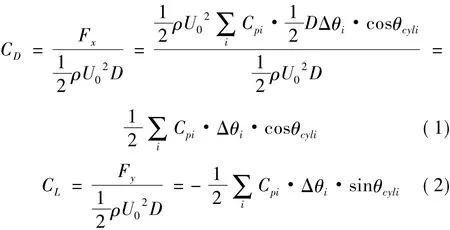
式中:ρ為空氣密度;Fx和Fy為作用在單位長圓柱模型上的x和y方向的氣動力，Cpi為圓柱表面第i個測點的風壓系數;Δθi為測點i和i+1之間交角;θcyli為第i個測點的位置角。

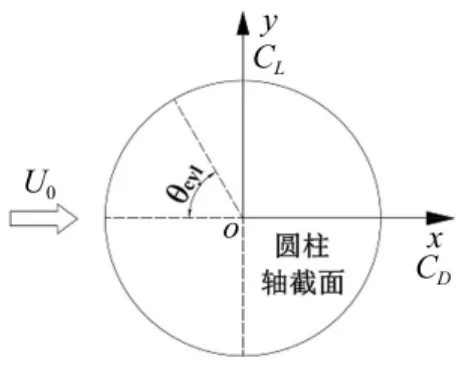
圖3 氣動力系數定義Fig.3 Definition of aerodynamic forces

2 計算方法

2.1 控制方程和亞格子模型

大渦模擬(LES)方法中，大尺度渦通過濾波后的Navier-Stokes方程直接求解，小尺度的渦則采用亞格子尺度模型(SGS)模擬。與雷諾平均法(RANS)相比，大渦模擬方法可更好地模擬流場中的湍流漩渦，能捕捉到豐富的流場脈動信息。而與直接數值模擬(DNS)相比，大渦模擬又能節省很大的計算量。本文采用Fluent軟件的大渦模擬湍流模型進行數值分析。

經過濾波函數的濾波，可得到大尺度渦的不可壓縮Navier-Stokes方程:

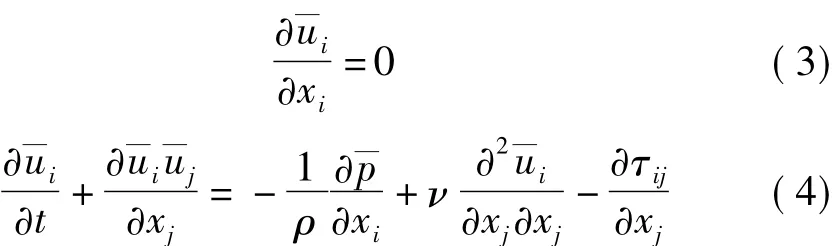
式中:為濾波后速度分量;ρ為流體密度;p—濾波后壓力;ν為流體動力粘度;τij為亞格子應力張量。

亞格子應力τij采用Smagorinsky-Lilly的亞格子尺度模型，具有以下形式:

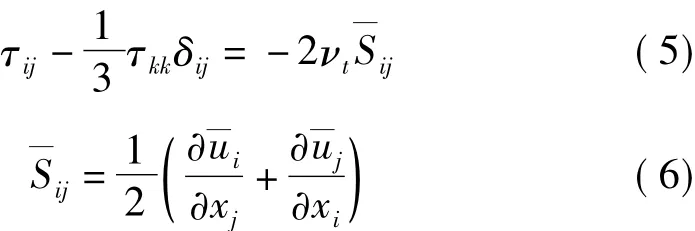
式中，νt是亞格子尺度的湍動粘度，為:

式中，Δi代表沿坐標軸i方向的網格尺寸，Cs是Smagorinsky常數，本文取0.1。

2.2 計算域和邊界條件

計算域為:長度×寬度×展向=30 D×20 D×20 D，詳見圖4。網格類型為六面體網格，圓柱周向均勻布置128個點，沿圓柱展向間距為0.1D，模型最小網格4 ×10－4D，最大網格為 1.05 D，總網格數量約為200萬。

計算域的邊界條件如下:進口采用速度邊界條件;出口采用出流邊界條件;圓柱上下面采用自由滑移壁面條件;圓柱展向端部采用對稱邊界條件;圓柱表面采用無滑移壁面條件。

圖4 平面網格及計算域Fig.4 Computational domain and grids

3 計算結果分析

3.1 計算結果驗證

為了驗證本文計算結果和計算方法的正確性和適用性，將本文直立圓柱的平均阻力系數和Strouhal數(St)與文獻［15］的大渦模擬結果和文獻［16］的風洞試驗結果進行了比較，結果列于表1內。從表1可見，本文的圓柱展向長度與文獻［16］的風洞試驗模型相似;而三者的雷諾數相近，均在亞臨界區內。從數值上看，本文的計算結果與其他研究者的結果相近，但平均阻力系數稍偏大而St數偏小。這種偏差可能是由于本文的計算條件和文獻［15］的計算參數以及文獻［16］的風洞試驗條件的差異所造成的。Zdravkovich［1］指出圓柱繞流對圓柱的表面粗糙度、來流湍流度、雷諾數、模型長度和阻塞率等條件非常敏感。因此，從總體上看，本文的計算結果是正確的，本文所采用的計算方法是合適的。

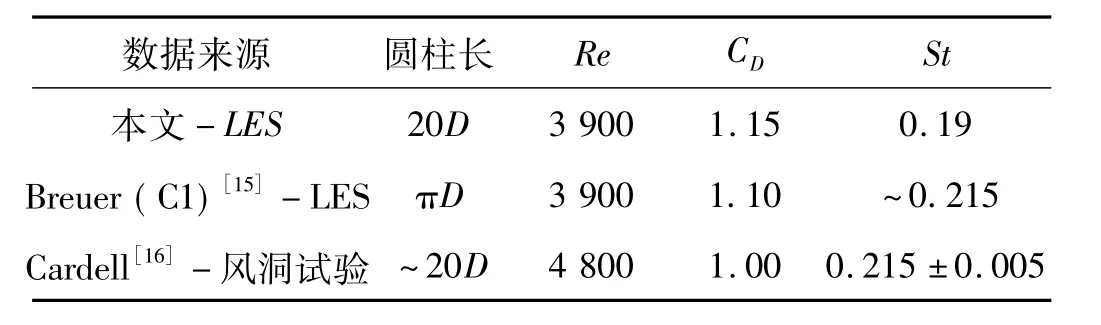
表1 直立圓柱的計算結果比較Tab.1 Comparison of results of non-inclined cylinders

3.2 風壓系數分布

圖5為傾角α為45°的斜置圓柱分別在均勻流(k為0)和兩種不同剪切流(k為0.02和0.05)作用下的平均風壓系數和脈動風壓系數(RMS)，圖中橫坐標為從停滯點開始的測壓點角度(角度定義見圖3)。為了進行比較，圖中也列出了直立圓柱(α為0°)在均勻流作用下的計算結果。風壓系數的計算均采用測壓截面處垂直于圓柱軸線方向的來流風速分量Uo。

由圖5(a)可見，對于均勻流作用下的圓柱，當傾角從0°增大為45°時，圓柱表面最大平均負壓以及平均基底風壓的絕對值均減小。有趣的是:對于傾角為45°的斜置圓柱，最大平均負壓和平均基底風壓的絕對值又隨著剪切系數的增大而逐漸增大;在k為0.05的剪切流作用下，斜置圓柱表面的平均風壓系數與均勻流作用下直立圓柱的表面風壓系數非常接近。

對于圓柱表面的脈動風壓系數(見圖5(b))，在均勻流作用下，斜置圓柱表面的脈動風壓系數要比直立圓柱小。這可能是由于斜置圓柱受到尾流區軸向流的影響，從而導致卡門渦脫強度降低所造成的。斜置圓柱脈動風壓系數隨剪切系數的變化規律與平均風壓相似:隨著剪切系數的增大，斜圓柱的脈動風壓系數逐漸增大并接近直立圓柱的情況。

3.3 Strouhal數沿展向變化

圖6為直立和斜置圓柱在剪切流作用下的Strouhal數(St)沿圓柱展向的變化規律。圖中縱坐標(z/D)為展向高度與圓柱直徑的比值。Strouhal數定義為:St=fD/，為來流平均風速，f為卡門渦脫頻率。

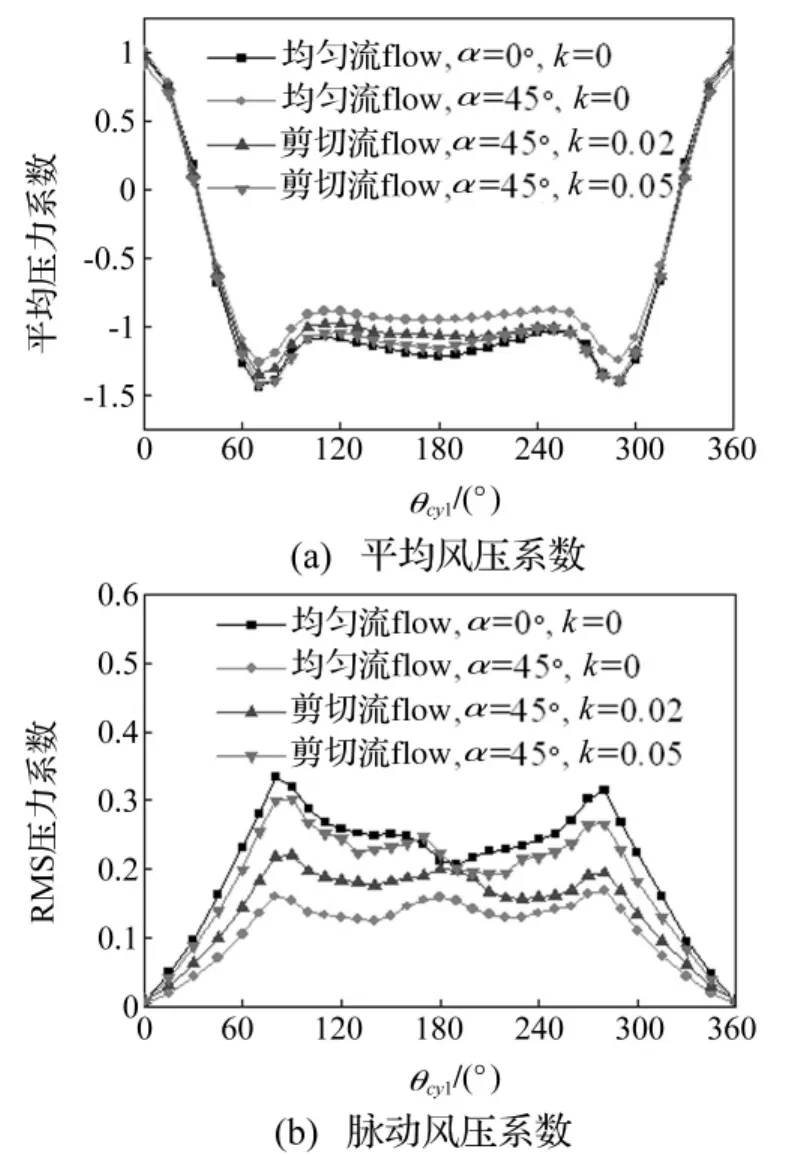
圖5 傾角和剪切系數對風壓系數的影響Fig.5 The effects of inclined angle and shear parameters on wind pressure coefficients

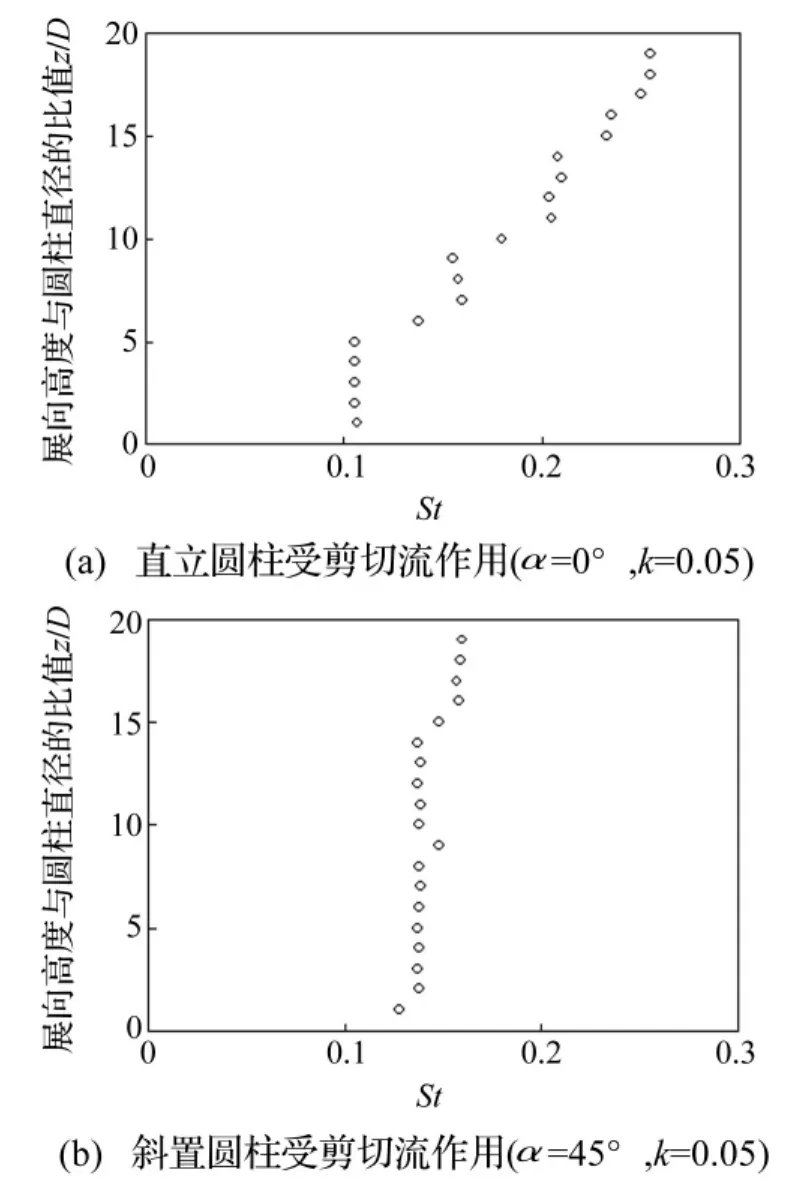
圖6 Strouhal數沿展向的變化Fig.6 The change of Strouhal numbers along span-wise

由圖6(a)可得，對于直立圓柱體，在剪切流作用下，St沿著圓柱展向發生明顯的變化，并且可以明顯觀察到在一定長度范圍內存在St鎖定的現象，即沿著展向形成所謂的胞狀渦，這與文獻［9，13］中所得結論基本一致。然后，對于剪切流作用下的斜置圓柱體，除了在圓柱上端外，St沿著展向沒有觀察到明顯的變化，見圖6(b)。這說明在斜圓柱尾流區形成的軸向流會破壞胞狀渦的形成。

3.4 氣動力系數

圖7為直立和斜置圓柱在均勻流和剪切流作用下的氣動力系數時程曲線。氣動力系數根據式(1)和(2)計算得到。

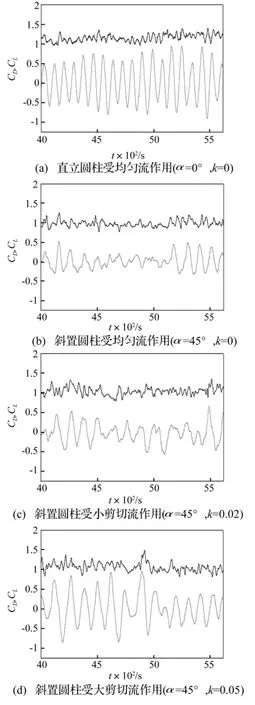
圖7 傾角和剪切系數對氣動力時程的影響Fig.7 Effects of inclined angle and shear parameter on time history of aerodynamic forces

由圖7可得，均勻流作用下，直立圓柱的平均阻力系數為 1.15，與 Breuer［15］采用大渦模擬方法在相同雷諾數下得到的結果基本一致。斜置圓柱在均勻流作用下的平均阻力系數為0.98，與直立圓柱相比有所減少。在剪切流作用下，斜置圓柱的平均阻力系數隨著剪切系數的增大而增大，并逐漸接近均勻流作用下直立圓柱的平均阻力系數。平均阻力系數的這種變化趨勢與平均風壓系數的變化規律相同。

在圓柱傾角和剪切流影響下，升力系數時程較阻力系數時程的變化更為劇烈。在均勻流作用下，斜置圓柱的升力時程曲線與直立圓柱相比，升力的波動幅度大大降小，并且升力波動的規律性也降低了。這可能是因為斜置圓柱的卡門渦脫的強度和規律性受到軸向流的影響導致的。對于斜置圓柱，隨著剪切流剪切系數的增大，升力時程曲線的波動幅度逐漸增大，規律性也逐步增強。這說明剪切流可增強斜置圓柱尾流區的卡門渦脫強度。

圖8為上述四種情況下升力系數的頻率譜(PSD)。由圖可得，在均勻流作用下，斜圓柱的卡門渦脫強度比直立圓柱明顯降低。這與Matsumoto等［5］所得結論基本一致，在斜置圓柱的尾流區會形成強烈的軸向流，而軸向流會干擾尾流區的卡門渦脫，從而導致卡門渦脫的下降。而在剪切流作用下，斜置圓柱體的卡門渦脫再次得到增強，并且卡門渦的強度隨剪切系數的增大而增強。

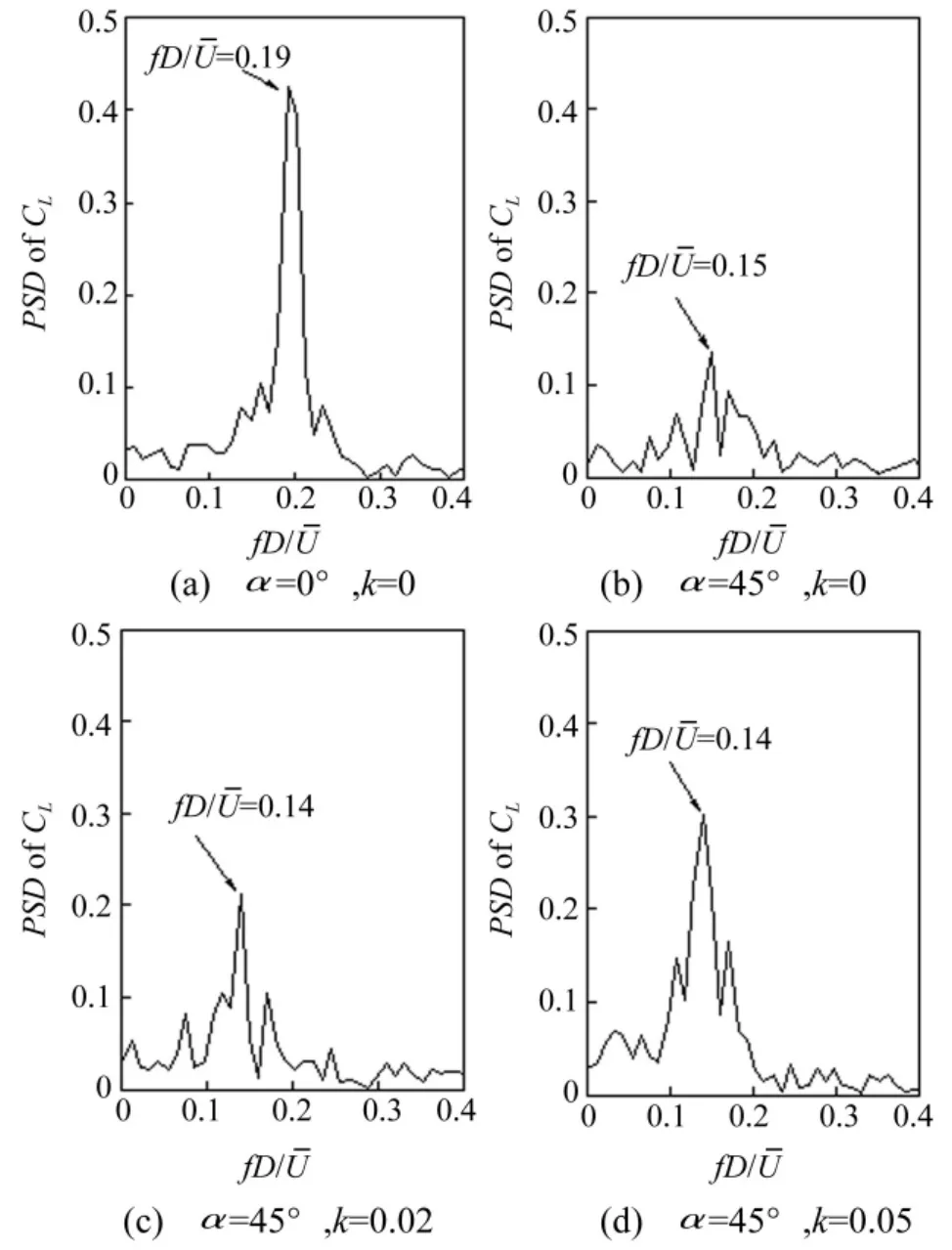
圖8 升力系數功率譜Fig.8 Power spectra density of lift coefficients

對于St，均勻流作用下的直立圓柱為0.19，而斜置圓柱為0.15。對于斜置圓柱，剪切流的剪切系數基本不影響St數的大小。

3.5 氣動力展向相關性

圖9是圓柱展向不同截面的氣動力系數之間的相關系數。各截面之間的無量綱間距的計算方法見表2，截面位置見圖1。

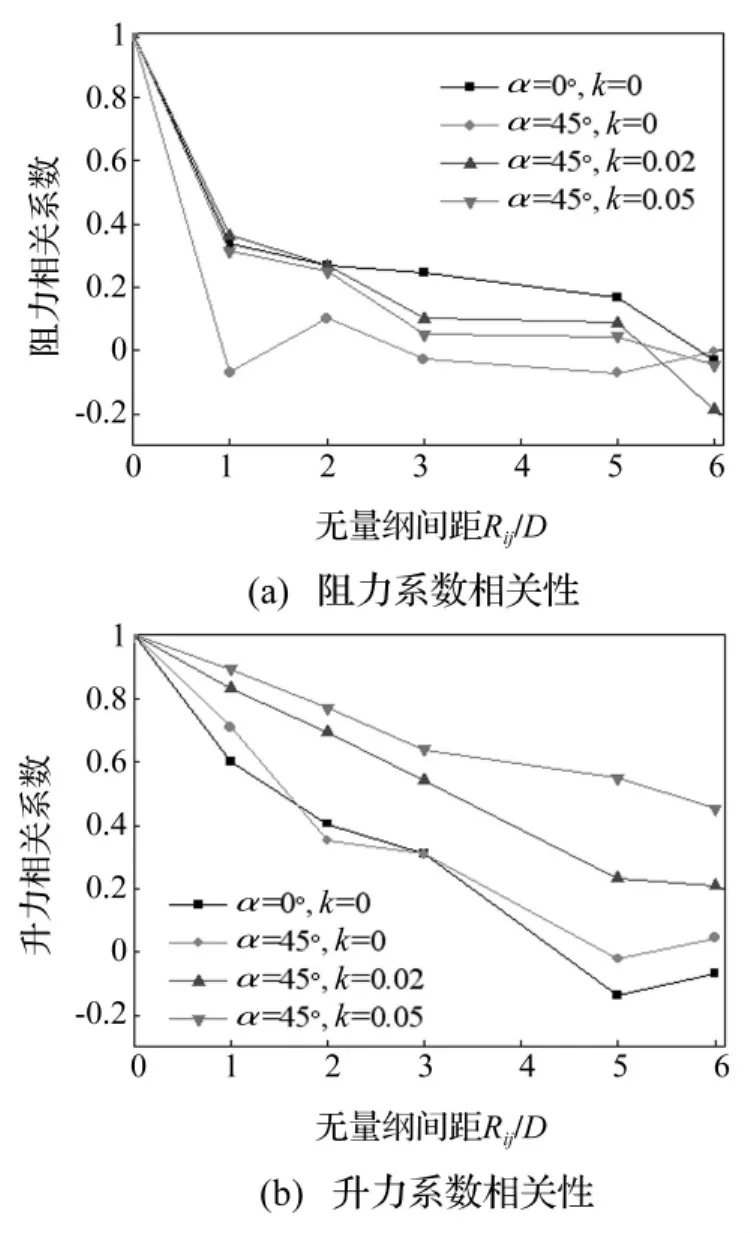
圖9 氣動力系數的相關性Fig.9 Correlation coefficients of lift coefficients

從總體上看，阻力系數的展向相關性較升力系數差，傾角和剪切流對阻力系數的影響較升力系數小。從圖9(a)可見，在均勻流作用下，直立圓柱的阻力系數相關性比斜置圓柱略好;而在剪切流作用下，斜置圓柱阻力系數的相關性略有增強。從圖9(b)可見，在均勻流作用下，直立圓柱與斜置圓柱的升力相關性比較接近，這說明升力系數對圓柱的傾角不是敏感。但在剪切流作用下，斜置圓柱的升力相關性隨著剪切系數的增大而增強，與直立圓柱的升力相關性相比有很大的提高。

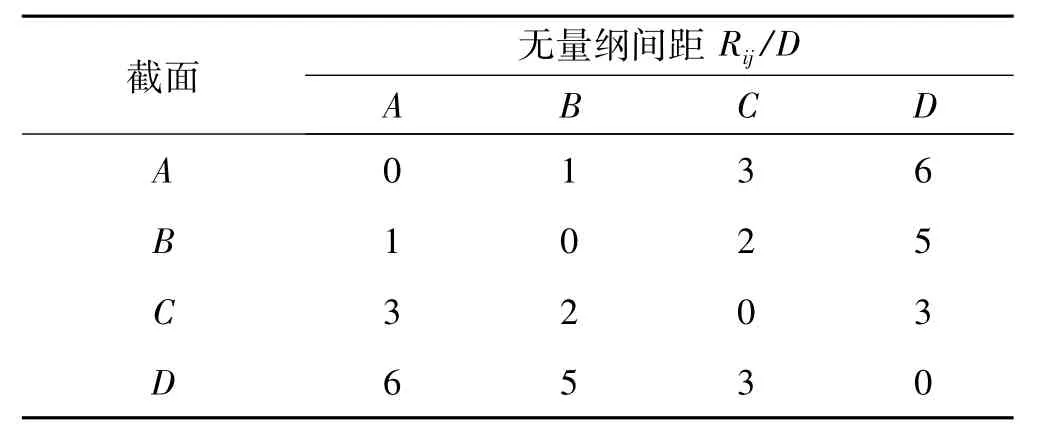
表2 各截面無量綱間距Tab.2 Dimensionless distance between different sections

3.6 機理分析

圖10為斜置圓柱在均勻流和剪切流作用下的流線圖。由圖10(a)可見，在均勻流作用時，流線在接近圓柱迎風側時，會沿著圓柱軸線方向移動;然后再向圓柱橫截面方向彎曲并繞經圓柱;流線繞過圓柱并沿圓柱軸線方向移動一段距離后分為兩部分，一部分繼續沿著軸向流動，另一部分則沿著與來流方向相近的方向向圓柱后移動。這說明:在均勻流作用下，傾角為45°的斜置圓柱尾流區會產生強烈的軸向流。這一現象與Zhao等［8］在雷諾數為1 000時采用DNS計算得到的結果相似。斜置圓柱尾流區的軸向流會干擾卡門渦脫，降低卡門渦脫強度(見圖8(b))，從而導致升力時程波動幅度的大幅減小(見圖7(b))。這些結論與Matsumoto等［5］的研究結論相一致。由圖10(b)和圖10(c)可見，在剪切流作用下，隨著剪切流強度的增大，斜置圓柱尾流區的軸向流強度有逐漸減弱的趨勢，并且當剪切流系數達到0.05時，圓柱尾流區的軸向流現象基本消失。

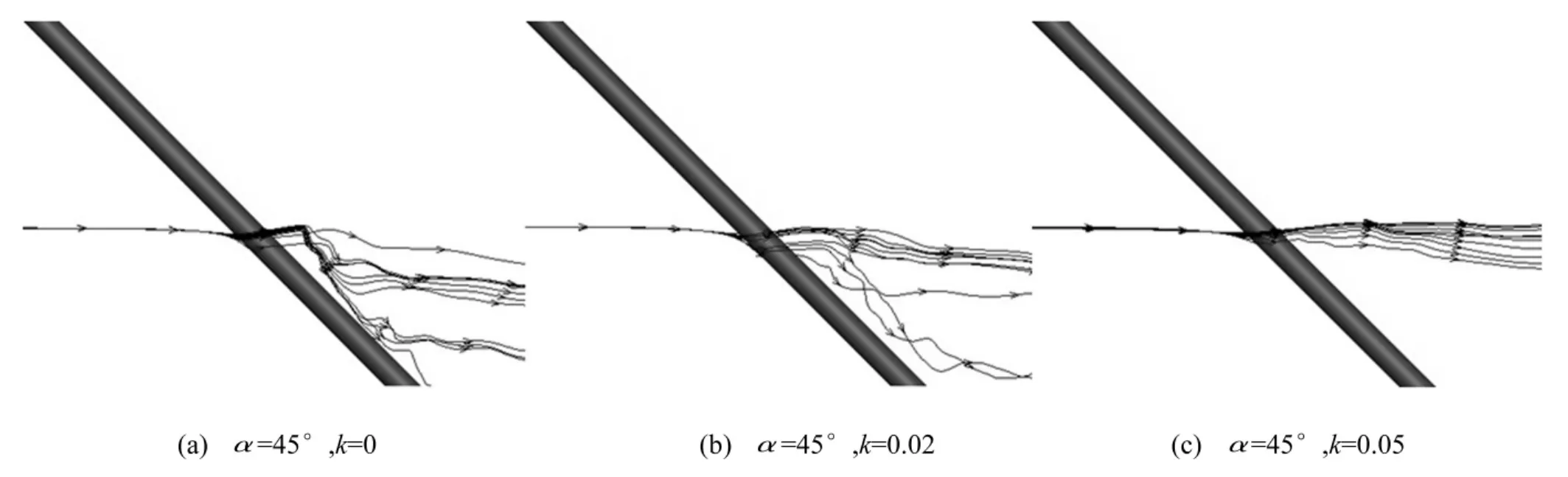
圖10 斜置圓柱流線圖Fig.10 The oblique cylindrical streamline

為了進一步分析剪切流對斜置圓柱的作用機理。圖11列出了直立圓柱在均勻流和剪切流作用下的流線圖。由圖11(a)可見，在均勻流作用下，直立圓柱尾流區的流線幾乎與來流方向相同，流線繞過圓柱后沿著與來流方向相近的方向向圓柱后移動。而在剪切流作用下，見圖11(b)，流線繞過圓柱后分為兩部分，一部分沿著與來流方向相近的方向向圓柱后移動;另一部分則沿著圓柱展向向上流動，流動一定距離后再沿著與來流相近的方向向圓柱后側移動。這說明在剪切流作用下，在圓柱后側也會形成軸向流，但剪切流引起的軸向流的流動方向與圖10(a)中斜置圓柱的軸向流方向相反。

從以上的分析可以推斷:對于展向剪切流作用下的斜置圓柱，由于剪切流引起的軸向流與斜置圓柱尾流區的剪切流方向相反，隨著剪切流強度的增大，剪切流形成的軸向流可減弱或甚至抑制斜置圓柱的軸向流。這也解釋了斜置圓柱的卡門渦脫強度會隨著剪切流剪切系數的增大而增強的原因(見圖8):在均勻流作用下，斜置圓柱尾流區會產生沿圓柱軸向流動的軸向流，軸向流會干擾并減弱卡門渦脫的強度;但展向剪切流則會破壞軸向流在尾流區的形成，消除了導致卡門渦脫減弱的因素，使得斜置圓柱的卡門渦脫的強度得到增強。

圖11 直立圓柱流線圖Fig.11 The vertical cylindrical streamline

4 結論

本文采用大渦模擬方法，對展向剪切流作用下斜置圓柱的氣動性能和流場特征進行了研究，得到以下結論:

(1)在均勻流作用下，斜置圓柱尾流區會產生強烈的軸向流，而軸向流的出現會減弱卡門渦脫強度，并導致圓柱表面的脈動風壓系數降低、圓柱平均阻力系數減小、升力時程的波動幅度減弱;

(2)隨著展向剪切流強度的增大，斜置圓柱的平均阻力系數逐漸增大，升力時程的波動幅度也會增強，但剪切流對Strouhal數的影響很小;

(3)在展向剪切流作用下，斜置圓柱升力的展向相關性隨著剪切系數的增大而增強，剪切流對阻力的展向相關性則影響較小;

(4)對于斜置圓柱，展向剪切流會減弱或抑制軸向流在圓柱尾流區的形成，并且當剪切流的剪切系數足夠大時，可完全抑制軸向流的出現。從而減弱或消除了抑制卡門渦脫的因素，使斜置圓柱的卡門渦脫強度得到恢復。

［1］Zdravkovich M M.Flow around circular cylinders［M］.Oxford:Oxford University Press，1997.

［2］Ramberg SE.The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders［J］.Journal of Fluid Mechanics，1983，128:81 －107.

［3］杜曉慶，顧明.斜置拉索表面脈動風力特性研究［J］.振動與沖擊，2012，31(4):139－144.DU Xiao-qing，GU Ming.Characteristics of fluctuating forces on inclined stay cable［J］.Journal of Vibration and Shock，2012，31(4):139 －144.

［4］杜曉慶，顧明.臨界雷諾數下斜拉橋拉索的平均風壓和風力特性［J］.空氣動力學學報，2010，28(6):639－644.DU Xiao-qing，GU Ming.Wind pressure distribution and aerodynamic characteristic of stay cable in the critical Reynolds number regime［J］.Acta Aerodynamica Sinica，2010，28(6):639 －644.

［5］ Matsumoto M，Yagi T，Hatsuda H，et al.Dry galloping characteristics and its mechanism of inclined/yawed cables［J］. Journal of Wind Engineering and Industrial Aerodynamics，2010，98(6－7):317－327.

［6］Marshall J S.Wake dynamics of a yawed cylinder［J］.ASME Journal of Fluids Engineering，2003，125(1):97－103.

［7］Yeo D H，Jones N P.Investigation on 3－D characteristics of flow around a yawed and inclined circular cylinder［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(10－11):1947－1960.

［8］Zhao M，Cheng L，Zhou T M.Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length ［J］.Journal of Fluids and Structures，2009，25(5):831－847.

［9］Griffin O M.Vortex shedding from bluff bodies in a shear flow:A review ［J］.ASME Journal of Fluids Engineering，1985，107(3):298－306.

［10］Woo H G C，Cermak JE，Peterka JA.Secondary flows and vortex formation around a circular cylinder in constant-shear flow ［J］.Journal of Fluid Mechanics，1989，204:523－542.

［11］ Kappler M，Rodi W，Szepessy S，et al.Experiments on the flow past long circular cylinders in a shear flow ［J］.Experiment in Fluids，2005，38(3):269－284.

［12］ Xu Y，Dalton C.Computation of force on a cylinder in a shear flow［J］.Journal of Fluids and Structures，2001，15(7):941－954.

［13］Mukhopadhyay A，Venugopal P，Vanka SP.Oblique vortex shedding from a circular cylinder in linear shear flow ［J］.Computer＆ Fluids，2002，31(1):1－24.

［14］ Parnaudeau P， Heitz D， Lamballais E，et al. Direct numerical simulations of vortex shedding behind cylinders with spanwise linear nonuniformity ［J］. Journal of Turbulence，2007，8(13):1－13.

［15］Breuer M.Numerical and modeling influences on large eddy simulations for the flow past a circular cylinder ［J］.International Journal of Heat and Fluid Flow，1998，19(5):512－521.

［16］ Cardell G S.Flow past a circular cylinder with a permeable splitter plate［D］，Ph.D.Thesis，Graduate Aeronautical Laboratory，California Institute of Technology，1993.