參數擾動廣義混沌同步化線譜控制技術研究
楊慶超,何其偉,孫方旭
(海軍工程大學 科研部,武漢 430033)
隨著隱身技術和反潛技術的發展,艦船輻射水聲線譜已成為被動聲納進行目標參數估計和類型識別的主要依據[1]。由于艦船機械設備大部分為旋轉類機械,工作工況相對穩定,則每艘艦船的輻射水聲線譜相對較為穩定,因此,線譜稱為艦船的“指紋”,對其隱身性能構成了嚴重危害。由于傳統的線性被動隔振系統具有頻率保持性,不能夠有效消除和改變線譜特征。針對這一難題,朱石堅等[2-3]提出了線譜混沌化控制技術,即利用非線性系統處于混沌運動狀態時,其功率譜呈連續譜且下降的特性對線譜特征進行控制,從而提高隱身性。
目前,線譜混沌化控制技術在原理驗證、隔振性能評估、混沌快速識別、試驗研究等方面均取得了成效[4-6]。為使非線性隔振系統由周期運動狀態轉變為混沌運動狀態,張振海等[7-11]提出了跟蹤混沌化控制技術、基于滑模控制的投影混沌同步控制技術、離散混沌化控制技術、反饋混沌化控制技術等和實時混沌化控制技術,但均需消耗較大的能量,使其難以應用到實際工程中。考慮到艦船隔振系統中應用了大量的氣囊隔振器,氣囊隔振器的氣壓對其剛度特性具有重要影響,且易于控制調節,消耗能量小,本文提出了基于參數擾動的廣義混沌同步線譜控制技術。
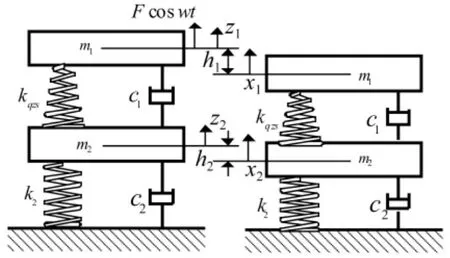
圖1 考慮柔性基礎的準零剛度隔振系統Fig.1 Vibration isolation system with flexible foundation
1 雙層隔振系統數學模型及動力學特性
根據牛頓第二定律,系統動力學方程為:

式中,F cos wt為系統外激勵力,k1為氣囊隔振器的剛度,c1為氣囊隔振器阻尼系數,k2為柔性基礎的剛度,c2為柔性基礎阻尼系數,Z1為彈簧處于自然狀態時被隔振物體的位移,Z2為彈簧處于自然狀態時中間質量塊的位移,m1為被隔振物體的質量,m2為中間質量塊的質量。
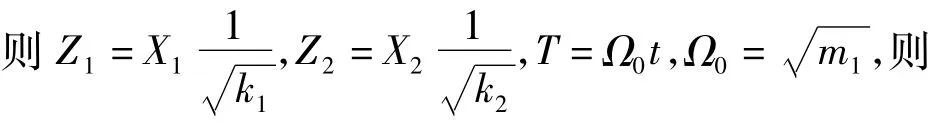
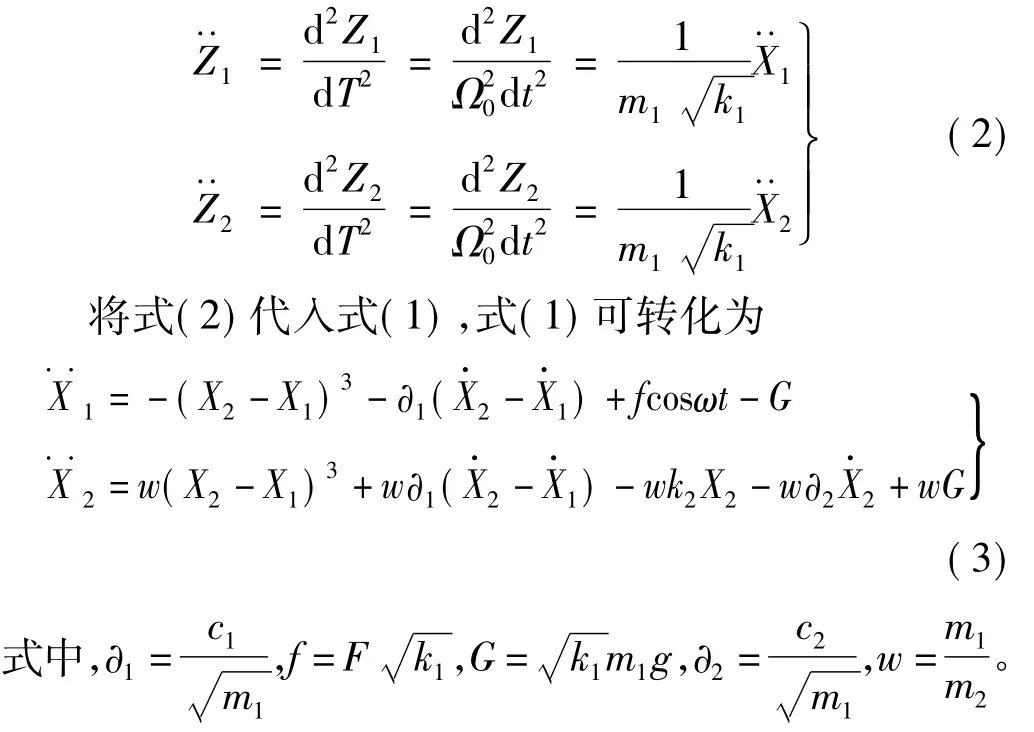
令參數1=0.1,2=0.1,w=0.2,G=2,f=25,ω=4,則雙層隔振系統無外界參數擾動時,雙層隔振系統的相圖和功率譜圖如圖2和3所示。由圖可知,系統處于單周期運動狀態,且激勵頻率處(ω=4)的線譜特征非常明顯,此時的線譜強度為0.203 4 dB。
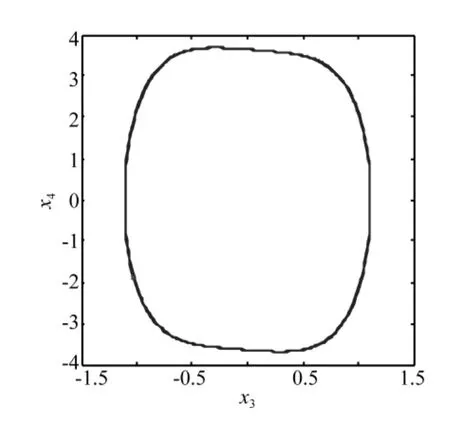
圖2 系統底板相圖Fig.2 The phase diagram of the system base
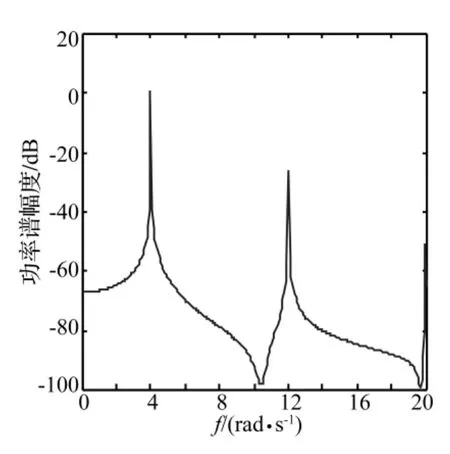
圖3 系統底板功率譜圖Fig.3 The power spectrum diagram of the system base

圖4 Duffing系統相圖Fig.4 The phase diagram of the Duffing system
2 數值仿真
以外界混沌系統的某一輸出信號為驅動信號,對氣囊隔振器的氣壓進行控制,即控制隔振系統的剛度,實現隔振系統的廣義混沌同步化,從而達到削弱特征線譜強度和改變頻譜結構的效果。
2.1 驅動系統為Duffing系統時線譜控制效果
Duffing系統的方程為
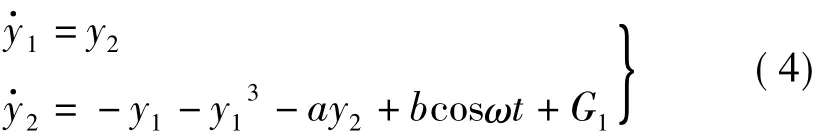
當 Duffing系統參數 a=0.08,b=9.2,G1=2,ω =4,初始條件為(0,0)時[6],系統的相圖和功率譜圖如圖4和圖5所示。由圖4可知,此時Duffing系統的軌跡充滿了整個相空間,圖中的紅色點表示周期軌道的個數,分布在相空間的多個紅色點表示此時系統的周期軌道是互相纏繞在一起的。由圖5可知,此時Duffing系統的功率譜呈現連續譜特性,綜上所述,可判斷此時Duffing驅動系統處于混沌運動狀態。
以Duffing系統為外界驅動系統,以Duffing系統的輸出信號y2為驅動信號,對雙層隔振系統的剛度進行擾動,擾動強度為k,則該耦合系統的方程如式(5)所列。為使結果具有可比性,耦合系統的參數取值與上述保持一致。耦合系統功率譜最強線譜隨擾動強度的變化趨勢如圖6所示。由圖6可知,當k在0附近取值時,系統最強線譜強度會降低,即在較小的擾動情況下系統將跟隨Duffing驅動系統運動,并使線譜強度得到抑制。當k=0.068時,底板的相圖和功率譜圖如圖7和圖8所示,由圖可知,系統運動軌跡充滿了整個相圖空間且功率譜呈現連續譜特性,即系統由單周期運動狀態轉變為了混沌運動狀態。一方面,特征線譜強度(ω=4)得到了有效的抑制,此時的特征線譜強度為-61.756 9 dB,比無 Duffing系統驅動時降低了61.960 3 dB。另一方面,系統的頻譜結構發生了較大的改變,提高了系統的偽裝性能。當k=0.086時,底板的相圖和功率譜圖如圖9和圖10所示,由圖可知,在該種情況下,同樣可取得良好的效果。
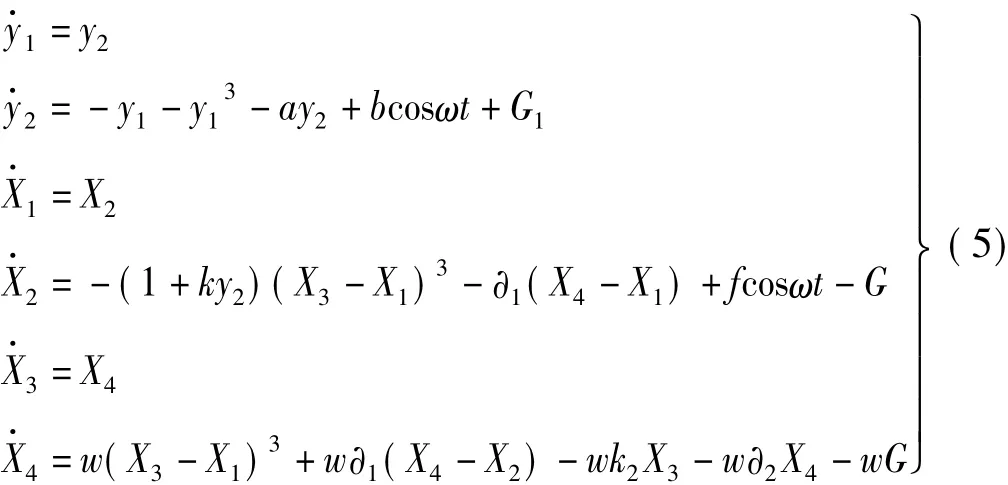
2.2 驅動系統為Lorenz系統時線譜控制效果
Lorenz系統的方程為
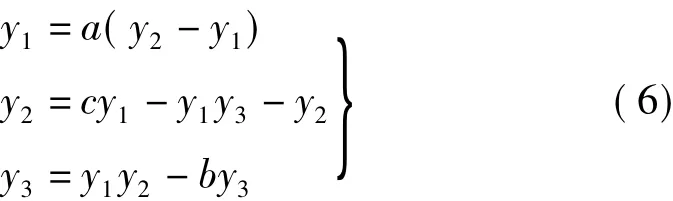
當 Lorenz系統參數 a=10,b=8/3
,c=28,初始條件為(1,1)時,系統的相圖和功率譜圖如圖11和圖12所示。由圖11可知,此時Lorenz系統的運動軌跡纏繞在一起并充滿了整個相空間。由圖12可知,此時Lorenz系統的功率譜呈現比較平坦的連續譜特性,綜上所述,可判斷此時Lorenz驅動系統處于混沌運動狀態。
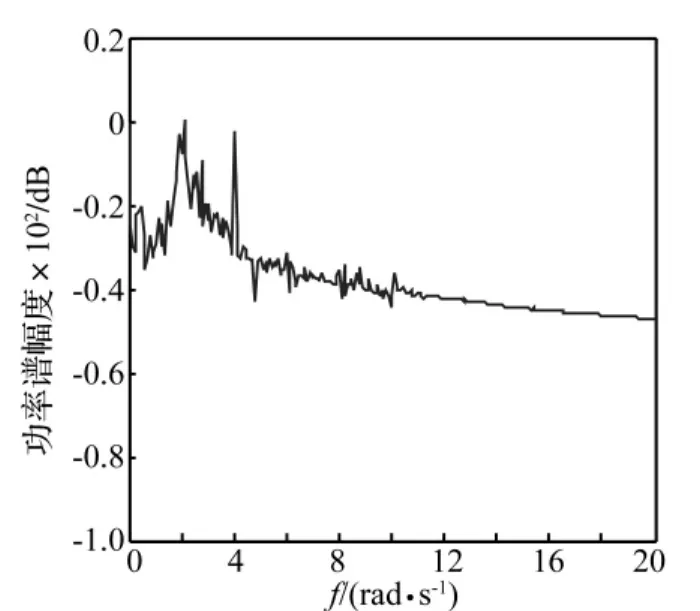
圖5 Duffing 系統功率譜圖Fig. 5 The power spectrum diagram of theDuffing system
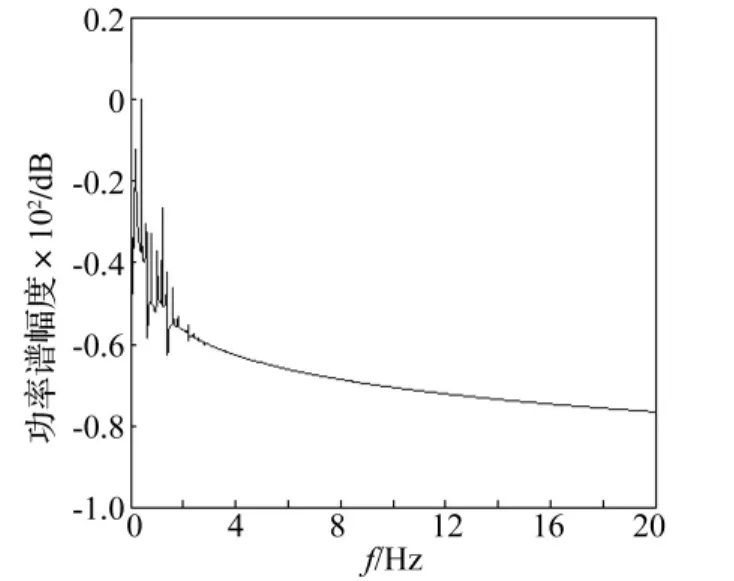
圖8 當k=0.068時耦合系統功率譜圖Fig.8 The power spectrum diagram of coupled system of k=0.068
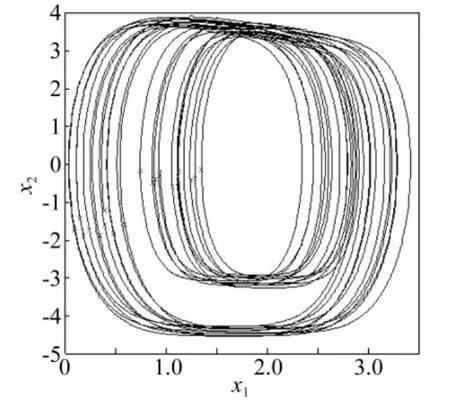
圖9 當k=0.086時耦合系統相圖Fig.9 The phase diagram of coupled system of k=0.086
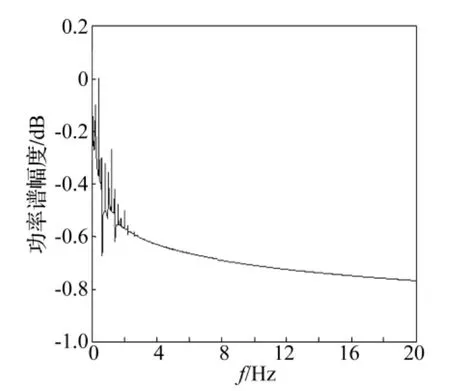
圖10 當k=0.086時耦合系統功率譜圖Fig.10 The power spectrum diagram of coupled system of k=0.086
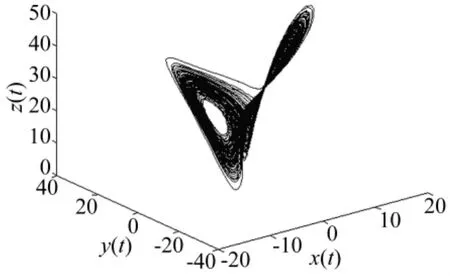
圖11 Lorenz系統的相圖Fig.11 The phase diagram of theLorenz system
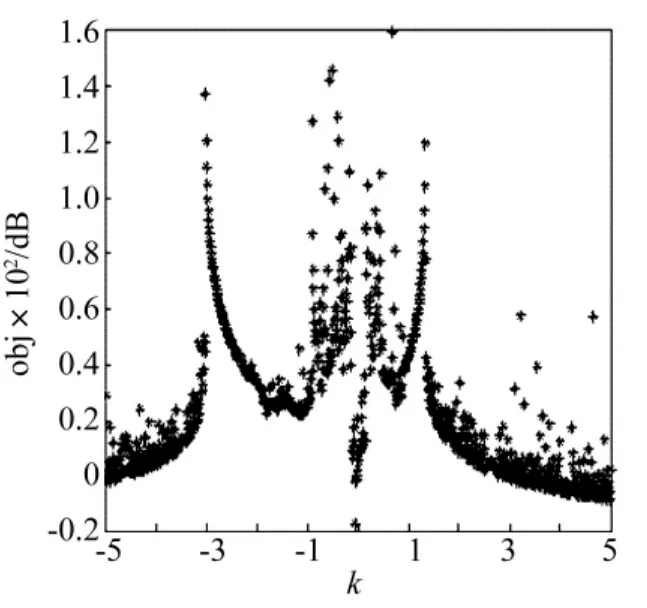
圖6 耦合系統最強線譜與k的變化趨勢Fig.6 The largest line spectrum of coupled system for various values of k
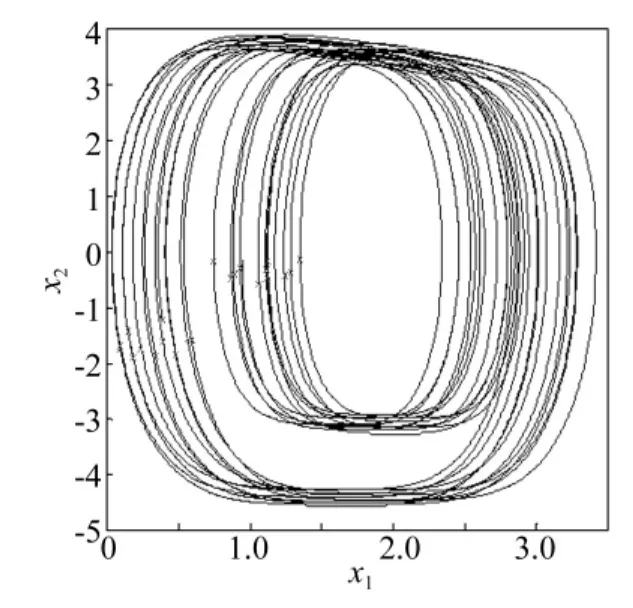
圖7 當k=0.068時耦合系統相圖Fig.7 The phase diagram of coupled system of k=0.068
以Lorenz系統的輸出信號y1作為驅動信號,對雙層準零剛度系統的剛度進行擾動,此時耦合系統的方程如式(7)所列。系統參數取值與上面保持一致,耦合系統的最強線譜隨擾動強度k的變化趨勢如圖13所示。由圖13可知,當擾動強度k的取值在0附近時,系統最強線譜的幅度最小,即利用較小的外界能量能夠使系統的線譜強度得到有效的抑制。當k=0.001時的相圖和底板位移功率譜圖如圖14和圖15所示,由圖可知,系統已轉化為混沌運動狀態,與無外界驅動時的功率譜圖3相比,系統的特征線譜強度的得到了有效抑制,由原來的0.203 4 dB 降到了 -15.620 3 dB,且功率譜的整體強度均有所下降。當k=0.003時的相圖和底板位移功率譜圖如圖16和圖17所示,通過比較圖17和圖3可得,此時亦能得到良好的線譜控制效果,特征線譜強度降低了15.866 1 dB。
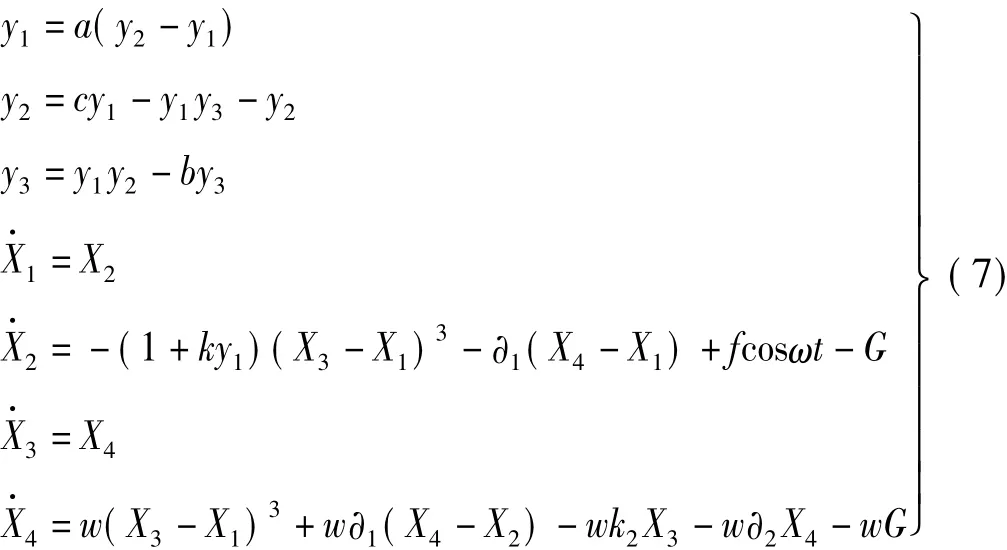
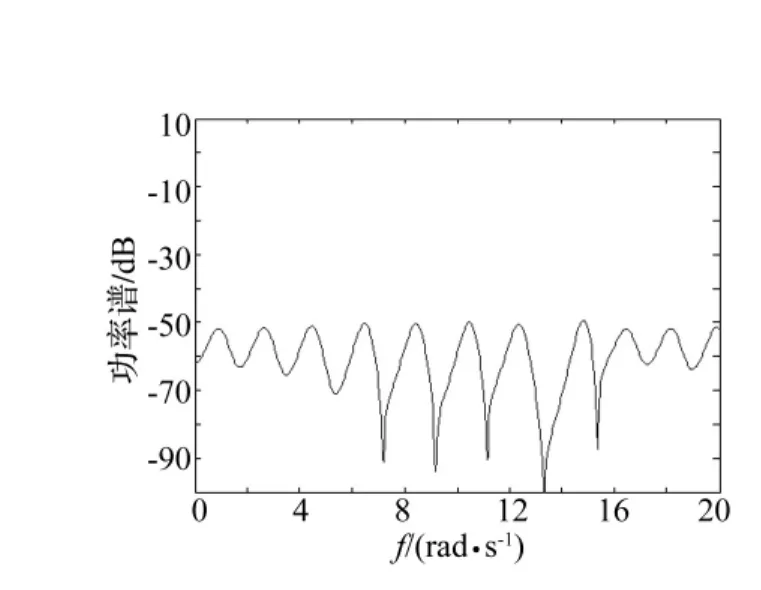
圖12 Lorenz系統功率譜圖Fig.12 The power spectrum diagram of the Lorenz system

圖13 耦合系統最強線譜與k的變化趨勢Fig.13 The largest line spectrum of coupled system for various values of k
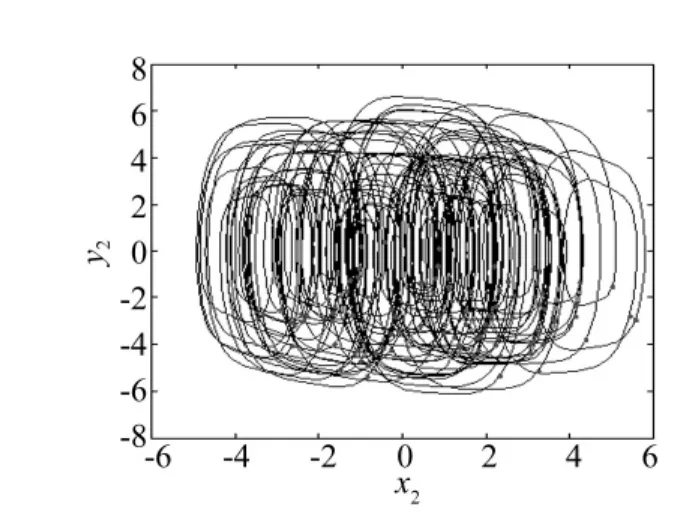
圖14 當k=0.001時耦合系統相圖Fig.14 The phase diagram of coupled system of k=0.001
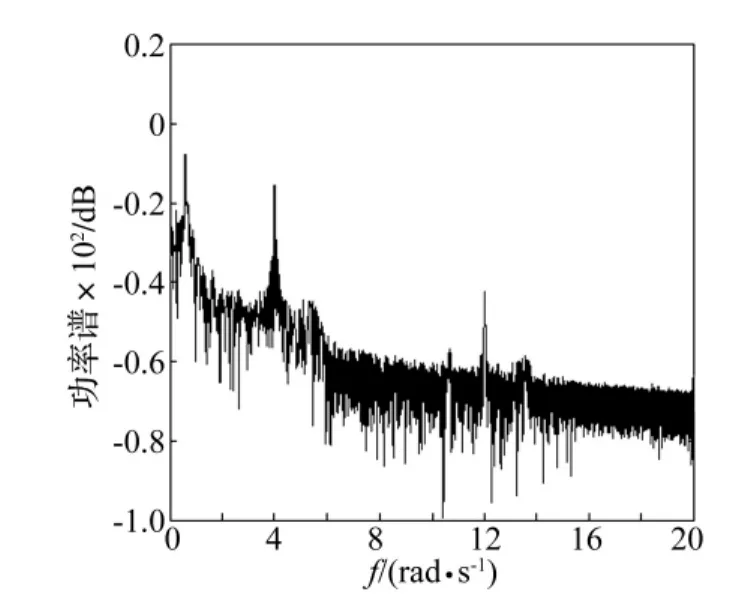
圖15 當k=0.001時耦合系統功率譜圖Fig.15 The power spectrum diagram of coupled system of k=0.001

圖16 當k=0.003時耦合系統相圖Fig.16 The phase diagram of coupled system of k=0.003
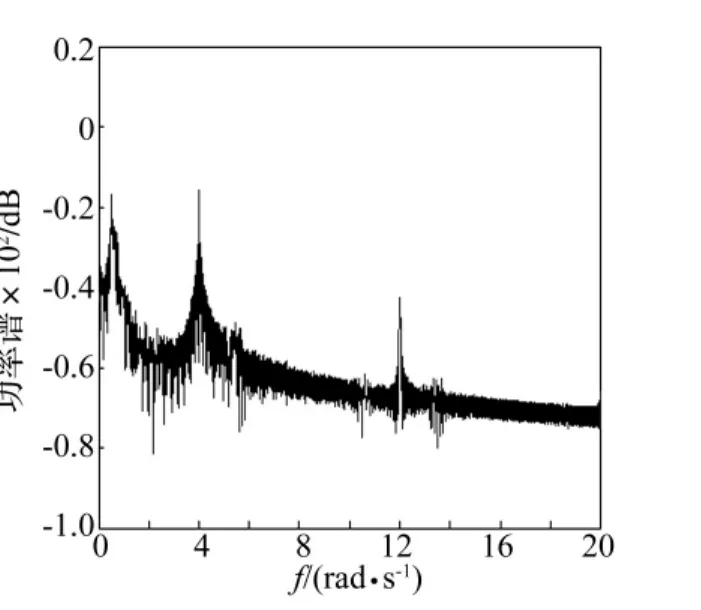
圖17 當k=0.003時耦合系統功率譜圖Fig.17 The power spectrum diagram of coupled system of k=0.003
3 結論
針對線譜混沌化技術工程化應用的瓶頸問題,即如何在小能量消耗條件下使隔振系統由周期運動狀態轉變為混沌運動狀態。根據船用隔振系統的特點,提出了參數擾動廣義混沌同步線譜控制技術,并進行了數值仿真,結果表明:
(1)參數擾動廣義混沌同步化控制技術能夠利用較小的控制能量使系統由周期狀態轉變為混沌運動狀態,為有效解決線譜混沌化方法工程化應用的瓶頸問題提供了思路。
(2)利用功率譜特性較為平坦的系統作為驅動系統時,受控系統達到混沌運動狀態后,不僅線譜強度得到有效控制,整體譜強度均有所降低,提高了艦船的隱身性能。
[1]朱英富,張國良.艦船隱身技術[M].哈爾濱:哈爾濱工程大學出版社,2003.
[2]朱石堅,姜榮俊,何琳.線譜激勵的混沌隔振研究[J].海軍工程大學學報,2003,15(1):19 -22.ZHU Shi-jian,JIANG Rong-jun,HE Lin.Study on chaotic vibration isolation line spectrum excitation[J].Journal of Naval University of Engineering,2003,15(1):19 -22.
[3] Jiang R J,Zhu S J.Vibration isolation and chaotic vibration[C]//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2005,Chicago,ASME Press,2005:2375 -2377.
[4] Lou J J,Zhu SJ,He L,et al.Application of chaos method to line spectra reduction[J].Journal of Sound and Vibration,2005,286(3):645 -652.
[5]朱石堅,劉樹勇.混沌振動識別的研究[J].武漢理工大學學報(交通科學與工程版),2003,27(6):766-769.ZHU Shi-jian,LIU Shu-yong.Study on chaotic vibration identification[J].Journal of Wuhan University of Technology(Transportation Science & Engineering),2003,27(6):766 -769.
[6] YU Xiang,ZHU Shi-jian,LIU Shu-yong.A new method for line spectra reduction similar to generalized synchronization of chaos[J].Journal of Sound and Vibration,2007,306:835-848.
[7]張振海,朱石堅,樓京俊.基于跟蹤混沌化方法的線譜控制技術研究[J].振動與沖擊,2011,30(7):40-44.ZHANG Zhen-hai, ZHU Shi-jian, LOU Jing-jun. Line spectra reduction of a vibration isolation system based on tracking chaotification method[J].Journal of Vibration and Shock,2011,30(7):40 -44.
[8]曾強洪,朱石堅,樓京俊,等.基于滑模控制投影混沌同步在隔振系統中的應用研究[J].振動與沖擊,2010,29(12):114-117.ZENG Qiang-hong,Zhu Shi-jian,LOU Jing-jun,et al.Study on the application of projective synchronization to vibration isolation system based on sliding mode control[J].Journal of Vibration and Shock,2010,29(12):114 -117.
[9]張振海,朱石堅,樓京俊.基于離散混沌化方法的線譜控制技術研究[J].振動與沖擊,2010,29(10):50-52.ZHANG Zhen-hai,ZHU Shi-jian,LOU Jing-jun.A new method of discrete chaotification for line spectra reduction of a vibration isolation system [J].Journal of Vibration and Shock,2010,29(10):50 -52.
[10]張振海,朱石堅,何其偉.基于反饋混沌化方法的多線譜控制技術研究[J].振動工程學報,2012,25(1):30-37.ZHANG Zhen-hai,ZHU Shi-jian,HE Qi-wei.Multi-line spectra reduction of vibration isolation system based on chaotification method[J].Journal of Vibration Engineering,2012,25(1):30-37.
[11]周加喜,徐道臨,張月英,等.一種針對未知參數系統的實時混沌化方法[J].振動與沖擊,2013,32(4):71-74.ZHOU Jia-xi,XU Dao-lin,ZHANG Yue-ying,et al.A realtime chaotification method for dynamic systems with unknown parameters[J].Journal of Vibration and Shock,2013,32(4):71-74.

