旋轉機翼無人機巡航狀態飛行力學模型辨識
王斑, 詹浩, 黃晶
(西北工業大學 航空學院, 陜西 西安 710072)
0 引言
鴨式旋翼機翼無人機兼顧直升機和固定翼飛機的飛行特點,以直升機模式進行起飛、降落以及小速度前飛,以三翼面固定翼模式進行高速巡航[1]。為了兼顧直升機模式和固定翼模式的不同特性,中間旋翼機翼采用橢圓翼型。在飛行過程中,旋翼機翼與機身及后置平尾之間的干擾復雜,很難準確獲得飛機的飛行力學模型。
通過傳統的方法建立鴨式旋翼機翼無人機的飛行力學模型需要進行大量的測量和風洞試驗,這將花費大量的人力、物力,因而是不經濟的。為了滿足無人機飛行控制系統的設計要求,系統辨識以其簡潔、高效、低成本的特點成為傳統建模思想的替代方法。并且,由于對無人機進行系統辨識易于開展、成本低廉,所以通過對無人機系統辨識的研究,也可以為其他飛行器飛行力學模型的系統辨識提供經驗。
本文主要研究巡航狀態下鴨式旋翼機翼無人機飛行力學模型的系統辨識方法。首先通過機理建模建立試驗無人機的縱橫向通道的參數化模型;然后進行掃頻飛行試驗,利用頻域辨識技術從飛行數據中提取某個通道的線性模型,并從中獲得關鍵參數的值;最后進行時域驗證,通過比較模型預測數據和飛行試驗數據表明,該模型很好地反映了無人機在巡航狀態下的動態特性。該方法和純機理建模相比,具有易工程化、工作點附近模型準確性高等優點,并且可以基于此模型進行飛行控制系統設計。
1 辨識機理模型建立
系統辨識的一個重要內容就是利用先驗知識確定辨識對象的模型結構,辨識模型的結構決定了辨識結果與真實物理系統動力學特性的相符程度,這在很大程度上影響模型擬合的精度和模型的可靠性。
模型選擇需要結合該型無人機的飛行特點,選擇符合實際飛行動態的模型結構會大大降低辨識的難度,提高模型的精度和可靠性。在飛機設計及控制系統設計初期,通過傳遞函數可以了解飛機的動態特性及飛機的飛行品質。通過簡化可以得到飛機縱、橫向傳遞函數模型[2-3]:
(1)
(2)
式中,Tθ2為分子時間常數;τθ,τφ為時間延遲;Ts和Tr分別為螺旋模態和滾轉模態的時間常數。
2 頻域辨識算法
根據鴨式旋翼機翼無人機的動力學特性,設計飛行掃頻試驗,通過對試驗數據進行一致性分析和濾波處理得到頻域辨識所需的數據[4]。為了減少有限傅立葉變換引起的頻譜泄露,使用復合窗函數法對原始試驗數據進行處理,之后利用FFT算法將加窗后的數據轉換到頻域,得到優化的非參數頻率響應。通過參數尋優的方法,擬合特定頻段內待辨識模型與實測數據的頻率響應,得到機理模型中待辨識參數的值。
2.1 基于功率譜密度函數的頻率響應估計
典型的飛行器動態響應測量值,如角速率陀螺、加速度計、氣動側滑角和迎角測量值會明顯受到來自機械、電子、大氣擾動等方面的干擾,這些干擾是輸出測量噪聲的主要來源。因此認為噪聲作用于輸出端,并且輸入測量不受噪聲的干擾,系統的頻率響應可用如下功率譜分析方法[5]得到:
H(f)=Gxy(f)/Gxx(f)
(3)
式中,H(f)為輸入x與輸出y之間的頻率響應;Gxy(f)為輸入與輸出之間的互譜;Gxx(f)為輸入數據的自譜。
由于不同通道之間存在耦合,在從輸入到輸出的系統中存在不能用頻率響應H(f)描述的非線性特性、過程噪聲和測量噪聲的影響。因此引入相干函數,它是判斷在頻率點f上,輸出譜Gyy中由輸入譜Gxx線性地引起的部分在整個輸出譜中所占的比例,其相干函數表達式為:
(4)
2.2 復合分窗分析
重復的機動首先連接成為串接記錄,這些記錄分段成為更短的時間重疊記錄序列,稱為窗口。數據分窗可以降低譜估計中的隨機誤差。
典型的窗口尺寸選擇將在最小有效頻率和最大感興趣的頻率ωmax之間提供至少10個數據帶寬。最大窗口尺寸通常應限制于單個記錄長度的50%。由此可得:
20×2π/ωmax≤Twin≤0.5Trec
(5)
式中,Twin為窗口長度;Trec為單個記錄長度。
最終窗口長度的選擇是權衡的結果,要兼顧低頻增加信息量的需求(需要大窗口)和抑制隨機誤差的需求(需要小窗口)。本文采用加權的復合窗口法來提高頻率響應精度。頻率響應估計中的隨機誤差定義為:
(6)
使用的加權函數[6]為:
Wi=[(εr)i/(εr)min]-4
(7)
式中,(εr)i為該窗口下某頻率響應對式(6)的隨機誤差。最終譜函數的目標函數為:
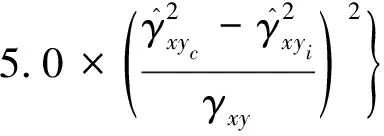
(8)
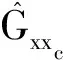
據此將飛行試驗掃頻得到的數據進行分窗分析,掃頻數據為174 s,分別進行5 s,10 s,20 s,25 s,34 s分窗。
2.3 參數化模型辨識
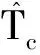
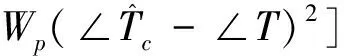
(9)
式中,|·|為每個頻率ω處的幅值;∠為每個頻率ω處的相位;nω為頻率采樣點的數量;ω1,ωnω分別為擬合的起始頻率值和結束頻率值。
代價函數越小說明辨識得到的模型越精確。當代價函數J≤50,則基本可以認為擬合結果相對飛行數據的差異很小。
3 飛行試驗設計和辨識結果分析
鴨式旋翼機翼無人機機身上裝有一套數據采集系統,其中包括一個三軸陀螺、一個三軸加速度計、一個GPS和一個飛控計算機,數據采樣頻率為50 Hz。外形如圖1所示。

圖1 鴨式旋翼機翼無人機Fig.1 The unmanned canard rotor wing aircraft
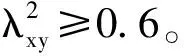
以縱向通道為例,其掃頻頻率響應和擬合頻率響應以及相干函數值如圖3所示。在低頻及高頻區模型與實際測量輸出相干性很低。
根據縱、橫向通道參數化模型式(1)和式(2),得到鴨式旋翼機翼無人機縱、橫向通道傳遞函數為:

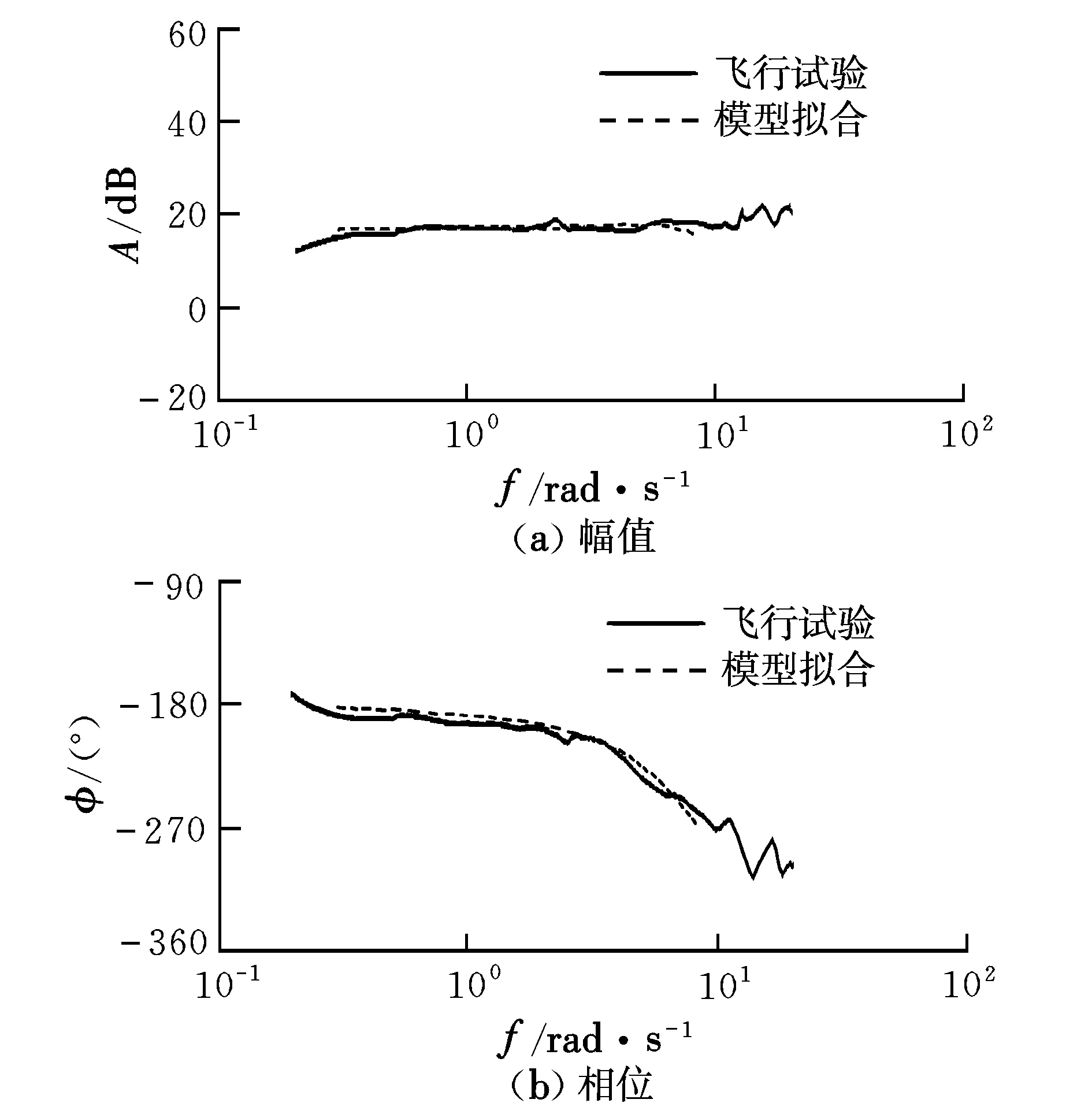
圖3 縱向通道頻率響應Fig.3 Frequency response of longitudinal channel
4 時域驗證
時域驗證是評估所辨識模型預測精度和可靠性的重要方法。必須確認模型沒有相對該辨識依據的試驗數據以及試驗飛行條件被過調。為了能較好地驗證模型的可信度,輸入信號必須和辨識時所選用的輸入信號不相似[7]。驗證數據采用同一架飛機不同架次的飛行試驗數據,并且試驗數據相隔時間較短,這樣能保證傳感器狀態等情況相似。
俯仰通道采用類似階躍的激勵信號,如圖4所示。滾轉通道采用類似雙極方波的激勵信號,如圖5所示。兩個通道的時域驗證結果如圖6、圖7所示。可以看出,不論采用何種激勵信號,辨識模型預測的響應與飛行試驗數據基本吻合,響應趨勢基本一致。
圖4 俯仰通道激勵信號Fig.4 Excitation signal of longitudinal channel

圖5 滾轉通道激勵信號Fig.5 Excitation signal of lateral channel

圖6 俯仰角速率的模型預測和實測輸出比較Fig.6 Comparison between prediction and practise
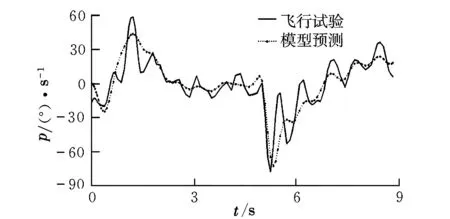
圖7 滾轉角速率的模型預測和實測輸出比較Fig.7 Comparison between prediction and practice
通過辨識獲得的模型可以計算出飛機各個模態的特征根如表1所示[8]。可以看出,鴨式旋翼機翼無人機具有較大的滾轉阻尼和俯仰阻尼,螺旋模態是緩慢發散的,這與實際試飛情況是一致的。
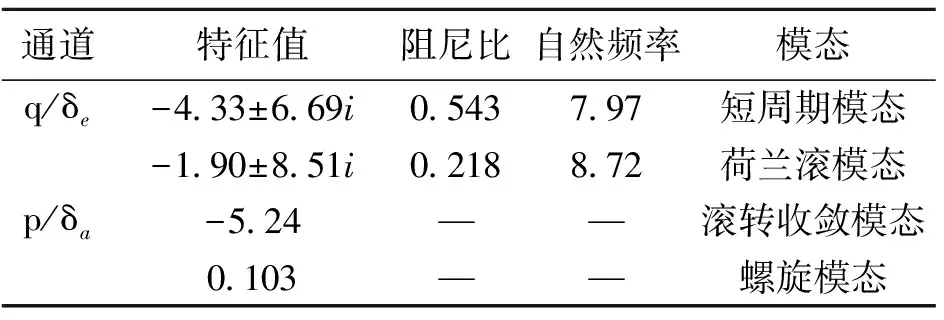
表1 縱、橫向通道特征值比較Table 1 Comparison of eigenvalue between longitudinal and lateral channel
綜上所述,得到的辨識模型能夠很好地預測鴨式旋翼機翼無人機在此飛行條件下的動力學響應特性。辨識得到的傳遞函數是正確和可信的,可以用于無人機品質分析以及增穩控制系統設計。
5 結束語
本文首先采用機理建模方法確定了鴨式旋翼機翼無人機巡航狀態下縱、橫向的傳遞函數模型,然后利用飛機縱、橫向掃頻飛行試驗數據及頻域辨識技術確定了待辨識模型的參數。通過時域驗證表明,模型預測的響應與飛行試驗數據基本吻合,證明了本文所建立的辨識方法是正確可行的;對后續鴨式旋翼機翼無人機其他飛行模態的辨識工作有一定的借鑒價值,對分析鴨式旋翼機翼無人機飛行品質以及增穩控制系統設計具有指導意義。
參考文獻:
[1] Mitchell C A,Vogel B J.The canard rotor wing(CRW) aircraft—a new way to fly[R].AIAA-2003-2517,2003.
[2] Tischler M B.Identification and verification of frequency-domain models for XV-15 tilt-rotor aircraft dynamics in cruising flight[J].Journal of Guidance,Control,and Dynamics,1986,9(4):446-452.
[3] Eggleston J M,Mathews C W.Application of several methods for determining transfer functions and frequency response of aircraft from flight data[R].Langley Field,Va:NACA TN 2997,1953.
[4] Tischler M B,Kaletka Jurgen. Modeling XV-15 tilt-rotor aircraft dynamics by frequency and time-domain identification techniques [R].Technical Report TM-89404,NASA,Moffett Field,CA,1986.
[5] Tischler M B,Remple R K.Aircraft and rotorcraft system identification:engineering methods with flight test examples[M].Blacksburg,Virginia:AIAA,2006:145-164.
[6] Strang G.Linear algebra and its applications[M].New York:Academic Press,1980:180-190.
[7] Theodore C R,Tischler M B,Colbourne J D.Rapid frequency-domain modeling methods for unmanned aerial vehicle flight control applications[J].Journal of Aircraft, 2004,41(4):735-743.
[8] 方振平,陳萬春,張曙光.航空飛行器飛行動力學[M].北京:北京航空航天大學出版社,2005:288-346.

