高超聲速滑翔飛行器多目標再入軌跡優化
任洋, 曹林平, 國海峰, 丁達理
(空軍工程大學 航空航天工程學院, 陜西 西安 710038)
0 引言
近年來,物理規劃方法[1]在解決多目標優化問題上顯現出較大的優勢,特別是它能夠根據設計者的偏好,得出合理的折中解。胡丹等[2]利用物理規劃解決了數據中繼衛星鏈路多目標配置決策問題,但對各項指標的產生辦法沒有做出解釋。龍瓊等[3]利用物理規劃對路徑誘導問題進行了定量描述,通過與A*算法的結合將路徑決策與駕駛者的偏好結合起來。雍恩米等[4]運用物理規劃解決了高超聲速滑翔飛行器再入軌跡優化問題,但其運動學模型只考慮了二維平面,沒有考慮地球自轉,相對簡單,且采用遺傳算法作為優化算法,若要達到較高尋優精度,所需運算時間相對較長。
本文以高超聲速滑翔飛行器三維再入段軌跡優化為研究對象,運用了hp自適應偽譜法,在物理規劃的框架下對多目標再入軌跡進行了尋優;針對hp自適應偽譜法的尋優特點,對物理規劃框架的偏好函數進行了改進,增大了其適用范圍;對不同偏好的再入段最優軌跡進行了仿真對比,為優化方案選擇提供了參考。
1 三自由度再入軌跡數學模型
飛行器再入軌跡數學模型包括飛行器三自由度動力學模型和氣動力模型。
1.1 飛行器動力學模型
考慮地球為旋轉圓球的三自由度再入運動模型為:
(1)
式中,r為地心距;θ為經度;φ為緯度;V為速度;γ為航跡角;ψ為航向角;ω,g,β,L,D分別為地球自轉角速度、引力加速度、側傾角、升力和阻力。
1.2 氣動力模型
在高超聲速飛行器再入過程中,要通過臨近空間穿過大氣層到達指定空域,而臨近空間大氣環境變化復雜,需對氣動模型進行較為精確的擬合。飛行器受到的升力L和阻力D的計算公式如下:
(2)
式中,S為氣動參考面積;ρ為大氣密度;升力系數CL(α,Ma)和阻力系數CD(α,Ma)的表達式為:
(3)
式(3)中的系數l(j),d(j)通過對X-33飛行數據進行擬合得到[5],如表1所示。
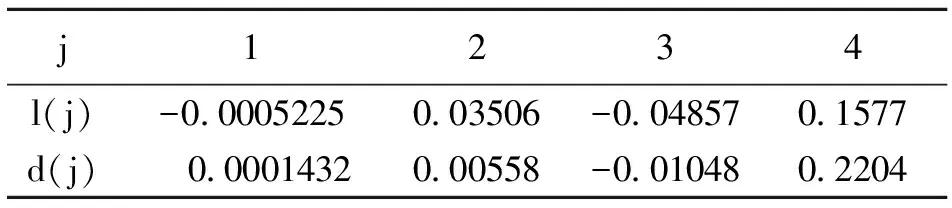
表1 l(j),d(j)的數值Table 1 The value of l(j),d(j)
本文中的大氣密度計算公式用指數大氣模型來近似代替:
ρ=ρ0e-h/H
(4)
式中,ρ0為海平面的大氣密度;高度h=r-R0,R0為地球平均半徑;H為標量高度系數。
1.3 約束條件
(1)終端約束
本文中再入終端約束包括高度、經度、緯度和速度約束,相關約束條件為:
h(tf)=hf,θ(tf)=θf
φ(tf)≥φf,V(tf)≥Vf
(2)熱流、過載、動壓約束
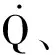
(5)
1.4 優化目標
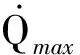
f1=min(tf)
f2=max(δ)=max|φf-φ0|
1.5 軌跡優化問題描述
軌跡優化問題實際上是最優控制問題,在滿足各種約束條件下,尋求使某個指標最優的控制量。高超聲速飛行器再入軌跡優化可以歸結為如下最優控制問題:
(6)
式中,狀態變量X(t)=[r(t),θ(t),φ(t),V(t),γ(t),ψ(t)];控制變量U(t)=[α(t),β(t)];路徑約束為C[X(t),U(t),t]。
偽譜法在求解單目標軌跡優化問題時顯現出很大的優勢。本文采用hp自適應偽譜法作為軌跡尋優方法,hp自適應偽譜法的特點是運算所需時間較短,能夠通過決定在某個網格時間區間中的狀態量和控制量是否滿足特定的偏差來調整當前的計算方式,以達到提高算法精度的目的。如果沒有滿足精度要求,則配置點的數目及分配方式要通過增加多項式的階數或者更新網格來達到精度要求,具體算法參見文獻[6-7]。
2 物理規劃方法概述
2.1 設計思路
物理規劃[1]是Messac提出的一種處理多目標優化設計問題的有效方法,是處理多目標優化問題的新框架。其基本思路是:通過求解單目標優化問題,確定區間邊界,從而建立偏好函數,將不同物理意義的各種設計目標轉換為具有相同數量級的無量綱的綜合滿意度目標,再對綜合滿意度目標進行優化,尋求使其最優的設計點,即為最優解。
2.2 數學模型
物理規劃的決策模型為:
(7)
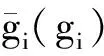
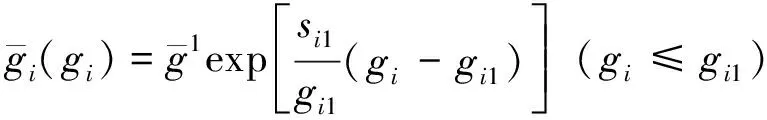
(8)
(9)
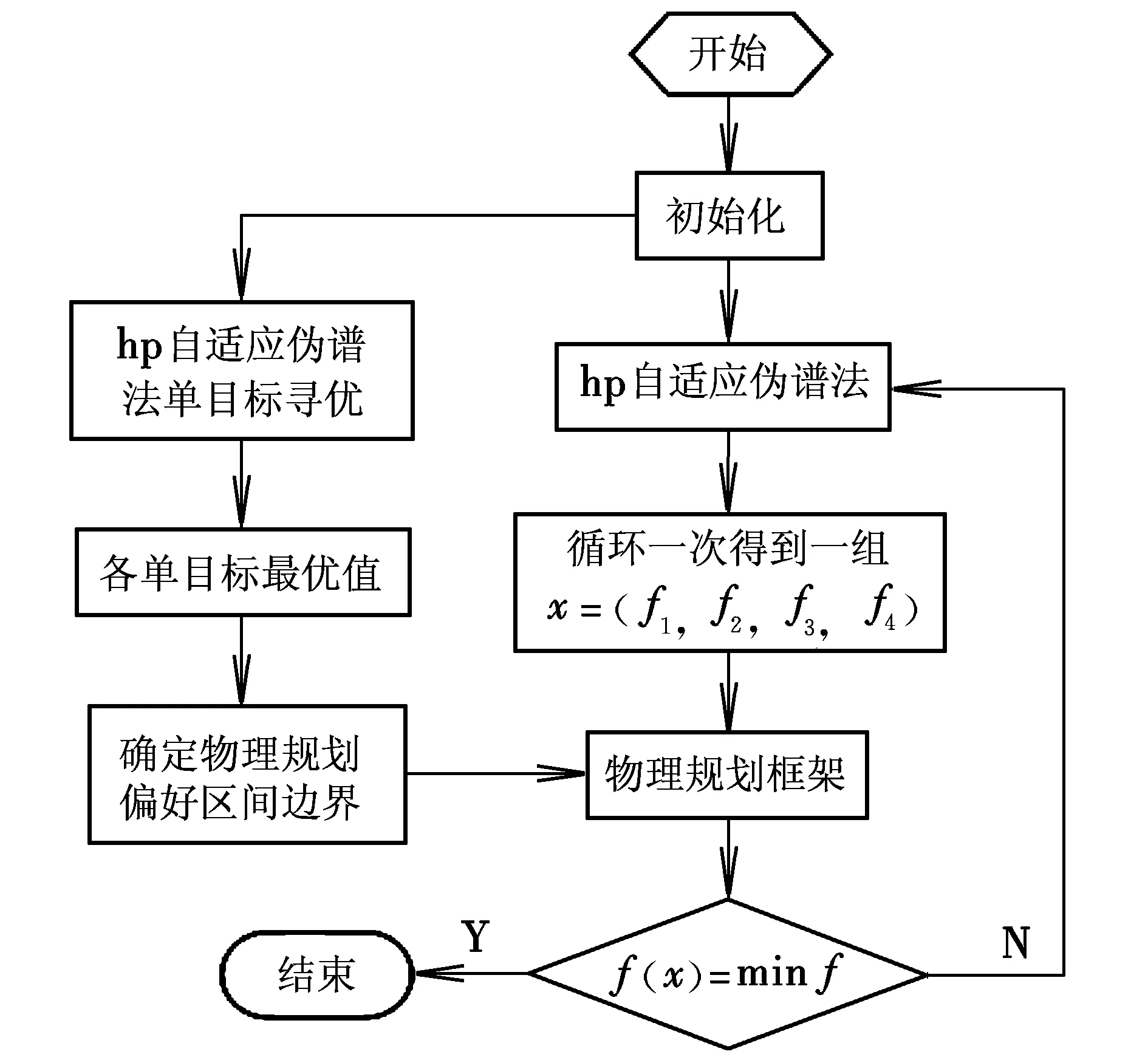
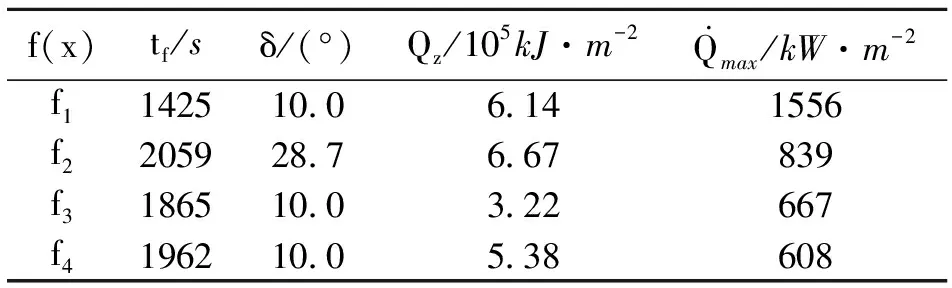
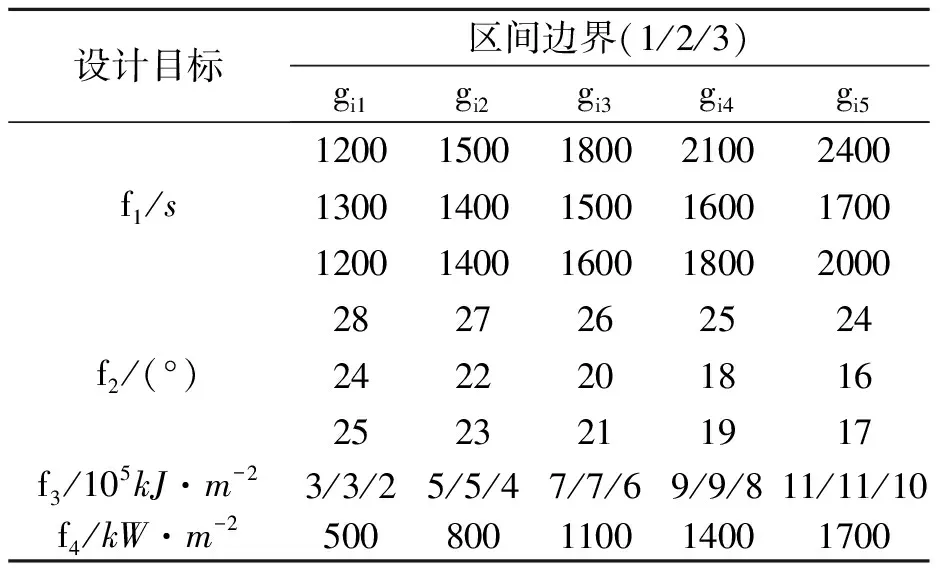
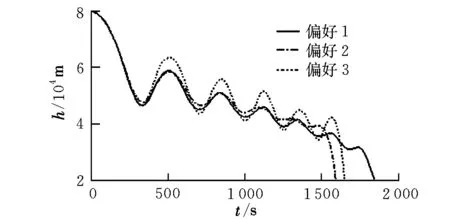
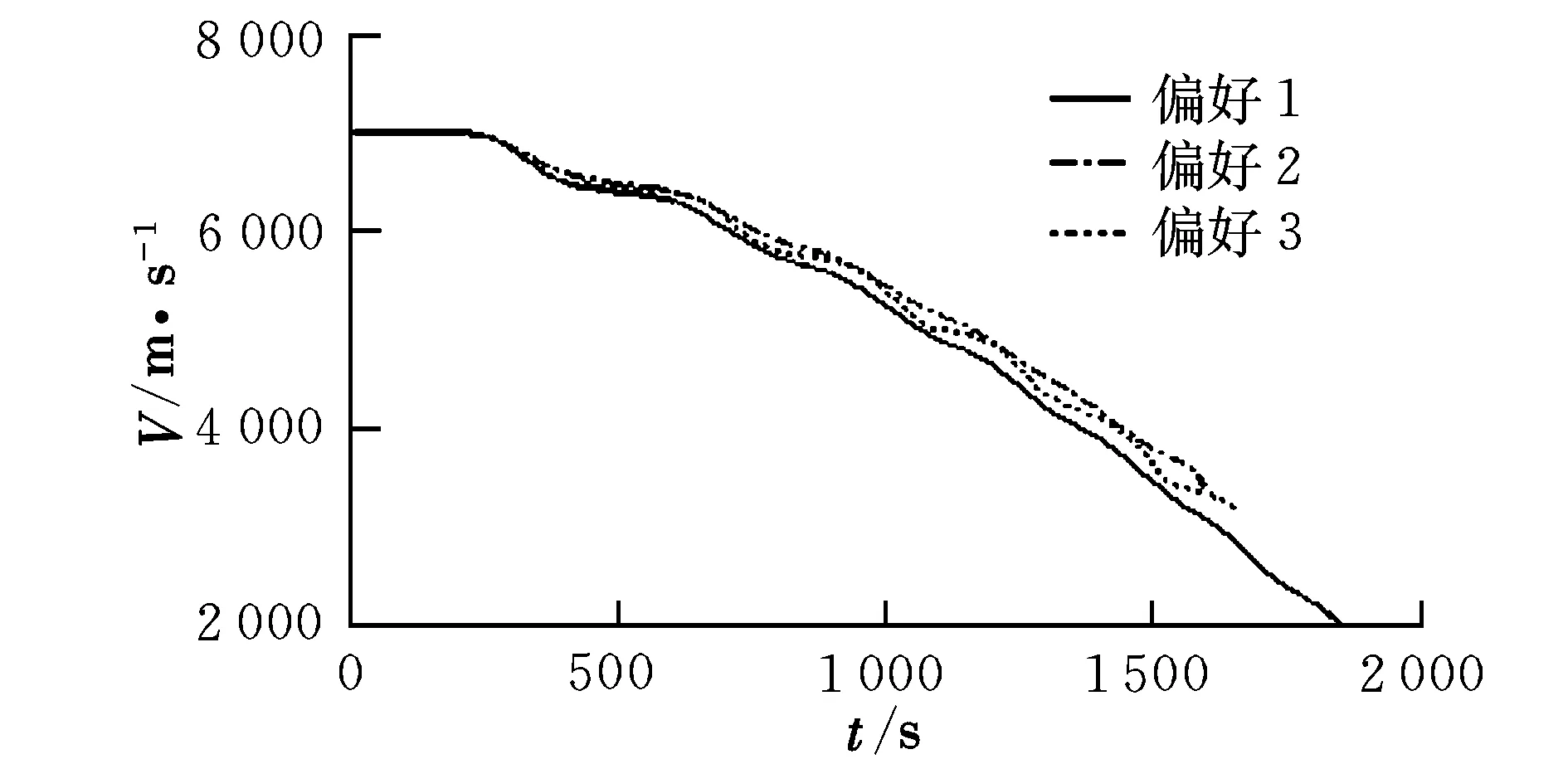
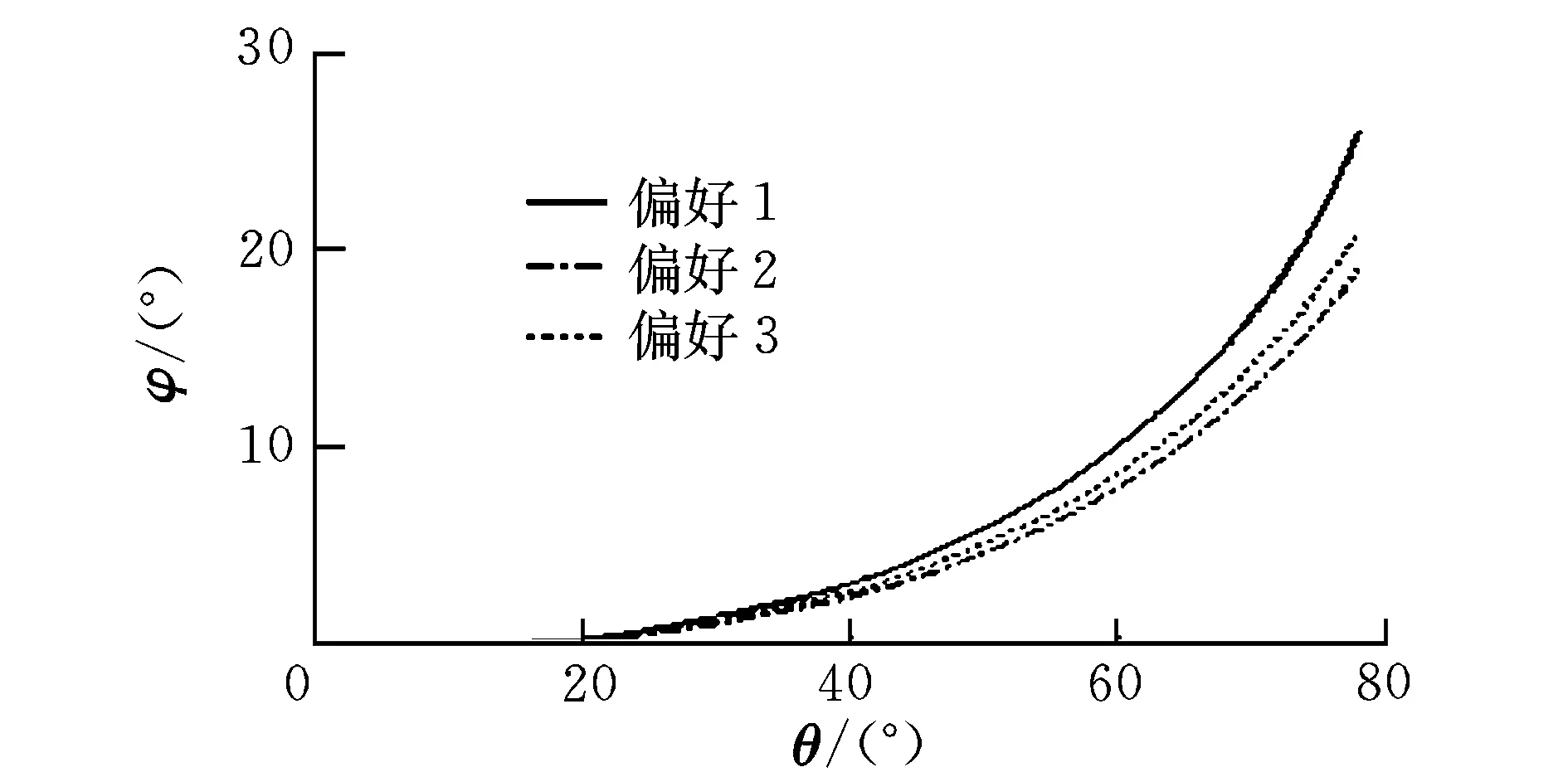
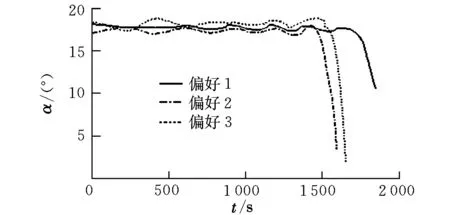
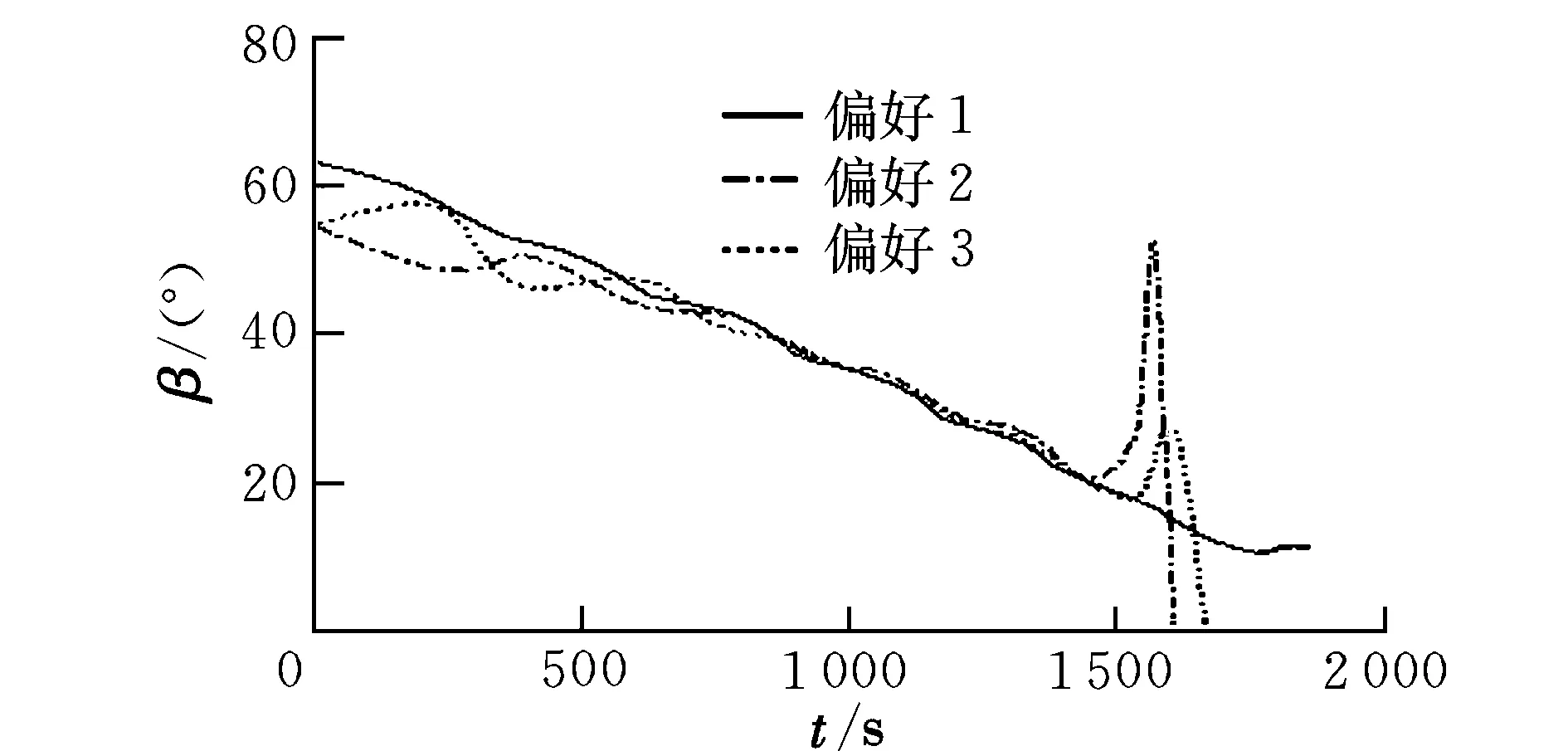
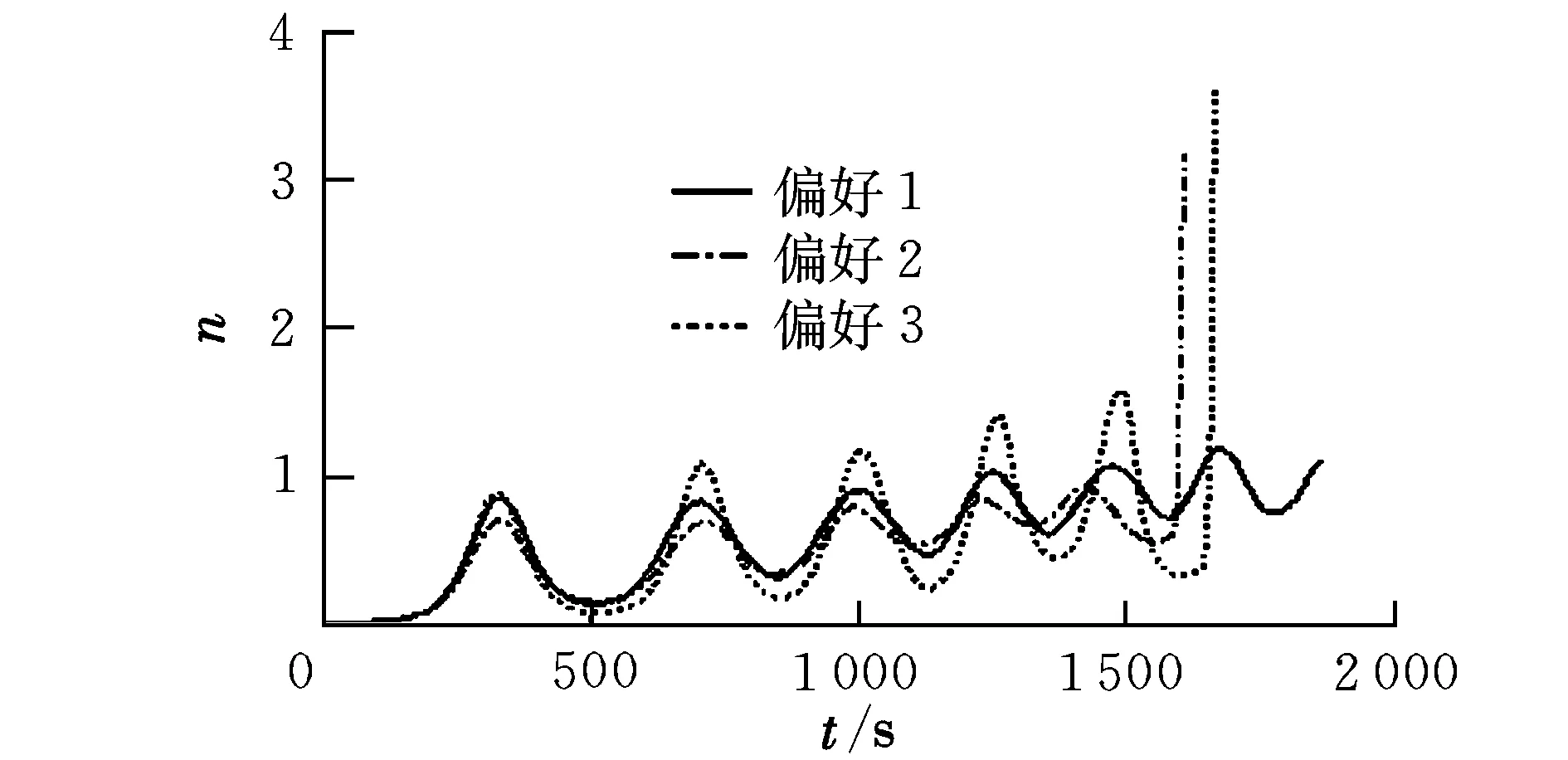
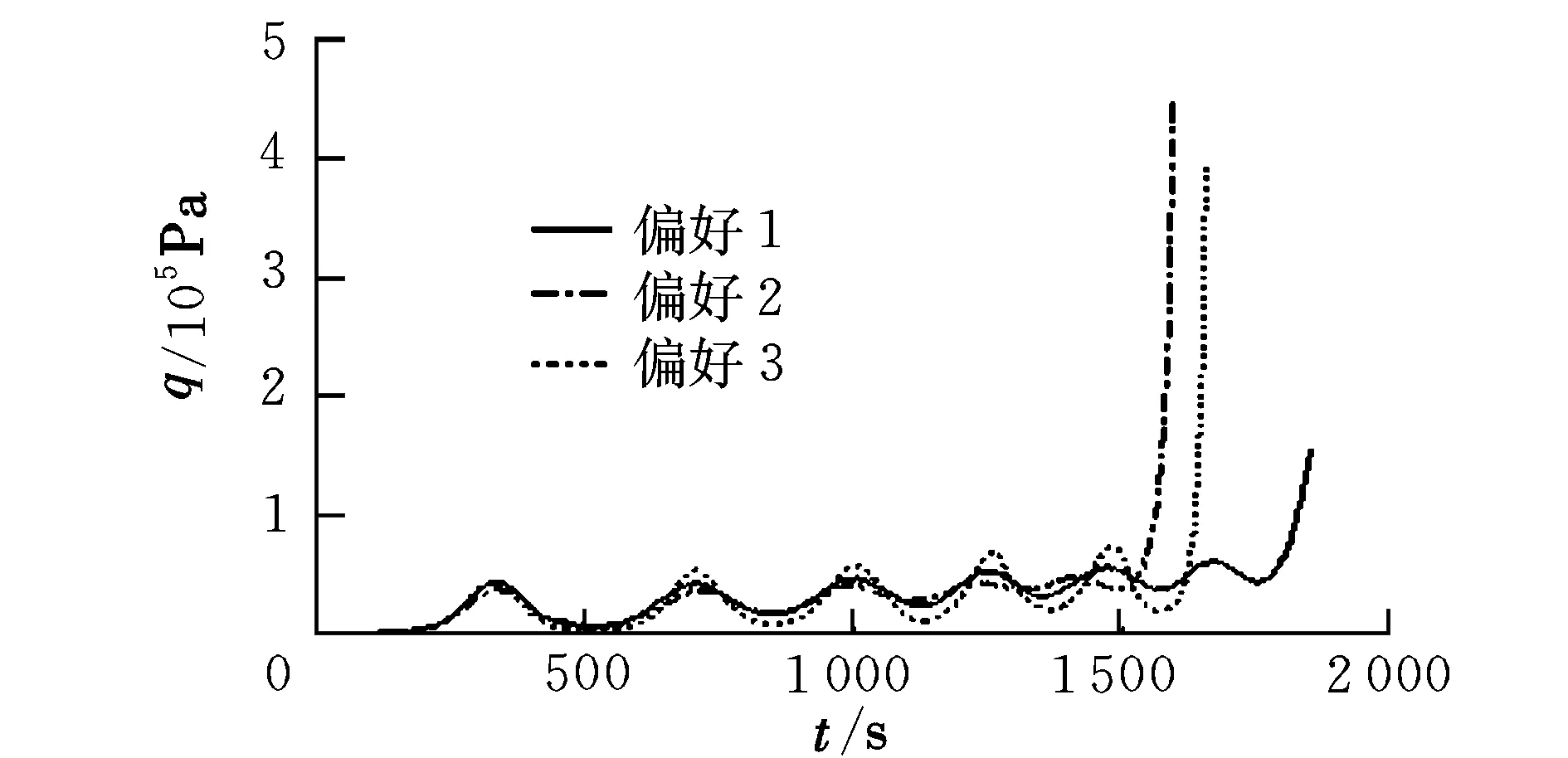
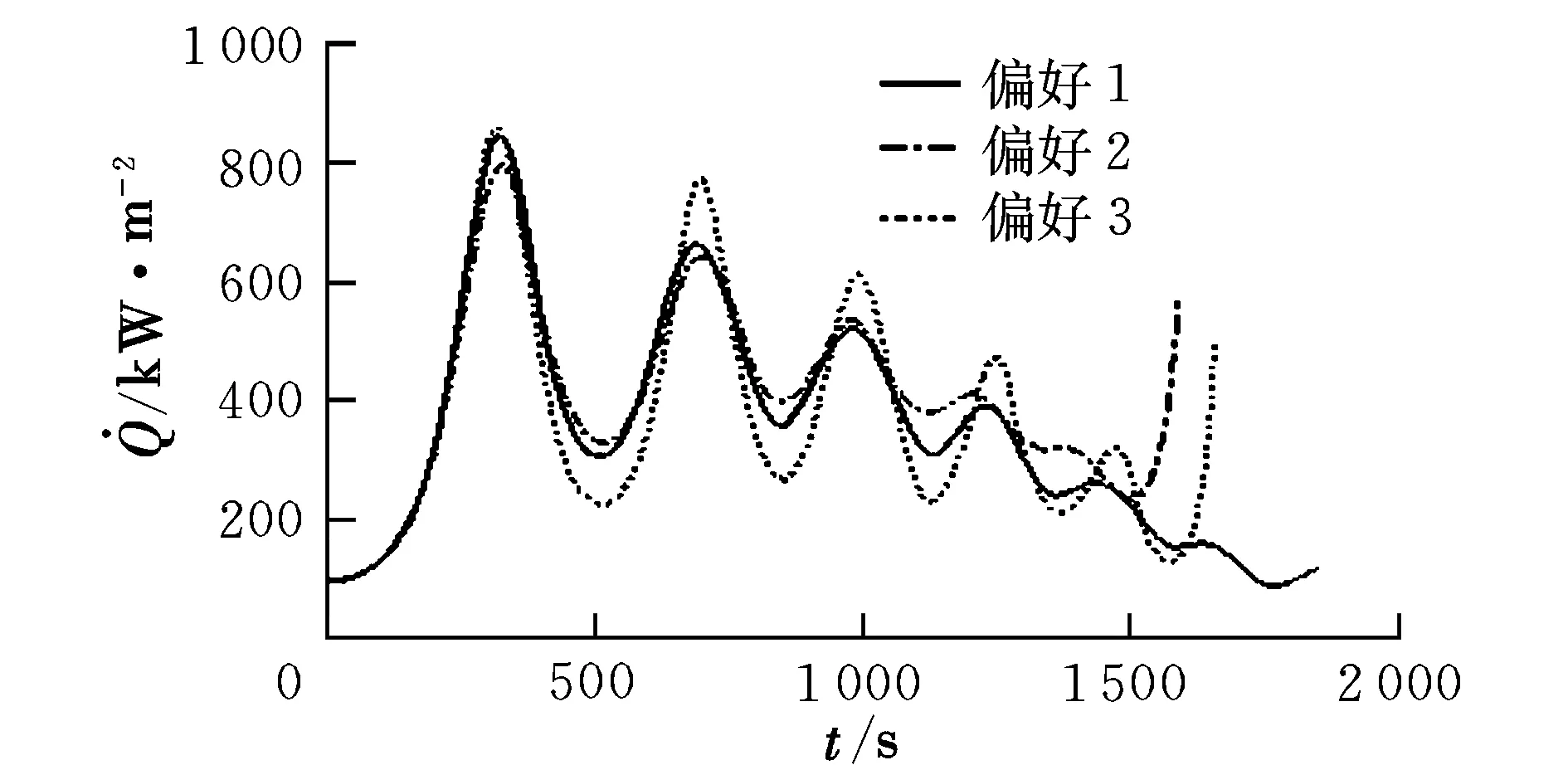
式中,gi(k-1) (10) λik=gik-gi(k-1) (11) (12) (13) (14) (15) 區間端點信息確定方法如下: (16) 構造偏好函數時,需要驗證其是否滿足二階導數嚴格為正的特性,即對區間邊界處的二階導數進行驗證,可由式(17)計算得出。 (17) 其中: (18) (19) 由于0≤ξik≤1,所以只需要驗證a,b是否為正即可[2]。 (20) 由1.4節中確定的優化目標可知,偏好僅為Class1-S型和Class2-S型,其優化模型的綜合滿意度目標為: (21) 首先運用hp自適應偽譜法求解出單目標情況下的最優軌跡,利用得到的各目標參數確定物理規劃偏好區間邊界,建立物理規劃框架。然后將物理規劃優化模型的代價函數作為hp自適應偽譜法的尋優目標進行尋優,即將每次循環得到的各單目標值帶入物理規劃框架,得到綜合滿意度目標,對綜合滿意度目標進行尋優,得到最優解。這樣就將多個目標軌跡優化問題轉換為一個反映設計者偏好的單目標問題。具體流程如圖1所示。 圖1 算法流程圖Fig.1 Flow chart of the algorithm 取飛行器質量m=907 kg,氣動參考面積S=0.48 m2,初始再入點高度h=80 km,初始經度θ0=0°,初始緯度φ0=0°,初始速度V0=7000 m/s,初始航跡角γ0=0°,初始航向角ψ0=0°,設定最終高度hf=20 km,最終經度θf=78°,最終緯度φf≥10°,最終速度Vf≥2000 m/s。 狀態變量及控制變量的約束條件如下: 為確定物理規劃問題的偏好結構,首先求解和分析單目標最優軌跡。運用hp自適應偽譜法,分別以各單目標為優化目標尋優,可得到當滿足某單目標最優時其余目標的數據如表2所示。 表2 單目標最優時其余目標對應值Table 2 Data corresponding to the rest when single objective is optimum 由于再入過程中各中間變量存在著較強的耦合關系,不存在使所有目標同時最優的設計點。通過對其整體分析可以看出,追求單個目標最優時,容易出現其他指標太過局限的情況,實用性不大。 根據相關約束的邊界條件及表2計算結果,確定三組區間邊界不同的偏好結構,記為偏好1,2和3,分別對應于期望橫程較大、再入時間較短和總氣動加熱較小的三組偏好,如表3所示。 表3 多目標軌跡優化的偏好結構Table 3 Preference structure of multi-objective trajectory optimization 為作對比,本文分別采用hp自適應偽譜法和文獻[4]中算法對該問題進行尋優,設定精度為10-5。 (1)優化結果對比 根據表3中的三組偏好結構,采用兩種算法,得到的三組目標函數分別對應橫程較大、再入時間較短、總氣動加熱較小。 本文算法所需運算時間分別為12.32 s,12.20 s,11.79 s。三組偏好函數為: f1=(1854 s,26.0°,6.48×105kJ/m2,844 kW/m2) f2=(1601 s,19.0°,6.49×105kJ/m2,794 kW/m2) f3=(1660 s,21.1°,6.05×105kJ/m2,859 kW/m2) 文獻[4]算法所需運算時間分別為66.47 s,69.55 s,56.06 s。三組偏好函數為: f1=(1842 s,25.9°,6.48×105kJ/m2,846 kW/m2) f2=(1596 s,18.9°,6.48×105kJ/m2,789 kW/m2) f3=(1662 s,21.1°,6.07×105kJ/m2,861 kW/m2) 對比可知,兩種算法所得各組目標函數均能體現出設計者的偏好,且各項設計指標都在可接受的范圍內,是各目標之間相互妥協折中的反映,避免了因追求單個目標最優而出現的其他指標太過局限的情況。但本文算法在所需尋優時間上有明顯優勢,更接近于在線實時規劃;驗證了改進的物理規劃方法的有效性,使其可在不改變約束邊界值的情況下,增大適用范圍。 (2)再入過程分析 對本文算法所得優化結果進行分析,最優軌跡及相應的控制變量、過程約束量如圖2~圖9所示。通過對比分析可以發現: ①在要求總氣動加熱較小時,高超聲速滑翔再入軌跡的振蕩幅值較大,即通過大幅振蕩來減少動能和勢能向熱能的轉換,但此時對飛行器機體結構要求較高。 ②當設計者要求較短時間再入時,飛行器為快速再入到指定高度,在很長一段時間內保持了較大的再入速度;末端迎角快速減小,導致飛行末端動壓較大,同時引起其他變量的一系列大幅調整;對比三組偏好可發現,隨著末端速度的減小,末端動壓逐漸回歸到較好的范圍內。 ③初始下降段一般采用較大的迎角減速,對比圖6可以看出,要求總氣動加熱較小時,初始段迎角平均值較其他偏好大,以增大振蕩幅度;末端迎角大幅變小,以較快進入指定高度。 ④初始段傾側角較大,以快速改變再入方向,增大橫程;隨著速度的減小,傾側角逐漸減小,這是由于要兼顧縱程和再入時間,不能因為追求橫程而使縱程過小或者再入時間太長;末端由于迎角的調整,傾側角有相應的振蕩變化,使末端再入過程滿足過載、熱流等約束。 圖2 高度變化曲線Fig.2 Altitude variation curve 圖3 速度變化曲線Fig.3 Velocity variation curve 圖4 橫程變化曲線Fig.4 Cross-range variation curve 圖5 迎角變化曲線Fig.5 AOA variation curve 圖6 傾側角變化曲線Fig.6 Bank angle variation curve 圖7 過載變化曲線Fig.7 Load variation curve 圖8 動壓變化曲線Fig.8 Dynamic pressure variation curve 圖9 熱流密度變化曲線Fig.9 Variation curve of heat flow density 本文對高超聲速滑翔式再入飛行器三自由度最優軌跡進行了研究,在物理規劃的框架下,對期望橫程較大、再入時間較短以及總氣動加熱較小的三組偏好進行了仿真,驗證了改進的物理規劃方法與偽譜法結合求解多目標優化問題的有效性,得到了反映設計者偏好且實用性更強的三組折中解,所需優化時間相對較短,具有實時應用潛力,可為再入軌跡的優化選擇提供一定借鑒。 參考文獻: [1] Messac A.Physical programming-effective optimization for computational design[J].AIAA Journal,1996,34(1):149-158. [2] 胡丹,閆忠文.基于物理規劃的數據中繼衛星鏈路配置決策方法[J].中國空間科學技術,2009,10(5):54-60. [3] 龍瓊,胡列格,張蕾,等.基于物理規劃的路徑誘導方法[J].中南大學學報(自然科學版),2012,43(8):3287-3293. [4] 雍恩米,唐國金,陳磊.基于物理規劃的高超聲速飛行器滑翔式再入軌跡優化[J].航空學報,2008,29(5):1091-1097. [5] Bollino Kevin P,Michael Ross,Doman David D.Optimal nonlinear feedback guidance for reentry vehicles[R].AIAA-2006-6074,2006. [6] Darby C L,Hager W W,Rao A V.An hp-adaptive pseudospectral method for solving optimal control problems[J].Optimal Control Applications and Methods,2011,32(4):476-502. [7] 國海峰,黃長強,丁達理,等.多約束條件下高超聲速導彈再入軌跡優化研究[J].彈道學報,2013,25(1):10-15.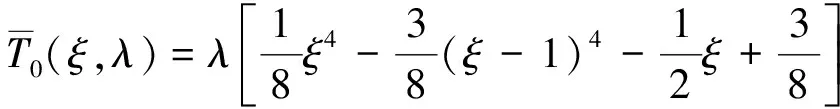
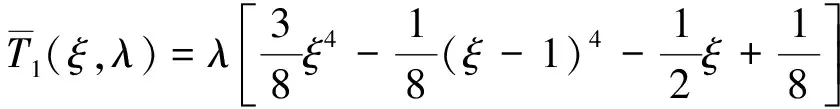
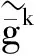
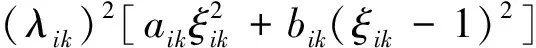
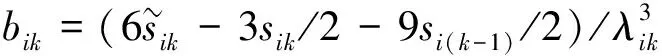
2.3 算法改進
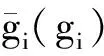

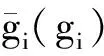
3 算法流程
4 仿真結果及分析
4.1 初始條件
4.2 偏好結構的確定
4.3 優化結果及分析
5 結束語

