三維Hom-Leibniz超代數的分類
馬鳳敏,張永平,董 蕾,張慶成
(1.河北工業職業技術學院基礎部,河北 石家莊 050000;2.沈陽化工學院數學系,遼寧 沈陽 110142;3.東北師范大學數學與統計學院,吉林 長春 130024)
Leibniz代數最早是由A.Bloch在文獻[1]中涉及的,當時稱為D-代數,直到20世紀90年代,J.L.Loday在研究不滿足交錯性的廣義李代數時,正式提出這個概念[2].對于非李代數的Leibniz代數的研究,一直是許多學者的努力方向,在非李代數的Leibniz代數分類問題上,已經完成了對二維、三維以及四維冪零的分類[3],在Leibniz代數其他方面的研究主要集中在關于同調問題等抽象理論上[4].
代數形變理論最早由 M.Gerstenhaber提出[5],Hom-代數是代數形變理論中的一類,文獻[6-9]引入了Hom-代數的概念,并進行了系統的研究.對Hom-代數的分類,也是研究的一個重要內容,本文在對三維非李代數的Leibniz超代數的分類基礎上[10],研究三維非李超代數的Hom-Leibniz超代數的分類.通過偶自同態定義,運用待定系數法,得到系數的矩陣乘法表.
1 Hom-Leibniz超代數
定義1.1[1]設L是一個向量超空間:[·,·]是L×L→L的一個雙線性映射,α是L→L的一個超空間偶自同態映射,滿足:

則稱(L,[·,·],α)是一個 Hom-Leibniz超代數.
定理1.1 若(L,[·,·])是一個Leibniz超代數,α:L→L是一個偶的Leibniz超代數的同態映射,則(L,[·,·]α,α)構成一個 Hom-Leibniz超代數,其中[·,·]α=[α(x),α(y)].
證明 顯然α關于括積[·,·]α構成超代數間的同態映射,我們只需證明?x,y,z∈L,滿足Hom-Leibniz超等式.
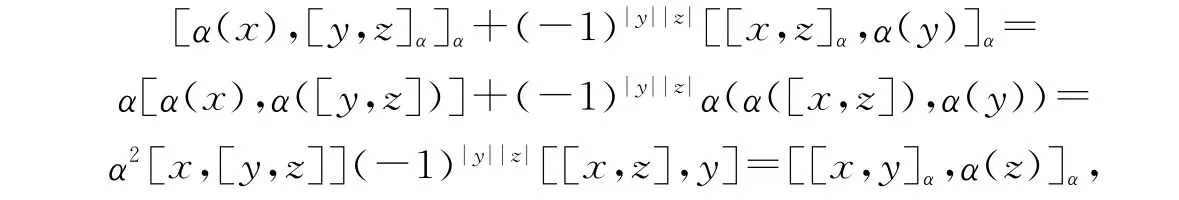
則(L,[·,·]α,α)構成一個 Hom-Leibniz超代數.
設(L,[·,·])是一個Leibniz超代數,α是L的一個偶的自同態映射,即

設e0,e1,e2是L 的齊次基,則

利用
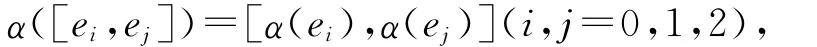
確定α(e0),α(e1),α(e2)的表達系數Lkl,k=0,1,2;j=1,2,3.從而確定偶自同態α的表示矩陣

2 Hom-Leibniz超代數的分類
利用文獻[10]中三維Leibniz超代數的分類結果,應用定理1.1知,當α是Leibniz超代數L的一個偶自同態時,(L,[·,·]α,α)構成一個 Hom-Leibniz超代數.因此,我們可以通過待定系數法,對偶自同態α進行分類,從而完成對Hom-Leibniz超代數的分類.


證明 應用文獻[10]中分類的結果.

表示成矩陣為


對應的矩陣為:

對應的矩陣為:

由方程的對稱性,可以得到L01=L11,L02=L12或L01=L12,L02=L11.
當k=0時,
① 當L01=L11,L02=L12時,得+=0,即L01=L11=L02=L12=L23=0.
② 當L01=L12,L02=L11時,L01L02+L02L01=0,則L01L02=0.

當k≠0時,

當L01=L12,L02=L11時,

即當k=0時,

對應的矩陣為:

當k≠0時,

對應的矩陣為:

對應的矩陣為:

對應的矩陣為:

解上述方程組,當k≠0時,

對應的矩陣為:
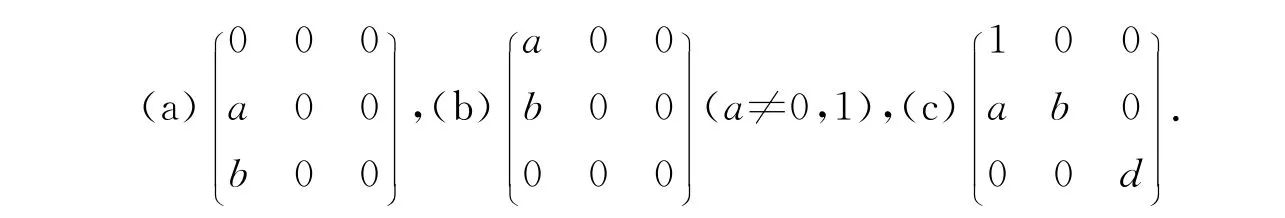
當k=0時,

對應的矩陣為:

對應的矩陣為:

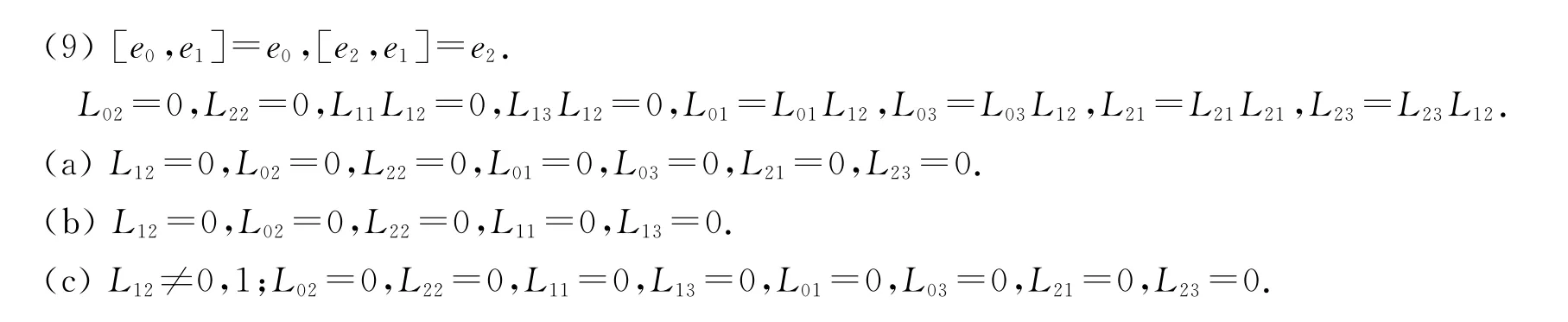
對應的矩陣為:

對應的矩陣為:

解上述方程組,當k=0時,

對應的矩陣為:

當k=1時,無解.
當k≠0,1時,

對應的矩陣為:

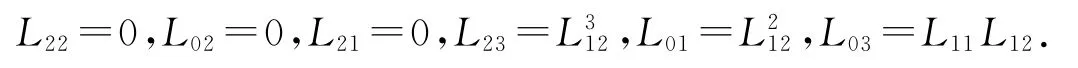
對應的矩陣為

(13)[e1,e2]=e0+e1,[e0,e2]=ke1.
當k=0時,L01+L11=L12L23,L02+L12=L12L23,L03+L13=0,L02L23=0.

對應的矩陣為:

當k≠0時,L13=0,L03=0,L01+L11=L12L23,L02+L12=L12L23+kL11L23,kL11=L02L23,L02L23+kL01L23=kL12.
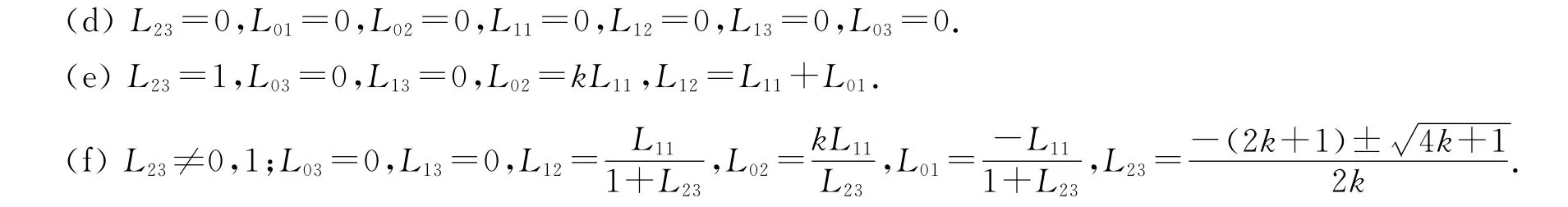
對應的矩陣為:

應用類似的方法可得下列結果:

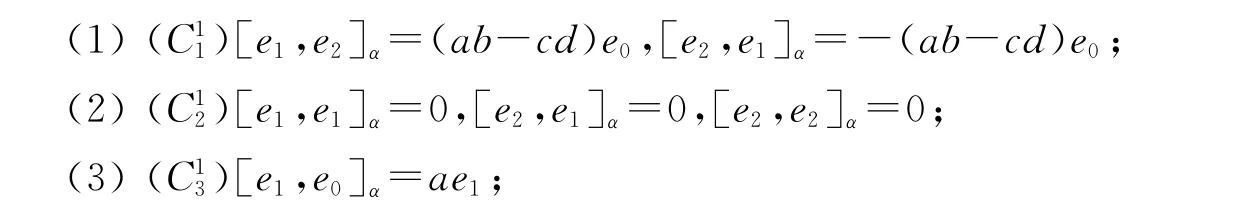
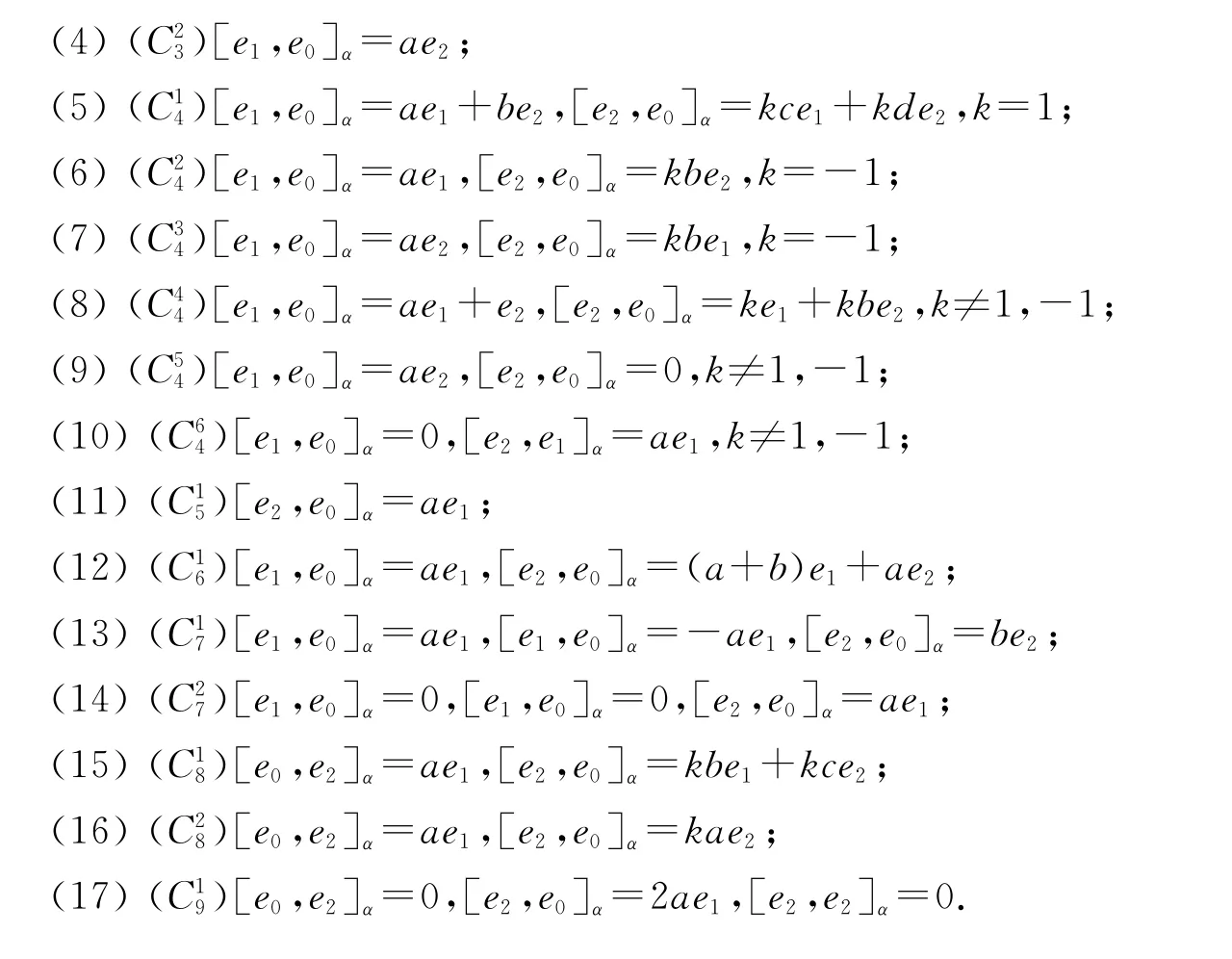
[1]BLOCH A.On a generalization of Lie algebra[J].Math IUSSR Doklady,1965,163(3):471-473.
[2]LODAY J L.Une version non commutative des algebras de Lie:les algebra de Leibniz[J].Enseign Math Ann,1993,296(1):139-158.
[3]蔣啟芬.三維Leibniz代數的分類[J].數學研究與評論,2007,27(4):677-686.
[4]劉東.無限維Lie代數和Leibniz代數[D].上海:華東師范大學,2004.
[5]GERSTENHABER M.On the deformation of rings and algebras[J].Ann Math,1964,79(1):59-103.
[6]LARSSON D,SILRESTROV S D.Quasi-Hom-Lie algebras,central extensions and 2-Cocycle-Like indentities[J].J Algebra,2005,288(2):321-344.
[7]MAKHLOUF A,SILVESTROV S D.Hom-algebra structure[J].J Gen Lie Theory Appl,2008,2(2):51-64.
[8]HARGWIT J T,LARSSON D,SILRESTROV S D.Deformation of Lie algebras usingσ-derivations[J].J Algebra,2006,295(2):314-361.
[9]FAOUZI AMMAR.Cohomology of Hom-Lie superalgebras and q-deformed Witt superalgebra[J/OL].[2012-04-27].http://arxiv.org/pdf/1204.6244.pdf.
[10]王衛國.低維Leibniz超代數的分類[D].上海:華東師范大學,2007.

