邊故障k元n立方體的超級哈密頓交織性

張淑蓉，王世英，董操

山西大學數學科學學院，太原 030006

邊故障k元n立方體的超級哈密頓交織性

張淑蓉，王世英，董操

山西大學數學科學學院，太原 030006

k元n立方體（記為）是優于超立方體的可進行高效信息傳輸的互連網絡之一。是一個二部圖當且僅當k為偶數。令G[V0，V1]是一個二部圖，若（1）任意一對分別在不同部的頂點之間存在一條哈密頓路，且（2）對于任意一點v∈Vi，其中i∈{0，1}，V1-i中任意一對頂點可以被G[V0，V1]-v中的一條哈密頓路相連，則圖G[V0，V1]被稱為是超級哈密頓交織的。因為網絡中的元件發生故障是不可避免的，所以研究網絡的容錯性就尤為重要。針對含有邊故障的，其中k≥4是偶數且n≥2，證明了當其故障邊數至多為2n-3時，該故障是超級哈密頓交織圖，且故障邊數目的上界2n-3是最優的。

互連網絡；超級哈密頓交織性；k元n立方體

1 引言和基本概念

隨著計算機應用的不斷深入，迫切需要速度更快，性能更高的計算機系統，進而開辟了并行和分布式系統的研究領域。系統中元件之間的連接模式稱為該系統的互連網絡，或者簡稱為網絡。毫無疑問，并行和分布式系統功能的實現在很大程度上依賴于該系統的互連網絡結構。k元n立方體是最重要的互連網絡之一[1-4]。它具有許多優良性質，如易運行，低延遲和高帶寬。正是這些優良的性質，k元n立方體受到了廣泛關注，并且大量的并行和分布式系統都是基于k元n立方體來形成其連接模式，如iWarp[5]，J-machine[6]和IBM Blue Gene/L[7]。

互連網絡可以看成一個圖G=(V(G)，E(G))，其中V(G)和E(G)分別表示G的頂點集和邊集。圖的頂點表示系統中的元件，圖的邊表示元件之間的物理連線。在G中，頂點u的所有鄰點組成的集合稱為u的鄰域，記作NG(u)。若G的頂點可以被劃分為兩個集合V0和V1，使得每條邊的端點一個在V0中，另一個在V1中，則稱圖是二部圖，這樣的一個分劃(V0，V1)被稱為是圖G的一個二分劃，V0和V1被稱為是圖的兩個部。若二部圖中任意一對分別在不同部的頂點之間存在一條哈密頓路，則稱該圖是哈密頓交織圖[8]。

設G是具有二分劃(V0，V1)的哈密頓交織圖。若Vi中任意一對頂點可以被G中的一條長度為|V(G)|-2的路相連，則圖G被稱為是強哈密頓交織圖[9]。對于任意一點v∈Vi，其中i∈{0，1}，V1-i中任意一對頂點可以被G-v中的一條哈密頓路相連，則圖G被稱為是超級哈密頓交織圖[10]。

由以上定義可以看出，若G是超級哈密頓交織圖，則G一定是強哈密頓交織圖。

在實際應用中，網絡中的元件或連線也可能發生故障從而影響到網絡的正常運行，所以研究故障網絡的（強或超級）哈密頓交織性具有重要的意義[11-13]。

Huang在2009年[9]已經證明了當k為偶數時，不含故障邊的k元n立方體是強哈密頓交織圖。而本文是在文獻[9]的基礎上所做的進一步研究，并且證明了：至多含有2n-3條故障邊的k元n立方體（k為偶數）是超級哈密頓交織圖，可見該結果推廣并涵蓋了文獻[9]的主要結論。

定義1（m-邊容錯（超級）哈密頓交織圖）設G是二部圖，F(|F|≤m)是G的故障邊集合。若G為（超級）哈密頓交織圖且G-F仍為（超級）哈密頓交織圖，則稱G是m-邊容錯（超級）哈密頓交織圖。

定義2（k元n立方體）k元n立方體，記為(k≥1， n≥1)，是一個具有kn個頂點的圖，每個頂點可以標記為u=un-1un-2…u0，其中ui∈{0，1，…，k-1}，0≤i≤n-1。兩個頂點u=un-1un-2…u0和v=vn-1vn-2…v0相鄰當且僅當存在一個整數j∈{0，1，…，n-1}，使得uj=vj±1 (mod k)且對每個i∈{0，1，…，n-1}{j}都有ui=vi。這樣的邊uv被稱為是一條j維邊。為書寫方便，在本文中遇到類似情況時省略“(mod k)”。

取定一個正整數j∈{0，1，…，n-1}。刪除所有的j維邊便可以沿第j維將(k≥2)劃分為k個不相交的子立方，依次記為：0]，[1]，…，[k-1]（在不引起歧義的情況下，簡記為Q[0]，Q[1]，…，Q[k-1]，如圖1）。顯然對每一個0≤i≤k-1，Q[i]均與同構。在該中任取一點u=uu…uuu…u，不失一般n-1n-2j+1jj-10性，假設u∈V(Q[i])，其中0≤i≤k-1。記Q[i′]中的頂點v=un-1un-2…uj+1vjuj-1…u0為ni′(u)，其中vj≠uj。可以看出ni′(u)和u相鄰當且僅當i′=i±1。

圖1 將劃分為Q[0]，Q[1]，…，Q[k-1]

圖3 的子圖Row[0:3]

圖2 的子圖Row[0:2]

2 主要結論

首先給出對主要結論證明有用的一些引理。

引理2.1[14]在Row[0:p]中任取3個不同的頂點s，t和x，其中1≤p≤k-1。若δ(x，s)=1且δ(s，t)=0，則Row[0:p]-x中存在一條哈密頓st-路。

引理2.2[15]設n≥2是整數，k≥4是偶數。在中任取兩個相鄰頂點s*和t*，則-{u*，v*}是哈密頓交織圖。

引理2.3[16]若n≥2是整數，k≥4是偶數，則是(2n-2)-邊容錯哈密頓交織圖。

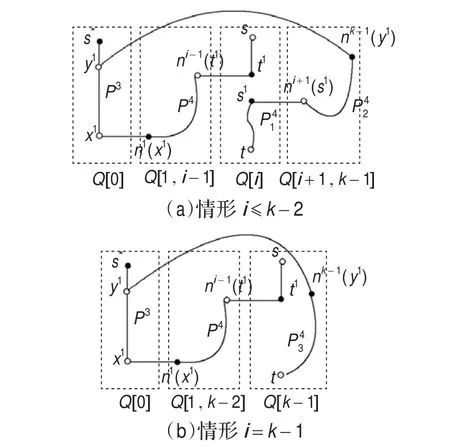
圖4 情形1.1.1中哈密頓路的構造方法演示

圖5 情形1.2.1中哈密頓路的構造方法演示

圖6 情形2中哈密頓路的構造方法演示

3 結束語

本文主要對含有故障邊的k元n立方體（k≥4為偶數）的超級哈密頓交織性進行了研究。證明了若該k元n立方體中的故障邊集F滿足|F|≤2n-3，則-F是超級哈密頓交織圖。這一結果表明，就超級哈密頓交織性來說，k元n立方體（k≥4為偶數）具有良好的故障容錯能力，這一結果對于建立k元n立方體（k≥4為偶數）環境下的T比特路由器是不無裨益的。

[1]Bose B，Broeg B，Younggeun K，et al.Lee distance and topological properties of k-ary n-cubes[J].IEEE Transactions on Computers，1995，44（8）：1021-1030.

[2]Dally W J.Performance analysis of k-ary n-cube interconnection networks[J].IEEE Transactions on Computers，1990，39（6）：775-785.

[3]Ghozati S A，Wasserman H C.The k-ary n-cube network：modeling，topological properties and routing strategies[J]. Computers and Electrical Engineering，1999，25（3）：155-168.

[4]Hsieh S Y，Chang Y H.Extraconnectivity of k-ary n-cube networks[J].Theoretical Computer Science，2012，443（20）：63-69.

[5]Peterson C，Sutton J，Wiley P.iWarp：a 100-MOPS，LIW microprocessor for multicomputers[J].IEEE Micro，1991，11（3）：26-29，81-87.

[6]Noakes M，Dally W J.System design of the J-machine[C]// 6th MIT Conference on Advanced Research in VLSI，1990：179-194.

[7]Adiga N R，Blumrich M A，Chen D，et al.Blue Gene/L torus interconnection network[J].IBM Journal of Research and Development，2005，49（2）：265-276.

[8]Wong S A.Hamiltonian cycles and paths in buttery graphs[J]. Networks，1995，26（3）：145-150.

[9]Huang C H.Strongly Hamiltonian laceability of the even k-ary n-cube[J].Computers and Electrical Engineering，2009，35（5）：659-663.

[10]Lewinter M，Widulski W.Hyper-Hamilton laceable and caterpillar-spannable product graphs[J].Computers and Mathematics with Applications，1997，34（11）：99-104.

[11]Li T K，Tan J J M，Hsu L H.Hyper hamiltonian laceability on edge fault star graph[J].Information Sciences，2004，165（1/2）：59-71.

[12]Tsai C H，Tan J J M，Liang T，et al.Fault-tolerant Hamiltonian laceability of hypercubes[J].Information Processing Letters，2002，83（6）：301-306.

[13]Araki T，Kikuchi Y.Hamiltonian laceability of bubblesort graphs with edge faults[J].Information Sciences，2007，177（13）：2679-2691.

[14]Kim H C，Park J H.Fault hamiltonicity of two-dimensional torus networks[C]//Workshop on Algorithms and Computation，Tokyo，Japan，2000：110-117.

[15]Wang Shiying，Zhang Shurong.Embedding hamiltonian paths in k-ary n-cubes with conditional edge faults[J]. Theoretical Computer Science，2011，412（46）：6570-6584.

[16]Stewart I A，Xiang Yonghong.Embedding long paths in k-ary n-cubes with faulty nodes and links[J].IEEE Transactions on Parallel and Distributed Systems，2008，19（8）：1071-1085.

ZHANG Shurong,WANG Shiying,DONG Cao

School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China

Thek-aryn-cube,denoted by,as one of the most efficient interconnection networks for information

transportation,has been shown as an alternative to the hypercube.Ais bipartite if and only ifkis even.A bipartite graphG[V0，V1]is called hyper hamiltonian laceable if（1）it has a hamiltonian path between any pair of vertices in different parts,and（2）for any vertexv∈Vi,there is a hamiltonian path ofG[V0，V1]-vbetween any two vertices inV1-i,where i∈{0，1}.Since edge faults may occur after a network is activated,it is important to solve problems in faulty networks. This paper addresses the faultywith evenk≥4andn≥2,and proves that thewith at most2n-3faulty edges is hyper hamiltonian laceable.This result is optimal to the number of edge faults tolerated.

interconnection networks;hyper hamiltonian laceability;k-aryn-cubes

A

O157.5

10.3778/j.issn.1002-8331.1212-0216

ZHANG Shurong,WANG Shiying,DONG Cao.Hyper hamiltonian laceability of k-ary n-cubes with edge faults. Computer Engineering and Applications,2014,50（21）：39-43.

國家自然科學基金（No.61070229）；教育部高等學校博士點專項基金（No.20111401110005）。

張淑蓉（1984—），女，博士研究生，研究領域為圖論及其應用；王世英（1961—），男，博士，教授，研究領域為圖論及其應用；董操（1983—），男，碩士研究生，研究領域為圖論及其應用。E-mail：zhangsr@sxu.edu.cn

2012-12-18

2013-07-09

1002-8331（2014）21-0039-05

CNKI出版日期：2013-08-05，http://www.cnki.net/kcms/detail/11.2127.TP.20130805.0943.004.html