造船監理員調度模型和混合遺傳算法求解

符昊，葛洪偉，邵長魯，朱亮

江南大學物聯網工程學院，江蘇無錫 214122

造船監理員調度模型和混合遺傳算法求解

符昊，葛洪偉，邵長魯，朱亮

江南大學物聯網工程學院，江蘇無錫 214122

有效快速地調度不同專業的造船監理員至不同廠區進行監理工作可以提高船舶建造效率，確保船只建造質量。針對我國造船監理公司監理員調度方面缺乏通用模型和調度手段落后的問題，建立起帶有一系列硬性約束和軟性約束的數學模型。隨后針對該數學模型采用了基于模擬退火遺傳算法的混合遺傳算法進行求解。模擬仿真實驗表明該模型與算法取得了理想效果。

造船監理員調度；船舶建造；人員調度；混合遺傳算法；NP問題

1 引言

我國作為全球最大的造船國，據初步統計，在2011年度中國全年造船完工量約為6 800萬載重噸，占全球份額的42.5%。這為我國造船業下一步技術創新和產業升級打下了良好的基礎。由于船舶建造的工藝復雜，耗資巨大，施工的周期長，對其建造過程進行監理就成為必不可少的環節[1]。通常船東會委托監理公司進行船舶建造的監理工作以確保船舶建造質量。監理人員涵蓋船舶建造中所涉及的各類專業，分別有船體、船機、船電和特殊專業工程技術人員，這里的特殊專業工程技術人員是根據船舶的主要工作性能來決定的[2]。為滿足不同廠區在船舶建造過程中對不同專業造船監理員需求的變更，監理公司需要在船舶建造的每個階段對公司內的各專業監理員重新合理調度。每個廠區對各專業監理員數量的需求和調度開銷少這些硬性約束是每次調度應當滿足的。為實現調度的人性化，監理員之間的默契程度以及他們對廠區的偏好這些軟性約束也應予以關注。因此造船監理員調度問題是較為復雜的組合優化問題，屬NP問題。

迄今為止，監理公司調度監理員的方式依舊是傳統的手工調度。這樣調度效率較低，人工成本高，考慮的方面有限，往往不能很好地滿足實際的需求；尤其是在待調度人員人數多、調度情況復雜的時候，人工調度難以實施；所以利用計算機實現自動化調度是未來發展的目標。關于人員分配和調度的組合優化的問題，國外起步較早，研究較多。近年來，如Sabar、Montreuil和Frayret對裝配中心員工調度的研究[3-4]、Ozgur等人對產業部門人員分配的探究[5]以及Ruibin等人對護士排班問題的研究[6-7]等等已研制出多種基于軟計算的方法。但國外為相關問題建立的模型有較強的西方國家特點，與國內管理存在差異。我國對這方面問題的研究起步較晚。直到近年國內才出現例如任守綱等人從我國軟件開發企業角度針對軟件項目人力資源調度的研究[8]；沈吟東等人針對護士排班問題采用貼合實際護士排次類型和排班約束建立適應中國國情的問題模型[9-10]等。但他們考慮的問題較為簡單，算法執行效率也有待改進。

針對造船監理員調度的研究至今國內、外鮮有報道。對于造船業，有獨特的行業特殊性，如果只是簡單地套用其他行業的相關研究則難以滿足企業需求。本文通過對國內造船業現狀的了解分析，考慮了對于造船業具有普遍適應性的監理員調度問題。在同時考慮硬性和軟性約束的基礎上，建立了一個適應我國造船監理公司監理員調度問題的整數規劃（ILP）模型。并針對此問題采用了模擬退火遺傳算法進行仿真實驗求解，實現了對模型和求解算法的驗證。

2 造船監理員調度問題描述

本文研究的造船監理員調度問題是指：給定一個調度周期內的全部可調度的造船監理員及每名監理員掌握的專業；給定在該周期內全部廠區對各專業監理員的需求數目。要求在基本滿足所有廠區所需監理員數目的情況下（考慮到現實中臨時員工的存在，允許出現需求數目超出可調度監理員數目的情況），編制出一個最有效（即滿足硬性約束和軟性約束）的造船監理員調度方案。為了方便管理并且考慮到“一人多專”的情況，要對不同專業的監理員進行統一調度，因此使得該問題變得復雜。

根據船舶建造監理的普遍特性，本文設定：

每名監理員在一個調度周期內只允許調度一次；每名監理員掌握的專業在一個調度周期內是固定不變的；對每名監理員的調度都應以滿足廠區對特定專業監理員數量需求為前提；調度應考慮每名監理員的地域偏好和他們之間的人際關系。

假設一個調度周期為一個月，對于給定n名造船監理員的一個調度方案可以用一張二維表格表示（見表1）。其中第一行表示監理員的編號，第二行表示該監理員被派遣去往的廠區編號。

表1 2012年5月XX船舶建造監理公司員工調度方案

如表1中的方案滿足設定的要求，則為可行方案，否則為不可行方案。同時，要找出可行方案中開銷最少的最佳方案。

3 造船監理員調度問題建模

針對上述從實際工作中提煉出的造船監理員調度問題，首先建立一個考慮硬性約束的整數規劃（ILP）模型，然后建立更人性化的擴展模型，使其能夠反映造船監理員間配合默契程度以及他們對工作地點的偏好。

假設在一個調度周期內共有n位造船監理員，掌握μ類專業，共含有m個廠區。記E={1，2，…，n}表示造船監理員集合。F={1，2，…，m}表示該船舶建造公司擁有的廠區的集合。njk表示第j號廠區對掌握第k號專業造船監理員的需求數量。T是一個n×m的矩陣，tij代表第i號造船監理員前往第j號工廠所耗差旅費；O是表示造船監理員所屬專業的矩陣，oij=1表示造船監理員i掌握第j號專業，否則等于0。調度決定變量xij定義為：

基于以上的記號，建立造船監理公司監理員調度問題的ILP模型如下：

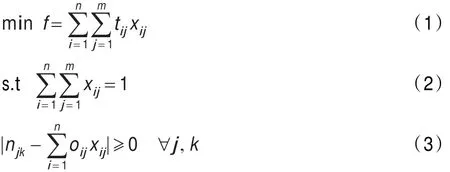
在組合優化問題中，采用罰函數和獎勵函數是一種可行且非常流行的方法。這種方法的思想是將有約束的優化問題通過在目標函數中引入罰函數或者獎勵函數來對破壞約束的情形進行懲罰或者對滿足約束的情形進行獎勵，從而將原目標問題轉化成沒有約束的組合優化問題。轉化后的目標函數格式一般為：

其中λ是與懲罰函數或獎勵函數相關的系數，φ(gπ(X))用來評判破壞約束或者滿足約束的程度。因此，對于本文要研究的問題中的硬性約束，可以使用獎勵函數解決。

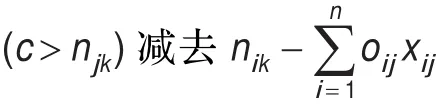
即要研究的只考慮硬性約束時的目標函數。由于每名監理工將作為特定單一專業工種的單位進行調度以滿足實際需求，所以在求解本目標函數過程中對于掌握多種專業技能的監理員會自動淘汰其不大滿足調度需求的專業，保留其最佳專業進行調度。

為了使得調度人性化，下面將進一步考慮監理員之間默契程度和監理員對工作地點的偏好，建立一個造船監理員調度問題擴展模型。

在日常生活工作中，監理員之間的默契程度并非一致。有些監理員之間配合默契，工作效率高；相反，有些監理員之間關系不佳，在一起共事可能會造成不必要的損失。監理員間配合默契程度是衡量不同監理員分配在同一廠區工作時相互合作的效率和服務質量的指標。相應管理人員可以針對實際情況（例如根據實際的利潤和損失等）對某些監理員之間的默契關系進行量化，對默契程度特別佳的給定一個正值，對默契程度尤為不好的給定一個負值，而對其他默契程度不突出的設為0。在極端的情況，監理員兩兩之間默契程度都不為0，這時候監理員之間默契程度用一個n×n的矩陣R表示；對于一般情況，表示造船監理員間默契程度的R是一個稀疏矩陣。從而對于任意調度方案，都可以對每個廠區計算分配到該廠區監理員之間默契程度的總和，再匯總求和計算出該調度方案下默契總值p。

造船監理員對工作地點（即廠區）的偏好是指允許監理員根據自己的身體狀況、家庭狀況、作息習慣和風俗習慣等多方面因素，自行確定對工作地點（廠區）的偏好，以供制作調度方案時參考。監理員對于廠區的偏好程度也分為正值、0和負值。表示監理員對廠區的偏好程度的是一個n×m的矩陣，用L來表示。

監理員之間默契程度和他們對工作地點的偏好程度這兩個約束屬于軟性約束，考慮上述約束將有助于提高他們工作的積極性和質量。為了不降低獲得可行解的機會，它們將被轉化到目標函數中：用目標函數式（6）替代式（5）。于是得到一個擴展的造船監理員調度問題模型。

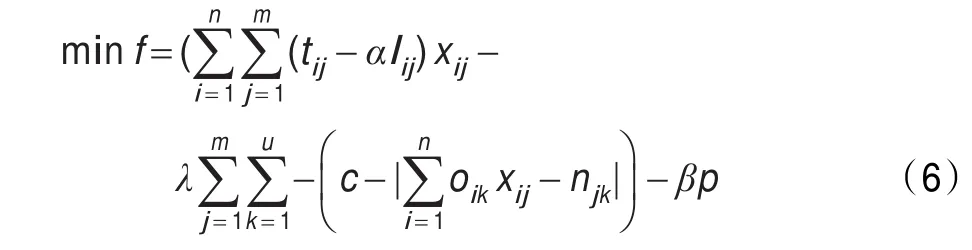
其中lij表示第i名監理員對第j個廠區的偏好程度；α和β分別為造船監理員對工作地點偏好和造船監理員間默契程度的權重系數，其值由相應管理人員根據實際情況賦值。

4 基于模擬退火遺傳算法的問題求解

4.1 模擬退火遺傳算法

遺傳算法（Genetic Algorithms）是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型，是一種通過模擬自然進化過程搜索最優解的方法[11-12]。遺傳算法廣泛應用于傳統搜索方法難以解決的高度復雜的非線性領域，且在組合優化方面展示了良好的優越性。因此，將遺傳算法應用于本文研究的問題是可行的。

雖然遺傳算法是一種通用的全局優化算法，但是遺傳算法局部搜索能力卻較差。而遺傳算法中每一代群體的優良度直接影響后代的優良度與整個算法的效率。大量的研究表明遺傳算法性能可以通過結合局部搜索步驟進行改善。這樣的算法通常被稱作“混合算法”[11]。模擬退火算法（Simulated Annealing）是基于Monte Carlo迭代求解策略的一種隨機尋優算法，其出發點是基于固體物理退火過程與組合優化之間的相識性，模擬退火算法由某一較高溫度開始，利用具有概率突跳特性的Metropolis抽樣策略在解空間中進行隨機搜索，伴隨溫度不斷下降重復抽樣過程。固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最后在常溫時達到基態，內能減為最小，模擬退火算法是一種局部搜索能力很強的算法[13]。將模擬退火的思想引入遺傳算法，對交叉和變異后的個體實施Boltzmann接受策略，不但增強了遺傳算法的全局收斂性，并且使遺傳算法在進化后期有較強的爬山性能，加快了進化后期的收斂速度，形成模擬退火遺傳算法，可以有效緩解遺傳算法的壓力[14-15]。針對本文研究的問題，將遺傳算法與模擬退火算法結合起來，使用模擬退火遺傳算法，以提升遺傳算法局部搜索能力，從而對性能進行改善。

4.2 基于模擬退火遺傳算法的問題求解流程

本文采用實值編碼方式，個體長度為待調度的造船監理員人數，其中個體中每個元素的值表示該監理員被派往的廠區。這樣的編碼方式可以自動滿足約束式（2）。

本文研究的問題一個主要方面是差旅費開銷。根據實際情況，在一次調度前可以知道上一個調度周期所有待調度監理員所處的廠區和此次調度周期廠區對監理員相應需求情況。根據這些數據，用計算機可以快速計算出哪些廠區對哪些專業監理員需求人數超出已有人數（即本次調度前已在此廠區的相關監理員人數），而這些廠區的相應監理員是無需調度到其他廠區的。這樣在不考慮軟性約束時事先確定哪些造船監理員不必要調度到其他廠區，從而能生成讓這些監理員原地待命的初始群體。同時為保證初始群體的多樣性，隨機生成其他監理員所派往的廠區編號。并且為更好地考慮到軟性約束，隨機選取任意“原地待命”的監理員，隨機生成他們所派往的廠區。這樣啟發式生成初始種群的優勢是能生成性能較好的個體，提高算法的進化速率。雖然啟發式生成初始種群可能會增大運行開銷，但是實驗表明，這部分開銷在研究的問題整體規模中是極小的且可接受的。

一般來說，遺傳算法中適應度計算最費時間，而且需要不斷產生新一代，每一代又有若干個體，提高遺傳算法的運行速度顯得尤為重要。由于遺傳算法的內在并行機制，并行處理將有效地改善遺傳算法的性能。遷移（migration）是并行遺傳算法引入一個新的算子并在進化過程中使子群體互相交換個體的過程[14]。本文將使用遷移策略將子群體中最好的個體發給其他的子群體，通過遷移可以加快較好個體在群體中的傳播。算法流程如下：

步驟1輸入監理員數量n、廠區個數m；輸入差旅費矩陣T、專業矩陣O，人際關系矩陣R及地點偏好矩陣L內元素的值。

步驟2啟發式方法生成初始群體；輸入遺傳算法配置參數；設定初始溫度tmax終止溫度tmin，溫度下降率ν，t=tmax以及局部搜索參數w等運行參數。

步驟3采用遺傳算法對種群進行交叉、變異、非線性排序和選擇。

步驟4對于種群中的每個個體調用模擬退火算法。

步驟5更新溫度if(t＞tmin)thent=t*ν；否則算法結束，輸出調度結果。

步驟6轉到步驟3。

5 實驗結果及分析

仿真環境的運行平臺為Matlab，在Core i5 2.3 GHz的CPU和4 GB RAM的PC上運行。為了方便說明和驗證，選用一組規模較小并且典型的數據進行測試。假設共有15名造船監理員，掌握5個不同的專業，其中一位監理員同時掌握兩個專業；共有5個廠區。設定在調度前15名監理員平均分配到5個廠區。根據現實中機票價格，設定表示15名監理員的差旅費矩陣T為：

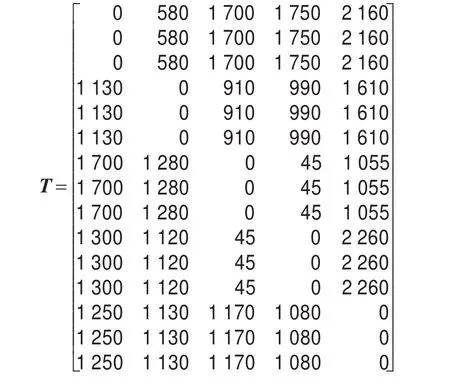
表示監理員之間默契程度的矩陣R為15×15的矩陣，令r1，15=-1，其他元素都為0；表示15名監理員地點偏好的矩陣L為15×5的矩陣，其中l10，4=l11，4=1，l12，1=-1，其他元素值為0；表示監理員掌握專業的矩陣O為：

本文使用的算法運行參數如表2和表3。

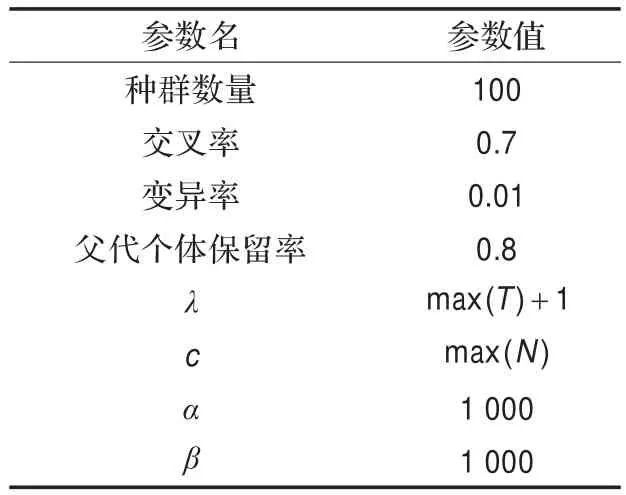
表2 求解過程中基本遺傳算法使用的參數

表3 求解過程中有關子種群和遷移使用的參數

從算法描述中可以看出，算法外循環執行次數與tmax，tmin和ν有直接聯系。一般來說，tmax要取得足夠大，使得能夠接受劣解的概率比較大，在初始時能幾乎100%的概率接受劣解。但由于本次實驗數據規模較小，經過多次實驗，最后采用的有關模擬退火參數如表4。

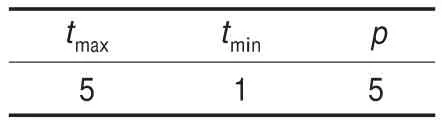
表4 求解過程中有關模擬退火相關參數

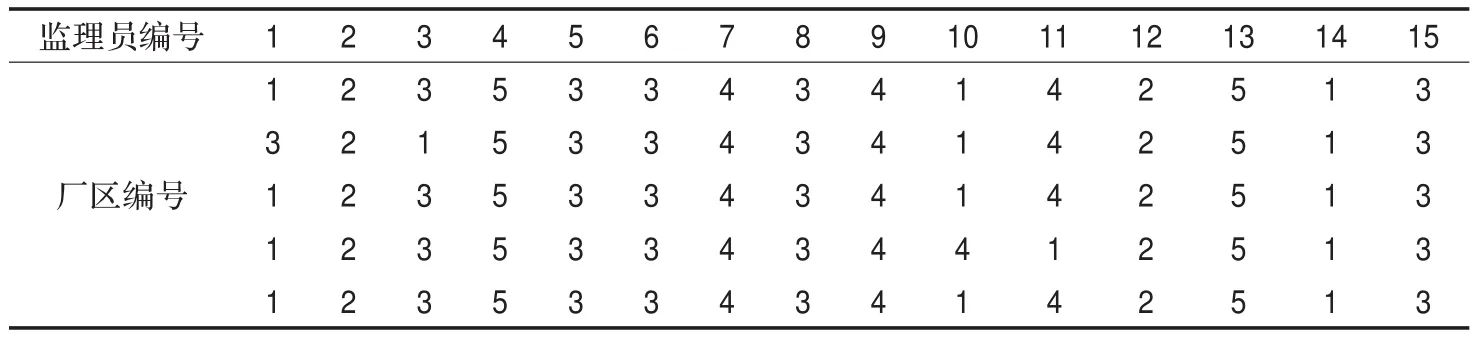
表5 仿真實驗調度結果

從以上的參數和實驗數據描述可以看出，第14名監理員同時掌握第4和第5號專業；而所有廠區對第5號專業監理員的需求是2，對第3和第4號專業的需求為4，對其他專業需求人數都為3；第1號表示不愿與第15號監理員共事；第10號監理員和第11號監理員更偏好第4號廠區，而第12號監理員不愿去第1號廠區。在接下來的仿真實驗中將著重考察這些要求是否滿足。

運行20次，平均耗時為3.57 s。圖1給出了隨機某次實驗過程中最優解的變化，可以看出在較少的迭代次數內就可以獲得較理想最優解。注意圖中最優解的值只是本模型和算法得出的用于量化的值，并非真實費用開銷。

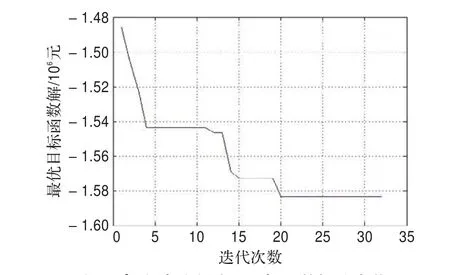
圖1 實驗過程中最優目標函數解的變化

隨機選取5次運行結果，實驗結果（即調度結果）如表5所示。

從以上實驗結果可以看出，對于硬性約束要求，調度結果都很好滿足了廠區對各專業監理員人數的需求且沒有出現“應留守卻被調離”等這樣的無意義調度；同時總差旅費是最少的，例如對于第6號監理員，如若人工調度可能憑感覺做出將第6號監理員繼續留在第2號廠區的決定，但仿真實驗結果表明，第6號監理員調度至第3號廠區并將第2號和第9號監理員分別調度至第2號和第4號廠區更加節省調度開銷。除表5中第二個調度結果對第1號監理員與第15號監理員默契程度沒有考慮周到外，其余調度結果都較好滿足了有關人性化的軟性約束要求，體現了調度人性化，如第10號至第12號監理員對特定廠區的偏好等要求都被充分滿足。最優實驗解和最差實驗結果相比偏差約為0.635%，算法有較好的穩定性。

為驗證系統的實用性，繼續根據某監理公司實際情況進行仿真實驗，每次調度的監理員人數達到百人。實驗參數和變量因問題規模的增大而相應變大。實驗取得理想結果。

6 結束語

本文是對我國造船監理公司監理人員調度問題的一個初步研究，旨在探討一種系統解決針對實際造船監理公司監理人員調度問題的思路與方法。根據我國船舶建造監理的實際情況，歸納出一系列硬性約束和軟性約束，并建立了一個較通用的造船監理人員調度的數學模型。同時所建立模型有較好的可塑性和可擴展性，不同的船舶建造監理公司可以依據實際情況將自身的獨特要求以軟硬約束的形式融入模型中。

在數學模型的基礎上，宏觀采用遺傳算法對該問題求解，通過啟發式生成種群和引入遷移策略改進算法效率，并引入模擬退火算法改進遺傳算法的局部搜索能力。仿真實驗驗證了模型有效且算法有較好的執行效率和魯棒性，具有一定的實用價值和經濟效益。在未來的研究中，將進一步改善模型和算法。

[1]張瑩.淺談船舶監造的管理方法[J].中國水運，2010，10（8）：10-11.

[2]李海平.船舶建造工程的監理工作[J].中國水運：學術版，2010，6（2）：42-44.

[3]Sabar M，Montreuil B，Frayret J M.A multi-agent-based approach for personnel scheduling in assembly centers[J]. Engineering Applications of Artificial Intelligence，2009，22（7）：1080-1088.

[4]Sabar M，Montreuil B，Frayret J M.An agent-based algorithm for personnel shift-scheduling and rescheduling in flexible assembly lines[J].Journal of Intelligent Manufacturing，2012，23（6）：2623-2634.

[5]Kabak O，Ulengin F，Aktas E，et al.Efficient shift scheduling in the retail sector through two-stage optimization[J]. European Journal of Operational Research，2008，184（1）：76-90.

[6]Bai Ruibin，Burke E K，Kendall G，et al.A hybrid evolutionary approach to the nurse rostering problem[J].IEEE Transactions on Evolutionary Computation，2010，14（4）：580-590.

[7]Lu Zhipeng，Hao Jinkao.Adaptive neighborhood search for nurse rostering[J].European Journal of Operational Research，2012，218（3）：865-876.

[8]任守綱，徐煥良，李相全.基于遺傳算法的軟件項目人力資源調度研究[J].計算機應用研究，2008，25（12）：3563-3567.

[9]沈吟東，陳名暉，鄧婕.利用矩陣向量化變換求解護士排班問題[C]//中國控制與決策會議論文集，2008：1019-1022.

[10]沈吟東，蘇光輝.帶約束的護士排班模型和基于變換規則的優化算法[J].計算機工程與科學，2010，32（7）：99-103.

[11]Krasnogor N，Smith J E.A tutorial for competent mimetic algorithms：model，taxonomy and design issues[J].IEEE Trans on Evol Comput，2005，9（5）：474-488.

[12]葛繼科，邱玉輝，吳春明，等.遺傳算法研究綜述[J].計算機應用研究，2008，25（10）：2911-2916.

[13]曹云健，董晶.基于模擬退火遺傳算法的服務選擇[J].計算機工程與設計，2011，32（10）：3507-3510.

[14]Potts J C.The development and evaluation of an improved genetic algorithm based on migration and artificial selection[J].IEEE Trans on SMC，1994，24（1）：73-86.

[15]王銀年，葛洪偉.求解TSP問題的改進模擬退火遺傳算法[J].計算機工程與應用，2010，46（5）：44-47.

FU Hao,GE Hongwei,SHAO Changlu,ZHU Liang

School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China

Quickly and effectively scheduling members of shipbuilding supervision of different majors to specific shipyards improves the efficiency of shipbuilding and ensures the constructional quality.Because lack of general models and effective scheduling means for above-mentioned issue in China,this paper establishes mathematical models with a series of hard constraints and soft constraints to solve this problem.Followed by the models,a hybrid genetic algorithm based on simulated-annealing genetic algorithm is applied to solving this problem.Simulated experiments verify that the model and the algorithm are feasible and effective.

scheduling shipbuilding inspectors;construction of ships;personnel scheduling;hybrid genetic algorithm;NPproblem

A

TP302.1

10.3778/j.issn.1002-8331.1212-0055

FU Hao,GE Hongwei,SHAO Changlu,et al.Models and hybrid genetic algorithm for scheduling shipbuilding inspectors.Computer Engineering and Applications,2014,50（21）：238-242.

符昊（1991—），男，本科，主要研究方向為人工智能；葛洪偉（1967—），男，博士，教授/博士生導師，主要研究方向為模式識別、人工智能和算法分析；邵長魯（1988—），男，碩士研究生，主要研究方向為系統開發、資源調度；朱亮（1991—），男，本科。E-mail：haofu@ucdavis.edu

2012-12-05

2013-03-19

1002-8331（2014）21-0238-05

CNKI出版日期：2013-03-29，http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1540.014.html