汽車發(fā)動機氣門彈簧的最優(yōu)化設計與計算

寇桂岳，甘志梅，孫 林，謝素鑫

(1.南昌工程學院機械與電氣工程學院，330099，南昌；2.江西省科學院生物資源研究所，330096，南昌；3.江西工業(yè)職業(yè)技術學院，330039，南昌)

汽車發(fā)動機氣門彈簧的最優(yōu)化設計與計算

寇桂岳1，甘志梅1，孫 林2*，謝素鑫3

(1.南昌工程學院機械與電氣工程學院，330099，南昌；2.江西省科學院生物資源研究所，330096，南昌；3.江西工業(yè)職業(yè)技術學院，330039，南昌)

闡述了汽車發(fā)動機氣門彈簧的作用，分析其最優(yōu)化設計的設計變量、目標函數和約束條件，提出了氣門彈簧最優(yōu)化設計的數學模型，并通過實例進行驗證說明，該模型可提高氣門彈簧的設計效率。

氣門彈簧；約束函數；最優(yōu)化設計；數學模型

0 引言

配氣機構是汽車發(fā)動機最重要的組成部分之一，而氣門彈簧是配氣機構氣門組的重要零件，其功用是保證氣門關閉時能緊密地與氣門座或氣門座圈貼合，并克服在氣門開啟時配氣機構產生的慣性力，使傳動件始終受凸輪控制而不相互脫離[1-4]。因此，氣門彈簧應具有合適的剛度、足夠的抗疲勞強度、質量要輕、彈力要小以及避免在工作時發(fā)生顫振現(xiàn)象[1-2]。本文對氣門彈簧設計的變量、目標函數及約束條件進行了分析，提出了氣門彈簧優(yōu)化設計的數學模型，并進行實例驗證數學模型的可行性，旨在克服傳統(tǒng)設計方法耗費大量人力物力的缺陷，降低制造成本，提高產品的市場核心竟爭力。

1 氣門彈簧最優(yōu)化設計數學原理

1.1最優(yōu)化參數的確定

圓柱形螺旋氣門彈簧設計時，除選材料及規(guī)定熱處理要求外，主要是根據最大工作載荷、最大變形以及結構要求等來確定彈簧的鋼絲直徑d、中徑D2、工作圈數n、節(jié)距t或螺旋升角α和高度H等。通常取彈簧鋼絲直徑d，彈簧中徑D2和彈簧工作圈數n為最優(yōu)化設計的設計變量，即：

(1)

1.2建立最優(yōu)目標函數

目標函數可根據彈簧的工作特點和對它的專門要求來建立。例如，對于因工作特點極易導致疲勞損壞的彈簧，則應以疲勞安全系數最大作為最優(yōu)化設計的目標；對于安裝空間很緊、要求盡量減小輪廓尺寸的彈簧，則應以其外徑或高度最小，從而得到最小安裝尺寸作為最優(yōu)化設計的目標，本文以彈簧彈力最小作為最優(yōu)化設計的目標，這時目標函數可表達為

(2)

1.3約束函數的確定

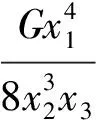
(3)

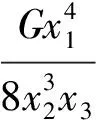
(4)

式中G為彈簧材料的剪切彈性模量。

1.3.2 彈簧強度約束函數的確定 根據彈簧的強度條件：

式中：τmax為在最大工作載荷;K為曲度系數;[τ]為許用扭轉應力。

由此得約束條件：

(5)

1.3.3 彈簧疲勞強度約束函數的確定 當彈簧承受交變載荷并在Fmax及Fmin之間作交替變化時，在鋼絲截面內側所產生的相應扭轉應力分別為：

對于τmin為常數的彈簧，其疲勞強度安全系數為

式中：[S]為許用安全系數;τ0為彈簧材料的脈動疲勞極限。

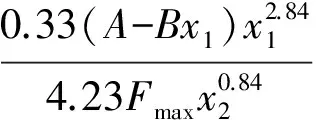
(6)

1.3.4 彈簧穩(wěn)定性約束函數的確定 根據壓縮彈簧的穩(wěn)定條件：

得約束條件

(7)

式中bC為臨界高徑比。

1.3.5 簧絲直徑約束函數的確定 根據彈簧鋼絲的產品尺寸規(guī)格，給出彈簧鋼絲直徑d的限范圍：dmin≤d≤dmax，從而得約束條件

g6(X)=dmin-x1≤0

(8)

g7(X)=x1-dmax≤0

(9)

1.3.6 彈簧中徑約束函數的確定 根據安裝空間對其中徑D2的限制而有

g8(X)=D2min-x2≤0

(10)

g9(X)=x2-D2max≤0

(11)

1.3.7 彈簧工作圈數約束函數的確定 根據對工作圈數n的規(guī)定范圍nmin≤n≤nmax而有

g10(X)=nmin-x3≤0

(12)

g11(X)=x3-nmax≤0

(13)

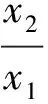
(14)

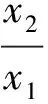
(15)

1.4最優(yōu)化設計數學模型的確定

由上述得到的最優(yōu)化條件和約束條件，其數學模型可以歸結為：

2 氣門彈簧實例設計計算

設對江鈴某一小型柴油發(fā)動機氣門彈簧進行優(yōu)化，其不同工況的轉速為：怠速850 r/min；中速時2 500 r/min；高速(額定轉速)時3 600 r/min,其氣門彈簧材料采用65Mn，剪切彈簧性模量G=81 340 MPa，最大變形量λ=31.17 mm，工作溫度T=126 °C，彈簧結構：2.5 mm≤d≤6 mm，30 mm≤D≤60 mm，彈簧的工作圈數3≤n1≤6，彈簧支承圈數n2=2.5，彈簧的旋繞比C=(D/d)≥6。

對于單目標多約束的優(yōu)化設計的計算方法很多，本文以彈力最小為目標，采用遺傳算法進行優(yōu)化設計計算。

遺傳算法中的4個參數需預先確定M群體大小，既群體中含個體的數目，通常情況下取20～100，如果問題帶有約束，M應取的大一些，以確保群體具有足夠數目的可行解，文中取M=500。氣門彈簧的原始值，即：

X0=[4 43 4.5]T通過計算彈簧彈力為226.5 N。

使用Turbo-C編制的程序進行計算，遺傳算法的計算結果為：

X*=[3.8 39.5 5]T通過計算彈簧彈力減少為200.5 N，而且質量有所減少。

3 結論

通過分析與計算可以看出，采用遺傳算法對氣門彈簧進行最優(yōu)化設計，在保證氣門彈簧工作性能要求的同時減小了彈簧的彈簧力，如果全車都使用這種優(yōu)化后的彈簧則整臺發(fā)動機在配氣機構上消耗的功率會減少，進而間接地提高了發(fā)動機的輸出功率。與傳統(tǒng)的彈簧設計方法相比，提高了發(fā)動機的燃油經濟效益，從而大大提高了市場竟爭力。

[1]劉惟信.機械最優(yōu)化設計(第二版)[M].北京:清華大學出版社,1994.

[2]陳家瑞.汽車構造(第五版)[M].北京:人民交通出版社,2006.

[3]濮良貴,紀名剛.機械設計(第七版)[M].北京:高等教育出版社,2001.

[4]《鋼鐵材料手冊》總編輯委員會.鋼鐵材料手冊(第8卷),彈簧鋼[M].北京:中標準出版社,2003.

OptimizationDesignandCalculationoftheAutomotiveEngineValveSpring

KOU Guiyue1,GAN Zhimei1,SUN Lin2*,XIE Suxin3

(1.Nanchang Institute of Technology,330099,Nanchang,PRC;2.Biological Resources Institute,Jiangxi Academy of Sciences,330029,Nanchang,PRC;2.Jiangxi Industry Polytechnic College,330039,Nanchang,PRC)

This paper analyzes the automotive engine valve springs role.Analyze the design variables of the optimal design,objective function and constraints.A mathematical model of optimize design of engine valve spring was advanced in the paper but verified by the example shows.This approach improves the efficiency of valve spring design.

valve spring;restraint function;optimize design;mathematical model

2014-05-19;

2014-06-23

寇桂岳(1981-)，男，碩士，講師，主要從事發(fā)動機動力學研究。

南昌工程學院青年基金項目(2014KJ015)；江西省科學院產學研合作資金項目(2013-09)。

*通訊作者：孫 林(1962-)，男，副研究員，主要從事汽車橡膠生產及工藝方面的研究。

10.13990/j.issn1001-3679.2014.04.008

TH164

A

1001-3679(2014)04-0459-03