近壁面水下爆炸氣泡運動的數值計算研究

李 健，林賢坤，榮吉利，項大林

(1. 廣西科技大學 汽車與交通學院，廣西 柳州 545006； 2. 北京理工大學 宇航學院，北京 100081)

當氣泡在結構表面附近脈動時，在膨脹階段被結構表面輕微地排斥開，而在坍塌階段被結構強烈地吸引，并產生高速射流。射流的成因可以用著名的Bjerknes效應來解釋。一般情況下，由于Bjerknes力作用，氣泡會被水中結構吸引而向結構方向運動，在浮力、慣性力等因素的影響下，沿著氣泡坍塌方向會形成高速射流，且射流會穿透氣泡并沖擊氣泡壁的另一面，最終作用于結構造成結構的破壞。由于氣泡脈動、坍塌、射流形成等一系列物理現象非常復雜，難以通過理論方法得出氣泡運動過程的解析解，因此，氣泡與結構相互作用主要是通過采用實驗或仿真的方法進行研究。

實驗方法主要是利用小藥量炸藥爆炸[1-2]或借助氣泡發生器在水中形成氣泡[3-4]，并將結構置于氣泡附近，以此研究近壁面氣泡的運動特性。數值仿真計算方面目前大都采用邊界積分法[5-8]或基于有限體積法的非線性仿真軟件[9-11]。邊界元方法只在邊界離散，大大降低了計算成本，但是在射流產生、氣泡破碎及環形氣泡形成方面有一定的局限性。有限體積法或流體體積法可以較好的模擬流體流動過程中的間斷問題，其缺點是需要對每個空間位置進行網格離散，導致計算量大且介質間的交界面難以精確追蹤、捕捉。

由于氣泡與結構之間相互作用的現象非常復雜，目前仍有許多現象沒被揭示，關于射流特征、環形氣泡形成等方面的研究文獻甚少，而基于有限體積法結合界面追蹤、捕捉方法進行氣泡特性的研究更是十分罕見。為此，為了對結構附近氣泡運動數值模擬研究提供有益的補充，本文從氣泡與剛性壁面相互作用的基本現象入手，系統地研究剛性壁面附近氣泡的動力學特性，包括剛性壁面角度、氣泡與壁面距離等參數對氣泡運動和射流方向、速度的影響，旨在為相關研究提供參考。

1 理論背景

1.1 氣泡運動初始條件

要模擬氣泡的運動，需要先求出氣泡的初始半徑。目前關于氣泡初始狀態求解的方法較多，主要包括Rayleigh模型[12]和Frost和Harper[13-14]提出的氣泡體積加速度模型，后者主要是分別建立了藥包參數和流場壓力以及氣泡體積加速度與流場壓力之間的關系，并利用壓力等效關系最終確定氣泡的初始半徑與初始膨脹速度。此方法已經能夠較準確地描述氣泡的初始條件，但是考慮到從炸藥點火到氣泡脈動是一個連續的物理過程，為了更為準確的模擬整個水下爆炸過程，本文將基于MSC.DYTRAN軟件，先采用一維模型模擬炸藥的整個爆轟過程，通過將一維計算結果映射到三維流場中，用以確定三維氣泡脈動的初始條件，以此實現炸藥從爆轟到氣泡脈動全過程進行數值計算，為水下爆炸數值計算提供一種新的解決方案。

為驗證一維數值計算的正確性，將爆炸過程中流場不同距離沖擊波壓力峰值與經驗公式進行對比。圖1為裝藥量為55 g的TNT炸藥在水下爆炸不同測點距離處沖擊波的波形曲線，其中炸藥采用JWL狀態方程描述，各參數的選擇可參見文獻[1]。從圖中可以看到，隨著距離的增加，沖擊波壓力峰值衰減較快，而沖擊波波形與真實情況相吻合，表現為波峰“尖銳”且后續無明顯的尾隨振蕩。

圖1 不同測點距離時沖擊波波形曲線

表1為不同工況下沖擊波壓力峰值與經驗公式的對比，通過對比可以看到，數值計算結果與經驗公式具有較好的一致性，誤差能夠控制在7%以內，驗證了數值計算的正確性。

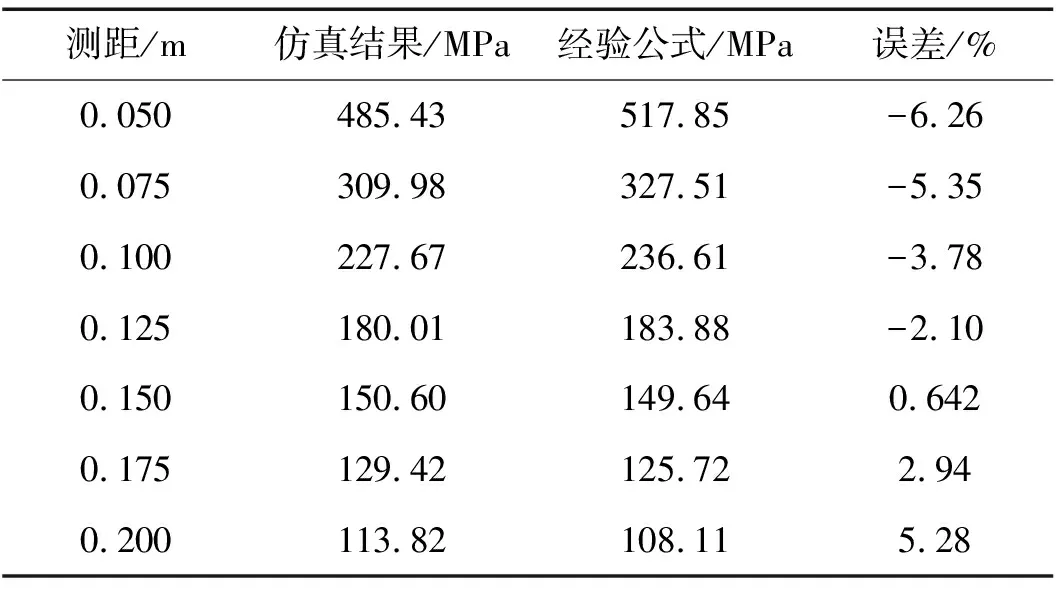
表1 不同測點沖擊波壓力峰值仿真結果與經驗公式的對比

1.2 氣泡狀態方程

由于氣泡脈動過程中其內部壓力遠低于炸藥爆轟過程中的壓力，因此不太適宜采用JWL狀態方程描述氣泡，一般情況下，氣泡脈動過程中，認為氣體的壓力僅和氣泡的初始狀態及體積有關[14]，即氣泡內的壓力P與氣泡體積V的關系可以表示為：

(1)

(2)

其中：Pc為可冷凝氣體的飽和蒸汽壓，量級與大氣壓相當，一般可忽略；P0和V0分別為氣泡形成時的初始壓力和初始體積，W為裝藥量，γ為氣體的比熱比，對于TNT水中爆炸的爆轟產物而言，γ取1.25。

1.3 流場初始條件定義

在利用一維有限元模型完成了炸藥爆轟與沖擊波傳播過程的數值計算后，可以獲得氣泡壁運動速度、氣泡內壓力等參數，若要進行三維氣泡的數值模擬，還需要定義流場的初始條件(如靜水壓)與邊界條件。為此，根據初值及邊界條件特點，利用定義初始條件和邊界條件的子程序接口EXINIT及EXFLOW2，開發了定義流場初值和邊界條件的子程序，其思路就是根據模型中各單元節點的實際位置，將與之相對應的靜水壓力通過EXINIT和EXFLOW2子程序逐一賦到整個流場的單元節點上。

2 結果與討論

2.1 模型驗證

為驗證三維氣泡運動數值計算的正確性，將裝藥量為55 g的球形炸藥置于水下3.5 m處，并將氣泡脈動體積時程曲線與文獻[1]中的實驗進行對比，對比結果如圖2所示。從圖中可以看出，本文所采用的由一維向三維映射方法所計算的氣泡體積與脈動周期較文獻[1]中所采用的仿真方法與實驗測試結果更為接近，驗證了數值計算模型、流場初始條件與邊界條件子程序開發、狀態方程選取的正確性。

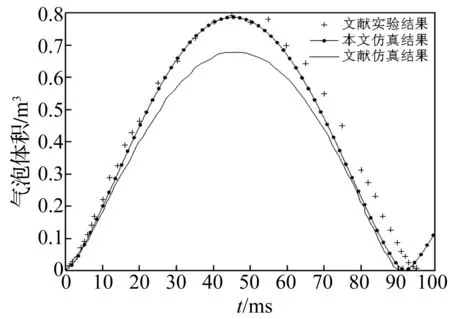
圖2 氣泡脈動半徑時間歷程曲線

為驗證本文所建立數值計算模型在模擬剛性壁面附近三維氣泡運動的有效性，根據文獻[1]中的實驗工況，即將55 g炸藥置于水下3.5 m處，并在其水平距離0.4 m處垂直放置一剛性平板，通過高速相機捕捉各時刻氣泡運動特性(實驗結果如圖3所示)。

根據實驗測試工況，采用流-固耦合方法定義流體與結構的相互作用，建立近剛性壁面三維氣泡運動模型，氣泡與壁面相互作用過程的計算結果如圖4所示。通過對比圖3與圖4發現，氣泡在各時刻的運動均具有比較好的一致性，特別是在t=96 ms時，可以通過仿真結果清晰地看到氣泡坍塌會發生于遠離結構一側，形成由右下指向左上的射流，射流最終擊穿氣泡而作用在結構上。

圖3 55 g炸藥在水下3.5 m距垂直剛性面40 cm處爆炸氣泡運動實驗結果

圖4 55 g炸藥在水下3.5 m距垂直剛性面40 cm處爆炸氣泡運動仿真結果

2.2 特征參數對氣泡運動的影響

為研究剛性壁面附件氣泡的運動規律，本節將以氣泡與垂直放置剛性壁面相互作用數值計算模型為基礎，研究氣泡與剛性壁面角度、距離等參數對氣泡運動特性的影響規律。由于氣泡坍塌、射流方向、射流速度等物理現象的產生與爆心初始位置、氣泡脈動周期、氣泡最大半徑等關鍵參數有密切關系，因此以氣泡的最大半徑Rm為特征長度，中點處靜水壓力pamb為特征壓力，則特征時間為t=Rm(ρ/pamb)0.5，氣泡與剛性壁面垂直距離為d=L/Rm，速度的無量綱表達式為v/(Rm/t)，以此研究初始距離與角度對氣泡運動特性的影響規律。

3.2.1 剛性面角度對氣泡的影響

本節首先研究氣泡與剛性壁面距離與角度變化時對氣泡射流角度與射流速度的影響。圖5為在氣泡與剛性壁面初始距離為Rm且剛性壁面與水平面的夾角分別為0°、45°、90°、135°和180°時氣泡膨脹過程。從圖5可以看出，在Bjerknes力作用下，氣泡在膨脹時會被剛性壁面吸引，且氣泡最大半徑不會隨著剛性壁面角度的變化而變化，表現為不同工況下氣泡脈動最大半徑及膨脹到最大半徑所用的時間基本相同。

圖6為與圖5各工況相對應的氣泡收縮過程。從圖中可以看出，當氣泡與剛性壁面初始距離較近時(特征距離為Rm)，氣泡受剛性壁面的影響較大，表現為氣泡坍塌發生于遠離結構一側，且最終的射流方向基本垂直于剛性壁面，從射流最終擊穿氣泡的時間來看，射流發生于氣泡收縮至最小體積并開始第二次膨脹階段。此外，當剛性壁面與水平面夾角大于90°時(如圖6(d)、(e)所示)，由于此時Bjerknes力沿豎直方向投影與浮力方向相反，會對氣泡坍塌與射流的形成有影響，導致射流速度降低，表現為射流擊穿氣泡所需時間較其它工況要長。

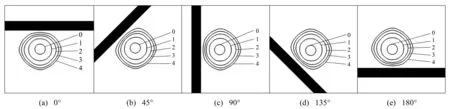
無量綱時間: (0)0.00, (1)0.21, (2)0.42, (3)0.62, (4)1.09

圖7為特征距離為Rm時，氣泡射流方向與壁面法向的夾角的關系曲線。從圖中可以看到，由于特征距離較近，Bjerknes力效果明顯占優，最終氣泡射流基本都是垂直射向結構。當剛性面垂直放置時，氣泡射流與壁面法向夾角值最大，約為4°。

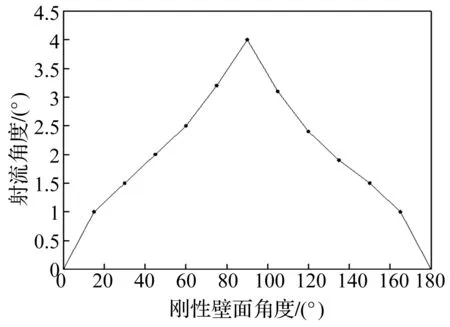
圖7 特征距離為Rm時射流角度與剛性面角度之間的關系

圖8為特征距離為Rm時，氣泡射流速度與剛性面角度的變化關系曲線。從圖中可以看到，隨著剛性面與水平面夾角的增加，氣泡射流速度會逐漸降低，其主要原因就是氣泡坍塌與射流主要受Bjerknes力與浮力的共同作用，Bjerknes力方向主要是氣泡與結構連線方向，而浮力就是沿著豎直方向，當Bjerknes力沿豎直方向分量與浮力作用方向相同時，所形成的合力能使氣泡產生高速射流，而當二者方向相反時，合力導致氣泡射流速度降低。

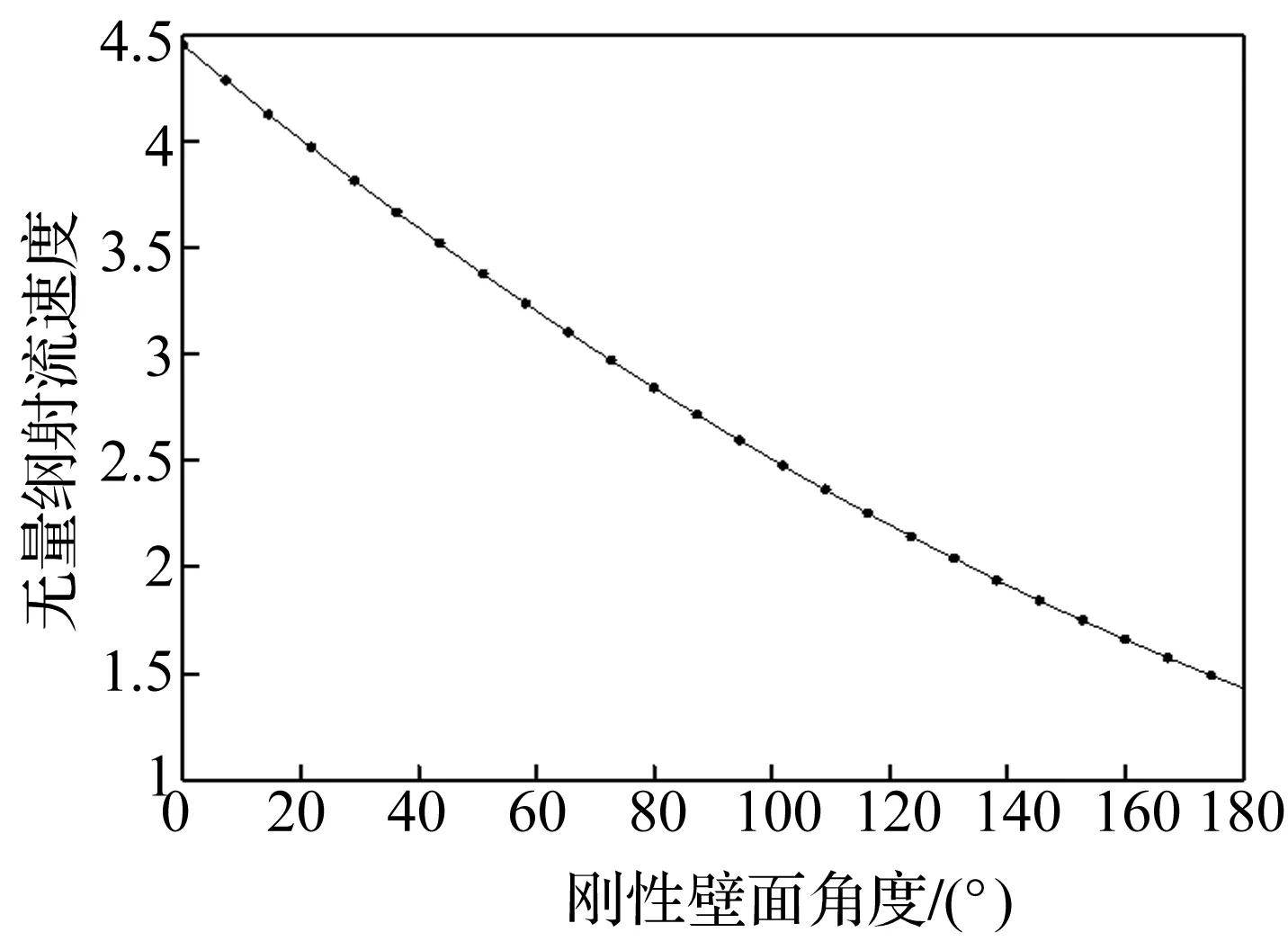
圖8 特征距離為Rm時射流速度與剛性面角度之間的關系

圖9、10分別為特征距離為2Rm時，氣泡射流角度、速度和剛性面放置角度之間的變化關系。從圖9可以看出，射流方向受剛性面角度影響明顯，射流與剛性面夾角會經歷先增加后減小的過程。對比圖7與圖9可以發現，當距離增加時，由于Bjerknes力作用效果減弱，導致氣泡射流方向與結構夾角會有不同程度地增加。從圖10中可以看出，當特征距離不變時，射流速度會隨著剛性面角度的增加而減小，對比圖8與圖10可以發現，當距離增加時，氣泡與結構之間的吸引力減小，導致射流速度降低，且在相同角度情況下，特征距離為Rm所產生的氣泡射流速度約為2Rm時的3倍左右。因此，特征距離對氣泡射流方向與速度影響明顯。

圖9 特征距離為2Rm時射流角度與剛性面角度之間的關系

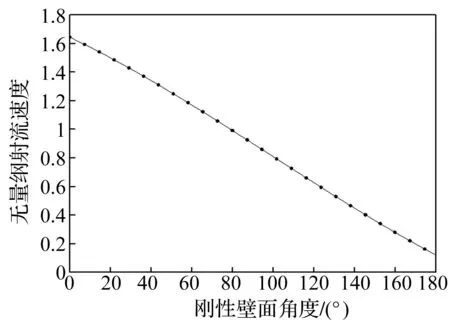
圖10 特征距離為2Rm時射流速度與剛性面角度之間的關系

3.2.2 特征距離對氣泡運動的影響

前述計算結果表明，特征距離對氣泡射流特性影響明顯，且根據圖7所示，當特征距離較小時，氣泡與壁面最大夾角發生在壁面垂直放置時，為此，本節將研究剛性壁面垂直放置時，特征距離對氣泡運動特性的影響。圖11表示氣泡中心與垂直剛性壁面距離分別為2Rm、3Rm和4Rm時氣泡的收縮過程(特征距離為Rm工況參見圖6(c))。從圖中可以看到，當氣泡與剛性壁面較近時，由于Bjerknes力作用效果顯著，氣泡被結構強烈吸引，隨即產生指向結構的射流。當氣泡與結構距離為2Rm時，Bjerknes力作用效果有所減弱，表現為氣泡最終形成的射流方向與剛性面法向夾角增加，而當特征距離大于3Rm時，氣泡無明顯指向結構的射流產生，此時氣泡受結構作用影響較小，基本可以忽略結構對氣泡運動的影響。

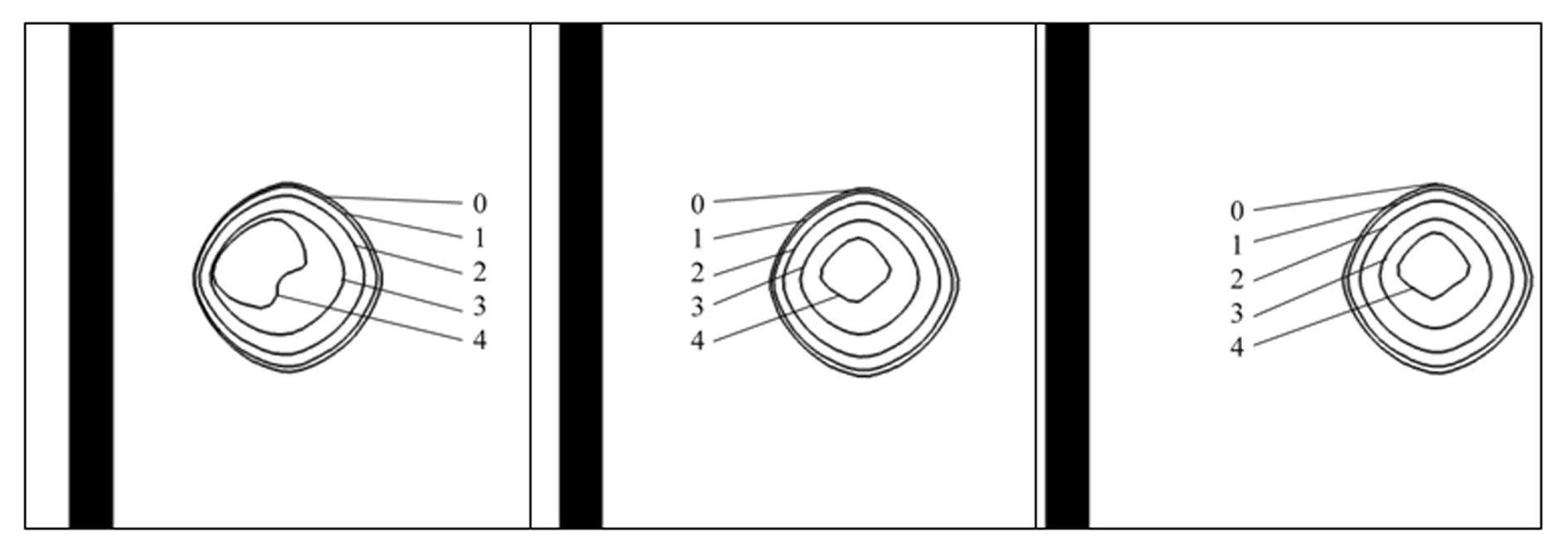
無量綱時間：(0)1.09 (1) 1.33 (2) 1.58 (3) 1.80 (4) 2.03

圖12 氣泡與垂直剛性壁面特征距離與射流角度之間的關系

圖12為氣泡在垂直剛性壁面附近運動，其射流角度與特征距離之間的關系曲線。從圖中可以看到，隨著特征距離的增加，氣泡與剛性面的夾角也隨之增加，特別是當特征距離大于3Rm時，射流角度與垂直剛性面法向的夾角基本為90°，射流方向基本沿著豎直方向，與氣泡在自由場中運動特性類似，表明此時剛性面對氣泡運動影響較小，基本可以忽略。

3 結 論

采用一維有限元模型對爆轟與沖擊波傳播過程進行了仿真分析，以此為基礎，將一維計算結果映射到三維流場中，確定了氣泡脈動的初始條件，并對氣泡與結構相互作用全過程進行了仿真分析，通過與實驗結果的對比，驗證了氣泡初始條件確定方法、子程序開發與模型建立的正確性，以此模型為基礎，通過仿真計算，研究了特征距離與剛性面角度對氣泡運動特性的影響，分析總結相關規律，獲得了如下一些主要結論：

(1) 在一維有限元模型利用JWL狀態方程中模擬炸藥爆轟與沖擊波傳播過程，并將其計算結果作為氣泡脈動的初始條件，在三維仿真模型中采用Tait狀態方程描述氣泡，通過與經驗公式和已有實驗測試結果的對比，驗證了此方法在三維氣泡運動數值模擬的可行性與正確性。

(2) 由于Bjerknes力對氣泡的作用力主要是沿著氣泡與結構的連線方向，而浮力作用是沿著豎直方向，因此，剛性面的角度對氣泡運動、射流方向與射流速度均有不同程度的影響。表現為當二者作用方向相同時，氣泡射流速度較高，反之，氣泡射流速度較低。

(3) 當特征距離在3Rm以內時，由于Bjerknes力作用占優，可以產生指向結構的射流。表現為當初始距離在Rm時，氣泡射流角度與結構法向夾角基本重合，且射流速度較高，射流速度隨著角度的增加而減小；當初始距離在2Rm時，氣泡射流角度與結構法向夾角增加，最大角度出現在剛性面與水平面成120°時，且射流的速度隨著角度的增加而減小。

(4) 隨著特征距離的增加，射流方向與結構法向之間的夾角隨之增加，而射流速度隨著距離的增加而減小。表現為當特征距離在3Rm以外時，射流方向基本與豎直方向重合，即氣泡受結構的影響較弱，基本可以忽略其對氣泡運動的影響。

[1]Klaseboer E, Khoo B C, Hung K C. Dynamics of an oscillating bubble near a floating structure[J]. Journal of Fluids and Structures, 2005, 21:395-412.

[2]李健, 榮吉利. 水下爆炸圓柱殼塑性動態響應實驗及數值計算[J]. 北京理工大學學報, 2008, 28(8): 559-562.

LI Jian, RONG Ji-li. Experimental and numerical investigations of dynamic response for cylindrical shell subjected to underwater explosion[J]. Transactions of Beijing Institute of Technology, 2008, 28(8): 559-562.

[3]張阿漫, 肖巍, 王詩平,等. 不同沙粒底面下氣泡脈動特性實驗研究[J]. 物理學報, 2013, 62(1): 014703, 1-8.

ZHANG A-man, XIAO Wei, WANG Shi-ping, et al. Experimental study of the interactions between a pulsating bubble and sand particles with different diameters[J]. Acta Physica Sinica, 2013, 62(1): 014703, 1-8.

[4]徐玲君, 陳剛, 邵建斌, 等. 不同直徑氣泡在靜水中運動特性的研究[J]. 水動力學研究與進展，2012, 27(5): 582-588.

XU Ling-jun, CHEN Gang, SHAO Jian-bin, et al. Study on motion behavior of bubbles with different diameters in still water[J]. Chinese Journal of Hydrodynamics, 2012, 27(5): 582-588.

[5]Klaseboer E, Manica R, Chan Y C. BEM simulations of potential flow with viscous effects as applied to a rising bubble[J]. Engineering Analysis with Boundary Elements, 2011, 35: 489-494.

[6]張阿漫, 姚熊亮. 水下爆炸氣泡與海底相互作用研究，振動與沖擊, 2008,37(3), 92-98.

ZHANG A-man, YAO Xiong-liang. Interaction between underwater explosion bubble and seabed[J]. Journal of Vibration and Shock, 2008, 37(3), 92-98.

[7]張海鵬, 岳永威, 蘇羅青等. 水下爆炸作用下艦船總縱強度模型實驗方案研究[J]. 振動與沖擊, 2012, 31(6): 175-180.

ZHANG Hai-peng, YUE Yong-wei, SU Luo-qing, et al. Model experimental scheme for longitudinal strength of a warship subjected to underwater explosion[J]. Journal of Vibration and Shock, 2012, 31(6): 175-180.

[8]Cox P E, Blake J R, et al. Bubble interactions near a free surface[J]. Engineering Analysis with Boundary Elements, 2004, 28:295-313.

[9]袁建紅, 朱錫, 張振華. 水下爆炸近距氣泡作用下船體箱型梁損傷特性數值模擬方法研究[J]. 振動與沖擊, 2010, 29(4): 111-116.

YUAN Jian-hong, ZHU Xi, ZHANG Zhen-hua. Numerical simulation method for damage properties of a box-beam with action of underwater near-distance explosion bubble[J]. Journal of Vibration and Shock, 2010, 29(4): 111-116.

[10]李健, 榮吉利, 楊榮杰, 等.水中爆炸沖擊波傳播與氣泡脈動的實驗及數值模擬[J]. 兵工學報, 2008, 29(12): 1437-1443.

LI Jian, RONG Ji-li, YANG Rong-jie, et al. Experiment and numerical simulation of shock wave propagation and bubble impulse of underwater explosion[J]. Acta Armamentarii, 2008, 29(12): 1437-1443.

[11]黃曉明, 朱錫, 牟金磊等. 近距水下爆炸作用下箱形梁模型中垂破壞試驗研究[J]. 振動與沖擊, 2011, 30(2): 20-23.

HUANG Xiao-ming, ZHU Xi,MU Jin-lei, et al. Sagging damage test of box-beam models subjected to close range underwater explosion[J]. Journal of Vibration and Shock, 2011, 30(2): 20-23.

[12]Rayleigh J W. On t he pressure developed in a liquid during the collapse of a spherical cavity [J]. Philos Mag, 1917 , 34: 94-98.

[13]Price R S. Simulitude equations for explosives fired underwater[R]. NSWC: Technical Report NSWC TR, 1979, 80-299.

[14]Hunter K S. Global-shape-function models of an underwater explosion bubble[D]. Faculty of Graduate School of the University of Colorado, Department of Mechanical Engineering, 2001, 16.