板結構-聲場耦合分析的FE-LSPIM/FE-LSPIM法

陳 寧, 于德介, 呂 輝, 夏百戰

(湖南大學 汽車車身先進設計制造國家重點實驗室,長沙 410082)

幾乎所有的聲學問題都與結構-聲場耦合系統有關，因此對結構-聲場耦合系統的研究具有重要的工程意義。結構-聲場耦合系統的分析能為結構件的優化提供重要信息，特別是容易受到聲壓激勵而產生振動的彈性薄壁結構件。板結構-聲場耦合系統包含板結構域、聲場域和兩個域之間的耦合作用。通常，在結構域用位移描述結構的狀態，在聲場域用聲壓描述聲場的狀態[1-2]。

目前，有限元/有限元法(Finite Element Method, FEM)和有限元(FEM)/邊界元法(Boundary Element Method, BEM)是分析結構-聲場耦合系統最常用的數值計算方法。FEM/ BEM與FEM/ FEM相比，能減少模型的單元數量，但其矩陣為非稀疏矩陣，并不一定能提高計算效率；而對于內聲場問題，FEM/ FEM 計算效率往往更高一些；同時兩者的計算結果受模型網格尺寸影響較大，因此FEM/ FEM 和FEM/ BEM 主要用于求解中低頻的結構-聲場耦合 問題[3-4]。Yao等[4]提出的SFEM(Smoothed Finite Element Method)/FEM方法在結構-聲場耦合問題的分析中能取得比FEM/FEM更高的精度。

有限元法雖然得到了廣泛的應用，但仍存在一些不足，如等參單元對于網格幾何變形非常敏感，為了獲得可靠的計算結果，通常需要更精細的網格等。無網格法則有效地避免了有限元的一些缺點，具有精度高、 計算模型不需劃分網格等特點，但無網格法本身存在諸多缺陷，如其形函數不具備克羅內克爾性質，導致不能直接施加邊界條件、計算效率降低等。針對有限元法和無網格技術的特點，Melenk等[5-6]結合有限元和無網格技術，提出了混合有限元-無網格法來分析各類力學問題。其中，單位分解有限元法是一種常用的混合有限元-無網格方法，該方法的基本原理是在不增加支撐點的前提下，通過增加局部支撐函數的階次來構造高階的全局有限元公式。Zhang等[7-8]提出了一種基于單位分解的有限元-最小二乘點插值法(Finite Element-Least Square Point Interpolation Method，FE-LSPIM)，該方法采用的有限元-無網格四邊形單元將有限元形函數和最小二乘點插值形函數相結合，綜合了有限元法和無網格法各自的優點，其形函數具有克羅內克爾性質，具有單元兼容性以及高階完備性，并且成功地應用于靜力學和動力學分析中。隨后姚凌云等[9]將FE-LSPIM推廣到二維聲場的研究之中，并取得了良好的效果。

為了提高結構-聲場耦合分析精度，降低結構-聲場耦合分析中對結構網格尺寸的要求，本文將FE-LSPIM推廣到板結構動力學和三維聲場的分析中，提出用于板結構-聲場耦合問題分析的FE-LSPIM/FE-LSPIM。運用FE-LSPIM/FE-LSPIM分析板結構-聲場耦合問題時，板結構域采用有限元-無網格四邊形單元，聲場域采用有限元-無網格六面體單元。以一個六面體板結構-聲場耦合模型為數值算例進行分析，結果表明，FE-LSPIM/FE-LSPIM繼承了FE-LSPIM適用性好、精度高的特點。與FEM/ FEM和SFEM/ FEM相比，FE-LSPIM/FE-LSPIM的精度更高，對網格尺寸的質量要求更低，能很好地應用于板結構- 聲場耦合分析，具有良好的工程應用前景。

1 基于FE-LSPIM/FE-LSPIM的板結構動力學分析

1.1 板單元的有限元-最小二乘點插值

根據剪切變形理論，如圖1所示，明德林-瑞斯納 (Mindlin-Reissner)板模型的位移分量u,v分別表示為：

u=-wθx(x,y)

v=-wθy(x,y)

(1)

式中:u,v,w分別為板中面x,y,z三個方向的位移，θx和θy分別為xz和yz平面內的轉角。定義彎曲應變為κ，剪切應變為γ，有：

(2)

板結構的橫向剪切剛度本構矩陣Ds和彎曲剛度本構矩陣Db分別可表示為：

(3)

式中，E為彈性模量；t為板單元厚度；ν為柏松比；μ為剪切修正系數[1]。

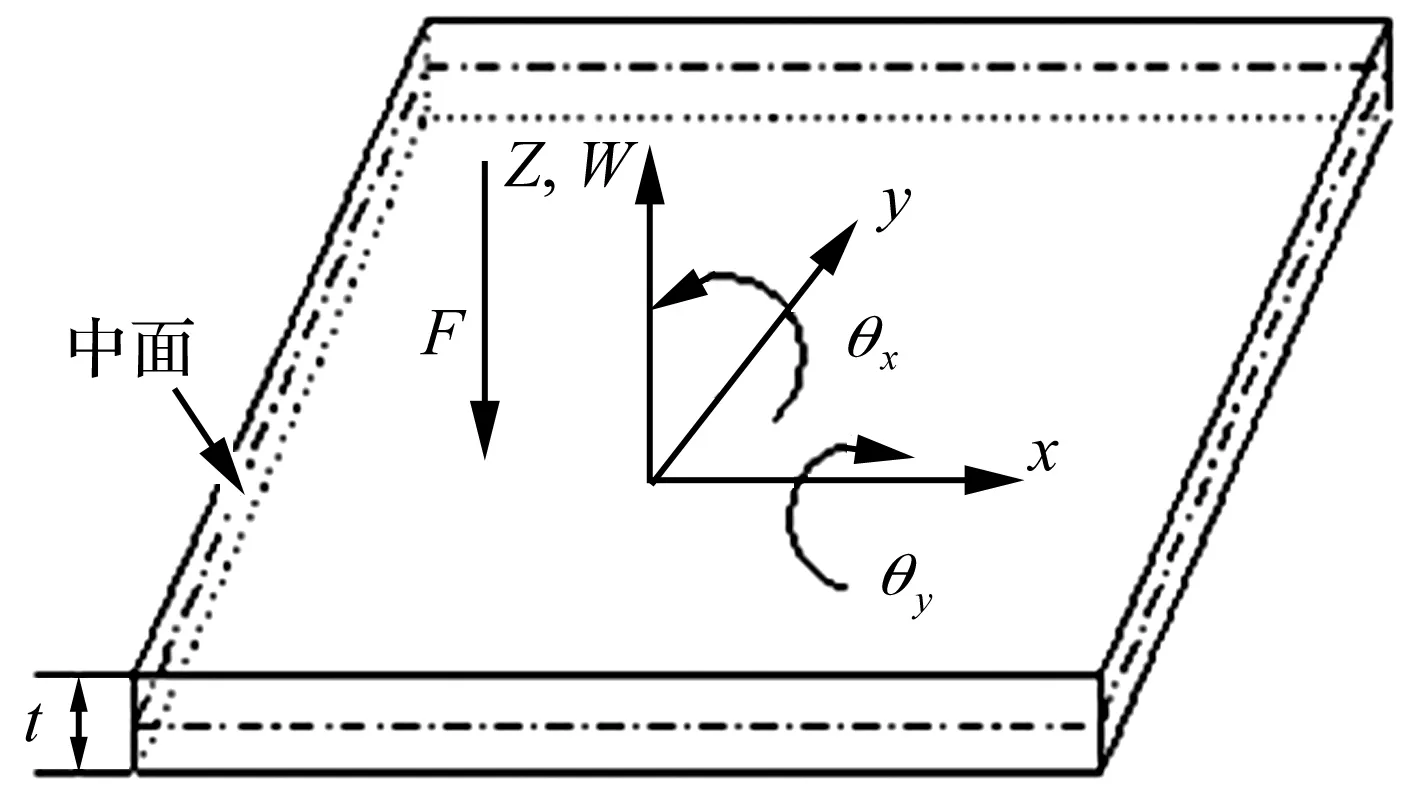
圖1 板單元示意圖

根據標準的有限元法，對板結構域Ω進行離散，四邊形單元數為Ne，節點數為Nd。對于板單元，廣義位移u={θxθyw}T是各自獨立插值的，其表示為：

u(x,y)=Nplateue

(4)

式中:Nplate為四邊形板單元形函數，ue為節點的位移，可以寫成：

(I=1,2,3,4)

(5)

ue={u1(x,y)u2(x,y)u3(x,y)u4(x,y)}T

ui(x,y)={θxiθyiwi}T(i=1,2,3,4)

(6)

節點位移函數ui(x,y)由支撐節點通過LSPIM插值得到。以廣義位移中的撓度對整個求解過程進行推導，撓度w(x,y)可表示為：

w(x,y)=NIwe

(7)

向量we表示對應的四邊形單元四個節點的撓度近似函數wi(x,y)(i=1,2,3,4)，可表示為：

we={w1(x,y)w2(x,y)w3(x,y)w4(x,y)}T

(8)

其中撓度wi(x,y)(i=1,2,3,4)可表示為：

wi(x,y)=Φiwi(i=1,2,3,4)

(9)

wi=[w1w2w3…wn]T

(10)

式中，Φi為節點i的LSPIM形函數，它由節點i的支撐域點通過LSPIM構成；wi為支撐節點的撓度向量函數；n為節點i的支撐域點的個數。

矩陣Φ4×M由Φi(i=1, 2, 3, 4)組裝得到，列數M等于單元支撐域的節點數。節點支撐域Ω1={1, 2, 3, 4, 5, 6, 7, 8, 9},Ω2={1, 2, 3, 4, 8, 9, 10, 11, 12},Ω3={1, 2, 3, 4, 11, 12, 13, 14, 15} ，Ω4={1, 2, 3, 4, 5, 6, 14, 15, 16}；單元支撐域Ω=Ω1⊕Ω2⊕Ω3⊕Ω4={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16}，如圖2所示。

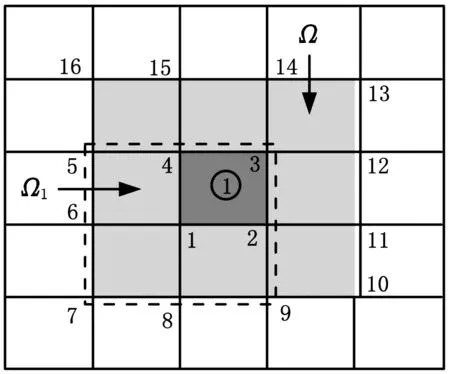
圖2 節點及單元支撐域定義

將式(10),式(9),式(8)代入式(7)中，得到四邊形單元內場點撓度變量的近似形式為：

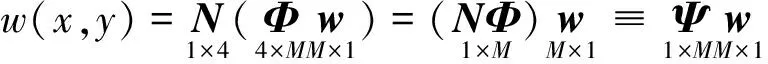
(11)

式中，Ψ為FE-LSPIM的形函數矩陣，定義為：

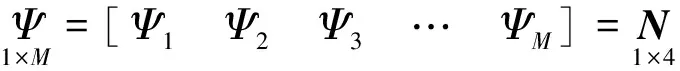
(12)

同理，轉動θx和θy可分別表示為：

(13)

1.2 板的動力學方程

無阻尼板結構動力學方程的Galerkin弱形式為：

∫ΩδκTDbκdΩ+∫ΩδγTDsdΩ+

(14)

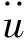
離散后板結構的動力學方程為：

(15)

式中，K=Kb+Ks為板單元剛度矩陣；Kb為彎曲剛度矩陣，Ks為剪切剛度矩陣，M為板單元質量矩陣，Fb為體積力列陣。

剛度矩陣K可表示為：

K=Kb+Ks=

∫Ω(Bb)TDbBbdΩ+∫Ω(Bs)TDsBsdΩ

(16)

式中：

(17)

質量矩陣M可表示為：

(18)

載荷矢量可表示為：

Fb=∫ΩQTbdΩ

(19)

2 板結構-聲場耦合分析

2.1 聲場有限元-最小二乘點插值模型

板結構振動在理想聲場介質中引起的小振幅簡諧聲波、聲壓滿足Helmholtz波動方程：

2p+k2p=0

(20)

式中，p為聲壓；k為波數，k=ω/c；ω為圓頻率；c為聲速。

根據伽遼金原理，聲場問題的弱形式可以寫成如下形式：

∫Ωδp·

(21)

式中，qf表示單位體積的附加載荷。

按照FEM方式將聲場域離散為六面體網格，節點聲壓值近似寫成：

(22)

式中，m為離散單元的節點個數，Nf為標準有限元流體單元的形函數，向量p為六面體單元8個節點的聲壓近似函數pi(x,y)(i=1,2,…,8)。節點聲壓函數pi(x,y)由支撐節點通過LSPIM插值得到，其支撐域范圍如圖3所示。其插值過程與板單元的有限元-最小二乘插值相同，在此不再贅述。

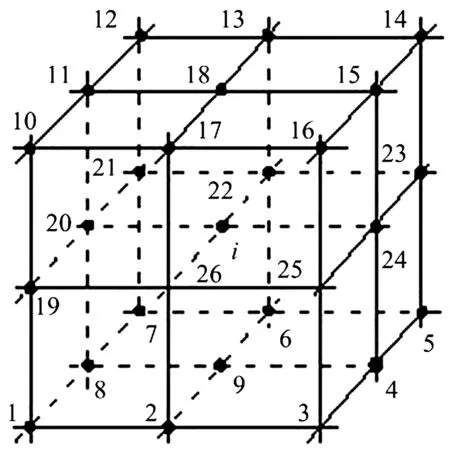
圖3 六面體單元節點i的支撐域點

有限元-最小二乘插值得到的六面體單元內的聲壓近似函數為：

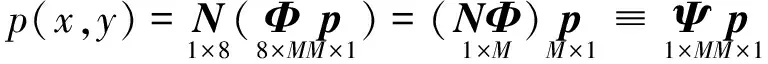
(23)

將式(22)代入(21)中，得到系統的離散方程：

p={p1,p2,…,pn}T

Fs=ρ∫ΩsfΨTΨdΓ

(24)

式中，Kf為聲學剛度矩陣，Bf為聲學梯度矩陣，Mf為聲學質量矩陣，p為節點的聲壓矢量，Fs為載荷向量。

2.2 結構-聲場耦合模型

為實現結構FE-LSPIM模型和聲場FE-LSPIM模型的耦合，如圖4所示，在板結構與聲場的交界面即耦合界面上，應滿足位移和壓力連續的條件。引入界面法向矢量n=nf=-ns，位移連續條件和壓力連續條件可表示為：

(25)

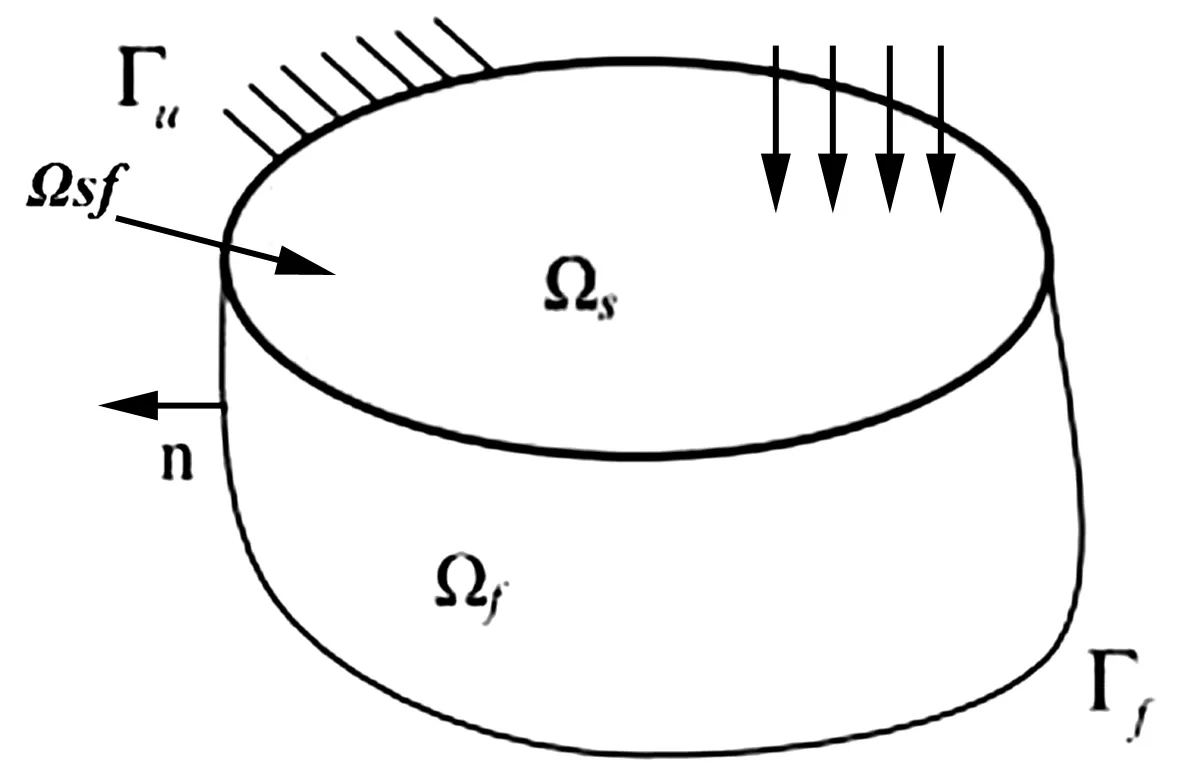
圖4 板結構-聲場耦合系統示意圖

根據式(24)，結構作用在聲場耦合界面Ωsf上的載荷Fs為：

(26)

根據式(19)，聲場作用在結構耦合界面Ωsf上的載荷Ff為：

(27)

式中Ns為結構域單元的形函數，Nf是聲場單元的形函數，這里都采用四邊形等參單元的形函數。

引入耦合矩陣L：

(28)

從結構域的FE-LSPIM模型和聲場的FE-LSPIM模型，可得到結構-聲場耦合的FE-LSPIM/ FE-LSPIM模型：

(29)

假設位移和聲壓為整個時域上的諧波，上式可以寫成：

(30)

3 數值算例

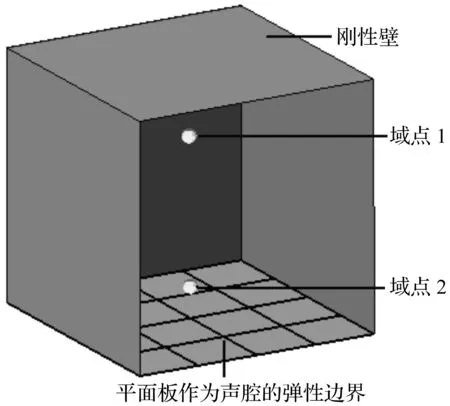
圖5 帶矩形板的六面體結構-聲場耦合模型

圖5所示為六面體附帶矩形板的結構-聲學耦合模型，尺寸為0.414 m×0.314 m×0.360 m。六面體內為空氣域，下表面為矩形平面板結構，尺寸0.414 m×0.314 m，板四邊簡支，其它表面為剛性邊界。矩形平面板材料參數為：彈性模量E=71 GPa，泊松比ν=0.3，密度ρs=2 700 kg/m3，板結構厚度為0.001 m。空氣域聲學參數為：密度ρf=1.21 kg/m3，聲速c=343 m/s。施加在矩形平面板中心點+Z方向的簡諧激勵力幅值為1 N。

本文計算結構-聲場耦合系統問題均通過Matlab程序實現。因為有限元方法網格越密結果越準確，所以參考值通過FEM方法計算較密的網格得到。將平板結構域和聲場域耦合平面按不同網格密度劃分成節點均勻分布的四邊形網格，不同耦合平面網格密度下的結構域和聲域單元數目與單元類型如表1所示。

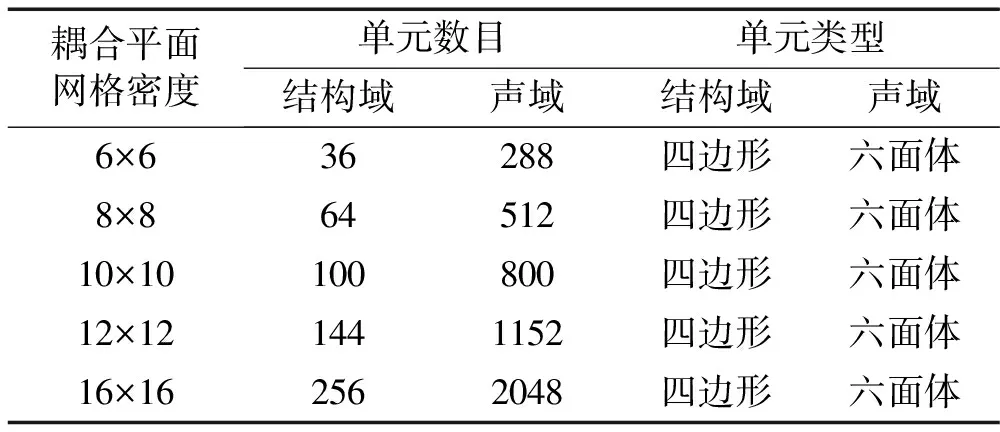
表1 六面體模型的網格劃分

首先應用FE-LSPIM計算矩形彈性板的特征頻率值，并與SFEM和FEM進行對比研究。將矩形彈性板離散成網格密度為8×8的網格模型，用FE-LSPIM、SFEM和FEM分別求得矩形彈性板的前14階固有頻率值，結果如表2所示。表2中參考值由文獻[1]得到。從表2中可以看出，SFEM所得結果略優于FEM所得結果；除了第一階特征頻率外，FE-LSPIM所得結果明顯優于SFEM和FEM所得結果。

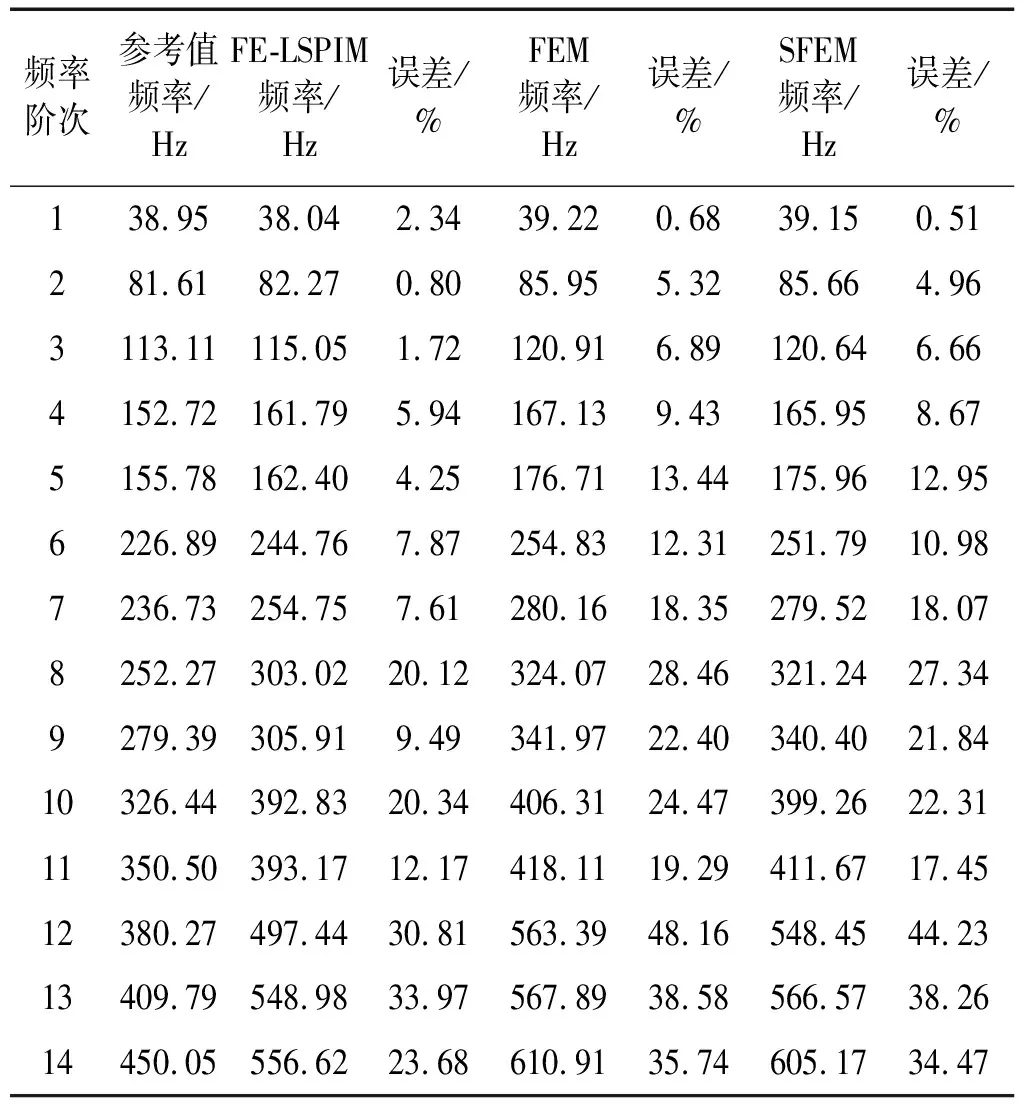
表2 應用FE-LSPIM、SFEM和FEM計算的板固有頻率值

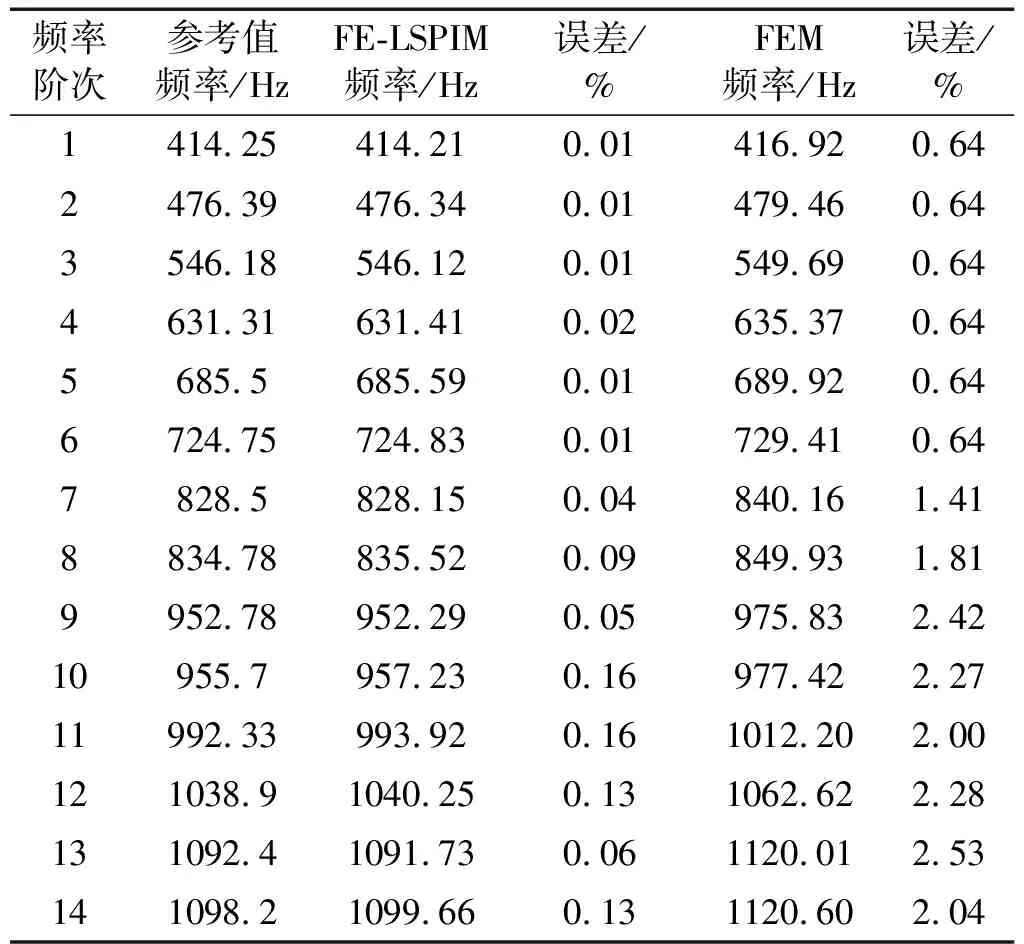
表3 應用FE-LSPIM、FEM計算的空腔固有頻率值

表3所示為用FE-LSPIM計算得到聲腔的前14階非零固有頻率值，耦合平面網格密度為8×8。表中同時給出了用FEM在相同網格模型下計算得到的聲腔的前14階非零固有頻率值以及參考值，參考值由文獻[1]得到。從表3中可以看出，隨著特征頻率階次的增加，由FE-LSPIM和FEM所得結果的誤差呈變大趨勢，但FE-LSPIM所得結果明顯比FEM所得結果更靠近參考值。

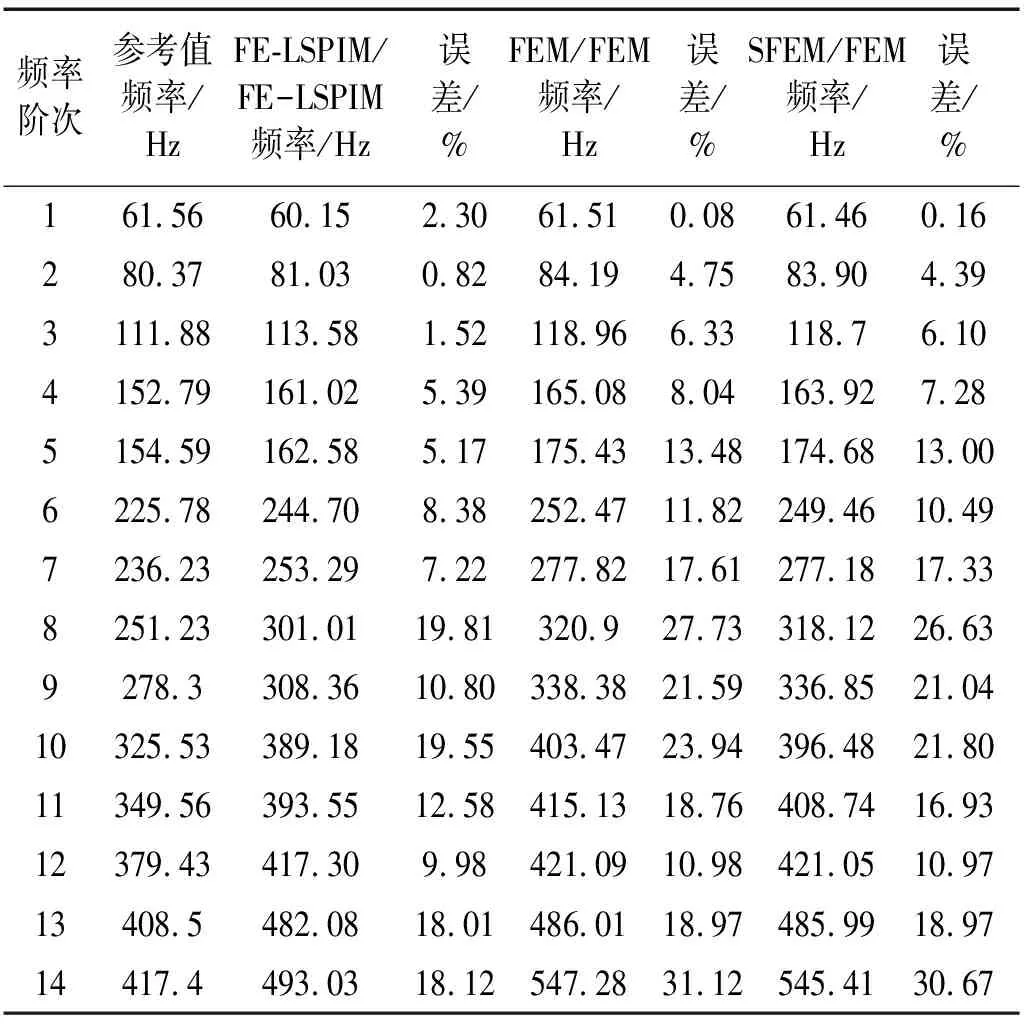
表4 應用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM計算的耦合六面體聲腔固有頻率值

表4所示為用FE-LSPIM/FE-LSPIM計算得到耦合聲腔的前14階非零固有頻率值，耦合平面網格密度為8×8。為了便于對比分析，表中同時給出了用SFEM/FEM、FEM/FEM在相同網格模型下計算得到的耦合聲腔的前14階非零固有頻率值以及參考值，參考值由文獻[1]得到。從表4中可以看出：

(1) 除了第一階特征頻率外，應用FE-LSPIM/FE-LSPIM計算得到耦合聲腔的特征頻率比應用SFEM/FEM、FEM/FEM計算所得結果更靠近參考值；

(2) 隨著特征頻率階次的增加，FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM的計算結果更加遠離參考值，計算誤差整體呈變大趨勢，但是在大多數情況下，FE-LSPIM/FE-LSPIM計算結果的誤差明顯小于SFEM/FEM和FEM/FEM計算結果的誤差，相對能取得較高精度的結果。

為分析單元尺寸對FE-LSPIM/FE-LSPIM耦合聲場計算結果的影響，將平板結構域和聲場域耦合平面按不同網格密度劃分成節點均勻分布的四邊形網格，網格密度分別取：6×6、8×8、10×10、12×12、16×16，相應的結構域單元數和聲域單元數如表1所示。為評價FE-LSPIM/FE-LSPIM的計算效果，同時給出FEM/FEM和SFEM/FEM的聲壓計算結果進行對比研究，參考值通過NASTRAN計算耦合平面網格密度為50×50的模型得到。表5和表6分別表示激振頻率為150Hz及230Hz時應用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM計算的域點1的聲壓值。

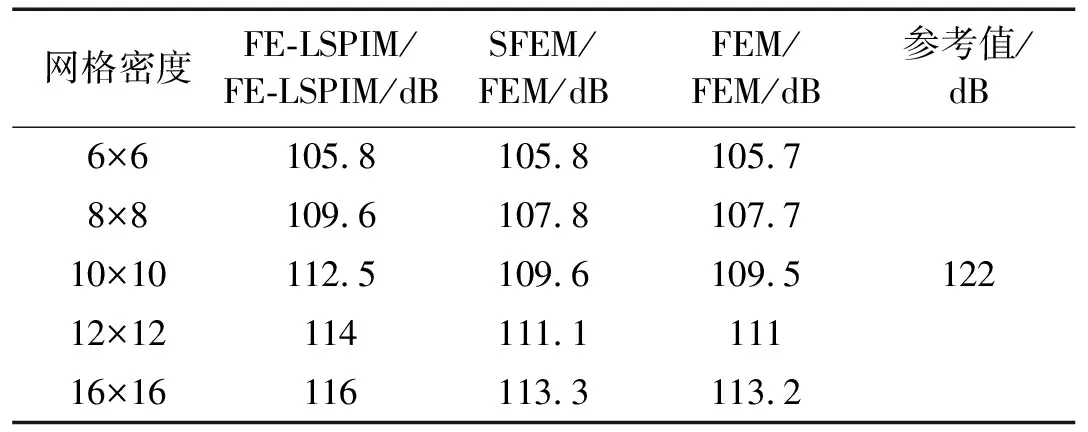
表5 激振頻率為150 Hz時域點1聲壓

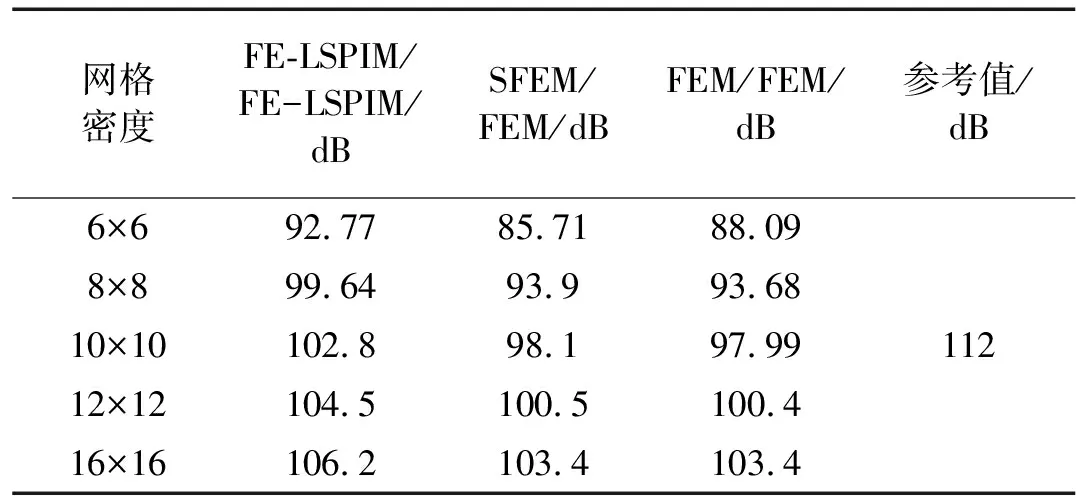
表6 激振頻率為230 Hz時域點1聲壓

綜合表5和表6可知：隨著網格密度的增加(即單元尺寸的減少)，FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM的計算結果都逼近參考結果，說明FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM都是收斂的，且FE-LSPIM/FE-LSPIM比SFEM/FEM和FEM/FEM收斂更快。

為了進一步評價FE-LSPIM/FE-LSPIM 分析結構-聲場耦合問題的效果，本文計算了域點1和2的聲壓頻率響應，計算頻率范圍為20～320 Hz，并給出了SFEM/ FEM和FEM/ FEM的計算結果作為對比，參考值通過FEM/ FEM計算耦合平面網格密度為16×16的模型得到。

圖6和圖7分別表示耦合平面網格密度為8×8時三種方法所計算的域點1和2的聲壓頻率響應曲線。從圖中可以看出：通過SFEM/FEM、FEM/FEM和FE-LSPIM/FE-LSPIM所得的聲壓頻率響應曲線趨勢與參考值相同，由于網格尺寸較大，計算結果均與參考值相差較大，但與SFEM/FEM和FEM/FEM相比，FE-LSPIM/FE-LSPIM的計算結果更接近參考值。這表明FE-LSPIM/FE-LSPIM比SFEM/ FEM和FEM/ FEM更精確，在同等粗糙的網格模型下計算結果更好。

圖8為不同網格密度下用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM計算得到的域點1聲壓頻率響應曲線，計算頻率范圍為20～320 Hz。FE-LSPIM/FE-LSPIM計算的耦合平面網格密度為8×8； SFEM/FEM和FEM/FEM計算的耦合平面網格密度分別取10×10和12×12。從圖中可以看出，隨著網格密度的增加，計算結果越準確，聲壓頻率響應曲線整體向左移動靠近參考值。FE-LSPIM/FE-LSPIM在網格密度為8×8時的計算結果與SFEM/FEM和FEM/FEM在網格密度為12×12時的計算結果相接近，從而進一步說明了對粗糙網格模型，FE-LSPIM/FE-LSPIM比SFEM/ FEM和FEM/ FEM的計算精度更高。

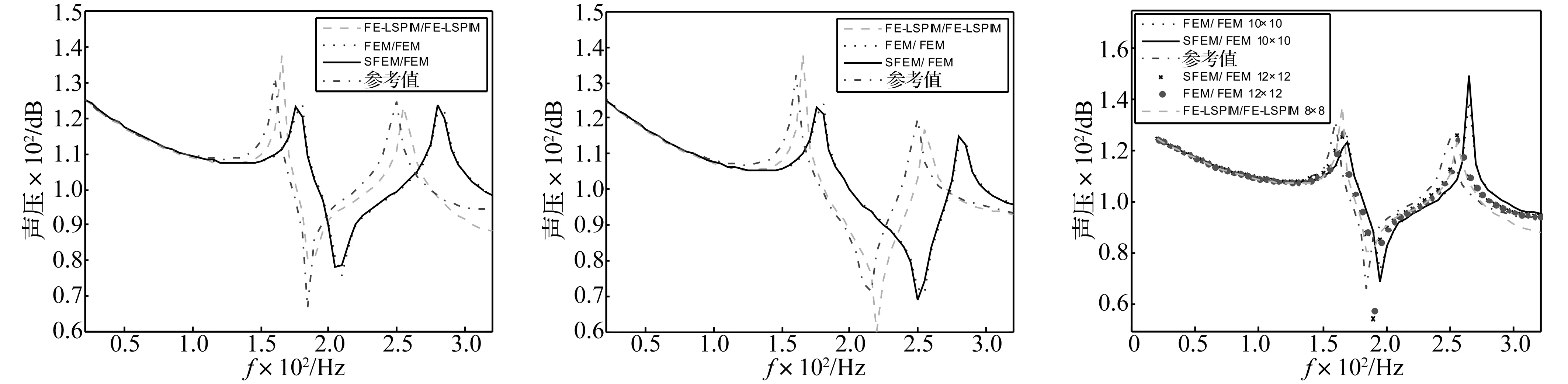
圖6 域點1聲壓頻率響應曲線

4 結 論

本文將FE-LSPIM推廣用于Mindlin-Reissner板結構動力學和三維聲場分析，提出用于板結構-聲場耦合問題分析的FE-LSPIM/FE-LSPIM，推導了FE-LSPIM/FE-LSPIM分析板結構-聲場耦合問題的計算公式。并以一六面體聲場-結構耦合模型為研究對象進行分析，研究結果表明：FE-LSPIM/FE-LSPIM能很好地應用于板結構- 聲場耦合分析中，其計算結果比SFEM/ FEM和FEM/ FEM收斂快，并且對單元網格尺寸要求比SFEM/ FEM和FEM/ FEM低，在計算較大網格尺寸模型時，能得到比SFEM/ FEM和FEM/ FEM更高的計算精度。因此，用FE-LSPIM/FE-LSPIM分析板結構-聲場耦合問題可以減小計算規模、節省計算時間，具有良好的工程應用前景。

[1]He Z C, Liu G R, Zhong Z H, et al. A coupled edge-/face-based smoothed finite element method for structural-acoustic problems[J]. Applied Acoustics, 2010, 71: 955-964.

[2]He Z C, Liu G R, Zhong Z H, et al. Coupled analysis of 3D structural-acoustic problems using the edge-based smoothed finite element method/finite element method[J]. Finite Elements in Analysis and Design, 2010, 46: 1114-1121.

[3]Atalla N, Bernhard R J. Review of numerical solution for low-frequency structural-acoustic problems. Applied Acoustics, 1994(43):271-249.

[4]姚凌云,于德介,臧獻國. 殼結構聲場耦合分析的光滑有限元-有限元法[J]. 中國機械工程，2010，21(15)：115-120.

YAO Ling-yun, YU De-jie, ZANG Xian-guo. Analysis of shell structural-acoustic coupling based on smoothed finite element and finite element method[J]. Chinese Mechanical Engineering, 2010，21(15)：115-120.

[5]Melenk J M, Babu ska I. The partition of unity finite element method：basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1-4)：289-314.

[6]Wenterodt C, Estorff O V. Dispersion analysis of the meshfree radial point interpolation method for the Helmholtz equation[J]. International Journal for Numerical Methods in Engineering, 2009,77：1670-1689.

[7]Rajendran S, Zhang B R. A “FE-Meshfree” QUAD4 Element for Free-vibration Analysis[J]. Computer Methods in Applied Mechanicals and Engineering, 2007, 197: 3595-3604.

[8]Rajendran S, Zhang B R. A “FE-Meshfree” QUAD4 Element Based on Partition of Unity[J]. Computer Methods in Applied Mechanicals and Engineering, 2007, 197: 128-147.

[9]姚凌云,于德介,臧獻國. 聲學數值計算的有限元-最小二乘點插值法[J]. 中國機械工程，2010，21(23)：2816-2820.

YAO Ling-yun, YU De-jie, ZANG Xian-guo. A finite element-least square point interpolation method for acoustic numerical computation[J]. Chinese Mechanical Engineering, 2010，21(23)：2816-2820.