彈性波在對稱準周期結構固/液聲子晶體中的傳播

肖緒洋，陳潤平，夏繼宏，席 鋒

(1.重慶文理學院 電子電氣工程學院，重慶 永川 402160; 2.重慶工商大學 計算機科學與信息工程學院，重慶 400067)

近年來，復合周期結構對經典波傳播特性的調控引起了人們廣泛的關注。聲子晶體(Phononic crystal, PnC)是由彈性介質周期交替排列形成的復合材料[1-3]。彈性波在其中傳輸時，由于結構的周期性而形成聲子帶隙[4-7](Acoustic Band Gap, ABG)，使頻率落入聲子帶隙的彈性波被禁止傳播。由于利用聲子晶體的帶隙能實現對彈性波的有效控制，故在聲濾波、隔離噪聲、減振，以及聲學功能器件方面有著廣泛的應用前景。

在對周期性結構的聲子晶體研究中，已經發現聲子晶體與光子晶體類似，存在聲子局域態、超晶格折疊性、負折射等現象[8-10]。聲波在周期結構聲子晶體中的傳輸特性已有深入研究[11-13]，對準周期結構聲子晶體對彈性波的調控特性也有了新的認識[14-16]。現有對準周期結構聲子晶體多基于彈性波在固體介質聲子晶體的研究。通常研究固液介質聲子晶體是將固體薄片或固體柱體浸入液體或空氣中[17-18]。理想情況下，不考慮液體的黏滯效應時，只能傳遞彈性縱波。而某些介質常態時為固體，也只能傳遞彈性縱波[19]，如聚乙烯，石英等，從這一角度考慮，也可當成“液”體介質對待。由固體介質和這類“液”體介質構成的聲子晶體能脫離液體介質環境而獨立存在，為其實際利用提供了方便。準周期結構是介于周期結構和無序結構之間的一種結構，相比于周期結構存在局域失諧。這種局域失諧結構產生的聲子局域化現象與周期結構中由引入缺陷體產生的局域失諧有何區別,本文針對固“液”介質的Fibonacci序列的對稱準周期結構聲子晶體，研究彈性波在這種無序結構中的帶隙特征和局域化現象以及入射角對聲子晶體帶隙的影響。

1 對稱準周期結構聲子晶體

一維Fibonacci序列準周期固液介質聲子晶體由固體介質A和液體介質B構成。Fibonacci序列由迭代關系生成，設Fj={Fj-1,Fj-2} 當j≥2時，其中F0={A} 和F1={AB}。對稱準周期結構表示為Sj=FjF’j，其中F’j為與Fj對應的對稱結構。當j=5時的對稱準周期結構聲子晶體如圖1所示，A為固體介質，B為液體介質，其厚度分別為da，db。

圖1 對稱準周期結構聲子晶體

在不考慮液體介質的橫向粘滯效應情況下，液體介質中不能傳輸橫波，只能傳輸縱波。在相鄰固液介質的界面上，根據位移和應力在界面的連續條件，得到在相鄰界面上前行波和后行波的振幅關系為：

(1)

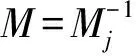
(2)

式中;

和

(3)

式中:θ為聲波在端面的入射角，θjT和θjL分別為橫波和縱波在固體介質面上的入射角，θj+1為聲波在液體界面上的入射角，均由Snell定律確定；λ和μ分別為固體介質的拉梅常數，下標L表示縱波，T表示橫波。

波通過厚度為dj的介質后，僅有相位發生變化，相應的傳輸矩陣為：

(4)

在一個周期內的傳輸矩陣可寫為：

(5)

進而可得到整個對稱準周期聲子晶體的傳輸矩陣，并可進一步求得透射率和反射率。

2 數值結果和討論

固體介質A和液體介質B分別為鋁和聚乙烯，相應的物理參數為：ρa=2 700 kg/m3,cLa=6 350 m/s，cTa=3 080 m/s，ρb=920 kg/ m3,cb=2 000 m/s，介質厚度da=cLa/4f0,db=cb/4f0，f0(=10 kHz)為入射彈性波的中心頻率。環境介質為水，ρ0=1 000 kg/ m3,c0=1 480 m/s。利用傳輸矩陣法進行數值計算，并分析彈性波在不同準周期序列的對稱結構聲子晶體中的傳輸特性。

2.1 彈性波正入射

中心頻率為f0彈性縱波正入射，序列分別為S4、S5、S6和S7的準周期對稱結構聲子晶體的透射特性如圖2(a)、(b)、(c)和(d)所示。從圖中看出，在中心頻率f0處出現了局域諧振模，頻率半高寬僅為幾Hz；其帶隙比由A和B構成的周期聲子晶體帶隙要寬[19]，且隨著序列的增加，帶隙略有展寬。實際上，在透射譜中，中心頻率奇數倍處都將出現諧振模，這與周期結構中心缺陷的情況相同[21]。為了方便，我們僅討論一級聲子帶隙。從圖2(a)、(b)和(c)的插入圖發現，除了中心頻率處的局域諧振，還在中心頻率兩側對稱的出現兩條次級局域諧振模，其頻率半高寬較中心局域諧振模頻率半高寬窄。序列越大，局域諧振越強，因而品質因子(中心頻率/頻率半高寬)越高。

由于低序列的準周期聲子晶體，主要表現出結構的非周期性，相當于在周期結構中加入多個缺陷層。因此，彈性波從準周期結構聲子晶體透射后將產生局域諧振模。當準周期序列增大時，準周期聲子晶體的無序性降低，而有序性增強，將主要表現出周期結構的特性。在所討論的對稱準周期結構聲子晶體中，在對稱面兩側(對稱中心處)，奇數序列為介質B，偶數序列為介質A。由此可以把這兩層介質看做缺陷體，又因為處于結構中心處，因而在透射譜的帶隙中心應出現局域諧振模，這與局域理論完全相符。

圖2(d)所示為彈性波在S7序列中的透射譜。在該透射譜中，只在中心頻率處出現一條局域諧振模，但其頂部不再平坦，變為鋸齒狀。由于結構層數增多使局域諧振增強，同時對局域聲子的選頻作用也增強，使次級局域諧振模向中心頻率靠近而合并，次級局域諧振模消失。

在圖2(b)、(c)和(d)中，在0.3f0和1.7f0附近出現帶邊諧振，且隨著序列的增加，帶邊的諧振增強。而圖2(a)中，由于S4序列(ABAABABAABABAABA)相當于在周期結構中引入三個缺陷層，其透射譜中出現三個局域諧振模，帶邊沒有局域諧振。另外，從圖中對比還發現，序列越高，中心諧振模的帶邊越陡。這是因為序列增加時，系統結構的層數增加更快，諧振越強，從而使聲子局域頻率的帶寬變窄。

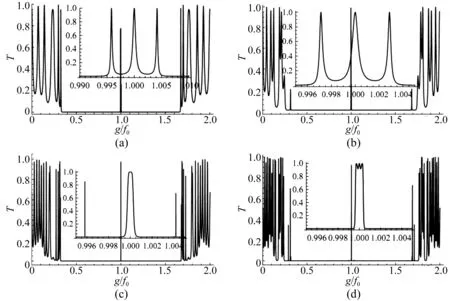
圖2 正入射時不同對稱序列準周期聲子晶體的透射譜

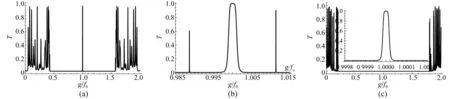
圖3 不同介質時S6序列的透射譜

彈性波在由不同介質構成的S6序列中的透射如圖3所示。圖3(a)和(b)為液體介質B為黏合劑(ρb=1 738 kg/ m3,cb=2 240 m/s)，固體介質A為鋁時的彈性波透射譜。與圖2(c)相比，聲子帶隙變窄，帶邊局域諧振減弱。圖3(c)為液體介質B為聚乙烯，固體介質A為鋼(ρa=7 800 kg/m3,cLa=5 850 m/s，cTa=3 230 m/s)時彈性波的透射譜。其帶隙增寬，帶邊局域諧振更強。透射譜變化的主要原因在于介質的波阻抗(Z=ρcL)不同。鋁和聚乙烯的波阻抗比為ZA/ZB=9.32，鋁和黏合劑的波阻抗之比為ZA/ZB=4.40，鋼和聚乙烯的波阻抗之比為ZA/ZB=24.80。固液介質的波阻抗越大，帶隙越寬，局域諧振場強。當固體介質為鋼時，由于介質的波阻抗相差太大，只有中心處的局域諧振能透射，抑制了次級諧振。

2.2 彈性波斜入射

為清晰認識彈性縱波在該對稱準周期固液介質聲子晶體中的傳輸特性，需要研究彈性縱波斜入射時縱波的透射譜。由Snell定律，固液介質界面上的臨界角為θc=arcsin(cb/cLa)=18.4°。在固液界面上彈性波的入射角大于時由于發生全反射而不能在結構中傳輸。當彈性縱波以5°斜入射S4、S5、S6和S7的對稱準周期結構聲子晶體時，相應的透射譜如圖4(a)、(b)、(c)和(d)所示。從圖中看出，斜入射時，一級帶隙略微展寬，并向高頻區移動，這一特點與周期結構聲子晶體相同[16]。同時在頻率2.00f0～2.10f0內出現次級帶隙。

另外，一級帶隙的帶間諧振和帶邊諧振以及級次帶隙的帶間諧振隨著序列的增加顯著增強。從圖中看出，固液聲子晶體對彈性波入射角很敏感，彈性波以較小的角度入射，就能使聲子帶隙發生很大的變化。彈性波斜入射時，透射譜發生頻移，使原來在中心頻率處的局域諧振模也向高頻區移動，出現在1.07f0附近。當彈性波以15°斜入射S7序列的透射如圖4(e)所示。此時只有低頻彈性波透射，其頻率上限約為0.54f0，頻率大于此值的彈性波在端面被全反射。從插入圖中還可以算出，在0.26f0～0.31f0間出現一個低頻帶隙。次級帶隙產生的原因在于，入射的彈性縱波在固體介質中將有一部分轉換為橫波，而這一部分橫波是不能在液體介質中傳播的。

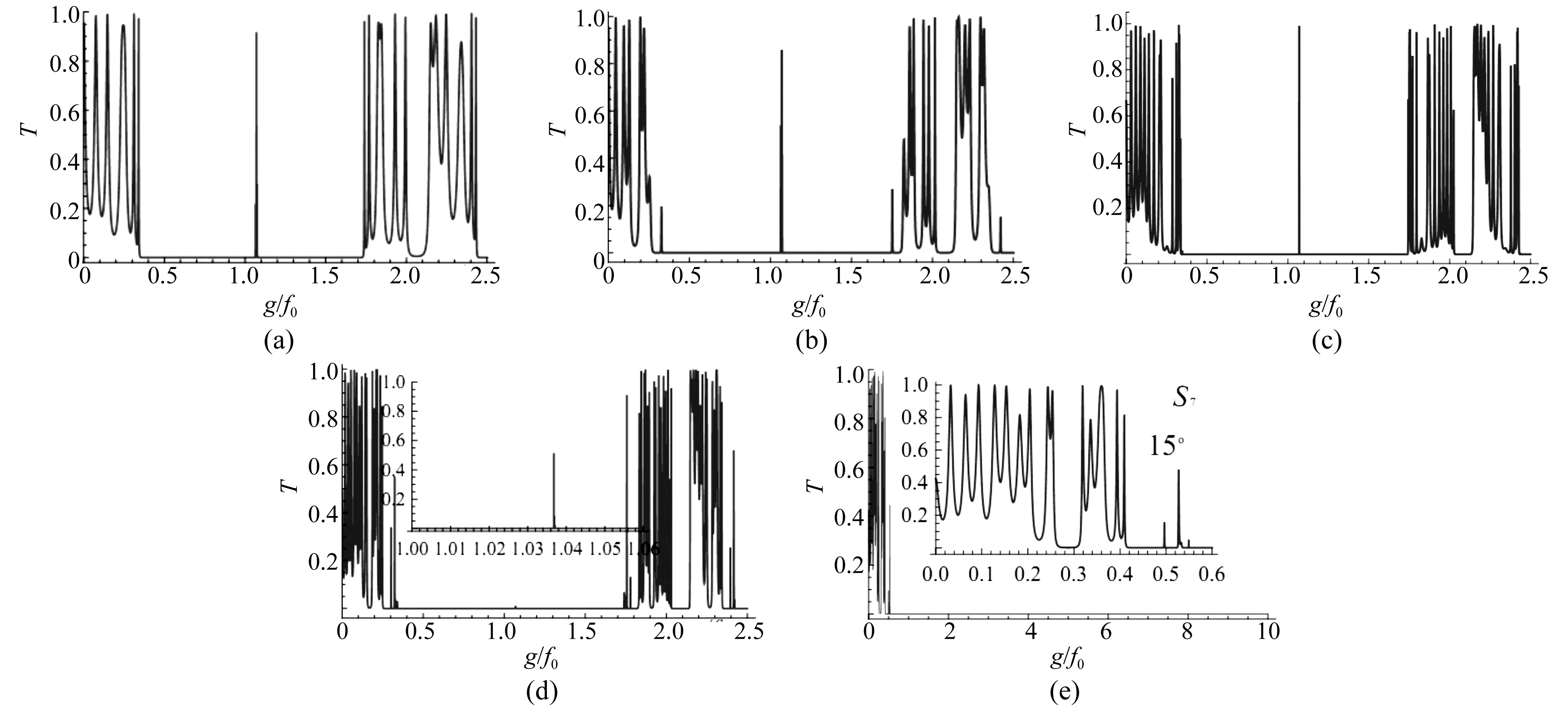
圖4 斜入射時不同對稱序列準周期聲子晶體的透射

3 結 論

本文基于Fibonacci準周期序列，提出了一維固液介質聲子晶體的對稱準周期結構。利用傳輸矩陣法，研究了彈性縱波在其中的透射特性。數值研究的結果表明，彈性波正入射時，該對稱準周期固液聲子晶體的帶隙中，由于結構的失諧，在中心頻率附近出現局域諧振模，其頻率帶寬僅為幾Hz，因此，利用該準周期結構聲子晶體獲得的局域諧振模，比通過引入缺陷結構得到的諧振模有更高的品質因子。根據這一特點，利用不同的對稱準周期序列，可實現超窄帶的多通道濾波。當彈性波以較小的角度斜入射時，聲子帶隙以及帶隙中的局域諧振模都略微向高頻方向移動，同時出現次級聲子帶隙。

利用彈性波在對稱準周期結構聲子晶體中的局域失諧，得到品質因子很高的局域諧振模，以實現超窄帶聲子濾波，這對設計和制備聲波器件具有重要意義。

[1]Kushwaha M S. Acoustic band structure of periodic elastic composites[J]. Phys. Rev. Lett. 1993, 71(13):2022-2025.

[2]Jesen J S, Phononic band gaps and vibrations in one-and two-dimensional mass-spring structures[J]. Journal of Sound and Vibration, 2003, 266(5)：1053-1078.

[3]Wang Gang, Yu Dian-long, Wen Ji-hong. One-dimensional phononic crystals with locally resonant structures[J]. Physics Letters A, 2004, 327(5-6)：512-521.

[4]Sigalas M M, Soukoulis C M. Elastic-wave propagation through disordered and/ or absorptice layered systems[J]. Phys. Rev. B, 1995,51(5): 2780-2789.

[5]Liu Z Y, Zhang X X, Mao Y W, et al. Locally resonant sonic materials[J]. Science, 2000, 289: 1734-1736.

[6]Wang G, Wen X S, Wen J H, et al. Two-dimensional locally resonant phononic crystals with binary structure[J]. Phys. Rev. Lett. 2004, 93(15):154302.

[7]舒海生,劉少剛,王威遠,等.集中質量邊界條件下聲子晶體桿的縱向振動傳遞特性研究[J]. 振動與沖擊,2012,31(19):113-117.

SHU Hai-sheng, LIU Shao-gang,WANG Wei-yuan, et al. Transmission characteristic of longitudinal vibration of a phononic crystal rod with concentrated mass boundary condition[J]. Journal of Vibration and Shock,2012,31(19):113-117.

[8]溫激鴻，王剛，劉耀宗，等，基于集中質量法的一維聲子晶體彈性波帶隙計算[J].物理學報，2004，53(10)，3384-3388.

WEN Ji-hong, WANG gang, LIU Yao-zhong, et al. Lumped-mass method on calculation of elastic band gaps of one-dimensional phononic crystals[J], Acta Physica Sinica, 2004，53(10)，3384-3388.

[9]吳福根，劉有延，二維周期性復合介質中聲波帶隙結構及其缺陷態[J], 物理學報，2002，51(7)，1434-1438.

WU Fu-gen, LIU You-yan. Acoustic band gaps and defect states in two-dimensional composite materials[J]. Acta Physica Sinica, 2002, 51(7):1434-1438.

[10]Peng Pai, Qiu Chun-yin, Ding Yi-qun, et al, Acoustic tunneling through artificial structures: From phononic crystals to acoustic metamaterials[J].Solid State Communications, 2011, 151(5): 400-403.

[11]Hou Zhilin, Badreddine M A, Transmission property of the one-dimensional phononic crystal thin plate by the eigenmode matching theory[J]. Journal of Phys. D: Appl. Phys. 2008, 41(9): 095103.

[12]Khelif A, Djafari-Rouhani B, Vasseur J O, et al, Transmission and dispersion relations of perfect and defect-containing waveguide structures in phononic band gap materials[J]. Phys. Rev. B, 2003,68(2):024302.

[13]宿星亮, 高原文. 含有功能梯度材料的一維聲子晶體彈性波帶隙研究[J]. 固體力學學報，2012，33(1):75-80.

SU Xing-liang, GAO Yuan-wen. Research on band gap of one-dimensional phononic crystals with functionally graded materials[J]. Chinese Journal of solid mechanics, 2012, 33(1): 75-79.

[14]曹永軍, 董純紅, 周培勤.一維準周期結構聲子晶體透射性質的研究[J]. 物理學報，2006，55(12):6470-6475.

CAO Yong-jun, DONG Chun-hong, ZHOU Pei-qin. Transmission properties of one-dimensional qusi-periodical phononic crystal[J]. Acta Physica Sinica, 2006, 55(12): 6470-6474.

[15]楊立峰, 王亞非, 周鷹. 一維壓電Fibonacci類準周期聲子晶體的傳輸特性[J]. 物理學報，2012，61(10):107702-6.

YANG Li-feng, WANG Ya-fei, ZHOU Ying. The transmission properties in one-dimensional piezoelectric Fibonacci-class quasi-periodical phononic crystals[J]. Acta Physica Sinica, 2012, 61(10):107702-6.

[16]Wang Gang, Wen Ji-hong, Wen Xi-sen, Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap[J]. Phys. Rev. B, 2005, 71(10)：104302-5.

[17]劉啟能. 固流結構聲子晶體中彈性波能帶的色散研究[J]. 人工晶體學報，2009，38(1):107-112.

LIU Qi-neng. Dispersive study on the photonic bandgap of solid and fluid phononic crystal[J]. Journal of Synthetic Crystals, 2009, 38(1):107-112.

[18]Romero-Garcia V, Sanchez-Perez J V, Castineira-lbanez S, et al, Evidences of evanescent Bloch waves in phononic crystals[J]. Appl. Phys. Lett. 96(12), 2010, 124102.

[19]Rose J L. 固體中的超聲波[M]. 何存富, 吳斌, 王秀彥譯. 北京: 科學出版社, 2004.

[20]劉啟能. 一維聲子晶體的傳輸特性[J]. 人工晶體學報，2008，37(1):179-182.

LIU Qi-neng, Transfer characteristic of one-dimensional phononic crystal[J]. Journal of Synthetic Crystals, 2008, 37(1):179-182.

[21]朱 敏，方云團，沈廷根. 一維聲子晶體的缺陷態的研究[J]. 人工晶體學報，2005，34(3):536-541.

ZHU Min, FANG Yun-tuang, SHEN Ting-gen, Study on one-dimensional phononic crystal with defects[J]. Journal of Synthetic Crystals, 2005, 34(3):536-541.