基于廣義DF法的參數可調二階滑模抖振特性分析
申 宇,仇原鷹
(1.西南大學 計算機與信息科學學院,重慶 400715;2.西安電子科技大學 電子裝備結構設計教育部重點實驗室,西安 710071)
非線性系統中普遍存在自激振蕩現象[1]。而該現象在滑模控制中尤為引人關注,即滑模控制的抖振。抖振對滑模控制系統的影響主要表現為:較大的抖振幅度將降低控制精度;抖振頻率與系統諧振頻率相近時易引發系統共振;過快的抖振頻率可能超出控制器允許的最大切換速率。如文獻[2]中,Bang-Bang控制器引入的抖振頻率就必須小于磁流變阻尼器允許的電壓切換速率,而該文獻并未提出如何調節抖振頻率。因此,如何估算和調節系統的抖振特性(即抖振幅度An和抖振角頻率ωn)成為滑模控制的重要研究問題。
趨近率滑模[3]是滑模控制的典型代表,學者們通常在時域上研究如何抑制切換控制所引入的抖振,利用全部狀態變量設計滑模面參數,再設計“準滑動模態”或“低通濾波器”[4]來削弱抖振。由于時域分析法的局限性,學者們一般通過仿真實驗曲線來評估對抖振的抑制效果,但這樣的設計思路存在以下問題:① 在工程應用中很難測量全部狀態變量;② 一般采取定性的方法分析抖振的抑制效果,無法準確計算抖振特性;③ 很難找出抖振特性與控制系統參數之間的對應關系,因而無法靈活調節抖振特性。
由于滑模切換函數的非連續性和多樣性,僅采用時域法分析滑模抖振特性已力不從心。因此,有學者借助頻域經典描述函數(DF)法來分析該問題。Oliveira等[5]利用經典DF法為不確定系統設計的滑模控制器,通過調整G(s)與-1/N(A)幅相頻率特性曲線相交位置實現抖振特性的定量調節,并提高了系統魯棒性;Huang等[6]運用經典DF法分析了滑模控制器的穩定性和極限環,并研究各種切換函數對抖振特性的影響;Boiko近十年時間,在經典DF法基礎上提出了滯環控制器[7]、輸出反饋纏繞控制器[8]、二階滑模控制器[9-10]的抖振特性計算和調節方法。但是基于經典DF法的滑模抖振研究仍然存在一些問題:只能分析滑模面的抖振特性而無法分析系統各狀態變量的抖振特性;只能分析與振幅A相關的簡單描述函數N(A),而不能分析與振幅A和角頻率ω相關的復雜描述函數N(A,ω)。
為更完善地研究滑模控制的抖振特性,本文將以一類參數可調2-SMC為研究對象,首先利用經典DF法,找到系統輸出量y(t)的抖振特性隨控制參數變化的規律;接著針對復雜非線性環節提出廣義DF法,以估算抖振特性并分析抖振穩定性;最后利用廣義DF法估算系統狀態變量的抖振特性。
1 控制系統設計
考慮如圖1所示的自治反饋控制系統,其中被控對象G(s)=G1(s)G2(s),且G1(s)與G2(s)的零極點均位于左半平面或虛軸上;x1,x2為待分析的狀態變量;u為被控系統輸入量;y為被控系統輸出量且y=x1。
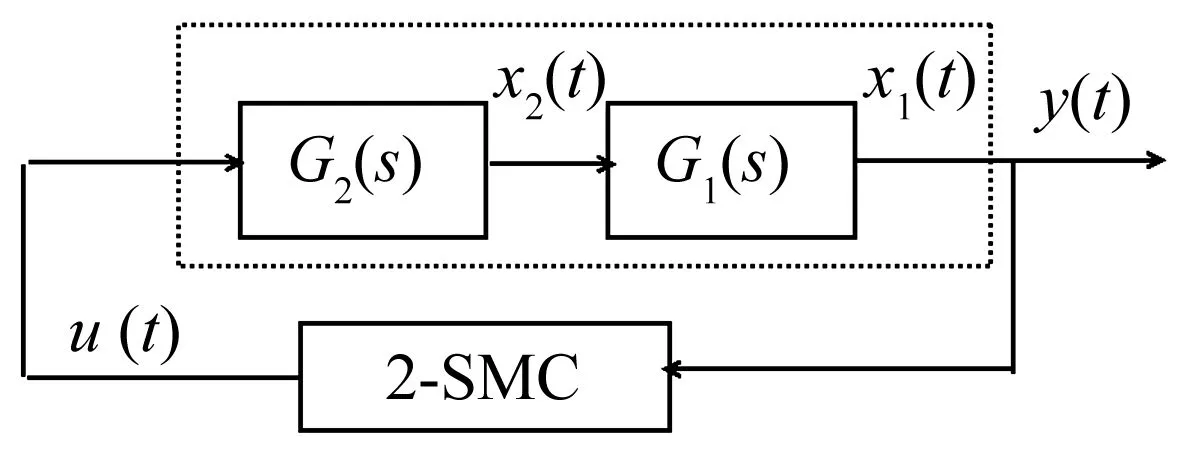
圖1 二階滑模控制系統
圖1中2-SMC為可調二階滑模控制器[11],其輸出控制量表示為
u(t)=-α(t)Msign(σ(t))
(1a)
(1b)
σ(t)=y(t)-βyM(t)
(1c)
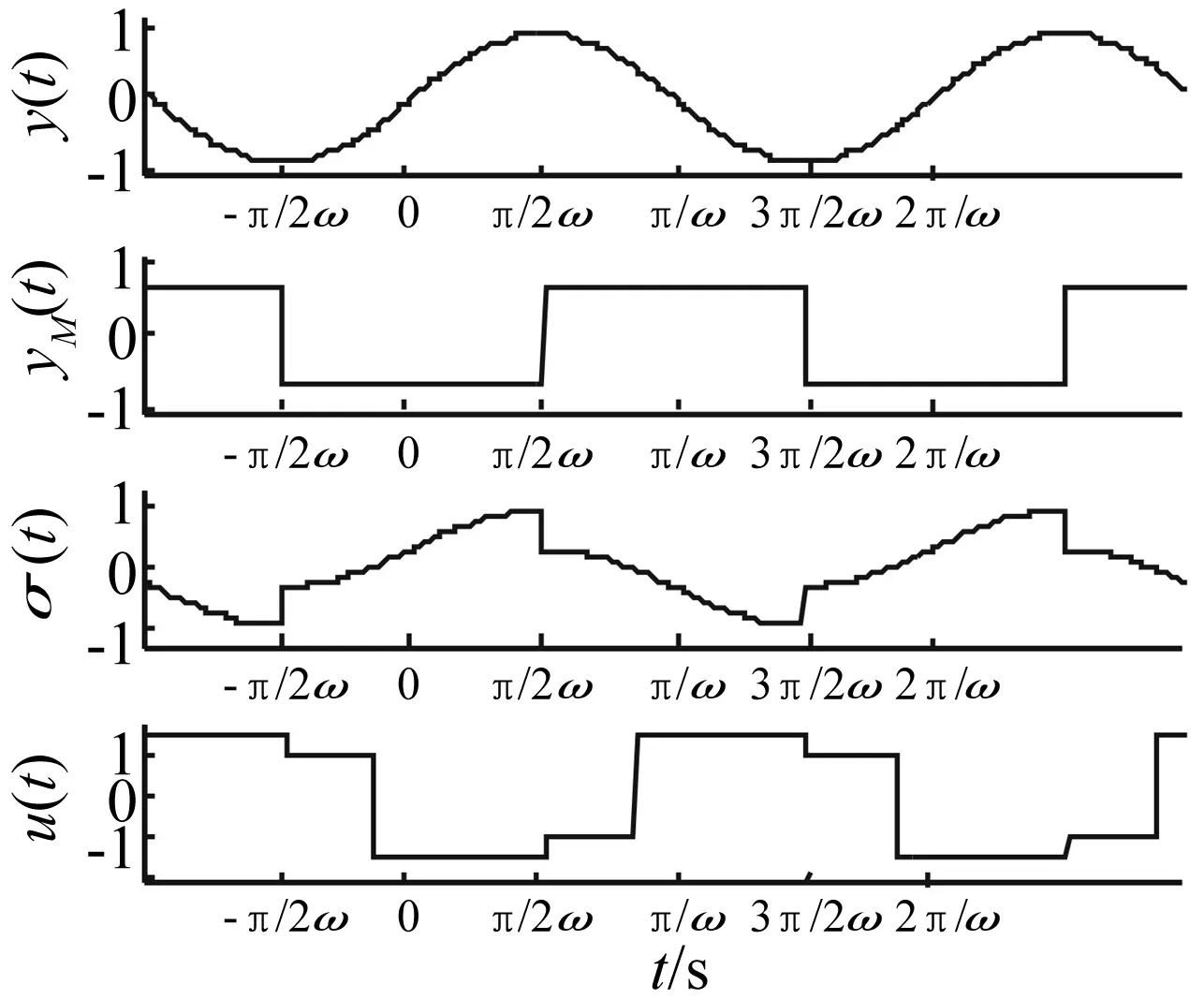
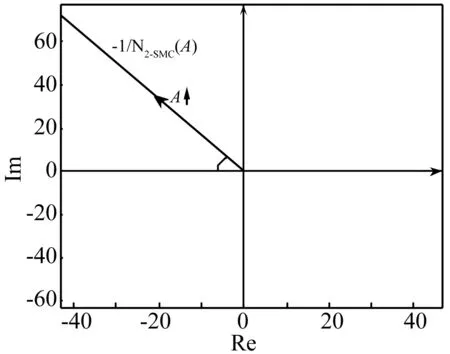
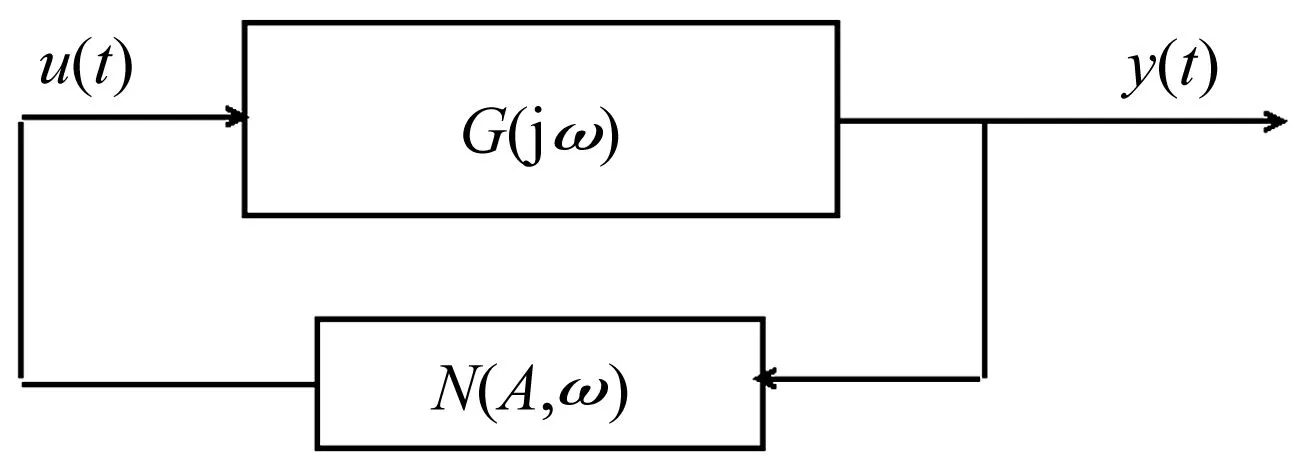
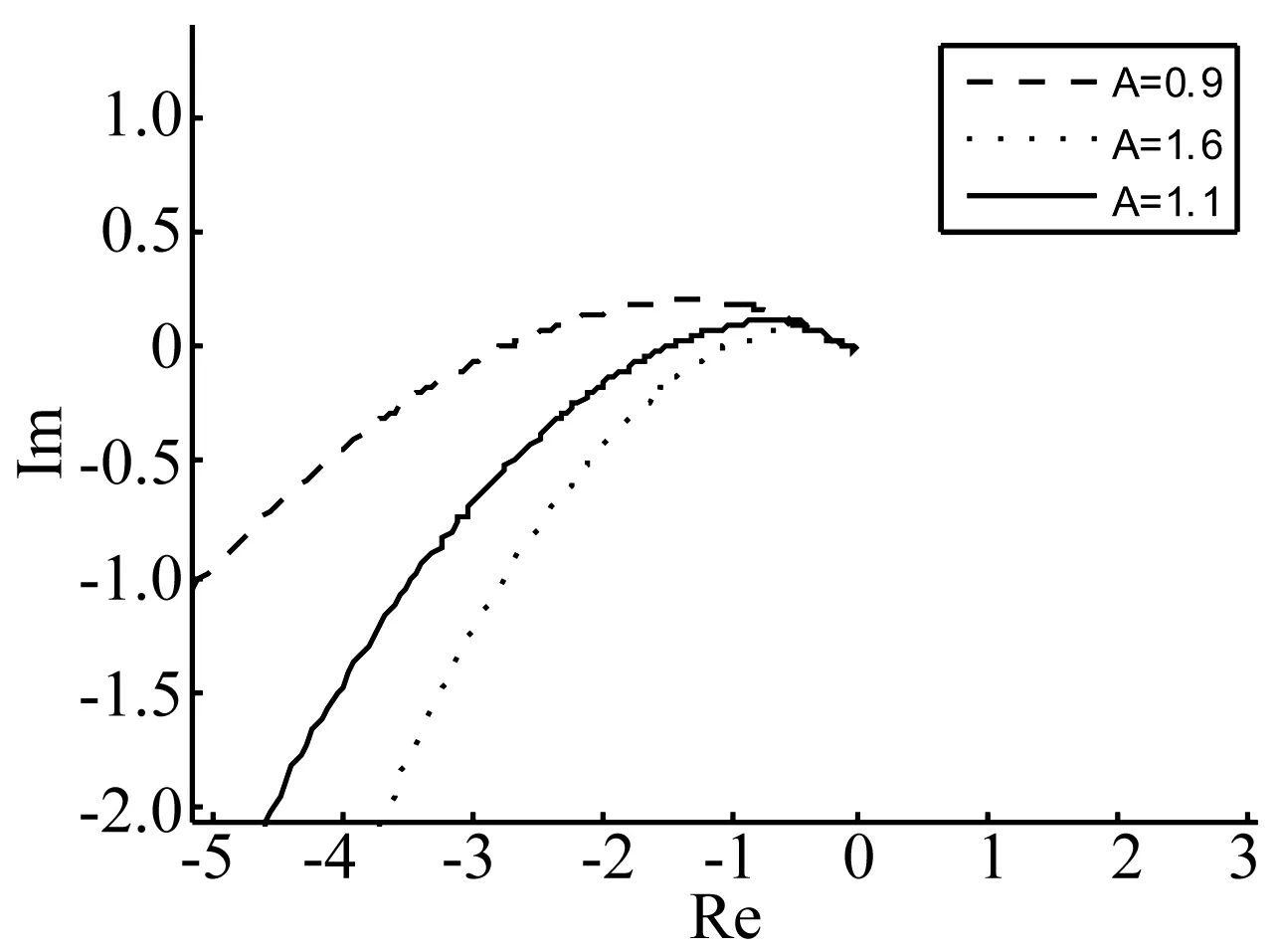
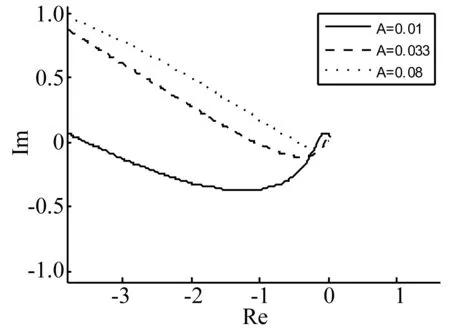
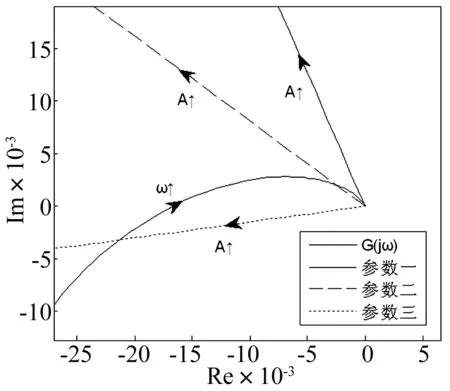
式中:M為控制器增益;α*>0;β∈(0,1];yM(t)定義為輸出量y(t)的最新極值,并設定yM(0)=0。yM(t)可理解為:若存在多個時刻td1 則 本小節將利用經典描述函數法,分析控制系統的穩定性和輸出量抖振特性。首先計算2-SMC對應的負倒描述函數-1/N1(A),在2-SMC的輸入端施加正弦信號Asin(ωt),并依次得到對應的yM(t)、σ(t)和控制器輸出u(t)波形,如圖2所示。 圖2 正弦激勵輸出波形 對輸出u(t)諧波線性化處理,得到其基波分量A1和B1: (2a) (2b) 可以看到當參數α*和β確定后,A1、B1與施加信號的頻率無關,即為頻率無關基波分量。因此,也稱其對應的非線性環節為簡單非線性環節。利用基波分量可得到2-SMC的負倒描述函數-1/N1(A): (3) 將-1/N1(A)繪制于復平面,如圖3所示。 圖3 -1/N1(A)曲線 -1/N1(A)曲線是始于原點的直線,并隨著參數A的增大而遠離原點,與實軸的夾角φ可表示為: (4) 結合圖3和式(4)可以看到,若(α*-1)+β(α*+1)>0,則-1/N1(A)曲線位于第二象限;若(α*-1)+β(α*+1)<0,則-1/N1(A)曲線位于第三象限;若(α*-1)+β(α*+1)=0,則-1/N1(A)曲線為實軸負半軸。因此通過調整參數α*和β,控制器2-SMC的負倒描述函數曲線可在-90°~-270°間旋轉,從而改變G(jω)與-1/N1(A)的交點。利用經典DF法分析閉環系統的穩定性和抖振特性,可使控制系統輸出量y(t)的抖振特性滿足期望性能。 在上一節利用經典DF法分析了簡單非線性環節所引入的抖振特性。然而也存在一些較復雜的非線性環節(如圖4所示),其描述函數N(A,ω)與施加信號的頻率有關,因而不再適用于經典DF法。在本節將針對N(A,ω)提出一種廣義DF法,以求取抖振的穩定性和抖振特性。 圖4 復雜非線性系統框圖 將圖4所示閉環系統的幅相頻率特性表示為1/[1+G(jω)N(A,ω)],在奈氏穩定判據的基礎上,提出基于數值計算的廣義DF法穩定判據: 步驟1:確定角頻率分析范圍0<ω≤ωup,ωup為分析的角頻率上限; 步驟2:判斷在角頻率分析范圍內是否存在抖振特性(An,ωn),使得Im[G(jωn)N(An,ωn)]=0與Re[G(jωn)N(An,ωn)]=-1同時成立(可能存在多個抖振特性); 步驟3: 若An,ωn滿足式(5)和式(6),則(An,ωn)為穩定的抖振點; (5) (6) 步驟4: 若An,ωn滿足式(7)和式(8),則(An,ωn)為穩定的抖振點; (7) (8) 步驟5: 否則(An,ωn)為非穩定的抖振點。 判斷抖振(An,ωn)的穩定性,關鍵是分析G(jω)N(A,ω)特性曲線與點(-1, j0)的位置關系。依據奈氏穩定判據,若當A>An,G(jω)N(A,ω)不包圍(-1, j0);當A 圖5(a) 穩定抖振的幅相頻率特性 圖5(b) 非穩定抖振的幅相頻率特性 接下來利用圖5解釋步驟3~步驟5:圖5(a)中,當A=1.6時,G(jω)N(A,ω)特性曲線與負實軸交于(-1, j0)點且斜率為正,滿足式(5),隨著A的增大(減小),特性曲線與負實軸交點向右(左)移動,滿足式(6),依據奈氏穩定判據,其對應的抖振是穩定的;圖5(b)中,當A=0.033時,特性曲線與負實軸交于(-1, j0)點且斜率為負,滿足式(7),隨著A的增大(減小),特性曲線與負實軸交點向右(左)移動,不滿足式(8),依據奈氏穩定判據,其對應的抖振是不穩定的。 在實際應用中,特性曲線以正斜率穿越(-1, j0)的情況較多,而以負斜率穿越的情況少見。 在第2節中只分析了系統輸出量y(t)的抖振特性,而在工程應用中同樣十分關注其它狀態變量的抖振特性。在本節將利用廣義DF法分析圖1中狀態變量x2(t)的抖振特性。 圖6 重組后的系統框圖 在圖1基礎上重新劃分線性和非線性環節,得到圖6所示框圖。可直觀地看到非線性環節N2包含滑模控制器和G1(s),因此,N2一定與施加信號的角頻率ω相關,只能利用廣義DF法來分析x2(t)的抖振特性。 接下來將計算N2的描述函數,在N2的輸入端施加信號Asin(ωt),可得到x1(t)、yM(t)、σ(t)和u(t)的波形。由頻率法可知,x1(t)與x2(t)應同為正弦信號而相位和幅度受G1(s)決定,因此可將x1(t)表示為式(9): x1(t)=A0(ω)Asin(ωt+θ0(ω)) (9) 其中A0(ω)和θ0(ω)為G1(s)的幅頻特性和相頻特性。于是計算N2的基波分量: (10a) (10b) 從而得到N2的描述函數N2(A,ω)=B1/A+jA1/A。最后借助廣義DF法,可求出狀態變量x2(t)的抖振特性。 設計如圖1所示控制系統,其中被控對象為G1(s)=1/(s+3),G2(s)=1/((s+1)(s+2)),二階滑模控制器為式(1)所示控制器。本節將進行兩項實驗:實驗一選取多組控制器參數α*和β,將y(t)的抖振仿真結果與經典DF法估算結果比較,以驗證控制參數α*、β與抖振特性的關系;實驗二將以狀態變量x2(t)為研究對象,通過計算復雜描述函數,運用廣義DF法估算其抖振特性,同時與仿真結果對比。 為分析參數α*和β對控制系統抖振特性的影響,設置三組控制器參數如表1所示。利用經典DF法估算輸出量y(t)的抖振特性并與Matlab仿真實驗結果對比。首先繪制被控對象G(s)幅相頻率特性曲線和控制器負倒描述函數-1/N1(A)曲線,如圖7所示。從圖7可看到2-SMC的負倒描述函數曲線-1/N1(A)隨著參數α*和β的減小而逆時針旋轉,并從第二象限旋轉到第三象限。隨著-1/N1(A)逆時針方向旋轉,-1/N1(A)與G(s)的交點向角頻率減小方向運動,因而y(t)的抖振角頻率減小、抖振幅度增大。圖8為三組控制參數對應的y(t)仿真響應曲線,并測量了各自的抖振特性。表1列出了三組控制器參數對應的抖振特性的估算和仿真結果,可看到y(t)抖振角頻率的理論估算與仿真實驗結果較吻合,而抖振幅度的估算值稍小于仿真實驗結果,這可能是由于DF法只分析基波分量,而造成了一定誤差。 圖7 描述函數分析 圖8 三組參數對應的y(t)響應曲線 因此得到N2的描述函數N2(A,ω)=B1/A+jA1/A,以及G2(jω)N2(A,ω)的表達式。當選定控制器參數α*=1.5,β=0.5,M=1時,利用廣義DF法并經過一系列代數運算和求導計算,可求得An=0.031,ωn=6.5 rad/s,且G2(jωn)N2(An,ωn)滿足廣義DF法步驟3的抖振穩定條件。 在仿真實驗中,利用Matlab仿真了圖6所示的控制系統,得到了x1(t)、x2(t)的仿真響應曲線如圖9(a)所示。繪制了以x1(t)-x2(t)為相平面的相軌跡如圖9(b)所示,可看到系統從初始狀態x1(0)=0.1,x2(0)=0出發,圍繞平衡點旋轉并趨近,最終穩定于一極限環運動。對x2(t)傅里葉分析,截取1 000點數據進行頻譜分析如圖10所示。由于x2(t)的響應為近似正弦曲線,因此含有多個頻譜分量。從圖10中可看到頻譜中有兩個峰值,分別對應角頻率6.274 rad/s和6.294 rad/s。從圖9、圖10可看到,仿真實驗所得x2(t)的抖振特性為An≈0.040,ωn≈6.3 rad/s。x2(t)抖振特性的廣義DF法計算結果與仿真實驗基本吻合,特別是角頻率的估計精度較高(誤差小于6%),印證了廣義DF法的正確性。 圖9(a) x1(t)、x2(t)響應曲線 利用經典和廣義DF法,研究了2-SMC可調參數影響系統抖振特性的機理,推導了系統輸出量和狀態變量抖振特性的估算方法,得到了系統抖振特性的調節方法。提出了廣義DF法以分析復雜非線性環節的抖振特性,給出了抖振的穩定條件,并利用廣義DF法估算了控制系統狀態變量的抖振特性。實驗數據對比表明,經典和廣義DF法對抖振角頻率的估算精度較高。該方法可指導滑模控制系統的設計,從而抑制系統抖振幅度、調節抖振頻率、避免系統共振。 [1]Billings S A, Tsang K M. Spectral analysis for non-linear systems, part Ι: parametric non-linear spectral analysis[J]. Mechanical Systems and Signal Processing, 1989, 3(4): 319-339. [2]禹見達, 陳政清, 王修勇等. 改進的 Bang-Bang控制算法的理論與試驗研究[J]. 振動與沖擊, 2010, 29(2): 60-63. YU Jian-da, CHEN Zheng-qing, WANG Xiu-yong, et al. Theoretical and experimental study on an improved Bang-Bang control algorithm[J]. Journal of Vibration and Shock, 2010, 29(2): 60-63. [3]Gao W B, Wang Y F, Homaifa A. Discrete-time variable structure control systems[J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122. [4]Lee H, Utkin V I. Chattering suppression methods in sliding mode control systems[J]. Annual Reviews in Control, 2007, 31(2):179-188. [5]Oliveira N M F, Kienitz K H, Misawa E A. A describing function approach to the design of robust limit-cycle controllers[J]. Nonlinear Dynamics, 2012, 67(1): 357-363. [6]Huang Y J, Wang Y J. Steady-state analysis for a class of sliding mode controlled systems using describing function method[J]. Nonlinear Dynamics, 2002, 30(3): 223-241. [7]Boiko I. Analysis of modes of oscillations in a relay feedback system[C]. Proceeding of the 2004 American Control Conference Boston, Massachusetts, June, 2004: 1253-1258. [8]Boiko I. Oscillations and transfer properties of relay feedback systems with time-delay linear plants[J]. Automatica, 2009, 45(12): 2897-2902. [9]Boiko I, Castellanos I, Fridman L. Analysis of response of second-order sliding mode control systems to exteral inputs[C]. Proceedings of the 2006 International Workshop on Variable Structure Systems Alghero, Italy, June, 2006:172-177. [10]Boiko I, Fridman L, Pisano A, et al. Analysis of chattering in systems with second order sliding modes[J]. IEEE Transactions on Automatic Control, 2007, 52(11): 2085-2102. [11]Bartolini G, Pisano A, Punta E, et al. A Survey of applications of second-order sliding mode control to mechanical systems[J]. International Journal of Control, 2003, 76(9): 755-770.2 輸出量y(t)抖振特性分析
3 廣義DF法推導
4 狀態變量抖振特性分析
5 數值仿真實驗
5.1 實驗一
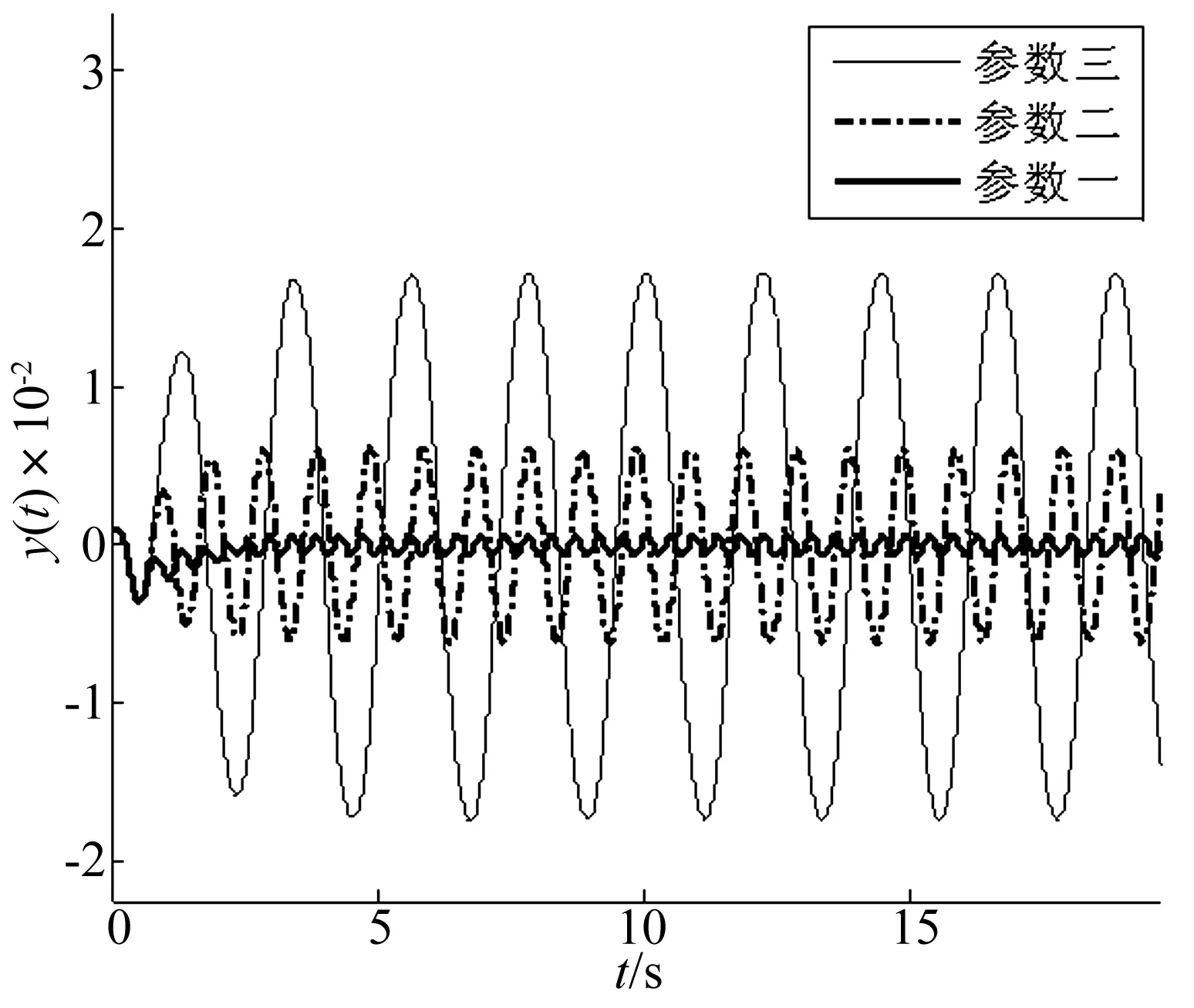
5.2 實驗二
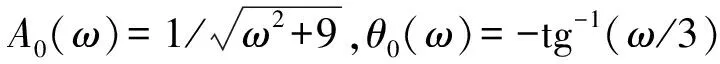
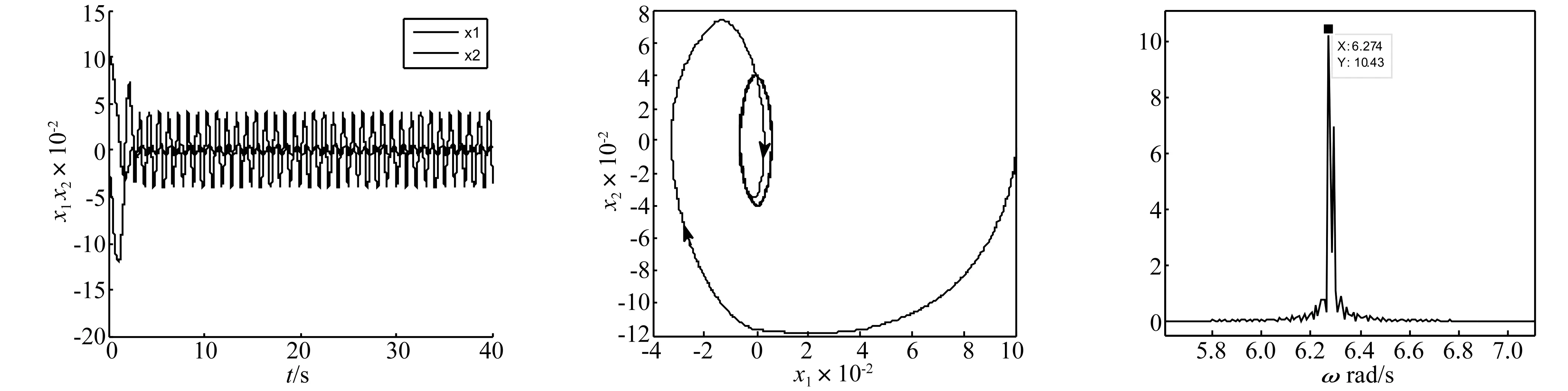
6 結 論

