環(huán)形密封對離心泵轉子系統(tǒng)穩(wěn)定性影響的數值研究

周文杰, 王樂勤, 邢桂坤, 翟璐璐 , 魏雪松 , 吳大轉

(1.浙江大學 化工機械研究所，杭州 310027； 2.中國寰球工程公司，北京 100029)

轉子-密封系統(tǒng)常見于農業(yè)灌溉的離心泵中。隨著轉速的不斷提高，離心泵轉子-密封系統(tǒng)將出現非線性特征，轉子密封處的自激力將對轉子系統(tǒng)產生很大影響，導致轉子的強烈振動甚至失穩(wěn)[1]。

對于轉子-密封系統(tǒng)的非線性和穩(wěn)定性研究，國內外學者已經做了許多相關研究工作，Muszynska等[2-4]在大量實驗和數據分析的基礎上引入了流體環(huán)向平均流速比，建立了非線性密封Muszynska模型，該模型已成為研究非線性密封的經典模型；Noah等[5]分析了線性密封模型的局限性并指出轉子系統(tǒng)考慮非線性密封模型的重要性；Ding等[6]采用Muszynska模型和Poore定性進行了轉子-密封系統(tǒng)穩(wěn)定性分析，但是只是針對完美平衡的對稱轉子-密封系統(tǒng)，具有一定的局限性；李松濤等[7-10]對迷宮密封等多種密封形式的轉子-密封系統(tǒng)進行了非線性動力穩(wěn)定性和分岔研究，拓展了非線性轉子-密封系統(tǒng)的密封結構，研究結果表明迷宮密封的參數對轉子-密封系統(tǒng)的振動和穩(wěn)定性有著十分重要的影響；薛麗輝等[11]得到了油膜力、氣流力和密封力三種非線性力作用下的高參數渦輪轉子復雜系統(tǒng)響應，但研究只是針對單跨對稱渦輪轉子的特別情況，而并非實際渦輪轉子；何立東等[12]建立了三維轉子密封流固耦合模型，通過直接對密封流場的非線性氣動力進行數值求解，得到了流固耦合效應的轉子密封氣流激振問題的分析方法，但對象只是簡單的轉子-密封系統(tǒng)，對于復雜的情況還需進一步研究；羅躍綱等[13]則建立了帶有裂紋故障的雙跨彈性轉子系統(tǒng)的動力學模型，研究了非線性油膜力下轉子系統(tǒng)周期運動的穩(wěn)定性及失穩(wěn)規(guī)律，結果表明在亞臨界轉速區(qū)和超臨界轉速區(qū)具有不同形式的倍頻及峰值。

本文通過將打靶法和Floquet理論相結合，對離心泵轉子-環(huán)形密封系統(tǒng)的非線性穩(wěn)定性及其分岔問題進行了研究，同時利用四階Runge-Kutta法對不同密封幾何參數情況下的離心泵轉子-密封系統(tǒng)進行數值求解，得到了密封參數對系統(tǒng)穩(wěn)定性的影響規(guī)律和離心泵轉子-密封系統(tǒng)在不同密封參數下的分岔圖、軸心軌跡、相圖和龐加萊映射，計算結果為離心泵轉子-密封系統(tǒng)的設計以及定性的控制轉子系統(tǒng)的穩(wěn)定性提供了理論依據。

1 轉子環(huán)形密封動力學模型

圖1左邊所示為離心泵轉子系統(tǒng)，考慮環(huán)形密封后轉子-密封系統(tǒng)可以簡化為右圖所示，轉子兩端簡支，環(huán)形密封位于圓盤軸向外側，其密封力等效作用于圓盤處，由于圓盤存在不平衡偏心量將產生渦動(圖中密封處為夸張表示)，圓盤質量為md，偏心距為e，圓盤轉子處的阻尼為Cd，剛度為Kd，轉子轉速為ω，密封力為Fx、Fy，g為重力加速度，x、y為與轉軸軸向垂直的橫向振動坐標，t為時間，系統(tǒng)動力學方程可以寫為：

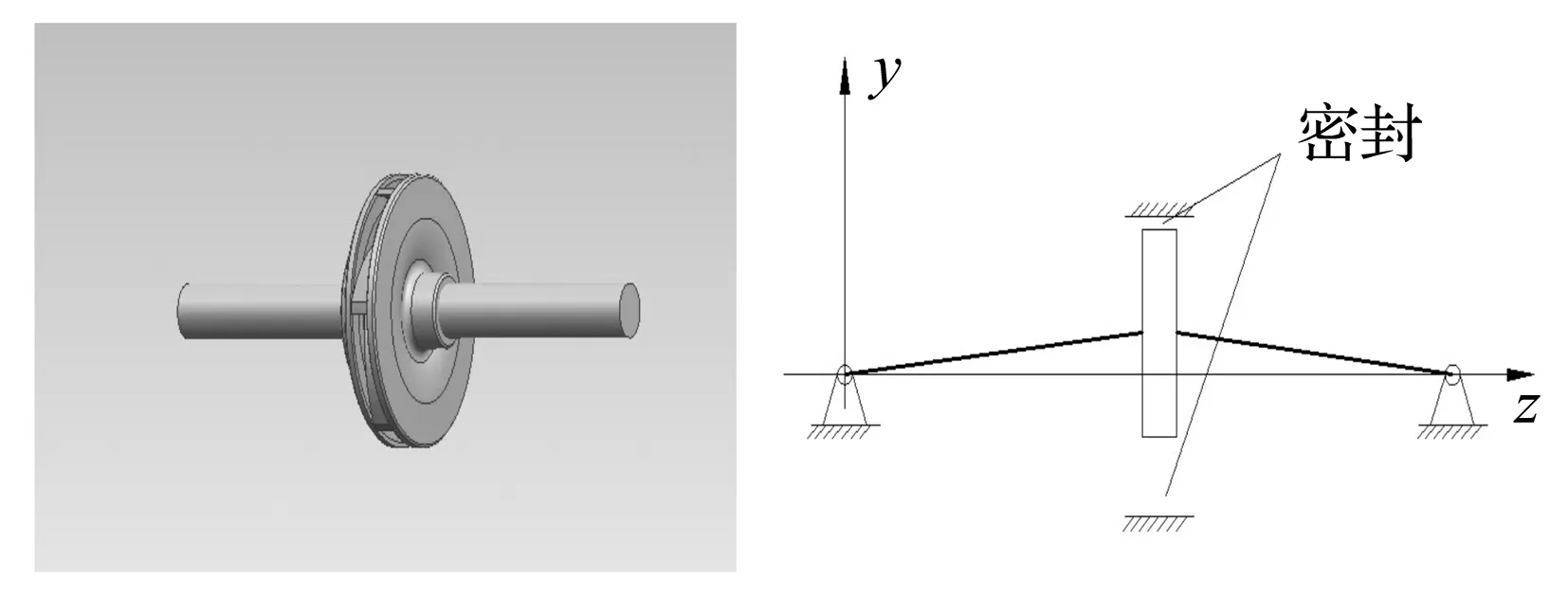
圖1 轉子-密封系統(tǒng)動力學模型

(1)

式(1)中密封力Fx、Fy采用非線性的Muszynska模型[3-4]，模型的特點是密封激振力對轉子的擾動反力以某固定角速度繞軸頸旋轉，其旋轉效應是誘發(fā)轉子失穩(wěn)的主要因素，該反力可以表述為：

(2)

實驗和數值研究結果證明式(2)中Ks、γ、Cs分別是密封剛度、密封流體周向平均速度與轉速的比值和密封阻尼，并且三者均是位移x、y的非線性函數，即

Ks=K0(1-ε2)-n1,

Cs=C0(1-ε2)-n1,n1=0.5～3

γ=γ0(1-ε2)n2,n2=0～1，γ0<0.5

式中:ε=(x2+y2)1/2/ξ為轉子相對偏心，ξ為密封間隙，K0、C0和ms三個動特性系數可以用Childs的環(huán)壓密封動力系數公式計算。

引入無量綱變換：

X=x/ξ,Y=y/ξ,t′=ωt

則等式(1)變?yōu)?/p>

(3)

式中：

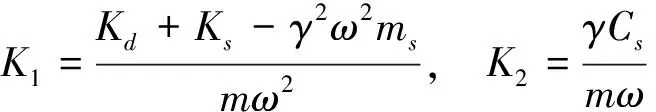
G=-mdg/(mω2ξ),ρ2=mde/(mξ)

將式(3)的二階方程轉化成一階方程，然后采用四階Runge-Kutta法對一階方程進行數值求解，即可得到轉子-密封系統(tǒng)瞬時響應。

2 Floquet理論

Floquet理論[14]是研究非線性動力系統(tǒng)穩(wěn)定性周期解分岔問題的一種方法。

對于一個給定的參數ω=Ω和對應的周期穩(wěn)態(tài)解X(t,Ω)=X(t+T,Ω)，其攝動方程可寫為：

(4)

這里A(t)=A(t+T)是一個周期為T的n×n矩陣函數，其具體形式為：

(5)

右邊非線性函數的Jacobi矩陣在周期穩(wěn)態(tài)解處的值，即：

(6)

由線性方程疊加原理，式(4)的任意n個線性獨立解為列的矩陣函數為其解矩陣：

Y(t)=[V1(t),V2(t),…,Vn(t)]∈Rn×Rn

(7)

式(4)的任意解都可以表示成：

V(t)=Y(t)BB={b1,b2,…,bn}T∈Rn

(8)

式中B是根據初始條件決定的常矢量。

由于Y(t)是式(4)的一個基解矩陣，則存在一個非奇異的T周期矩陣Φ(t)=Φ(t+T)和常數陣D，使：

Y(t)=Φ(t)exp(tD)

(9)

根據式(4)中A(t)的周期性特點，若Y(t)是式(4)的一個基解矩陣，則有：

A(t)Y(t+T)

(10)

由式(9)可得：

Y(t+T)=Φ(t+T)exp[(t+T)·D]=

Φ(t)exp(tD)exp(TD)=

Y(t)exp(TD)=Y(t)·C

式中C=exp(TD)為一常數陣。常數陣C與D的具體形式取決于Y(0)的選取，當然也與A(t)有關，定義矩陣C的特征值λ為Floquet乘子。

根據Floquet理論，當所有Floquet乘子的模都小于1時，系統(tǒng)是穩(wěn)定的；當一個Floquet乘子通過(-1,0)穿出單位圓，而其它乘子的模都小于1時，系統(tǒng)產生倍周期分岔；當一個Floquet乘子通過(+1,0)穿出單位圓，而其它乘子的模都小于1時，系統(tǒng)產生鞍結分岔；當一對共軛復Floquet乘子穿出單位圓，而其它乘子的模都小于1時，系統(tǒng)產生Hopf分岔。

3 打靶法

打靶法是求解非線性振動周期解問題的常用方法[15]，對于非線性周期解，實質上就是求解如下形式微分方程：

(11)

為求解式(11)，r為x函數的初值和終值的差值，引入待定參數矢量s，使其滿足邊界條件：

r(s)=x(0,s)-x(T,s)=0

x∈Rm,f∶R·Rm→Rn

(12)

此時式(11)可以寫成：

(13)

式中:x0、xT分別為t=0和t=T時解矢量的初值和終值，g(x)為方程與s有關的部分。

其次，要控制情緒，保持樂觀向上、不急不躁的心態(tài)。因為情緒激動可使腎上腺素分泌增加，內耳小動脈血管發(fā)生痙攣，內耳供氧不足導致突發(fā)性耳聾。

利用牛頓迭代法，將式(12)在第i次近似值si附近展開成泰勒級數，取其線性部分：

(14)

式中:Δsi=si-s(i+1)為參數矢量si的第i次修正量，而

(15)

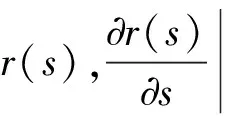
(16)

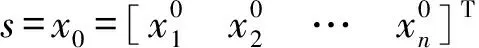
(17)

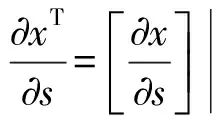
(18)

4 數值計算結果

初始密封基本參數和圓盤質量等其余參數如表1所示，分岔圖如圖2(a)所示，轉速為6 800左右時轉子—密封系統(tǒng)將產生Hopf分岔，系統(tǒng)將從穩(wěn)定狀態(tài)變成失穩(wěn)狀態(tài)。

表1 計算初始參數表

圖2 不同密封參數分岔圖

圖3(a)是轉速為2 000 r/min時的系統(tǒng)響應，從軸心軌跡可以看出，此時的轉子的渦動軌跡呈現橢圓形，在原點周圍穩(wěn)定運行，渦動量很小，并且龐加萊映射只存在一個獨立點，說明系統(tǒng)具有特定的周期，在圖4(a)的頻譜圖只有一個頻率；當轉速上升到8 000 r/min時，軸心軌跡將不再是橢圓，而變得十分復雜，渦動值與轉速較低時相比也增大了許多，并且開始變得發(fā)散，龐加萊映射由多個點集形成一個閉合曲線，說明此時轉子-密封系統(tǒng)已經由周期性穩(wěn)定運動變成了準周期運動，在圖4(b)的頻譜圖中也不再是單一頻率，出現了低頻的分頻，說明系統(tǒng)存在多個周期，也證明了此時系統(tǒng)是不穩(wěn)定的準周期運動。

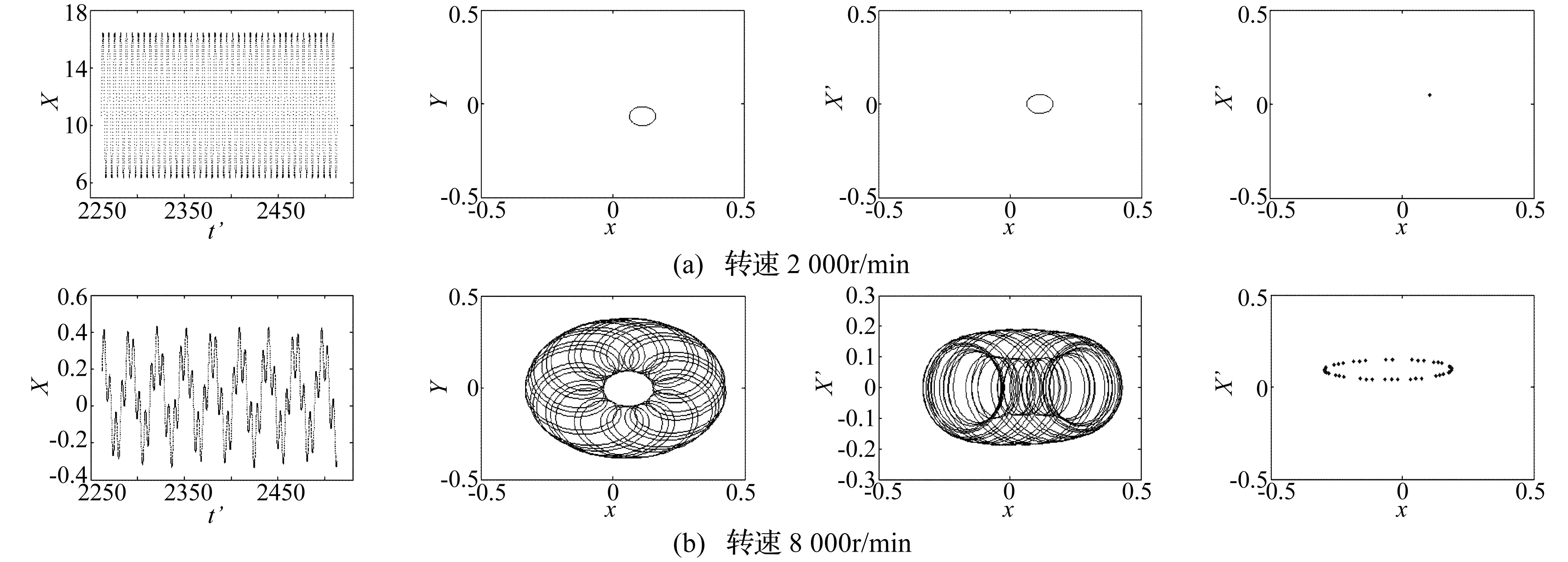
圖3 初始參數下不同轉速系統(tǒng)響應圖

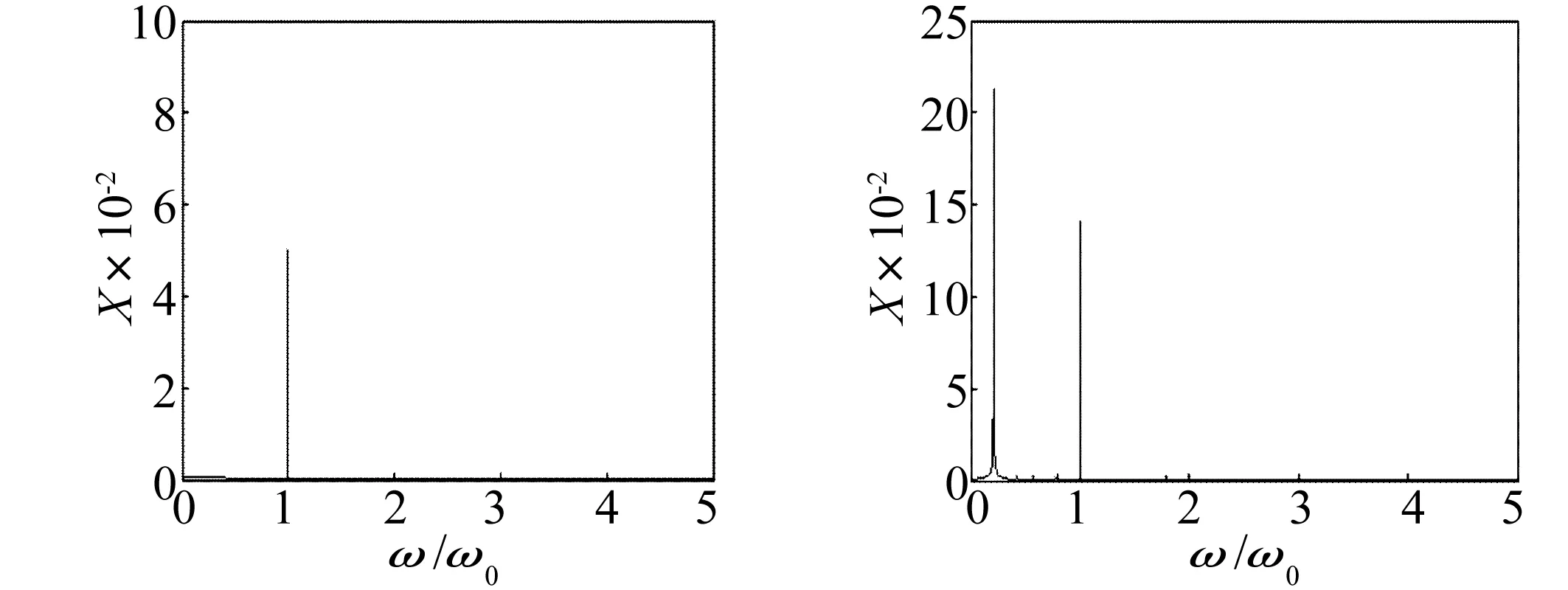
圖4 初始參數下不同轉速系統(tǒng)頻譜圖

改變環(huán)形密封兩邊壓差，將原先0.75 MPa增大至1.2 MPa，其余密封參數保持不變。由圖2(b)可知，壓差增大，轉子-密封系統(tǒng)產生Hopf分岔的失穩(wěn)轉速略有提高，說明適當增大壓差有利于離心泵轉子-密封系統(tǒng)的穩(wěn)定性。圖5可以看出，轉速為7 300 r/min時，系統(tǒng)由穩(wěn)定渦動運行逐漸變得不再穩(wěn)定，渦動幅值將逐漸變大，軸心軌跡呈現發(fā)散跡象，此時的龐加萊映射不是獨立的一點，而是多個點，并且有形成一閉合曲線的趨勢，說明轉速增大系統(tǒng)將進入準周期運動。

圖2(c)和圖2(d)分別為保持其余參數不變，增大密封間隙至0.001 2 m和增加密封長度至0.12 m時的分岔圖，由圖2(a)比較可知，增大密封間隙和密封長度將使失穩(wěn)轉速略有降低，降低轉子-密封系統(tǒng)的穩(wěn)定性，但相對增加壓差和增加密封長度而言，增大密封間隙對系統(tǒng)的穩(wěn)定性影響相對較小。圖6和圖7為增大密封間隙和增加密封長度的系統(tǒng)響應圖，在轉速為9 000 r/min時，由于轉速較快，系統(tǒng)失穩(wěn)呈現準周期運動，軸心軌跡以及相圖均是發(fā)散狀態(tài)，龐加萊映射為一閉合曲線。與初始狀態(tài)相比，此時的渦動幅值更大，若繼續(xù)提高轉速，轉子-密封系統(tǒng)將會與離心泵殼體發(fā)生碰摩事故。

圖5 壓差1.2 MPa轉速7 300 r/min系統(tǒng)響應圖

圖6 間隙0.001 2 m轉速9 000 r/min系統(tǒng)響應圖

圖7 長度0.12 m轉速9 000 r/min系統(tǒng)響應圖

表2為利用打靶法和Floquet理論計算得到的系統(tǒng)失穩(wěn)轉速時的Floquet乘子，在初始密封參數情況下系統(tǒng)失穩(wěn)轉速為6 680 r/min，增大密封壓差，增大密封間隙及增加密封長度時失穩(wěn)轉速將分別達到7 180 r/min,6 640 r/min和6 540 r/min，這與圖2利用四階Runge-Kutta法計算得到分岔圖中失穩(wěn)轉速基本是一致的。

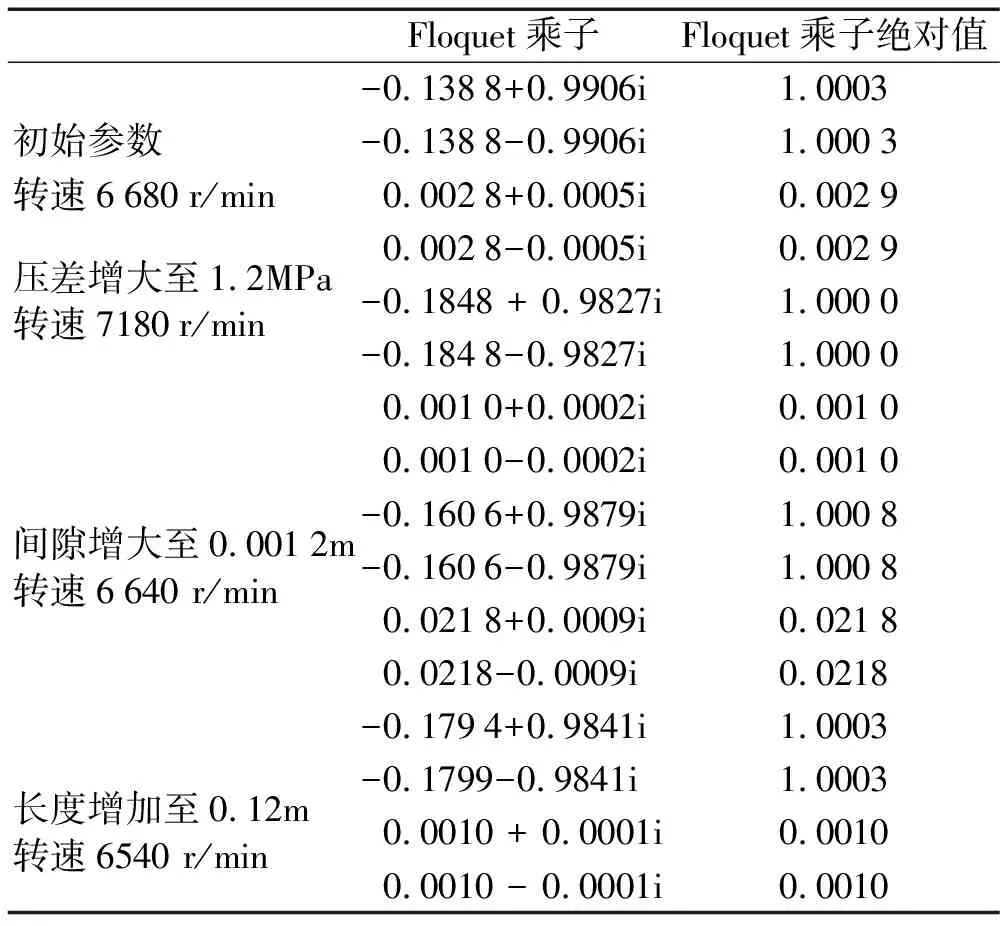
表2 失穩(wěn)轉速時的Floquet乘子

5 結 論

(1) 環(huán)形密封中的流體激勵力是離心泵轉子-密封系統(tǒng)失穩(wěn)的重要因素。在轉速較低時，轉子-密封系統(tǒng)呈現出穩(wěn)定的周期渦動，隨著轉速的增大，系統(tǒng)將出現Hopf分岔而失穩(wěn)。

(2) 采用非線性密封Muszynska模型建立了轉子-密封系統(tǒng)動力學模型，同時利用四階Runge-Kutta法對離心泵轉子-密封系統(tǒng)進行數值求解，并將打靶法和Floquet理論相結合，較準確的求解得到了不同密封參數下系統(tǒng)的失穩(wěn)轉速。

(3) 適當增大壓差、減小密封間隙和減小密封長度均會提高離心泵轉子-密封系統(tǒng)出現Hopf分岔的失穩(wěn)轉速，在離心泵轉子-密封系統(tǒng)的設計和失穩(wěn)控制中可以采用以上措施提高系統(tǒng)的可靠性和穩(wěn)定性。

[1]IWATSUBO T，SHENG B C. Evaluation of seal effects on the stability of rotating fluid machinery[J]. International Journal of Rotating Machinery, 1995, 2(2): 85-92.

[2]Muszynska A. Improvements in lightly loaded rotor/bearing and rotor/seal models[J]. Journal of Vibration Acoustics, Stress and Reliability in Design, 1988, 110(2): 129-136.

[3]Tam L T, Przekwas A J, Muszynska A, et al. Numerical and analytical study of fluid dynamic forces in seals and bearings [J]. Journal of Vibration Acoustics, Stress and Reliability in Design, 1988, 110(3): 315-325.

[4]Muszynska A, Bently D E. Frequency-swept rotating input perturbation techniques and identification of the fluid force models in rotor/bearing/seal systems and fluid handling machines [J]. Journal of Sound and Vibration. 1990, 143(1)：103-124.

[5]Noah S T, Sundararajan P. Significance of considering nonlineareffects in predicting the dynamic behavior of rotating machinery[J]. Journal of Vibration and Control, 1995, 1(4): 431-458.

[6]Ding Q, Cooper J E, Leung A Y T. Hopf bifurcation analysis of a rotor/seal system[J]. Journal of Sound and Vibration, 2002, 252(5): 817-833.

[7]李松濤，許慶余，萬方義. 迷宮密封轉子系統(tǒng)非線性動力穩(wěn)定性的研究[J]. 應用力學學報，2002，19(2)：27-30.

LI Song-tao, XU Qing-yu, WAN Fang-yi. A study on nonlinear dynamic stability of labyrinth seal-rotor system[J]. Chinese Journal of Applied Mechanics，2002，19(2)：27-30.

[8]Li S T, Xu Q Y, Zhang X L. Nonlinear dynamic behaviors of a rotor-labyrinth seal system[J]. Nonlinear Dynamics, 2007, 47(4): 321-329.

[9]劉思涌，薛自華，陸圯，等. 迷宮密封-轉子系統(tǒng)非線性動力學模型及求解[J]. 振動與沖擊，2012，31(13)：41-45.

LIU Si-yong, XUE Zi-hua, LU Yi, et al. Nonlinear dynamic model of labyrinth seal-rotor system and its solution[J]. Journal of Vibration and Shock, 2012, 31(13): 41-45.

[10]Wang W Z, Liu Y Z, Meng G, et al. Nonlinear analysis of orbital motion of a rotor subject to leakage air flow through an interlocking seal[J]. Journal of Fluids and Structures, 2009, 25(5): 751-765.

[11]薛麗輝，曹樹謙. 三種非線性力作用下高參數渦輪轉子復雜運動響應[J]. 工程力學，2011，28(7)：210-216.

XUE Li-hui, Cao Shu-qian. Complex response of a high-parameter turbo rotor model under three nonlinear forces[J]. Engineering Mechanics, 2011, 28(7): 210-216.

[12]何立東，高金吉，金琰，等. 三維轉子密封系統(tǒng)氣流激振的研究[J]. 機械工程學報，2003，39(3)：100-104.

HE Li-dong, GAO Jin-ji, JIN Yan, et al. Study on gas flow-induced vibration for a three-dimensional rotor-seal system[J]. Chinese Journal of Mechanical Engineering, 2003, 39(3): 100-104.

[13]羅躍綱，張松鶴，劉曉東，等. 含裂紋雙跨轉子一軸承系統(tǒng)周期運動的穩(wěn)定性[J]. 農業(yè)機械學報，2007，38(5)：168-172.

LUO Yue-gang, ZHANG Song-he, LIU Xiao-dong, et al. Stability of a two-span, rotor-bearing system with crack fault[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(5): 168-172.

[14]吳浩. 可傾瓦滑動軸承—轉子系統(tǒng)非線性動力學特性分析[D]. 哈爾濱：哈爾濱工業(yè)大學，2007.

[15]周紀卿，朱因遠. 非線性振動[M]. 西安：西安交通大學出版社，1998.