基于CHI-LMD方法的轉子振動信號分析
鄧林峰,趙榮珍
(1. 蘭州理工大學 機電工程學院,蘭州 730050;2. 蘭州理工大學 數字制造技術與應用省部共建教育部重點實驗室,蘭州 730050)
由于機械設備的振動信號往往包含豐富的故障特征信息且易于工程采集,所以在旋轉機械的狀態監測與故障診斷研究及應用中,利用振動信號進行分析是目前最主要的一種故障診斷方法[1-2]。然而,當機械設備發生質量不平衡、動靜碰摩等故障時,其轉子-軸承系統(Rotor-Bearing System, RBS)的剛度、阻尼和彈性力等都發生變化,RBS實際上成為一個時變的非線性系統,從而使振動信號表現出明顯的非平穩特性[1]。因此,如何從非平穩的振動信號當中提取故障特征,就成為機械故障診斷研究需要解決的關鍵問題[3]。
為了提取故障特征,國內外學者采用各種信號分析方法處理振動信號,使故障特征提取技術有了很大的進步[4-7]。由于非平穩信號具有時變特性,所以必須對其進行時頻聯合分析才可能獲得準確全面的特征信息,進而發現信號的瞬時變化特征[8]。因此,針對非平穩過程的時頻分析方法受到故障診斷研究特別多的關注[9]。其中,局部均值分解(Local Mean Decomposition, LMD)近年來格外引人矚目,尤其是國內學者,已經開展了大量關于將LMD方法應用到機械故障診斷中的研究工作,并取得了一些創新性的研究成果[10-13]。LMD與經驗模態分解(Empirical Mode Decomposition, EMD)相比,二者十分相似,都是一種自適應的信號分解方法,可以將一個多成分的復雜信號分解為若干個單分量的具有物理意義的簡單信號,再經過一系列的計算得到原始信號的時頻分布。但是,LMD無過包絡、欠包絡和Hilbert變換的負頻率等問題,端點效應也不如EMD明顯,因此基于LMD方法的故障診斷迅速成為一個研究熱點[14]。然而,LMD在計算局部均值函數和局部包絡函數時,需要利用滑動平均算法對局部均值和局部幅值進行平滑。研究[15-17]發現,平滑步長對于平滑過程和平滑結果有較大影響,若選擇不當,將形成比較明顯的計算誤差。
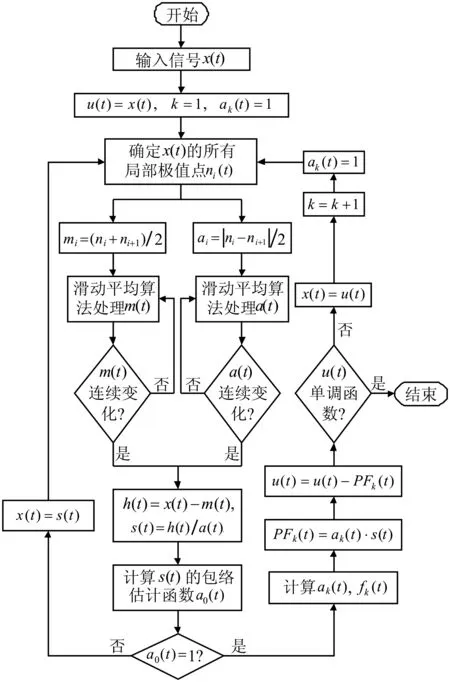
圖1 LMD算法流程圖
針對LMD方法在計算局部均值函數和局部包絡函數時的缺陷,文獻[15]提出了用三次樣條插值方法替換滑動平均過程的LMD改進算法,使LMD的計算效率和精度有了明顯提升,但與此同時,三次樣條插值的過包絡和欠包絡問題也被隨之引入,導致計算結果仍然存在一定的誤差。為減小三次樣條插值LMD算法的計算誤差,本研究利用分段三次Hermite插值方法計算信號的上/下包絡線,并將正交性準則作為乘積函數迭代運算過程是否結束的判斷依據,以進一步提高LMD算法的計算效率,最后通過仿真信號和實驗信號驗證了改進算法的有效性。
1 基于樣條插值的LMD方法
給定一個復雜信號x(t),則LMD對其進行分解的整個過程可以通過圖1所示的流程圖進行表示。信號x(t)經過圖1所示算法的處理,將得到一組PF分量PFk(t)及其瞬時頻率fk(t)和瞬時幅值ak(t),從而可構成x(t)的完整時頻分布。而分解后的x(t)則可表示為:
(1)
從圖1可見,LMD算法是一個具有三層循環結構的迭代過程。其中,最內層循環即為計算局部均值函數m(t)和局部包絡函數a(t)的迭代過程,這個循環實際上是通過滑動平均過程對所有相鄰極值點之間的局部均值和局部幅值進行反復平滑,而滑動平均算法對數據進行更新處理的計算公式為:
w(i+h)]
(2)
式中,w(i)為原數據,ws(i)為更新后的數據,2h+1表示滑動步長。現以五點法(2h+1=5)為例,則滑動平均算法的數據處理過程可描述如下:
(3)
式中:N為數據長度。按式(3)對數據列進行一次滑動平均之后,如果新的數據列{ws(i);i=1, 2,…,N}中還存在相鄰點相等的狀況,則將其作為原序列繼續循環實施滑動平均過程,直到任何相鄰的兩個數據點都不再相等為止[17]。
步長是滑動平均算法的一個重要參數,它直接影響平滑計算的結果。通常情況下,以最長局部均值的三分之一長度作為滑動步長[18],但由于非平穩信號的時變特性,分解結果并不理想。
由于LMD中的滑動平均算法在分解非平穩信號時存在分解精度和效率偏低的缺陷,文獻[15]將三次樣條插值法引入到LMD中,即利用數值插值方法替換滑動平均算法來計算局部均值函數和局部包絡函數,從而提高LMD算法的性能。通過這種替換,改進后的基于樣條插值的LMD算法為:
(1) 搜索到信號x(t)的所有局部極值點后,用極大值進行三次樣條插值,形成上包絡函數Eu(t);用極小值進行三次樣條插值,形成下包絡函數El(t)。
(2) 局部均值函數m(t)和局部包絡函數a(t)則用如下兩式分別進行計算:
(4)
(5)
(3) 接下來的步驟按照LMD算法的原過程步驟進行即可。
經過上述方式改進的LMD算法稱之為基于三次樣條插值(Cubic Spline Interpolation)的LMD(CSI-LMD)方法。由于CSI-LMD算法比圖1所示的LMD算法少了最內層的一個迭代過程,所以CSI-LMD的分解步驟變得相對簡單。盡管CSI-LMD算法在分解精度與計算效率上相比LMD算法都有所提高,但是利用三次樣條插值形成上/下包絡線,就不可避免地存在過包絡和欠包絡的問題,這將使得由式(4)和式(5)計算的局部均值函數和局部包絡函數也產生偏差而對最終分解結果的準確性造成影響。
由于三次樣條插值要保持連續的二階導數,插值函數的極值可能不出現在插值節點上,使得插值曲線的極值點偏移,反映到包絡線上,就形成了過包絡和欠包絡現象。與三次樣條插值相比,分段三次Hermite插值(Cubic Hermite Interpolation, CHI)也是采用三次多項式進行逼近,具有足夠的光滑性,但是它不需要保證二階連續導數,能夠保證兩個插值點間的擬合曲線是單調的,從而可以避免過包絡和欠包絡問題的產生。因此,本研究擬采用CHI對CSI-LMD算法進行二次改進以進一步提高其分解信號的性能。
2 分段Hermite插值方法
給定區間[a,b]上的一個劃分Δ,
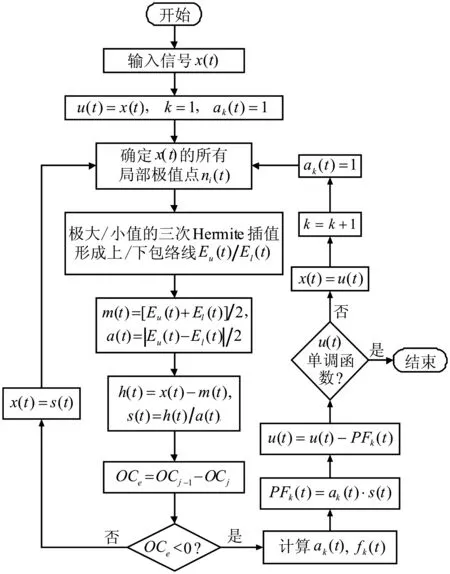
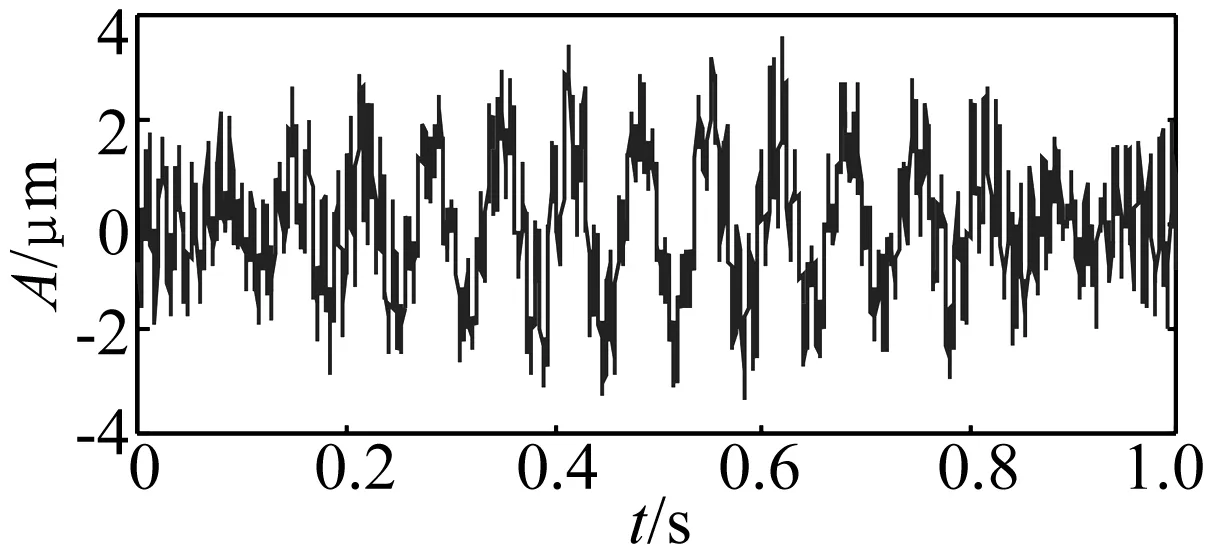
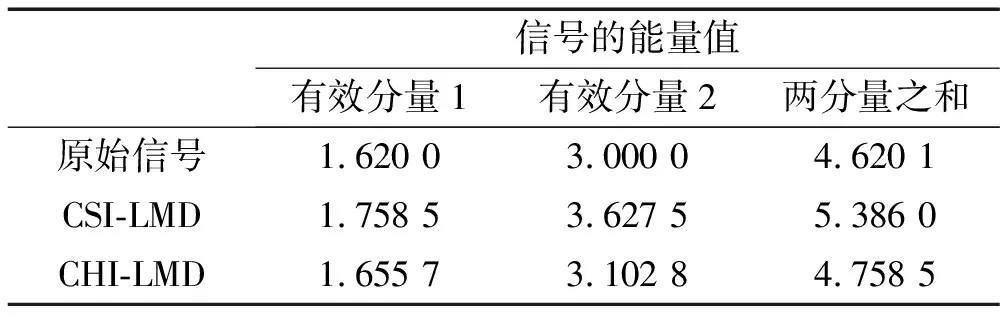
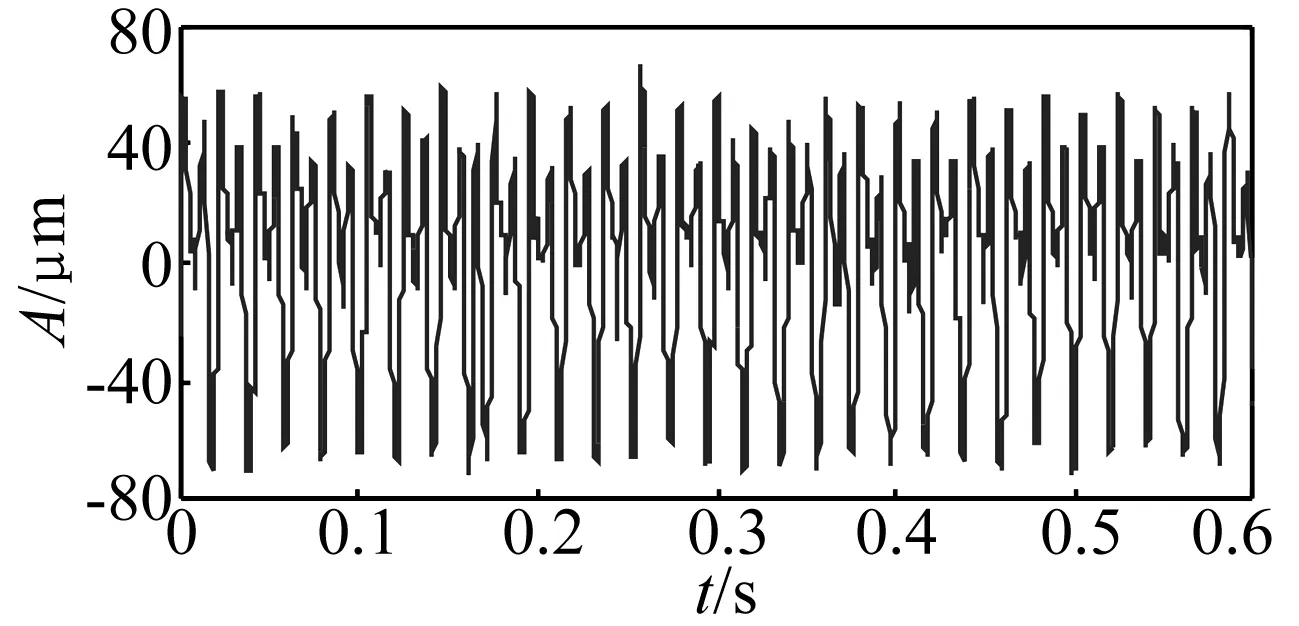
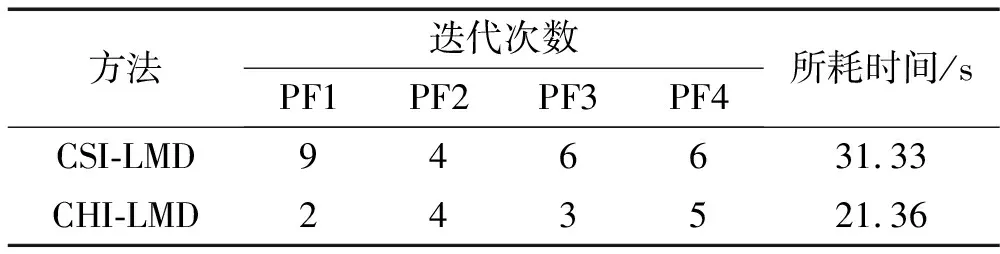
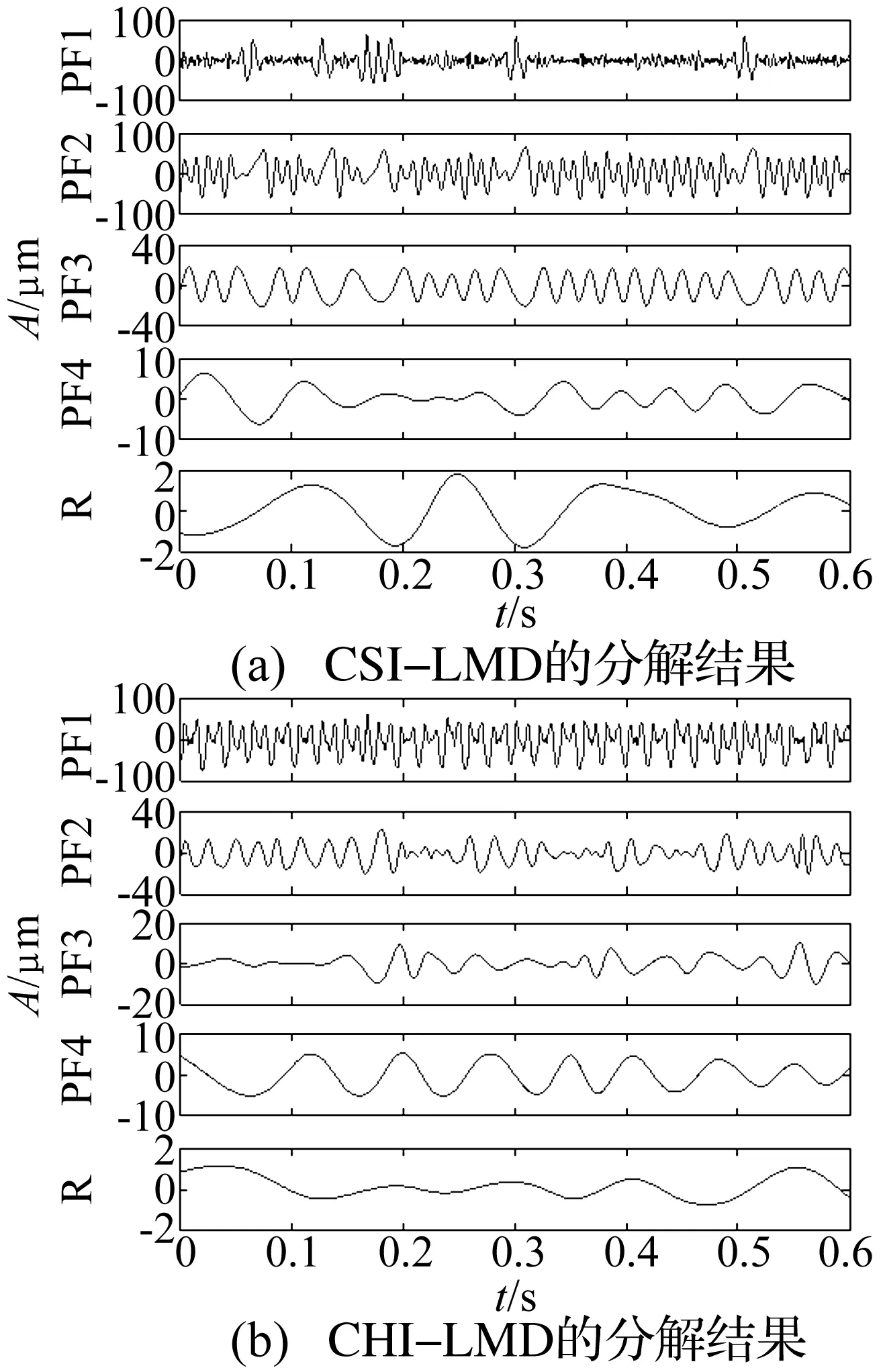
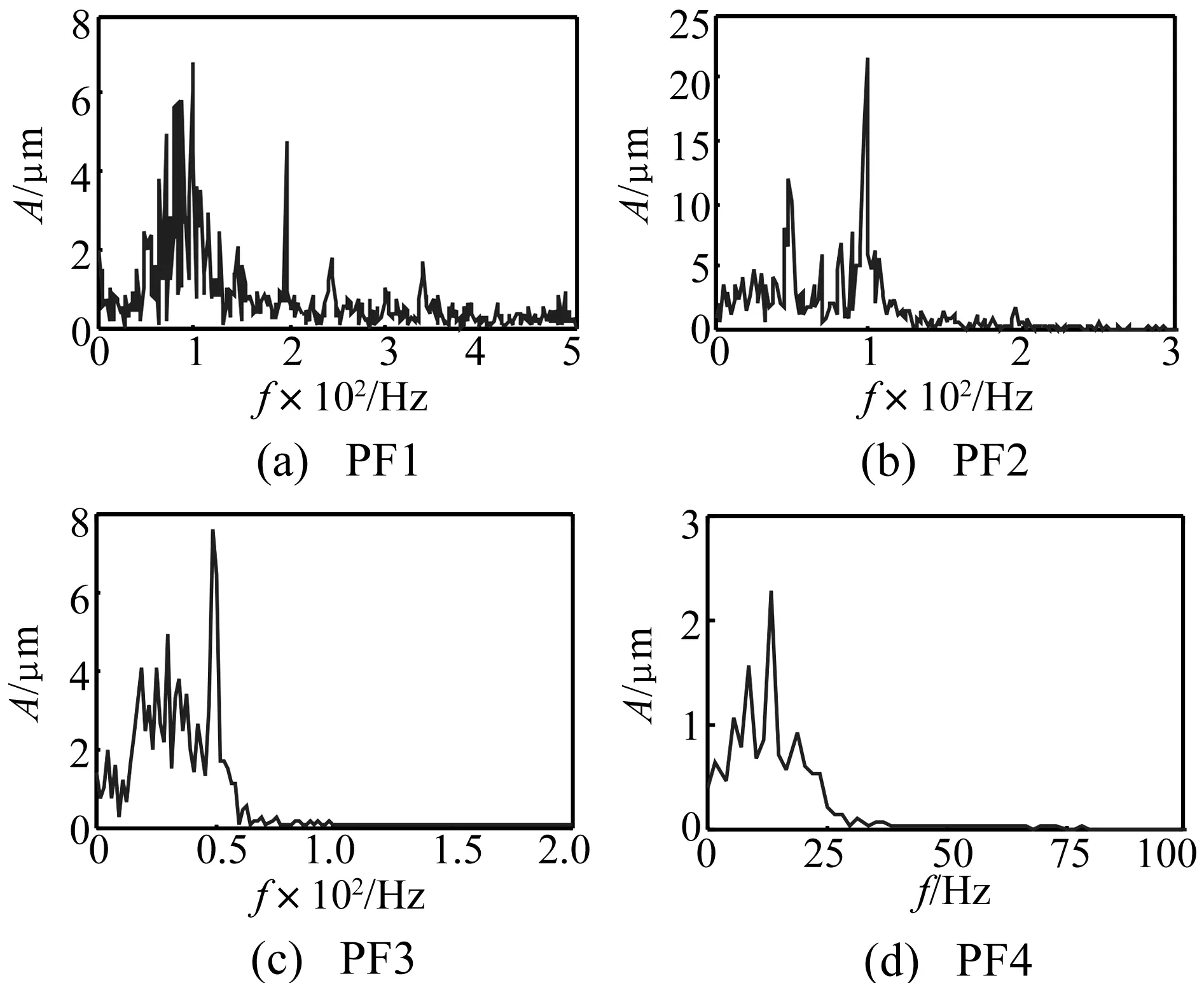
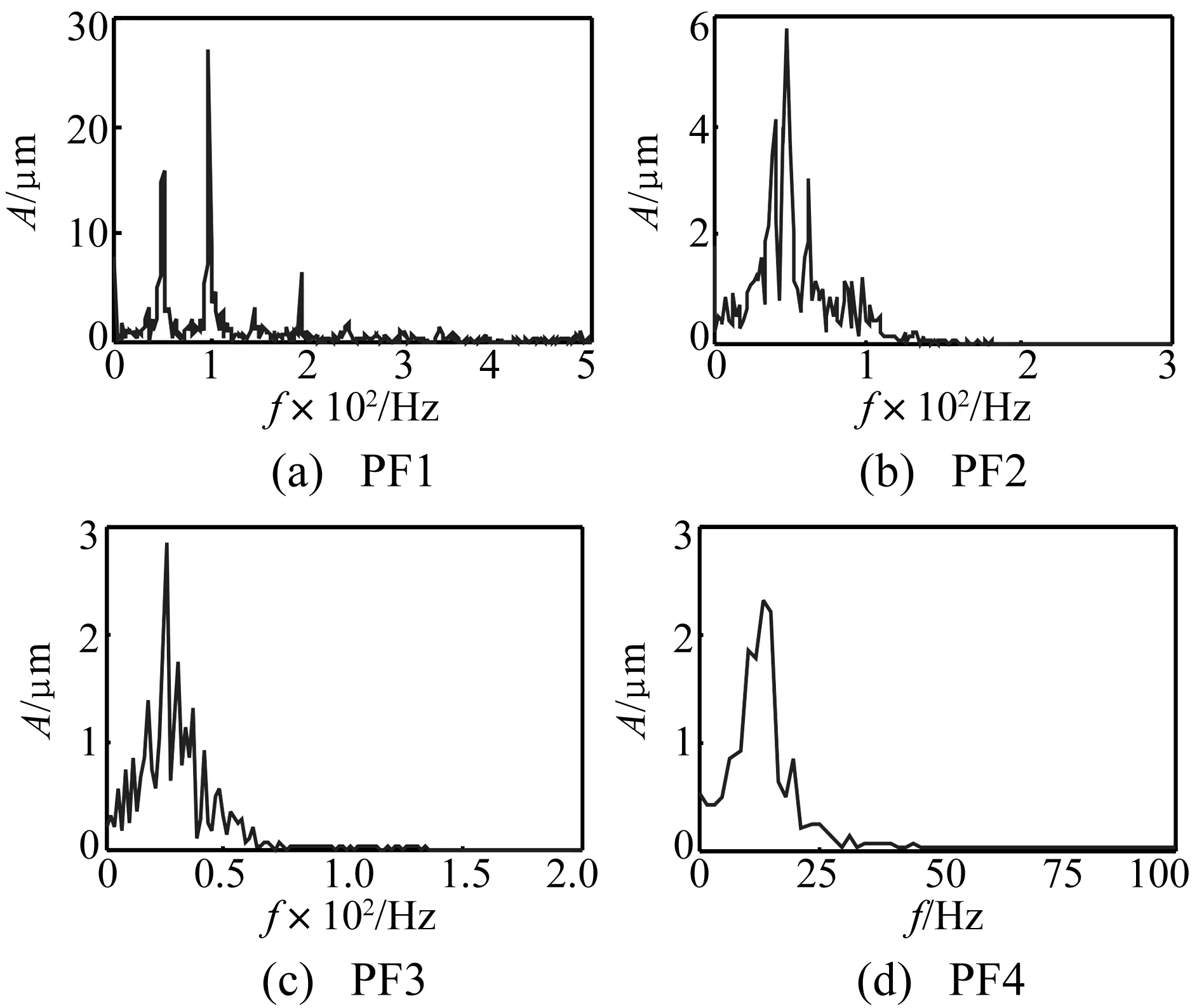
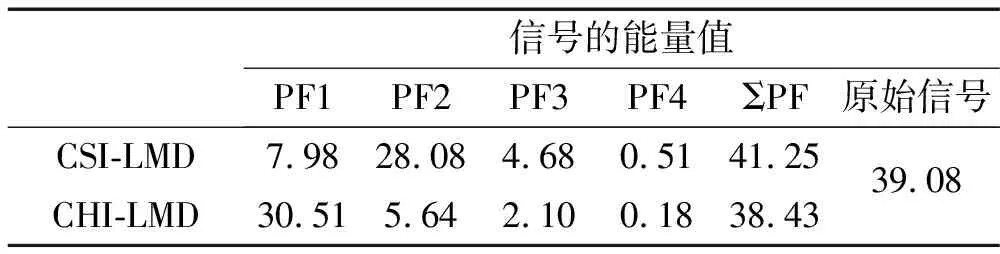
Δ∶a=x0 (6) i=0,1,…,n (7) 則稱 H(x)=Hi(x),x∈[xi-1,xi] i=1, 2,…,n (8) 是關于劃分Δ的分段三次Hermite插值函數,式(7)稱為插值條件。而由Lagrange法構造的分段三次Hermite插值多項式函數可表示為: x∈[xi-1,xi] (9) 式中:αk(x)和βk(x)稱為分段三次Hermite插值多項式的基函數,hi=xi-xi-1。 分段三次Hermite插值多項式具有公式簡單、計算量小、穩定性好、一致收斂等優點,與三次樣條插值方法一樣,每一個子區間上的三次Hermite插值多項式是整個插值函數不可缺少的一部分;而這些分段多項式的幾何表示是一些光滑的三次曲線,將它們拼接起來,便形成一條完整光滑的插值曲線。 三次樣條插值使CSI-LMD方法存在過包絡和欠包絡的問題,最終將導致信號分解的結果產生偏差。而利用分段三次Hermite插值計算信號的局部均值函數和局部包絡函數,能夠盡量減弱包絡線的過沖和欠沖現象,從而可以提高算法的分解精度。基于此,本研究提出一種分段三次Hermite插值的LMD(CHI-LMD)方法,其具體的算法步驟為: (1) 找到任意信號x(t)的所有局部極值,用極大值進行分段三次Hermite插值,形成上包絡線Eu(t);用極小值進行分段三次Hermite插值,形成下包絡線El(t)。 (2) 局部均值函數mi(t)和局部包絡函數ai(t)可以通過式(4)和式(5)計算得到。 (3) 接下來的步驟按照LMD算法的原過程步驟進行即可。 與CSI-LMD方法相比,以上算法步驟只是采用不同的插值方法,雖然克服了過/欠包絡問題,但是在實際的信號分解過程中,PF分量的迭代終止條件采用的仍然是局部包絡函數的幅值要小于給定的閾值,而這種判別方式也會使得分解結果產生誤差。由文獻[19]可知,LMD方法中的PF分量之間滿足正交性,即: i=1,2,…,k (10) 式中,k為PF分量的個數。式(10)說明每個PF分量都與將其從原始信號x(t)中分離出來的剩余部分正交。 理論上,每個PF分量都應該滿足式(10),但實際應用中,由于LMD方法的分解過程存在一定誤差,每個PF分量并不是嚴格的正交關系,所以,式(10)中的等號只能是在近似意義下成立;當然,等號左邊的值越接近0,說明PF分量的正交性越好,LMD的分解結果就越準確。 基于PF分量的以上性質,將正交性準則(Orthogo-nality criterion, OC)引入到CHI-LMD方法中,以進一步提高該方法的性能,從而能夠更準確有效地分析處理非平穩信號[19]。其中,正交性準則OC的定義如下: (11) 式中,x(t)為原始信號,mij(t)為LMD在求解第i個PF分量時計算的第j次局部均值函數。 由于式(11)是基于式(10)而建立起來的,因此它能夠很好地反映LMD分解過程的正交性。此外,由LMD的分解步驟可知,隨著迭代次數j不斷增加,mij(t)將趨向于0,從而式(11)中等號右邊的分子和分母將同時趨向于0,并且二者的收斂速度一致,即分子和分母是等價無窮小,所以OC的值將趨向于1,這與LMD方法理論上的迭代終止條件也是相一致的。因此,利用OC作為迭代終止條件不僅可以保證分解的正交性,而且能夠減少分解過程的迭代次數和時間,具有較快的收斂速度,從而提高了算法效率。但是,OC的值也只是趨近于1,而且,并不是隨著迭代次數的增加呈單調遞減的趨勢,即OC的值在到達最小的某一個值后,當分解過程繼續進行時,它反而開始增大或出現振蕩變化的情形。因此,OC極小值所對應的分解次數即為PF分量迭代過程的最佳迭代次數。基于此,以前后兩次相鄰迭代過程中OC的差值是否小于零作為PF分量的迭代過程結束的判別條件。 對CSI-LMD方法進行以上兩方面的改進后,就形成基于OC判據的CHI-LMD方法,該方法的算法流程圖如圖2所示。為便于描述,下文中均以CHI-LMD方法指代基于OC判據的CHI-LMD方法。 圖2與圖1相比,很明顯,CHI-LMD方法是一個僅有兩層循環結構的分解過程,而LMD方法則是一個具有三層循環結構的迭代過程,即CHI-LMD方法的算法結構相對簡單,能夠減少算法的運行時間,提高算法的運行效率。此外,CHI-LMD算法以OC差值判斷法代替閾值判斷法決定產生PF分量的循環迭代過程是否應該結束,從而使分解得到的PF分量之間保持較好的正交性,以提高CHI-LMD方法的分解精度,并最終形成一種性能提升的CHI-LMD方法。 圖2 CHI-LMD算法流程圖 為驗證本文方法的有效性,通過仿真信號和轉子實驗信號對CSI-LMD和CHI-LMD方法的性能進行了分析比較。 構造一個仿真信號x(t): x(t)=x1(t)+x2(t)+n(t)= [1+0.4cos(10πt)]cos[160πt+2cos(16πt)]+ 2sin(πt)sin(30πt)+n(t) t∈[0,1] (12) 式(12)是由兩個不同的調頻-調幅分量x1(t)、x2(t)以及一個均值為0、方差為0.1的高斯白噪聲n(t)組成的非平穩信號,x(t)的時域波形如圖3所示。 圖3 仿真信號波形 分別采用CSI-LMD和CHI-LMD方法對x(t)進行處理,對于CSI-LMD方法,純調頻信號的迭代終止條件設定為,max[|1-ai(t)|]=0.01。x(t)經兩種方法分解后的結果如圖4所示。 圖4 信號x(t)的分解結果 從圖4可見,CSI-LMD和CHI-LMD方法都可以將x(t)分解為3個PF分量和1個剩余分量R。其中,PF1包含著主要的噪聲成分;PF2、PF3則分別對應有效分量x1(t)、x2(t)。此外,兩種方法的分解結果也存在明顯的差別,由CSI-LMD方法分解得到的PF2、PF3都出現了較為明顯的扭曲和失真,而由CHI-LMD方法分解出的PF2、PF3的誤差則相對較小。由此可見,CHI-LMD方法的分解精度比CSI-LMD方法的分解精度要高。 為驗證CHI-LMD方法采用OC判據的有效性,引入正交性指標(Index of orthogonality,IO)對分解結果的正交性進行評價,其定義如下[20]: i≠j (13) 式中,T為信號長度,k+1為PF分量的個數,第k+1個PF分量指剩余分量R。由式(13)可知,PF分量之間的正交性越好,則IO指標越接近于0。經計算,圖4所示兩個分解結果的IO指標分別為IOa=0.1329、IOb=0.031 0,由此可見,CHI-LMD方法的正交性更好。同時,計算了x(t)中有效分量x1(t)、x2(t)以及用兩種LMD方法分解得到的PF2、PF3的能量,結果如表1所示。從表1中的數據可見,由兩種方法分解出的有效分量PF2、PF3的能量都與原始信號的有效分量x1(t)、x2(t)的能量之間存在一定誤差,但是,利用CHI-LMD方法分解得到的PF分量的能量誤差較小,更接近實際信號的能量值,這些結果也說明CHI-LMD方法具有更高的分解精度。 表1 有效分量的能量對比 從圖5所示設置有輕微碰摩故障的轉子實驗臺上采集振動位移信號,采樣頻率為5 000 Hz,采樣點數為3 000。圖6是轉子轉速為3 000 r/min時,原始振動信號經過文獻[21]中的消噪方法處理后的時域波形。 圖5 轉子實驗臺照片 分別采用CSI-LMD和CHI-LMD方法對圖6所示的振動信號進行分解,兩種方法都得到了4個PF分量和1個余量R,分解結果如圖7所示。從圖中可見,兩種分解方法產生的PF分量存在一些差別,這是因為它們采用不同的方式計算局部均值函數和包絡估計函數,并使用不同的循環迭代條件。而在分解過程中,兩種方法產生每個PF分量所需要的迭代次數,以及整個分解過程所消耗的時間,如表2所示。 圖6 3 000 r/min時的碰摩振動信號 表2 分解過程的迭代次數和耗時 圖7 3 000 r/min碰摩振動信號的分解結果 表2中的數據顯示,CSI-LMD方法產生每個PF分量所需要的迭代次數都不少于CHI-LMD方法所對應的迭代次數,尤其對于分量PF1而言,前者是后者的4.5倍;而兩種分解過程所消耗的時間也存在明顯差距,接近于10 s。由此可見,CHI-LMD方法的效率更高。 盡管圖7中的PF分量表征了從高頻到低頻的幾個自然振動模式,但是無法給出明顯的故障特征,因此對其進行頻譜分析,結果如圖8、圖9所示。 從頻譜圖可見,由兩種LMD方法得到的4個PF分量都包含了頻率由高到低的主要振動成分。但是,兩種LMD方法分解出的PF分量的頻譜分布圖也存在一些明顯的差別。相比之下,由CHI-LMD方法分解得到的PF分量的頻譜分布圖,更準確地提取出了碰摩故障所引起的1/2、1及2倍頻等幾種特征成分[14]。 圖8 CSI-LMD的4個PF分量的頻譜 圖9 CHI-LMD的4個PF分量的頻譜 與仿真信號一樣,計算了兩種LMD方法的正交性指標IOa=0.076 5、IOb=0.036 7,而各PF分量的能量及能量和見表3。IO值的不同、表3中PF分量的能量和與原始信號能量之間的誤差大小則表明,CHI-LMD方法能夠更加準確地分解故障振動信號。 表3 信號分解后的能量對比 從以上結果可見,無論是分解過程的迭代次數與時間消耗,還是PF分量之間的正交性、PF分量的能量和與原始信號能量之間的誤差大小,以及提取故障轉子的特征振動成分等性能指標,CHI-LMD方法都具有一定的優勢,即CHI-LMD方法在計算效率和分解精度兩方面都優于CSI-LMD方法。 LMD是一種自適應的信號分解方法,特別適合于非平穩信號的時頻分析。本研究經過對CSI-LMD方法的插值方式和迭代判別條件進行改進,得到了一種基于OC判據的CHI-LMD方法,通過仿真信號和實驗信號的驗證,得出以下主要結論: (1) 相對于CSI-LMD方法,CHI-LMD方法在處理非平穩信號時,分解過程的迭代次數和時間消耗都較少,而且最終分解結果的誤差也較小。 (2) CSI-LMD與CHI-LMD方法相比,由后者分解得到的PF分量之間的正交性更好。 (3) CHI-LMD比CSI-LMD方法能夠更加準確地從故障信號當中分離出代表故障特征的振動成分。 [1]何正嘉, 訾艷陽, 孟慶豐, 等. 機械設備非平穩信號的故障診斷原理及應用[M]. 北京: 高等敎育出版社, 2001: 1-7. [2]De Moura E P, Souto C R, Silva A A, et al. Evaluation of principal component analysis and neural network performance for bearing fault diagnosis from vibration signal processed by RS and DF analyses[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1765-1772. [3]Muralidharan V, Sugumaran V. Feature extraction using wavelets and classification through decision tree algorithm for fault diagnosis of mono-block centrifugal pump[J]. Measurement, 2013, 46(1): 353-359. [4]Widodo A, Yang B S. Support vector machine in machine condition monitoring and fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2560-2574. [5]Cheng Jun-sheng, Yu De-jie, Yang Yu. The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 668-677. [6]Lei Y G, Zuo M J, He Z J, et al. A multidimensional hybrid intelligent method for gear fault diagnosis[J]. Expert Systems with Applications, 2010, 37(2): 1419-1430. [7]Wang Y X, Liang M. Identification of multiple transient faults based on the adaptive spectral kurtosis method[J]. Journal of Sound and Vibration, 2012, 331(2): 470-486. [8]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. [9]Feng Z P, Liang M, Chu F L. Recent advances in time frequency analysis methods for machinery fault diagnosis: A review with application examples [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 165-205. [10]Yang Yu, Cheng Jun-sheng, Zhang Kang. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J]. Measurement, 2012, 45(3): 561-570. [11]Wang Yan-xue, He Zheng-jia, Xiang Jia-wei, et al. Application of local mean decomposition to the surveillance and diagnostics of low-speed helical gearbox[J]. Mechanism and machine theory, 2012, 47: 62-73. [12]Zhang Yuan, Qin Yong, Xing Zong-yi, et al. Roller bearing safety region estimation and state identification based on LMD-PCA-LSSVM[J]. Measurement, 2013, 46(3): 1315-1324. [13]孫偉, 熊邦書, 黃建萍, 等. 小波包降噪與LMD相結合的滾動軸承故障診斷方法[J]. 振動與沖擊, 2012, 31(18): 153-156. SUN Wei, XIONG Bang-shu, HUANG Jian-ping, et al. Fault diagnosis of a rolling bearing using Wavelet packet de-noising and LMD[J]. Journal of Vibration and Shock, 2012, 31(18): 153-156. [14]Wang Yan-xue, He Zheng-jia, Zi Yan-yang. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis[J]. Journal of vibration and acoustics, 2010, 132(2): 0210101-02101010. [15]胡勁松, 楊世錫, 任達千. 基于樣條的振動信號局域均值分解方法[J]. 數據采集與處理, 2009, 24(1): 78-83. HU Jin-song, YANG Shi-xi, REN Da-qian. Spline-based local mean decomposition method for vibration signal[J]. Journal of Data Acquisition & Processing, 2009, 24(1): 78-83. [16]程軍圣, 張亢, 楊宇, 等. 局部均值分解與經驗模式分解的對比研究[J]. 振動與沖擊, 2009, 28(5): 13-16. CHENG Jun-sheng, ZHANG Kang, YANG Yu, et al. Comparison between the methods of local mean decomposition and empirical mode decomposition[J]. Journal of Vibration and Shock, 2009, 28(5): 13-16. [17]任達千. 基于局域均值分解的旋轉機械故障特征提取方法及系統研究[D]. 杭州: 浙江大學, 2008. [18]Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454. [19]張亢, 程軍圣, 楊宇. 局部均值分解方法中乘積函數判據問題研究[J]. 振動與沖擊, 2011, 30(9): 84-88. ZHANG Kang, CHENG Jun-sheng, YANG Yu. Product function criterion in local mean decomposition method[J]. Journal of Vibration and Shock, 2011, 30(9): 84-88. [20]Loutridis S J. Damage detection in gear systems using empirical mode decomposition[J]. Engineering Structures, 2004, 26(12): 1833-1841. [21]鄧林峰, 趙榮珍, 龔俊. 一種改進的轉子振動信號消噪方法研究[J]. 儀器儀表學報, 2011, 32(9): 1961-1966. DENG Lin-feng, ZHAO Rong-zhen, GONG Jun. Research on an improved de-noising method for rotor vibration signals[J]. Chinese Journal of Scientific Instrument, 2011, 32(9): 1961-1966.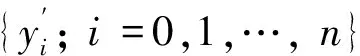
3 CHI-LMD改進方法
4 仿真分析和實驗驗證
4.1 仿真分析

4.2 轉子碰摩故障振動分析

5 結 論

