單面遮擋下受限甲烷氣云爆炸超壓模型研究

呂 東, 張 欣, 吳 偉, 李 晉

(公安部天津消防研究所, 天津 300381)

石油、石化、化工，以及家庭、賓館、小店鋪等多種行業、多種場所均存在可燃氣體爆炸風險。可燃氣體爆炸給人們帶來巨大的危害[1]。小體積可燃氣體爆炸在沒有遮擋的情況下，爆炸壓力一般只有幾千帕，不會引發災害；但是當可燃氣體體積增大，或者氣體爆炸遇到遮擋時，爆炸壓力會增大許多。如半球體無約束乙炔氣云半徑到達7.7 m時，無遮擋氣體爆炸超壓到達12 kPa，這個爆炸超壓足以引發玻璃窗破裂；當半球體氣云半徑到達23.7 m時，可使磚墻發生破壞[2]。遮擋的增強同樣會增強氣體爆炸壓力，如楊國剛[3]發現，對于半徑0.5 m的乙炔氣云，當遮擋物0.02 mm的聚乙烯膜從1層變4層時爆炸壓力從2.410 kPa增至13.125 kPa。在真實環境中,氣體爆炸范圍內往往會遇到各種障礙，有些障礙會增大氣體爆炸超壓，往往會發生大的災難。如2011年11月14日西安一個小吃店發生液化氣泄漏爆炸事故，造成7死31傷的嚴重事故。

對可燃氣體爆炸狀況進行建模研究，是減少其爆炸事故的重要組成部分。氣體爆炸模型有多種，如TNT當量法、TNO-MultiEnergy法和Baker-Strehlow法等。基于工程爆炸的TNT當量法常被用于氣體爆炸傷害計算[4-5]，但是TNT當量法來源于TNT炸藥爆炸經驗，與氣體爆炸情況存在一定的偏差。TNO-MultiEnergy法[6-9]和Baker-Strehlow[10-11]法自從上世紀80年代提出以來，經過多年的發展，在模擬氣體爆炸方面獲得了較多的應用。但是這兩個模型都未考慮遮擋對氣體爆炸的影響，只是粗略涉及到氣體的封閉狀況，至于如何封閉、多遠距離封閉等，均未在考慮之列。

由于在一些實際場景中涉及遮擋情形，研究遮擋對于爆炸超壓的影響，對于裝置布局、防爆設施設計、人員安全防護等極為重要。本文以計算流體力學為基礎，研究了單面遮擋對不同量級的甲烷氣體爆炸超壓帶來的影響，分析了爆炸超壓、氣體燃燒熱及距爆炸氣云中心的距離三點之間的關系，并建立了數學模型[12]。計算結果對甲烷氣體爆炸方面工程計算、實驗設計等均有一定的參考意義。

1 模型建立及監控分布

厚度為1 m的內部空間為3 m×3 m×3 m的建筑體封閉甲烷-空氣云團，建筑一側開口，開口位于墻面中心處，開口底端與地面等高，尺度為1 m×2 m。在距離開口處1 m遠處設置遮擋墻，寬度為5 m，高3 m，厚度1 m，如圖1所示。

圖1 幾何模型圖及部分超壓監測點

甲烷-空氣氣體云團設置為立方體，位于封閉建筑中心。氣體云團共分為5種，邊長分別為1 m，1.5 m，2 m，2.5 m和3 m。點火點位于氣團中心。

為了測得氣云爆炸引起的爆炸超壓，在如表1所示的位置設定爆炸超壓監測點。橫坐標從開口端氣體邊緣一直監測到距離云團中心24.5 m處；所有監測點的y坐標設定在建筑開口中心線上；由于人的耳膜、眼睛容易在爆炸超壓下引發損傷，綜合男女考慮，這些易受傷害的器官距離地面高度可以大約估計為1.6 m，因此將監測點的高度(z坐標)設計為1.6 m。

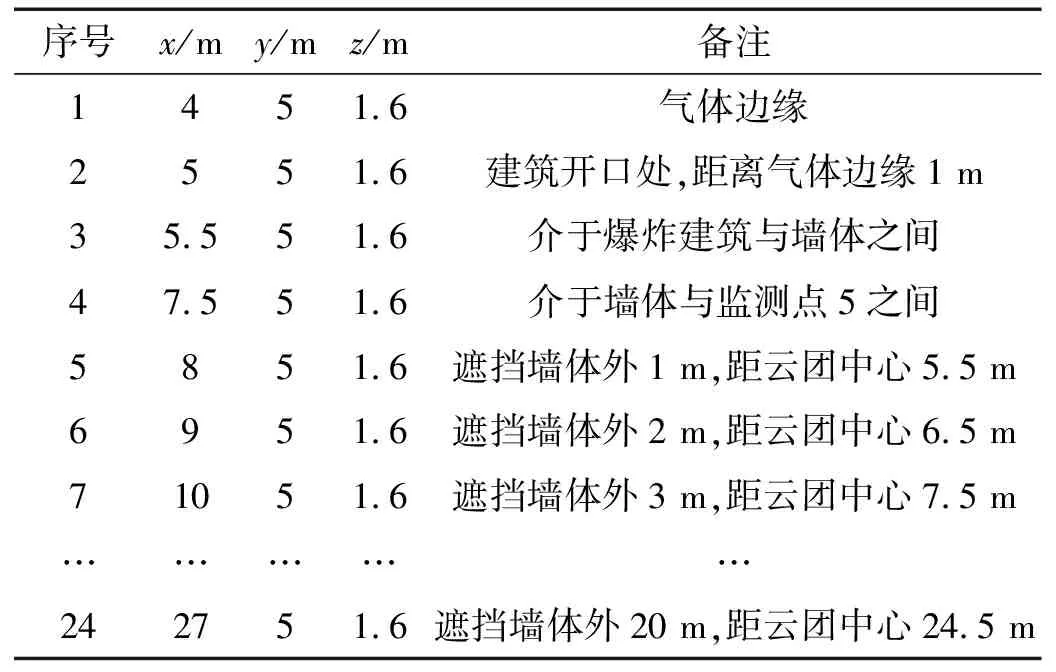
表1 甲烷氣云爆炸超壓監測點

2 模型計算

使用計算流體力學軟件FLACS進行模擬計算。FLACS使用有限體積法解決3維笛卡爾網格中質量、動量、能量等守恒問題。FLACS處理湍流的產生和消散采用的是標準k-ε模型[13]，它的建模過長經過了大量的試驗修正，使獲得模擬值接近真實爆炸數值。目前被國內外多家公司用于進行海洋平臺、陸上石油化工廠的通風、氣體泄漏、擴散和爆炸等方面的仿真計算分析。

假設爆炸時在無風的情況下進行，溫度為20 ℃，大氣壓為1 bar(100 kPa)，邊界條件設置為歐拉邊界。設置計算范圍為40 m×20 m×5 m。設置邊長為10 cm的正方體網格，將整個計算范圍分為400×200×50即4000000個單元格。爆炸介質為甲烷，其爆炸極限為5%-14.8%。本文設置甲烷與空氣當量比混合，為1∶9.5，甲烷的體積濃度約為9.5%。

經計算得知不同體積當量比混合的甲烷-空氣氣云在不同距離處發生爆炸得到的最大超壓，如表2所示。

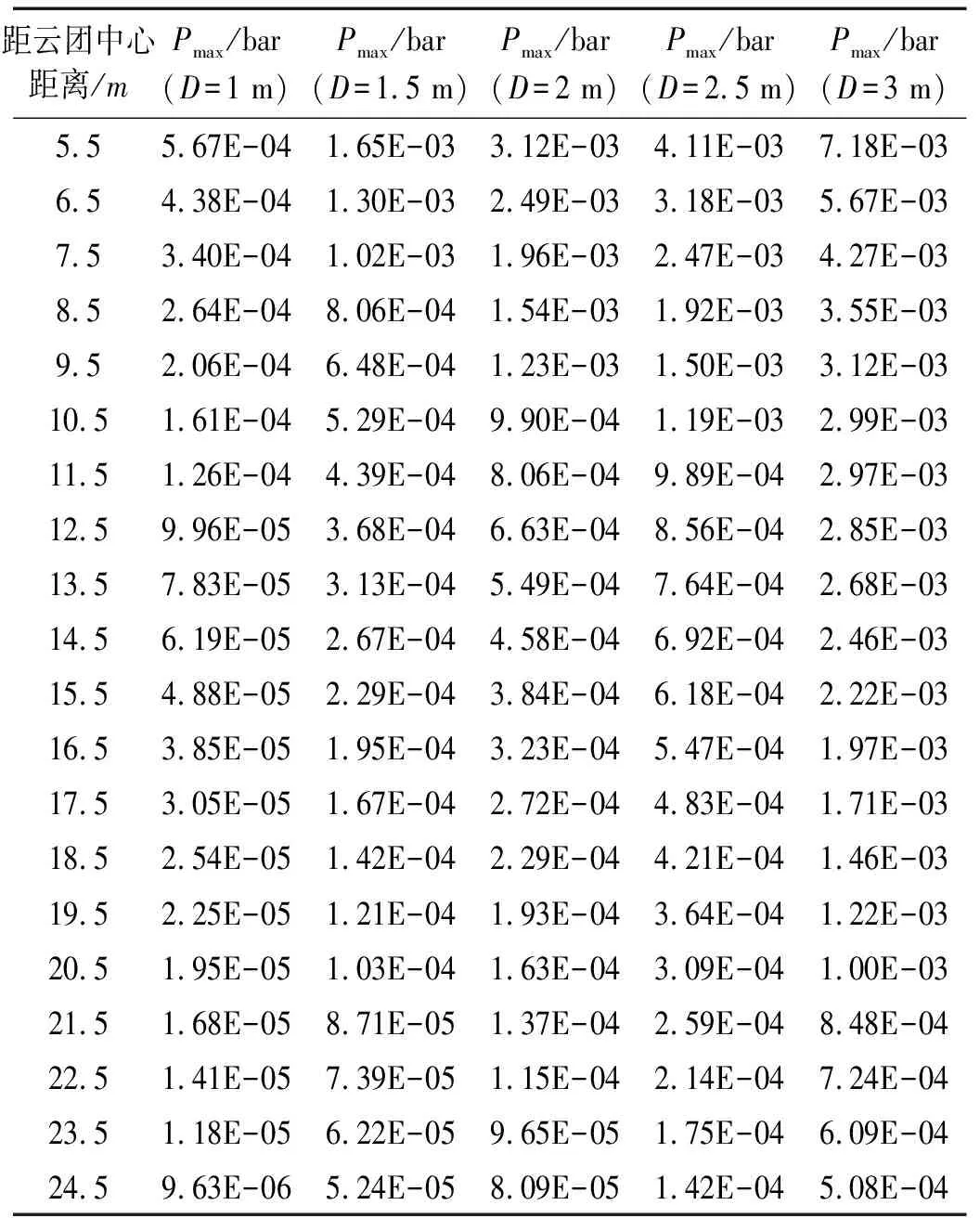
表2 不同體積甲烷云團爆炸最大超壓

對該數據作圖可以發現，除了D=3 m的氣體云團之外，其它體積的氣體云團爆炸產生的最大超壓與距云團中心距離近似于對數關系。當D=3 m時，曲線在10 m到22 m的區間整體呈現向上凸起的趨勢。這說明當甲烷-空氣云團充滿限制空間時，爆炸開始后部分燃料在未反應之前，在沖擊波的推動下從排放口沖出，后續的爆炸促進了湍流的增強，在加速爆炸波傳遞的效果下，出現曲線上抬的現象，如圖1所示。

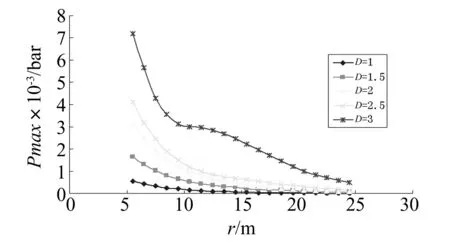
圖1 氣體爆炸最大超壓與距云團中心距離關系

3 模擬結果處理

3.1 折合距離

氣體爆炸產生的超壓與參與爆炸的氣體燃燒爆炸所釋放能量、從測量點到云團中心的距離等有關。參照TNO-MultiEnergy的方法，以距離縮放因子處理從云團中心到測試點的距離，計算縮放后的折合距離。

距離縮放因子的計算方法如式(1)所示。

(1)

式中：Svol為距離縮放因子；E為氣云燃燒熱，J；P0為大氣壓強，Pa。

折合距離的計算如式(2)所示:

(2)

式中：d為測試點距離云團中心的距離，m；rs為折合距離，m。

3.2 變換坐標系

在對數坐標系中，爆炸最大超壓-折合距離數據主要呈線性規律，如圖2所示。其中，云團邊長D=3 m的線性度比其它較差，其原因與前文解釋相同。

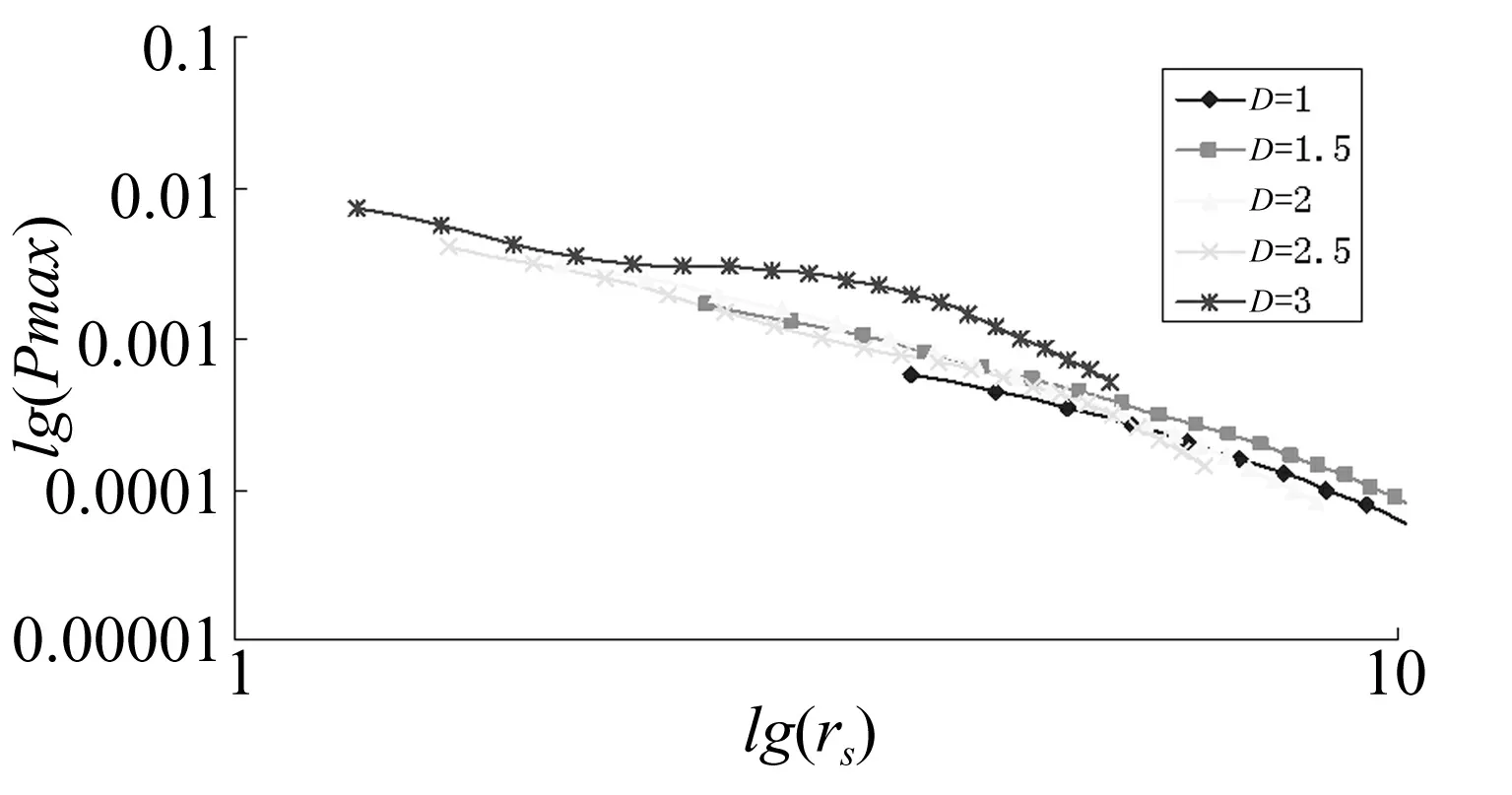
圖2 對數坐標中爆炸超壓與折合距離

4 公式模擬

4.1 公式建立

結合前文，聯系氣體爆炸超壓與縮放距離在對數坐標系中的圖形，經過數值模擬，可以得出各體積的甲烷-空氣云團爆炸超壓與氣體燃燒熱、距云團中心距離的關系。

當氣體云團為1 m×1 m×1 m時，氣體最大爆炸超壓與氣體燃燒熱、距云團中心距離的關系式如式(3)所示：

(3)

當氣體云團為1 .5 m×1.5 m×1.5 m時，三者關系如式(4)所示：

(4)

當氣體云團為2 m×2 m×2 m時，三者關系如式(5)所示：

(5)

當氣體云團為2.5 m×2.5 m×2.5 m時，三者關系如式(6)所示：

(6)

當氣體云團為3 m×3 m×3 m時，三者關系如式(7)所示：

(7)

綜上所述,1.6 m的高度處，氣體爆炸超壓和氣體燃燒熱、測試點距云團中心距離之間的關系如式(8)所示：

(8)

式中:A、B為與參與爆炸的甲烷-空氣體積有關的常數，如需要模擬的體積不在本文提出的五種案例之列，可以參考鄰近算式的相關數值，給出參考值。

4.2 模擬方法準確性

本文所述方法是將爆炸產生的最大超壓與折合距離的數值在雙對數坐標系中擬合為直線而建立的。數據的線性程度，決定了擬合公式的準確性。表3列出了不同體積的甲烷在對數坐標系中模擬公式的直線斜率與截距，以及該直線與對數坐標系中FLACS模擬曲線兩者的相關系數平方值。當擬合直線相對于原數據曲線的相關系數的平方值等于或接近于1時，所建立的公式最可靠。

經過分析可以發現，隨著D值的增大，其相關系數平方值不斷降低，但仍在0.9以上。這說明在所設場景中根據本文建模方法所建立的公式與FLACS模擬值具有較高的一致性，準確性較好。

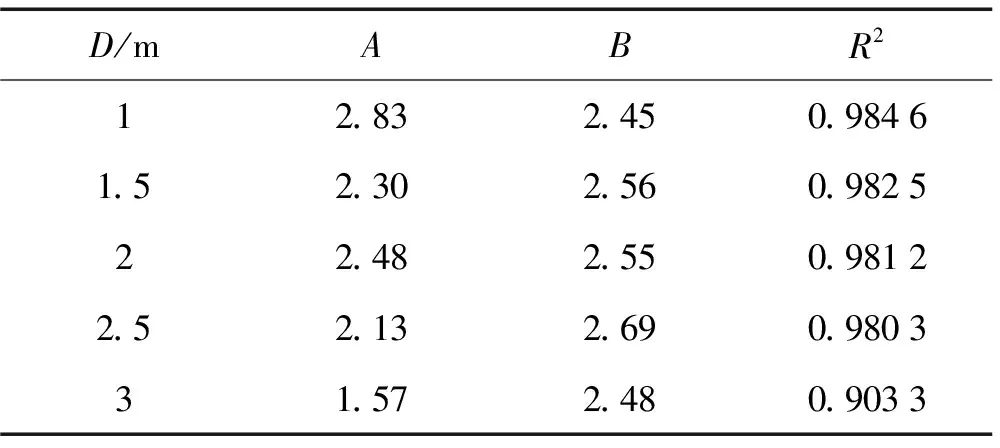
表3 不同甲烷體積模擬公式A、B系數及相關系數平方值

5 結 論

(1)本文設計了五種規模的甲烷-空氣氣體云團，研究了受限的甲烷-空氣氣云在單面遮擋下爆炸最大超壓傳播規律；

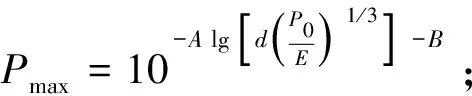
(3)本文提出了一種建立模擬計算公式的方法，由該方法所得的公式僅適用于本場景的遮擋條件下，不同體積甲烷的爆炸超壓、燃燒熱及距氣云中心距離等在1.6 m高度處的關系。可以根據實際需求，參照本文所提供的方法，建立不同遮擋、不同關注高度等條件下的模擬公式。

參 考 文 獻

[1]尚文啟.井噴點火過程天然氣爆炸后果分析[J].中國安全生產科學技術, 2006, 2(6): 7-9.

SHANG Wen-qi. Analysis on natural gas explosion aftereffect in the ignition procedure after blowout[J]. Journal of Safety Science And Technology, 2006, 2(6): 7-9.

[2]畢明樹,王淑蘭,丁信偉,等.無約束氣云弱點火爆炸壓力實驗研究[J].化工學報, 2001, 52(1): 68-71.

BI Ming-shu, WANG Shu-lan, DING Xin-wei, et al. Experimental study on explosion pressures of unrestricted gas cloud explosions[J]. Journal of Chemical Industry and Engineering, 2001, 52(1): 7-9.

[3]楊國剛,丁信偉,畢明樹.聚乙烯薄膜對可燃氣云爆炸影響的實驗研究與數值模擬[J].化工學報, 2005, 56(1): 180-184.

YANG Guo-gang, DING Xin-wei, BI Ming-shu. Experimental and simulated study of effect of polythene film on flammable vapor cloud explosion[J]. Journal of Chemical Industry and Engineering, 2005, 56(1): 180-184.

[4]李春孝.民用液化氣泄漏爆炸威力的探析[J].消防科學與技術, 2004, 23(2): 173-174.

LI Chun-xiao. Exploration of the risk of LPG leakage and explosion[J]. Fire Science and Technology, 2004, 23(2): 173-174.

[5]宋元寧,于立友,李彩霞. TNT當量法預測某石化設備爆炸后果評價[J].中國安全生產科學技術, 2005, 1(3): 66-68.

SONG Yuan-ning, YU Li-you, LI Cai-xia. TNT equivalent method predicts the consequence that some petrochemical industry equipment explodes[J]. Journal of Safety Science and Technology, 2005, 1(3): 66-68.

[6]張瑞華，陳國華，張 暉,等. TNO多能法在蒸汽云爆炸模擬評價中的工程應用[J].華南理工大學學報(自然科學版), 2006, 34 (5): 109-114.

ZHANG Rui-hua, CHEN Guo-hua, ZHANG Hui, et al. Engineering applications of TNO Multi-Energy method in VCE simulation assessment[J]Journal of South China University of Technology(Natural Science Edition), 2006, 34 (5): 109-114.

[7]鄭遠攀,張應安,馮長根,等.基于多能法和概率方程的井噴爆炸后果分析[J].科技導報, 2008, 26(21): 43-47.

ZHENG Yuan-pan, ZHANG Ying-an, FENG Chang-gen, et al. Consequence analysis for explosion of blowout based on multi-energy model and probit equation[J]. Science & Technology Review, 2008, 26(21): 43-47.

[8]王邵軍,呂 東,張 網.基于TNO多能法的蒸氣云爆炸傷害范圍評估研究[J].消防科學與技術, 2009，28(8): 180-181.

WANG Shao-jun, Lü Dong, ZHANG Wang. Research on injury distance of VCE Based on TNO multi-energy method[J].ire Science and Technology, 2009，28(8): 180-181.

[9]Van den Berg, A.C. The multi-energy method: A framework for vapor cloud explosion blast prediction[J]. Journal of Hazardous Materials, 1989, 12: 1-10.

[10]呂 東,李 晉,楊 軍.蒸氣云爆炸定量評估系統的研究與開發[J].消防科學與技術,2009，28(12): 82-84.

Lü Dong, LI Jin, YANG Jun. Research and design on quantitative risk assessment system of VCE[J]. Fire Science and Technology, 2009，28(12): 82-84.

[11]Baker Q A, et al. Vapor cloud explosion analysis[J]. Process Safety Progress, 1996 (2): 106-109

[12]Wingerden K van, et al. Predicting blast overpressures caused by vapor cloud explosions in the vicinity of control rooms[J]. Process Safety Progress, 1999, 18(1): 17-24.

[13]于梅春,張登春.障礙物場中預混燃燒火焰的數值模擬[J].中國安全科學學報, 2006, 16(3): 83-86.

YU Mei-chun, ZHANG Deng-chun. Numerical simulation of pre-mixed combustion flame in space with obstacle[J]. China Safety Science Journal, 2006, 16(3): 83-86.