基于廣義分形維數的刀具磨損狀態監測

張鍇鋒， 袁惠群， 聶 鵬

(1.東北大學 機械工程與自動化學院，沈陽 110819；2.沈陽航空航天大學 機電工程學院，沈陽 110136)

刀具狀態監測(Tool Condition Monitoring，TCM)是實現生產過程自動化，保證產品質量，提高生產效率，減少設備故障的重要手段。多年來，國內外學者在TCM領域做了大量的研究工作[1-2]。切削加工過程中采集的監測信號需要進行適當的處理，提取出對應不同磨損狀態的信號特征，才能對刀具磨損狀態進行分類。信號的特征提取算法種類很多[3]，然而，金屬切削是一個非常復雜的過程，其動力學行為具有很強的隨機性和非線性，因此，如何準確可靠地對大量的非平穩信號進行特征提取，是刀具磨損狀態在線監測研究的重要環節。分形理論作為非線性科學的重要組成部分，為研究復雜信號提供了有效的途徑，它以自然界中普遍存在的不規則的復雜現象為研究對象，描述傳統方法所不能描述的復雜的和不光滑的集合，目前在科學領域得到了廣泛的應用。在TCM領域，分形理論也得到了應用[4-7]，但多是只考慮信號的單一分形特征，即一個分形體由單一數值即分形維數來表征，

它只能從整體上反映信號的不規則性。然而對于復雜的分形體，它表現出的自相似特征是局域性的,具有空間分布的特征，單一的分形維數缺乏對局部特征的刻畫。而多重分形理論正是針對分形體的這一特性而提出的，多重分形維數能更精確的刻畫其局部的尺度行為，全面反映其分形特性[8]。描述多重分形的一種方法是廣義維數法，其在機械故障診斷、語音信號分析等領域已經得到了應用[9-11]。本文選取車削加工過程中AE信號的廣義維數為信號特征，計算廣義維數相關系數，并以此作為刀具磨損狀態決策分類的依據。

1 廣義分形維數定義與算法

廣義維數是描述多重分形的一種方法，對于概率向量P=(p1,p2,…pn)和任意給定的參數q∈R，Renyi定義廣義信息熵的表達式為[12]：

(1)

從而定義廣義維數為：

(2)

通過改變q值可以得到具有不同標度指數的子集，當q=0時得到容量維數(盒維數)

(3)

當q=1時得到信息維數

(4)

當q=2時得到關聯維數

(5)

覆蓋法是分形研究中最通用的方法,該方法是用尺度為ε的相同大小的盒子對整個集合進行覆蓋，所需盒子總數為N(ε)，通過計算采樣點落入每個盒子的概率，得到概率向量P，對于給定的參數q，根據式(1)得到該標度指數下的廣義信息熵。對盒子邊長在一定范圍內取值，可以得到一系列變化尺度ε，對數據點(lgε，Hp(q))進行線性擬合，擬合直線斜率的絕對值即為該尺度范圍內對應給定參數q的廣義維數Dq。

2 利用廣義維數識別刀具磨損狀態

2.1 監測信號的選擇與采集

目前用于刀具狀態監測的信號種類很多，如切削力、振動、聲發射(AE)和電流信號等，在實際應用中，這些信號都有其各自的特點，本文選擇聲AE信號作為監測信號。聲發射是材料受外力作用產生變形、斷裂或內部應力超過屈服極限進入不可逆的塑性變形階段，材料晶體間的彈性力與內聚力以瞬態彈性波形式釋放應變能的現象。金屬材料AE信號頻率范圍一般在50 kHz～1 MHz之間，避開了受切削加工過程中振動、噪聲影響較大的低頻區，抗干擾能力強，靈敏度較高。基于上述特性，為了減少噪聲的干擾，常用的信號處理方法是高通濾波或帶通濾波[13-14]，本文對采集的信號進行高通濾波，截止頻率選擇50 kHz。

監測信號采集在普通車床CA6140上進行，選用美國物理聲學公司(PAC)的R30型AE傳感器及PAC(2/4/6)型前置放大器，傳感器靠磁力吸附于刀柄，采樣頻率1 MHz，刀片材料為硬質合金YBC251，工件材料為高溫合金GH4169。在切削參數為：切削速度220 r/min，切削深度0.4 mm，進給量0.3 mm/r條件下，對應刀具磨損三個階段：初期磨損(VB值0.1 mm～0.2 mm)，中期磨損(VB值0.2 mm～0.3 mm)，后期磨損(VB值0.3 mm～0.4 mm)分別進行AE信號采集，每組信號采集時間1 s。根據采集信號對應的刀具磨損VB值，在上述三個磨損階段中，采用等間隔選取的方式(即VB值每增加近似0.01 mm，提取一組信號)，各選取10組AE信號作為樣本信號。

2.2 AE信號廣義維數計算

對采集的每組AE信號進行高通濾波，取濾波后樣本的前105個采樣點進行分析，不同刀具磨損狀態下AE信號的時域波形及頻譜如圖1所示。經研究發現，高通濾波前，樣本信號的頻域響應最大幅值出現在50 kHz以下，且隨磨損量的增加而增大；而高通濾波后，即在圖1所示的大于50 kHz頻率范圍內，隨著磨損量的增加，頻域響應最大幅值有所降低。

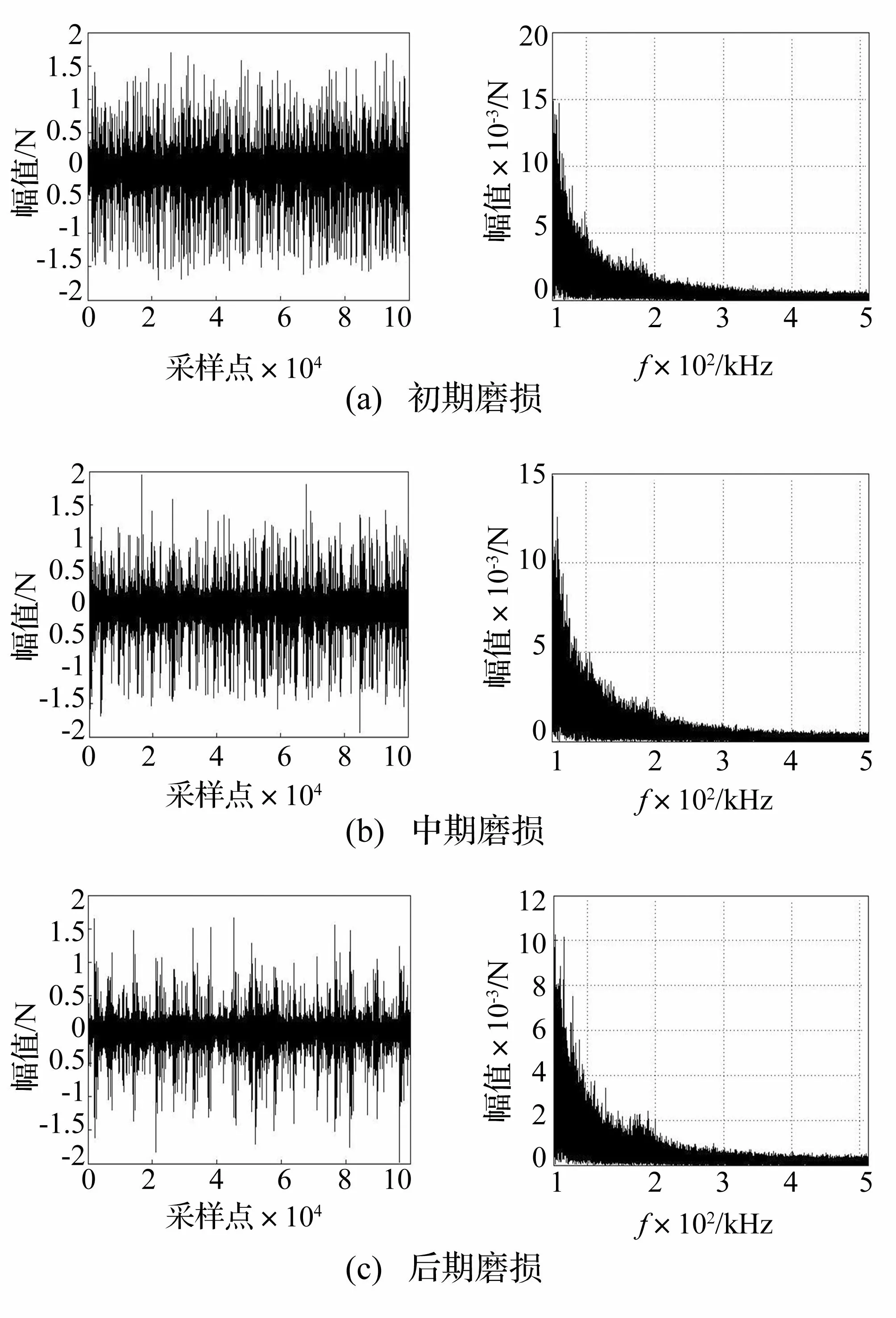
圖1 不同磨損狀態下AE信號的時域波形與頻譜

圖2 對應不同參數q的線性擬合

選擇尺度ε=2n×100，n=(1,2,…7)計算廣義分形維數。當參數q分別取值為0，1，2時，廣義維數Dq分別為盒維數、信息維數和關聯維數，其對應的最小二乘法線性擬合如圖2所示，在本文所選擇的尺度范圍內，擬合直線斜率即廣義維數隨q值的增大而減小。選擇q取值范圍為[0:0.1:2]，得到對應不同刀具磨損狀態的廣義維數譜如圖3所示。對應q=0時的盒維數(即常用的單一分形維數)，在不同的刀具磨損狀態下會有混疊現象出現，可見，此時應用單一的分形維數無法實現刀具磨損狀態的準確分類；隨著q值的增大，廣義分形維數的分類效果逐漸明顯，而且隨著刀具磨損量的增加，廣義分形維數值呈現整體下降趨勢。根據對數據樣本的研究發現，當q≥1時，廣義分形維數對刀具磨損狀態的分類效果最好，因此在后續的刀具磨損狀態識別中，選擇對應q值在[1∶0.1∶2]范圍內的廣義分形維數為特征向量。

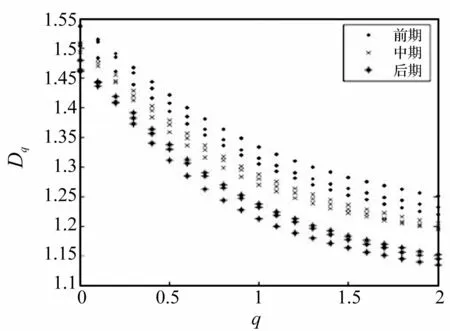
圖3 廣義維數譜

2.3 刀具磨損狀態識別

對刀具磨損狀態的識別，相當于比較待檢信號與各樣本信號間的相似程度。本文以AE信號的廣義維數為特征向量，通過計算待檢信號與各樣本信號特征向量間的距離，得到廣義維數相關系數。通過比較相關系數的大小來比較待檢信號與各樣本信號的相似程度，進而對刀具磨損狀態進行分類。相關系數越大，說明待檢信號與樣本信號越相似，磨損狀態也越相似。

廣義維數相關系數定義如下：

(6)

在三種磨損狀態下采集的AE信號中，各任選一組除樣本信號外的AE信號作為待檢信號，計算其廣義維數，根據式(6)計算得到的各待檢信號與各磨損狀態樣本信號廣義維數相關系數如表1所示。顯然，待檢信號1與樣本1的廣義維數相關系數最大，說明待檢信號1與樣本1最相似，判斷待檢信號1為初期磨損信號；待檢信號2、3分別與樣本信號2、3的廣義維數相關系數最大，判斷待檢信號2、3分別為中期磨損和后期磨損信號。這與實際測試時，各待檢信號對應的刀具磨損狀態完全一致。對30組采集的待檢信號進行試驗，通過比較廣義維數相關系數得到的識別準確率為90%；而通過比較單一分形維數(盒維數)相關系數得到的識別準確率只有73.3%。可見，廣義維數比單一分形維數具有更好的分類性能，通過比較廣義維數相關系數的大小，可以有效的對刀具磨損狀態進行決策分類。

表1 各待檢信號與各磨損狀態樣本信號的廣義維數相關系數

3 結 論

分形理論是研究復雜的不規則幾何特征的有效工具，而多重分形作為自相似分形的推廣，更能全面、精確的刻畫分形體自相似性的空間分布特征。本文將多重分形理論應用于刀具磨損監測研究，采用覆蓋法計算了刀具磨損AE信號的廣義維數，通過比較待檢信號與各類樣本信號的廣義維數相關系數，對刀具磨損狀態進行決策分類。通過對切削加工中采集的AE信號進行分析，證明了該方法能夠對刀具磨損狀態進行有效識別，將多重分形理論運用于刀具磨損監測之中具有較好的研究和應用價值。

參 考 文 獻

[1]Rehorn A G, Jin J, Orban P E. State-of-the-art methods and results in tool condition monitoring：a review[J]. Int J Adv Manuf Technol, 2005, 26：693-710.

[2]馬 旭,陳 捷.數控機床刀具磨損監測方法研究[J]. 機械, 2009, 36(6):70-73.

MA Xu, CHEN Jie. Study of monitoring method for CNC tool wear[J]. Machine, 2009, 36(6):70-73.

[3]關 山.在線金屬切削刀具磨損狀態監測研究的回顧與展望Ⅱ：信號特征的提取[J]. 機床與液壓,2010,38(17):121-125.

GUAN Shan. The review and perspective of the research of on-line and indirect metal cutting tool condition monitoringⅡ：Feature extraction of monitoring signals[J]. Machine Tool and Hydraulics, 2010,38(17):121-125.

[4]Kassim A A, Zhu M, Mannan M A. Tool condition classification using hidden markov model basedon fractal analysis of machined surface textures[J]. Machine Vision and Applications, 2006, 17:327-336.

[5]林 穎,劉亞俊,陳 忠. 基于分形理論和神經網絡的刀具磨損監測[J]. 中國機械工程, 2004,15(16):1426-1428.

LIN Ying, LIU Ya-jun, CHEN Zhong. Tool-wear detection using fractal theory and neural network[J]. China Mechanical Engineering，2004,15(16):1426-1428.

[6]王忠民,王信義,陳愛弟,等. 基于分形維數的刀具狀態在線監測新方法[J]. 北京理工大學學報, 2000, 20(4)：441-444.

WANG Zhong-min, WANG Xin-yi, CHEN Ai-di, et al. New method of on-line monitoring tool wear states Based on fractal dimension[J]. Journal of Beijing Institute of Technology, 2000, 20(4)：441-444.

[7]周承新,陳慧琴.基于加工表面盒維數的刀具磨損狀態研究[J].工具技術, 2010, 44(2):65-67.

ZHOU Cheng-xin, CHEN Hui-qin. Studies on tool wear condition based on the box dimension of workpiece texture[J]. Tool Engineering, 2010, 44(2):65-67.

[8]Mandelbrot B B. Multifractal measures, especially for the geophysicist[J]. Pageoph, 1989, 131(1/2):5-42.

[9]徐玉秀,侯榮濤,楊文平. 廣義分形維數在旋轉機械故障診斷中的應用研究[J]. 中國機械工程, 2003,14(21):1812-1814.

XU Yu-xiu, HOU rong-tao, YANG Wen-ping. Application of general fractal dimension to coupling fault diagnosis[J]. China Mechanical Engineering, 2003,14(21):1812-1814.

[10]Li B, Zhang P L, Wang Z J, et al. Morphological covering based generalized dimension for gear fault diagnosis[J]. Nonlinear Dyn, 2012, 67(4):2561-2571.

[11]Pitsikalis V, Maragos P. Analysis and classification of speech signals by generalized fractal dimension features[J]. Speech Communication, 2009, 51(12):1206-1223.

[12]Olsen L. Mixed generalized dimensions of self-similar measures[J]. Journal of Mathematical Analysis and Applications, 2005, 306(2):516-539.

[13]Osuri R H，Chatterjee S，Chandrashekhar S. On-line condition monitoring of tool wear in end milling using acoustic emission[J]. International Journal of Production Research, 1991,29(7):1339-1353.

[14]Bhaskaran J, Murugan M, Balashanmugam N, et al. Monitoring of hard turning using acoustic emission signal[J]. Journal of Mechanical Science and Technology,2012,26(2)：609-615.