金屬材料表面靜摩擦學特性的預測研究
——實驗佐證

田紅亮， 劉芙蓉， 趙春華， 方子帆， 朱大林， 陳保家， 秦紅玲， 張發軍

(1. 三峽大學 機械與材料學院，湖北 宜昌 443002；2. 三峽大學 水電機械設備設計與維護湖北省重點實驗室，湖北 宜昌 443002)

一個零件各處的截面特性(包括截面形狀、大小及材質)可以是相同的，如等截面軸；各部分截面的特性也可能不同，如臺階軸。等截面軸的零件由一個元件組成。臺階軸零件由多個元件組成，各個元件的連接部位稱為剛性結合面，兩相鄰元件在剛性結合面無相對位移。一臺機器由眾多零件組成，零件與零件之間的連接部位稱為柔性結合面。

摩擦學的研究對于國民經濟具有重要意義，摩擦導致的磨損是機械設備失效的主要原因，大約有80%的損壞零件是由于各種形式的磨損引起的。所以在機械結構中，研究和預測柔性結合面靜摩擦學特性是非常重要的。傳統的Coulomb摩擦第一定律[1-3]認為，摩擦力和法向載荷成正比，靜摩擦系數和所施加的法向載荷無關，亦不依賴于切向載荷，只隨接觸材料的不同而變化。但是隨著現代摩擦學的發展，發現Coulomb摩擦第一定律中摩擦力和法向載荷不成正比；靜摩擦系數對于同種材料不變的結論不適合實際工程；靜摩擦系數隨著接觸正壓力的增大而增大等。

文獻[1]改進分形幾何理論，探究金屬材料表面最大靜摩擦力的來源機理，建立法向總載荷、最大靜摩擦力、靜摩擦系數的改進分形模型，經過數值模擬，預測靜摩擦學特性，其結論和一些傳統摩擦學觀點迥然不同，分析產生不同的原因。但文獻[1]給出的接觸面積分別與分形維數及載荷的關系等，都還缺少足夠的實驗佐證。本文根據整個柔性結合面的結構函數，給出識別柔性結合面分形維數、分形粗糙度的理論及實驗方法，對文獻[1]靜摩擦系數的理論解進行定量實驗佐證。

1 采用修正分形理論的金屬表面靜摩擦模型

1.1 分形幾何理論的修正

處處連續、統計學自仿射特性、點點不可微的Weierstrass-Mandelbrot函數為：

(1)

式中：G為分形粗糙度；D為分形維數；n1為最低頻率的初始項，且γn1=1/L不同于文獻[15]的γn1=11L(L為取樣長度)；γ為譜密度的尺度參數；x為表面的取樣長度坐標。

應當指出式(1)截然不同于文獻[15]的式(5)。

自然海岸線的特點是將小尺度下的粗糙度在所有方向上放大相同倍數后，其概率分布與大尺度下的一致，這種曲線具有統計自相似特性。但是，絕大多數實際曲線并不具有統計自相似特性，而是具有統計自仿射特性，即要使較小尺度下的概率分布與較大尺度下的一致，就必須在不同方向上放大不同的倍數，典型的例子是分子的布朗運動曲線。因此，要方便地計算統計自仿射曲線的分形維數D、分形粗糙度G，就必須采用特殊方法。

Mandelbrot發現海洋面島嶼的面積分布有冪函數規律：

(2)

式中：Nr為面積A大于面積a的島嶼之總數；F′為待定未知數；a為一個島嶼的面積。

應當指出式(2)不同于文獻[15]的式(19)。

許多工程表面形貌的輪廓線都具有統計自仿射分形特性。若將粗糙表面(如金屬加工表面)放大到適當尺寸，就會發現類似于地球表面的高山峽谷，用一理想平面水平切取該表面形成的接觸點，也類似于海岸面的島嶼。因此，假設平面與粗糙表面接觸時接觸點面積的分布規律與海洋面島嶼面積的分布規律相同，即接觸點的數目見式(2)。但工程表面形貌的輪廓線與島嶼的海洋線不同的是，前者接觸點的輪廓曲線不是統計自相似曲線，而是統計自仿射曲線。

假設最大的微凸體接觸點面積為aL，數量為1個，將此假設條件代入式(2)得：

(3)

(4)

將式(4)代入式(2)可得連續隨機變量a的概率分布函數為：

(5)

連續隨機變量a的概率分布密度為：

(6)

按照核心關系式(6)可得柔性結合面無量綱法向總載荷[1]為：

1.2 金屬表面的靜摩擦系數

在兩接觸體中存在組合法向和切向力，無文獻記載應力場與實際接觸面積的完全解。1983年Hamilton設想：兩接觸體承擔法向彈性載荷Pe，由赫茲解得到的接觸區域形狀不受追加實用切向力Q的影響；假如比值Q/Pe<0.3，于是失效將首先發生在表面下，稍許遠離當Q=0時赫茲解對應的失效點；一經當比值Q/Pe>0.3以后，失效點躍遷到表面，失效發生在接觸邊界的邊遠邊緣上[4]。

現假如Q/Pe>0.3，接觸邊界邊遠邊緣的表面應力場分別為：

(8)

σ2=0

(9)

(10)

式中：ν為較軟材料的泊松比。

需要一提的是式(8)不同于文獻[7]的式(2)，式(10)不同于文獻[11]的式(1)。

按照式(8)、(10)可得柔性結合面無量綱最大靜摩擦力[1]為：

(11)

需要一提的是式(11)不同于文獻[11]的式(22)、(23)。

根據式(7)暨式(11)可得柔性結合面的靜摩擦系數為：

(12)

2 辨識兩個分形參數的結構函數方法

功率信號式(1)的自相關函數[20]為：

(13)

將式(1)代入式(13)得：

(14)

需要指出的是，從式(14)的倒數第二式可知：若m≠n時，各項都是零，則只剩下m=n時的一項。

象函數2πδ(ω-ω0)的傅里葉逆變換[20]為：

(15)

式中：ω為無阻尼自然角頻率。

則象原函數eiω0t的傅里葉變換為：

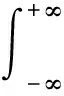
(16)

式中：δ(ω)為Dirac delta脈沖偶函數，單位是ω的倒數，且：

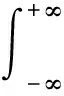
(17)

式中：c為非零實常數；y=|c|x為積分新變量。

因而有：

(18)

利用Euler公式，式(14)中通項象原函數cos2πγnτ的傅里葉變換[20]為：

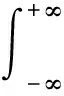
(19)

式中：f為無阻尼自然頻率，不同于無阻尼自然角頻率ω，ω=2πf。

將式(16)代入式(19)得：

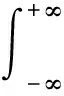
(20)

將式(18)代入式(20)得：

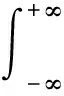
(21)

振幅頻譜式(21)的圖形見圖1。考慮粗糙表面微觀幾何形貌的隨機分布特點，如僅計及無阻尼自然頻率f>0單邊振幅頻譜，將-γn相應的振幅0.5疊加在γn相應的振幅0.5上，合成可得總振幅為1。故可將式(21)近似改寫成實際粗糙表面形貌的振幅頻譜：

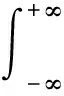
(22)

圖1 式(14)中通項的振幅頻譜

根據維納-辛欽關系式[20]可得離散自相關函數式(14)的離散功率譜密度函數為：

(23)

將式(22)代入式(23)得：

(24)

將離散功率譜密度函數式(24)轉化為連續功率譜密度函數[21]：

(25)

式中：Δf為無阻尼自然頻率的增量；Δn為無阻尼自然頻率指數的增量；n(f)為無阻尼自然頻率零點指數，且：

n(f)=logγf

(26)

將式(26)代入式(25)得：

(27)

需要注意，式(27)和文獻[15]的式(6)、文獻[22]的式(2)、文獻[23]的式(2a)、文獻[24]的式(10)均相異。

按照定積分的換元法得：

(28)

式中：x>0；β>0；z=xt為定積分新變量；Γ(β)為gamma函數。

由式(28)得：

(29)

隨便查高等數學不定積分表得：

(30)

利用變量代換，下述定積分為：

(31)

令d=e=i=1，h=2，由式(31)得：

(32)

用β-2代換式(32)中的g且使用余元公式得：

(33)

使用式(29)可將下列單重定積分化為二重定積分：

(34)

式中：β=5-2D∈(1,3)。

由式(28)可得t>0，將式(30)代入式(34)得：

(35)

將式(33)代入式(35)得：

(36)

將式(34)中的注釋β=5-2D代入式(36)得：

(37)

重點說明，式(37)亦皆相異于文獻[23]的式(14)、文獻[26]第215頁的式(2)。

由Γ函數的遞推公式及余元公式，式(37)可變形為：

(38)

式(1)派生出函數z(x1)及z(x2)之間的結構函數為：

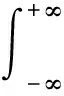
(39)

式中：〈 〉為無阻尼自然頻率平均符號。

特別強調的是，式(39)亦全不同于文獻[15]的式(8)、文獻[27]的式(11)、文獻[28]的式(2.3)。

根據式(27)可得雙邊連續功率譜密度函數為：

(40)

奇函數sin(x1-x2)f在對稱區間(-∞,+∞)上對f的定積分是零，根據Euler公式，將式(40)代入式(39)得：

(41)

式中：x=|x1-x2|f為定積分新變量。

將式(38)代入式(41)得：

〈[z(x1)-z(x2)]2〉=

(42)

令x1=x，x2=x-τ(τ為尺度滯后)，可得整體柔性結合面的結構函數為：

(43)

當量表面高度式(1)和兩個粗糙表面1、2高度之間的關系為：

z(x)=z1(x)-z2(x)

(44)

式中：zj(x)為粗糙表面j的高度，j=1,2。

參考式(39)中“〈 〉”符號的運算規則，將式(44)代入式(43)得：

S(τ)=〈[z1(x)-z2(x)-z1(x-τ)+z2(x-τ)]2〉=〈[z1(x)-z1(x-τ)]2〉-2〈[z1(x)-z1(x-τ)][z2(x)-z2(x-τ)]〉+〈[z2(x)-z2(x-τ)]2〉

(45)

由于兩粗糙表面在傳統統計學上互不相關，則下列交叉乘積項為零：

〈[z1(x)-z1(x-τ)]×[z2(x)-z2(x-τ)]〉=0

(46)

仿照式(43)，因此式(45)可變形為：

S(τ)=S1(τ)+S2(τ)

(47)

式中：Sj(τ)為粗糙表面j的結構函數，j=1,2。

令γ=γ1=γ2，不失去普遍性，將式(47)展開得：

(48)

式中：γ為整體柔性結合面非整數相位隨機參數；γj為表面j的相位隨機參數，j=1,2；D為整體柔性結合面的分形維數；Dj為表面j的分形維數，j=1,2；G為整體柔性結合面的分形粗糙度；Gj為表面j的分形粗糙度，j=1,2。

文中大量涉及gamma函數，文獻[29]僅提供gamma函數在閉區間1≤x≤2的以下近似解：

Γ(x)≈1-0.574 864 6(x-1)+0.951 236 3(x-1)2-0.699 858 8(x-1)3+0.424 554 9(x-1)4-0.101 067 8(x-1)5,1≤x≤2

(49)

但式(49)不能解決02更廣大開區間對應的gamma函數Γ(x)具體值。為徹底得到gamma函數在0

x=0.01：0.1：2 004；% 2 004可取適當較大值

plot(x，gamma(x))

文獻[29]近似解與文中解的比較見圖2，可見采用文中解可獲取gamma函數。

圖2 文獻[29]解和文中解的比較

若G1=3.6×10-10m、G2=2.4×10-10m、γ=γ1=γ2=1.5時，粗糙表面1、2與整體柔性結合面的結構函數見圖3。

圖3 三種結構函數

2.1 兩粗糙表面分形維數相等

此刻式(48)可簡化為：

(50)

為使關于自變量尺度滯后τ的恒等式(50)成立，可得要辨識整體柔性結合面的分形維數、分形粗糙度為：

D=D1=D2

(51)

(52)

圖3(a)結果說明，在雙對數坐標系下，整體柔性結合面的結構函數S(τ)和τ是線性關系，且和S1(τ)、S2(τ)均平行，整體柔性結合面在S(τ)軸上的縱截距都分別大于粗糙表面1在S1(τ)軸上的縱截距、粗糙表面2在S2(τ)軸上的縱截距，整體柔性結合面具有單重分形特性，整體柔性結合面的分形維數D和兩粗糙表面的分形維數D1、D2相等(式(51))，整體柔性結合面的分形粗糙度G更大，即整體柔性結合面比互相接觸兩個粗糙表面更粗糙(式(52))。

2.2 兩粗糙表面分形維數不相等

圖3(b)顯示，在雙對數坐標系下，整體柔性結合面的結構函數S(τ)和τ不再為線性關系，而表現為1條向上凹的曲線弧，且兩粗糙表面的分形維數D1與D2偏離越懸殊，此曲線弧的彎曲程度越明顯，曲線弧的第一段主要表示粗糙表面2的S2(τ)的分形性質，第二段主要表示粗糙表面1的S1(τ)的分形性質，說明整體柔性結合面具有雙重分形性質，繼而增加了求解非線性方程式(48)的難度。

嚴格站在高等數學的立場上，無條件能使關于自變量τ的方程式(48)恒成立。為求解此方程，首先按照兩粗糙表面1、2的結構函數與式(47)，得到整體柔性結合面的結構函數，該結構函數在雙對數坐標系下雖不是1條直線，但利用最小二乘法可近似回歸其為1條直線，然后可辯識整體柔性結合面的分形維數D、分形粗糙度G。

不失去普適性，根據式(43)可得一條直線方程：

(53)

假定：

k=2(2-D)

(54)

g=-lgG

(55)

將式(54)、(55)代入式(53)得：

(56)

再假定：

(57)

將式(57)代入式(56)得：

lgS(τ)=klgτ+b

(58)

直線方程式(58)見圖4。

圖4 整體柔性結合面的常用對數結構函數

由式(54)，D=2-0.5k依賴k。由式(57)，g依賴b、D，因D依賴k，故g依賴b、k。由式(55)，G=10-g依賴g，故G依賴b、k。

3 靜摩擦系數理論解的實驗佐證

3.1 實驗方案

電動機在時間t秒鐘內提供的額定功為：

(59)

式中：TN為電動機額定轉矩，N·m；n1為電動機實際轉速，r/min。

電動機在時間t秒鐘內提供的平均額定功率為：

(60)

執行裝置旋轉工作臺消耗的功率為：

(61)

式中：T2為旋轉工作臺轉矩，N·m；n2為旋轉工作臺轉速，r/min；F為兩靜壓導軌表面間最大靜摩擦力[1]，N；r為最大靜摩擦力作用的當量半徑，mm；f為兩靜壓導軌表面間的靜摩擦系數；P為加載重物的重量，即法向總載荷[1]，N。

電動機的額定功率是相應于額定環境溫度40 ℃時的允許輸出功率，故當環境溫度高于或低于40 ℃時，電動機允許輸出的功率可適當減小或增加。根據式(60)，增減后的允許輸出功率為：

(62)

式中：α為滿載時的不變損耗(包括鐵損耗、機械損耗與附加損耗)和可變損耗(銅損耗)的比值；θ為實際環境溫度；θN為額定溫升；ξ為電動機負載率。

在電動機低轉速情況下，使旋轉工作臺剛剛開始運動，得到靜摩擦系數。工作臺旋轉消耗的功率等于驅動電機的輸出功率，根據傳遞過程中的機械損失，可以得到功率平衡關系：

P2=ηP1

(63)

將式(61)、(62)代入式(63)得：

(64)

式中：η為普通圓柱蝸桿傳動的總效率，且：

η=η1η2η3

(65)

式中：η1為嚙合摩擦損耗效率；η2為軸承摩擦損耗效率；η3為濺油損耗效率，且：

(66)

式中：γ為普通圓柱蝸桿分度圓柱上的導程角；φv為當量摩擦角。

按照式(64)，如果獲得電動機在線運行時的n1、ξ，則能得到不同法向總載荷P時的靜摩擦系數。結合面接觸模型是描述兩粗糙表面相接觸表面微凸體的接觸特性，本文的理論部分[1]并沒有分析液體與粗糙表面接觸的接觸特性。實驗是液體靜壓導軌接觸表面，兩靜壓導軌通過油膜(通常油膜厚度為5、7、9、14 μm等)而相互分開，靜壓導軌的兩金屬表面在微觀狀態下是不直接接觸的，是液體與金屬粗糙表面接觸(否則就不是靜壓導軌)，若考慮液體、油膜等非直接接觸特性而求解的摩擦系數是微觀摩擦系數。為使實驗與兩金屬粗糙表面相接觸的理論較好地吻合，獲得能應用于實際工程的整個結合面的宏觀摩擦系數，一方面，在實驗前，先將兩個靜壓導軌1、靜壓導軌2從機床部件中相互分離，然后將兩個靜壓導軌1、靜壓導軌2的結合表面在丙酮中通過超聲波清洗50 min，最后在去離子水中沖洗后，用流動的氮氣吹干，即讓兩個靜壓導軌成為兩干接觸表面，也即兩個靜壓導軌在短時間內處于非正常工作狀態，使用環境愈加惡劣；另一方面，在實驗的過程中在滿足工況的前提條件下，裝配兩個靜壓導軌1、靜壓導軌2時，盡可能使油膜厚度小，如取1 m，使靜壓導軌的兩金屬表面逼近接觸。如上所述，實驗方案見圖5，h為公稱油膜厚度。

圖5 實驗方案

3.2 實驗過程

在武漢重型機床集團有限公司YK31320型普通滾齒機上進行實驗，見圖6。實驗時的面板數據見圖7。

圖6 YK31320型普通滾齒機

3.3 分形參數實驗辨識與靜摩擦系數的求解

研磨方式加工兩液體靜壓導軌接觸表面。采用英國Micro Materials Ltd制造的NanoTest?600型納米壓痕儀測定粗糙表面薄膜的硬度H，為了減少基體對薄膜硬度測量的影響，選擇壓入深度為100nm，每個樣品取5個點進行測量，取平均值。液體靜壓導軌的參數見表1。

表1 兩液體靜壓導軌表面的參數

使用英國公司Charlotte Research Institute的Taylor-Hobson Form TalySurf 5-120型表面輪廓儀，放大倍率為×1 000，采樣長度為15 mm，采樣間距為1 m，采樣段數為5，最小二乘濾波，離散化采樣點數為15 000。測試環境溫度為23.5 ℃，空氣相對濕度為58%。

設采樣長度T=15 mm；無阻尼自然頻率間隔為Δf=1/T；采樣表面輪廓高度的離散數據點數為l，取l=15 000；采樣間隔為Δx，取Δx=1 μm；空間采樣點數為Ns=T/Δx=15 000，將數據補齊為大于l且為2的整數冪次方的數，選擇Ns=214>l；采樣頻率為fs=1/Δx；最高頻率為fmax，取fmax=0.5fs；設定無阻尼自然頻率變化范圍為f=fmax(0∶0.5Ns-1)/Ns；對表面輪廓信號表達式(1)的z(x)進行補零的Fourier變換，把z(x)的尾部補零使z(x)的長度達到Ns，可得補零的Fourier變換Y=fft(z,Ns)；按照Y獲得功率譜密度函數P(f)=|Y|2/Ns，根據式(39)得到柔性結合面的結構函數S(τ)，然后使用最小二乘法的一次多項式擬合實測數據(lgτ,lgS(τ))，可獲取常用對數結構函數(圖4)。

表2 整體柔性結合面研磨時的編程情況

圖7 實驗面板數據

整體柔性結合面研磨時的情形見表2，不均勻刻度結構函數方法應用的是國際單位，使用的符號是斜率k1、縱截距b1、分形粗糙度的指數g1、分形維數D1、分形粗糙度G1，國外研究人員習慣使用；均勻刻度結構函數方法以長度單位微米為出發點，應用的符號是斜率k2、縱截距b2、分形粗糙度的指數g2、分形維數D2、分形粗糙度G2，中國研究人員習慣使用。這二種方法辨識的五個參數分別為k1=0.993 4，b1=-8.165 2，D1=1.503 3，g1=8.697 5，G1=2.006 6×10-9m；k2=0.993 4，b2=-2.125 8，D2=1.503 3，g2=2.697 5，G2=2.006 6×10-9m。則整體柔性結合面的兩個重要表征參數為D=1.503 3，G=2.006 6×10-9m。

將辨識的整體柔性結合面參數D、G代入式(1)，可得二維表面輪廓高度的仿真線，二維表面輪廓高度的實測線、仿真線見圖8(a)。二維表面輪廓高度的模擬函數式(1)可由下面三維表面輪廓高度的Ausloos-Berman函數簡化而得：

(67)

式中：x,y為粗糙表面輪廓的位移坐標；L為取樣長度；M為曲面褶皺的重疊數；γ為大于1的常數，通常取γ=1.5；n為無阻尼自然頻率序數；nmax為最高頻率序數，nmax=int[ln(L/Ls)/lnγ]，Ls為截止長度，通常近似為材料的原子間距離；φm,n為隨機相位，取值范圍為[0,2π]。

將辨識的整體柔性結合面參數D、G代入式(67)，可得三維表面輪廓高度的仿真線，三維表面輪廓高度的實測線見圖8(b)、仿真線見圖8(c)、兩者之間的相對誤差見圖8(d)。根據圖8(d)，仿真線和實測線之間的相對誤差較小，說明辨識的整體柔性結合面參數實用有效。

圖8 表面輪廓高度的實測線和仿真線的比較

圖9 理論靜摩擦系數和實驗的比較

例如在加載重物的重量P=100 kN時，將表1中的數據與D=1.503 3，G=2.006 6×10-9m代入式(12)、(64)，分別可得整體柔性結合面的理論靜摩擦系數為f=0.480 51，實驗靜摩擦系數為f=0.466 93。

3.4 理論靜摩擦系數和實驗的誤差

在加載不同質量的重物情況下，理論靜摩擦系數和實驗的比較見圖9。觀察圖9(a)，在狹窄的小載荷0～1.6 kN范圍內，即電動機在低轉速工況下，實驗靜摩擦系數隨法向總載荷的增大而變小(由于使旋轉工作臺開始旋轉，施加在旋轉工作臺上的切向總載荷愈來愈大)，且實驗靜摩擦系數會呈現忽高忽低的突變波動情況(由于電動機的低轉速迫使機床靜壓導軌的動態性能處于不穩定的爬行，強烈影響靜壓導軌的表面粗糙度，引起摩擦副的劇烈磨損)；在寬廣的中等載荷1.6～100 kN范圍內，即電動機在近似穩定中等轉速工況下，實驗靜摩擦系數隨法向總載荷的增大而增大，且理論靜摩擦系數比實驗大(由于實際兩靜壓導軌表面之間存在最小公稱油膜厚度的流體膜，常使一個靜壓導軌處于似浮非浮狀態)。根據圖9(b)，理論靜摩擦系數和實驗的絕對誤差在-0.033 02～0.019 26之間。根據圖9(c)，理論靜摩擦系數和實驗的相對誤差在-8.323%～5.512%之間。值得提醒：由于實際靜摩擦系數的變化范圍狹窄，所以給出絕對誤差比提供相對誤差更有說服力。

4 結 論

(1)給出關于粗糙表面微凸體接觸點面積a的概率分布密度n(a)的推導過程。該概率分布密度適用于機械加工粗糙表面，不管磨削、銑削、車削表面都滿足此概率分布密度的關系式。

(2)給出計算整體柔性結合面兩個分形參數的結構函數方法。該結構函數方法可以從測量的實際數據入手，能求解特定整體柔性結合面分形維數、分形粗糙度的具體數字。本文嚴格區分無阻尼自然頻率f和無阻尼自然角頻率ω，ω=2πf，本文求解的是以f為自變量的功率譜密度函數和結構函數。文獻[30]將f和ω都當作ω，不合理。對于以ω為自變量的功率譜密度函數和結構函數的修正計算是后續重點研究的內容。

(3)對文獻[1]的理論計算和分析進行實驗佐證。在一定加載重物的范圍內，理論靜摩擦系數和實驗的絕對誤差在-0.033 02～0.019 26之間，理論靜摩擦系數和實驗的相對誤差在-8.323%～5.512%之間。

參 考 文 獻

[1]田紅亮，趙春華，方子帆，等. 金屬材料表面靜摩擦學特性的預測研究——理論模型[J]. 振動與沖擊，2013，32(12)：40-44,66.

TIAN Hong-liang, ZHAO Chun-hua, FANG Zi-fan, et al. Predication investigation on static tribological performance of metallic material surfaces- theoretical model [J]. Journal of Vibration and Shock，2013，32(12)：40-44,66.

[2]趙 飛，逄顯娟，杜三明，等. MoSx摻雜DLC薄膜的摩擦磨損行為Ⅰ：載荷的影響[J]. 摩擦學學報，2012，32(5)：516-523.

ZHAO Fei, PANG Xian-juan, DU San-ming, et al. Friction and wear behaviors of MoSx-doped DLC films Ⅰ：effect of normal load [J]. Tribology，2012，32(5)：516-523.

[3]趙 飛，逄顯娟，杜三明，等. MoSx摻雜DLC薄膜的摩擦磨損行為Ⅱ：速度的影響[J]. 摩擦學學報，2012，32(5)：524-530.

ZHAO Fei, PANG Xian-juan, DU San-ming, et al. Friction and wear behaviors of MoSx-doped DLC films Ⅱ：effect of sliding speed [J]. Tribology，2012，32(5)：524-530.

[4]Chang W R, Etsion I, Bogy D B. Static friction coefficient model for metallic rough surfaces [J]. Transactions of the ASME Journal of Tribology，1988，110(1)：57-63.

[5]Greenwood J A, Williamson J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences，1966，295(1442)：300-319.

[6]You J M, Chen T N. A static friction model for the contact of fractal surfaces [J]. Proceedings of the Institution of Mechanical Engineers, Part J：Journal of Engineering Tribology，2010，224(5)：513-518.

[7]尤晉閩，陳天寧. 結合面靜摩擦系數的統計模型[J]. 振動與沖擊，2010，29(12)：26-29.

YOU Jin-min, CHEN Tian-ning. Statistical model of static friction coefficient between joint surfaces [J]. Journal of Vibration and Shock，2010，29(12)：26-29.

[8]呂振林，劉晶歌，肖琪聃，等. Ti3AlC2陶瓷的制備及其摩擦磨損性能[J]. 硅酸鹽學報，2012，40(4)：503-506.

Lü Zhen-lin, LIU Jing-ge, XIAO Qi-dan, et al. Fabrication of Ti3AlC2by reactive sintering and its friction and wear behavior [J]. Journal of the Chinese Ceramic Society，2012，40(4)：503-506.

[9]盛選禹，雒建斌，溫詩鑄. 基于分形接觸的靜摩擦系數預測[J]. 中國機械工程，1998，9(7)：16-18.

SHENG Xuan-yu, LUO Jian-bin, WEN Shi-zhu. Static friction coefficient model based on fractal contact [J]. China Mechanical Engineering，1998，9(7)：16-18.

[10]Majumdar A，Bhushan B. Fractal model of elastic-plastic contact between rough surfaces [J]. Transactions of the ASME Journal of Tribology，1991，113(1)：1-11.

[11]Sui C F, Sheng X Y. Fractal transition model in predicting static friction coefficient [J]. Multidiscipline Modeling in Materials and Structures，2009，5(4)：345-348.

[12]田紅亮，趙春華，朱大林，等. 彈塑性三維各向異性分形表面的接觸分析[J]. 三峽大學學報(自然科學版)，2012，34(1)：69-73.

TIAN Hong-liang, ZHAO Chun-hua, ZHU Da-lin, et al. Contact analysis of elastoplastic three-dimensional anisotropic fractal surfaces [J]. Journal of China Three Gorges University (Natural Sciences)，2012，34(1)：69-73.

[13]田紅亮，朱大林，秦紅玲. 固定接觸界面法向靜彈性剛度的改進彈簧分形模型[J]. 三峽大學學報(自然科學版)，2012，34(6)：83-88.

TIAN Hong-liang, ZHU Da-lin, QIN Hong-ling. Improved spring fractal model for normal static elastic stiffness of stationary contact interface [J]. Journal of China Three Gorges University (Natural Sciences)，2012，34(6)：83-88.

[14]魏 龍，劉其和，張鵬高. 基于分形理論的滑動摩擦表面接觸力學模型[J]. 機械工程學報，2012，48(17)：106-113.

WEI Long, LIU Qi-he, ZHANG Peng-gao. Sliding friction surface contact mechanics model based on fractal theory [J]. Journal of Mechanical Engineering, 2012，48(17)：106-113.

[15]賀 林，朱 均. 粗糙表面接觸分形模型的提出與發展[J]. 摩擦學學報，1996，16(4)：375-384.

HE Lin, ZHU Jun. Fractal model for contact of rough surfaces [J]. Tribology，1996，16(4)：375-384.

[18]田紅亮，劉芙蓉，朱大林. 4種NET歐拉-伯努利直梁的動力學特性[J]. 三峽大學學報(自然科學版)，2013，35(4)：85-93.

TIAN Hong-liang,LIU Fu-rong, ZHU Da-lin. Dynamic properties of four NET Euler-Bernoulli straight beam [J]. Journal of China Three Gorges University (Natural Sciences)，2013，35(4)：85-93.

[19]李彥青，殷德順，吳 浩. 變分數階微積分在描述材料力學性質演變方面的應用[J]. 三峽大學學報(自然科學版)，2012，34(6)：63-67,76.

LI Yan-qing, YIN De-shun, WU Hao. Application of variable-order fractional calculus to description of evolution of mechanical properties of materials [J]. Journal of China Three Gorges University (Natural Sciences)，2012，34(6)：63-67,76.

[20]盧文祥，杜潤生. 機械工程測試·信息·信號分析[M]. 2版. 武昌：華中科技大學出版社，2004.

[21]Berry M V, Lewis Z V. On the Weierstrass-Mandelbrot fractal function [J]. Proceedings of the Royal Society of London：Series A Mathematical and Physical Sciences, 1980，370(1743)：459-484.

[22]Bhushan B, Majumdar A. Elastic-plastic contact model for bifractal surfaces [J]. Wear，1992，153(1)：53-64.

[23]Ganti S, Bhushan B. Generalized fractal analysis and its applications to engineering surfaces [J]. Wear，1995，180(1-2)：17-34.

[24]Majumdar A, Tien C L. Fractal network model for contact conductance [J]. Transactions of the ASME Journal of Heat Transfer，1991，113(3)：516-525.

[25]《數學手冊》編寫組. 數學手冊[M]. 北京：高等教育出版社，2008：590.

[26]Wang S, Komvopoulos K. A fractal theory of the temperature distribution at elastic contacts of fast sliding surfaces [J]. Transactions of the ASME Journal of Tribology，1995，117(2)：203-215.

[27]Majumdar A, Bhushan B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J]. Transactions of the ASME Journal of Tribology，1990，112(2)：205-216.

[28]Berry M V. Diffractals [J]. Journal of Physics A：Mathematical and General，1979，12(6)：781-797.

[29]郭建英，孫永全，王銘義，等. 基于計算機仿真的風電機組系統可靠性綜合[J]. 機械工程學報，2012，48(2)：2-8.

GUO Jian-ying, SUN Yong-quan, WANG Ming-yi, et al. System reliability synthesis of wind turbine based on computer simulation [J]. Journal of Mechanical Engineering，2012，48(2)：2-8.

[30]田紅亮，劉芙蓉，方子帆，等. 結合部靜摩擦因數修正與定量實驗驗證[J]. 農業機械學報，2013，44(10)：282-293.

TIAN Hong-liang,LIU Fu-rong, FANG Zi-fan, et al. Correction of static friction coefficient for joint interface and quantitative test confirmation [J]. Transactions of the Chinese Society for Agricultural Machinery，2013，44(10)：282-293.