排列熵算法參數的優化確定方法研究

饒國強， 馮輔周， 司愛威， 謝金良

(裝甲兵工程學院 機械工程系, 北京 100072)

排列熵是衡量一維時間序列復雜度的平均熵參數，其計算簡單、抗噪聲能力強，是一種新的動力學突變檢測方法，能夠較好地反映時間序列數據的微小變化[1]。目前，排列熵算法在醫學、環境等領域應用廣泛[2-5]，主要是對復雜系統進行異常檢測，應用效果比較突出。

排列熵算法受自身參數的影響比較大，參數的選擇仍然僅憑經驗或直覺，從而使計算結果存在很大的不確定性。本文引入相空間重構方法，選擇合適的排列熵算法參數確定方法，以期提高排列熵計算結果的準確性和算法效率。

1 排列熵算法

排列熵算法的基本原理如下：

設一時間序列{X(i),i=1,2,…,n}，對其進行相空間重構，得到矩陣：

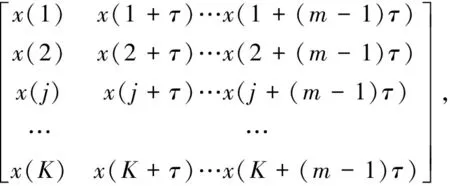
(1)

式中：m、τ分別為嵌入維數和延遲時間，K=n-(m-1)τ。矩陣中的每一行可看作一個重構分量，共有K個重構分量。然后對每個重構分量的元素，根據數值大小按照升序重新排列，提取各個元素在原重構分量中所在列的索引，可以得到不同的符號序列，m維相空間映射不同的符號序列總共有m!。若k種不同符號序列出現的概率為P1,P2,…,Pk，則按照Shannon熵的形式，排列熵可以定義為：

(2)

將HPE(m)進行歸一化處理，即：

0≤HPE=HPE/ln(m!)≤1

(3)

根據排列熵算法的基本原理，相空間重構是模型的第一步，其延遲時間τ和嵌入維數m是排列熵算法的主要參數，對于排列熵的計算結果有較大的影響。

2 相空間重構

相空間重構方法是由Takens在1981年提出，其基本思想是：系統中任一分量的演化都是由與之相互作用著的其它分量所決定的，因此單一變量的時間序列應該隱含整個系統的運動規律，考察一個分量，測量它在某些固定的時間延遲點上的數值，然后將其重構為多維狀態空間中的高維向量，并使得重構坐標從低維到高維轉換時保持較強的獨立性，最終的重構相空間具有較低的冗余度。相空間重構有兩種方法：導數重構法和延遲重構法。延遲重構法在混沌研究中得到了廣泛的應用，而導數重構法卻很少得到實際應用。

在延遲重構法中，關于τ和m的選取，主要有兩種觀點[6]:①兩者互不相關，即τ和m獨立確定；②兩者相關，即τ和m互相依賴。對于第一種觀點，通常應用互信息法和偽鄰近點法相結合，先利用互信息法確定τ，然后在τ已知的情況下運用偽鄰近點法選取m；第二種觀點的代表性方法是關聯積分法(C-C算法)，該方法是通過構造統計變量和延遲時間的關系來確定最佳延遲時間和嵌入窗寬，再根據嵌入窗寬確定嵌入維數。

3 排列熵算法參數優化確定

對于設備不同運行狀態下的時間序列信號，采用相同參數對不同狀態下的時間序列進行相空間重構，所得出的時間序列排列熵值將會不同。因此，對設備在某一運行狀態下的時間序列進行相空間重構所確定的算法參數，可用于設備運行全過程時間序列的排列熵特征提取，并以排列熵值的變化來反映設備的不同運行狀態，從而達到異常檢測的目的。基于該思路，提出構建最佳相空間為目標的算法參數確定方法。

3.1 τ和m的獨立確定方法

(1)互信息法

互信息法的基本原理是：對于系統的某一時間序列{x(t),t=1,2,…,N}，為了建立延遲時間τ的關系式，選取延遲序列x(t+τ)構成新的點列y(t)，通過計算x(t)和y(t)的相關性來確定延遲時間τ。假設構成點對的總數為n，n=N-τ。則對于兩個離散時間序列{x(1),x(2),…,x(n)}和{y(1),y(2),…,y(n)}對應的系統X和Y，根據信息論的知識，從兩個系統測量中所獲得的平均信息量，即信息熵分別為：

(4)

(5)

其中，Px(xi)和Py(yi)分別為系統X和Y中事件xi和yi的概率。

在給定X的情況下，可采用式(6)來計算X和Y之間的互信息：

I(X,Y)=H(Y)-H(Y|X)

(6)

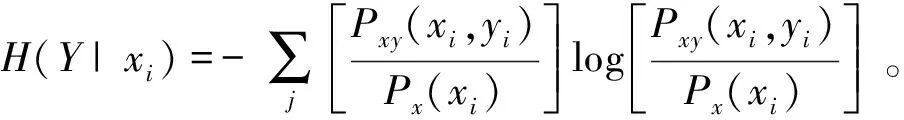
因此有：

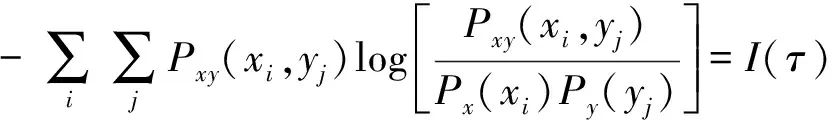
(7)

其中,Pxy(xi,yj)為事件xi和yi的聯合分布概率，I(τ)是與時間延遲τ有關的函數。I(τ)的大小代表了已知系統X，即x(t)在已知情況下，系統Y也就是y(t)的確定性大小。I(τ)=0，表示y(t)完全不可預測，即x(t)和y(t)完全不相關；而I(τ)的極小值則表示x(t)和y(t)最大可能的不相關，重構時使用I(τ)的第一個極小值對應的時間τ作為最優延遲時間。

在互信息的計算中，Fraser等[7]提出的互信息算法的具體過程是在x(橫軸)，y(縱軸)邊緣分布等概率的基礎上劃分網格。分段數可以通過經驗公式確定：

K=1.87(N-1)0.4

(8)

式中,N表示序列長度，K表示分段數。

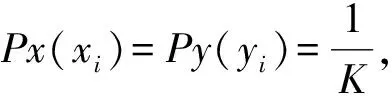
(9)

式中，n=1,2,…,Zm，R(n)分別對應某個網格(xi,yi)。

(2)偽近鄰法

偽近鄰法(False Nearest Neighbor，FNN)是確定嵌入維數最常用的方法，其主要思想是:如果m維重構相空間中的近鄰點在m+1維空間中仍然是近鄰點,則該點稱作真近鄰點,否則稱為偽近鄰點。當重構維數m小于原吸引子的真實維數時會產生偽近鄰點；反之,偽近鄰點消失,吸引子被打開。在某個維數m0處,偽近鄰點百分比(False Nearest Neighbor Percent, FNNP)將驟然降至(或接近)0,且不再隨m增大而變化,這個驟變點處的m0值就是最小嵌入維數。

FNN法確定嵌入維數的步驟如下:

對于時間序列{x(1),x(2),x(3),…,x(N)},當延遲時間為τ,嵌入維數為m,則相空間中的任一點:

Xm(i)={x(i),x(i+τ),x(i+2τ),…,x(i+(m-1)τ)}

(10)

式中,i=1,2,3,…,N-(m-1)τ。

其最近鄰點:

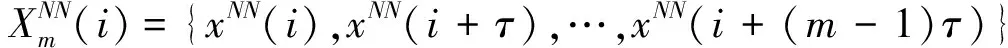
(11)

式中:j=1,2,3,…,N-(m-1)τ,且j≠i。

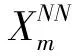
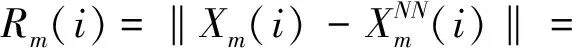
(12)

同理,當嵌入維數為m+1時,可得Rm+1(i)。可見:

現引入偽近鄰點的判據一:

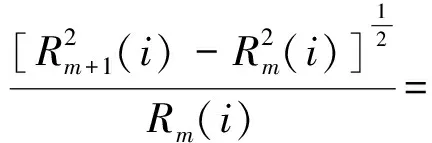
(14)

閾值Rtol可在[10,50]之間選取。對無限長精確的數據,用上述標準可獲得較好的結果。對有限長具噪聲的數據,補充判據二:

(15)

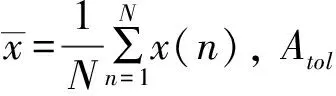
則對實測時間序列,m從2開始,計算虛假最近鄰點的比例,然后增加m,直到偽近鄰點的比例小于5%或偽近鄰點不再隨著m的增加而減少時, 可以認為完全打開,此時的m即為求得的最小嵌入維數[8]。

3.2 τ和m的聯合確定方法

Kim等[9]在實際計算中首次提出了關聯積分法(C-C算法)，該方法是一種能夠同時確定最佳時間延遲τ和最佳嵌入維數m的算法。關聯積分法主要是通過嵌入時間序列的關聯積分來構造統計量，該統計量代表非線性時間序列的相關性。

對于時間序列{x(t),t=1,2,…,N}，根據重構相空間中的相點：

y(i)={x(i),x(i+τ),…,x(i+(m-1)τ)}

(16)

則嵌入時間序列的關聯積分方程為:

(17)

式中：M=N-(m-1)τ，m是嵌入維數,N為原時間序列點數,τ是時間延遲,r是參考半徑,dij=‖y(ti)-y(tj)‖，θ(u)為Heaviside函數：

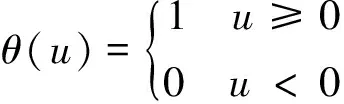
(18)

對于給定的任意閾值r，檢查相空間中點對之間的距離小于r的點對數量，它占所有點對總數的比例稱為關聯積分。對于時間序列{x(t),t=1,2,…,N}，將其分成τ個不相交的時間序列，τ為時間延遲，再由這τ個不相關的時間序列計算S(m,N,r,τ)。

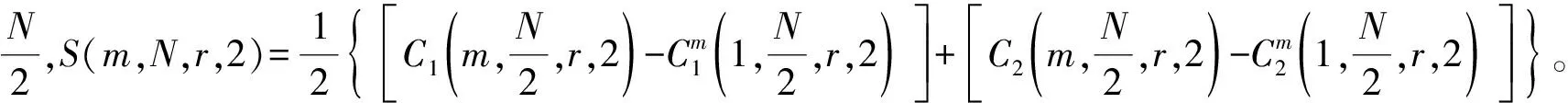
對于一般的自然數τ，將原時間序列分解成τ個不相交的時間子序列:{x(1),x(1+τ),x(1+2τ),…}，{x(2),x(2+τ),x(2+2τ),…}，…，{x(τ),x(2τ),x(3τ),…}，然后定義每個子序列的S(m,N,r,τ)為：

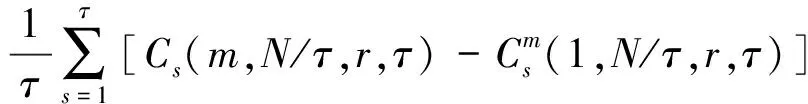
(19)

令N→∞有：

(20)

如果相空間中的點是獨立分布且N→∞，S(m,r,τ)對于所有的r將等于0，真實的數據序列是有限長度，且序列元素間可能相關，因此一般S(m,r,τ)≠0，從而局部最佳時間可確定為S(m,r,τ)的首次過零點或表現出對不同r變化最小點，這意味著點的分布最接近均勻分布。對于所有r定義變量為:

ΔS(m,τ)=max{S(m,rj,τ)}-min{S(m,rj,τ)}

(21)

Brock等[10]模擬研究了各種類型的分布后指出，對有限時間序列長度，當N≥500時，N,m,r的取值為一般地2≤m≤5，σ/2≤m≤2σ，(σ指時間序列的標準差)，可以通過有限序列對漸近分布作很好的近似。具體計算時，取m=2,3,4,5，ri=iσ/2,i=1,2,3,4。計算下列三個統計量:

(22)

(23)

(24)

m=int[(τw/τ)+1]

(25)

4 仿真與實驗驗證

4.1 仿真分析及對比

對于信號f(t)：

f(t)=sin(2*π*t)+sin(2*π*10*t)

(26)

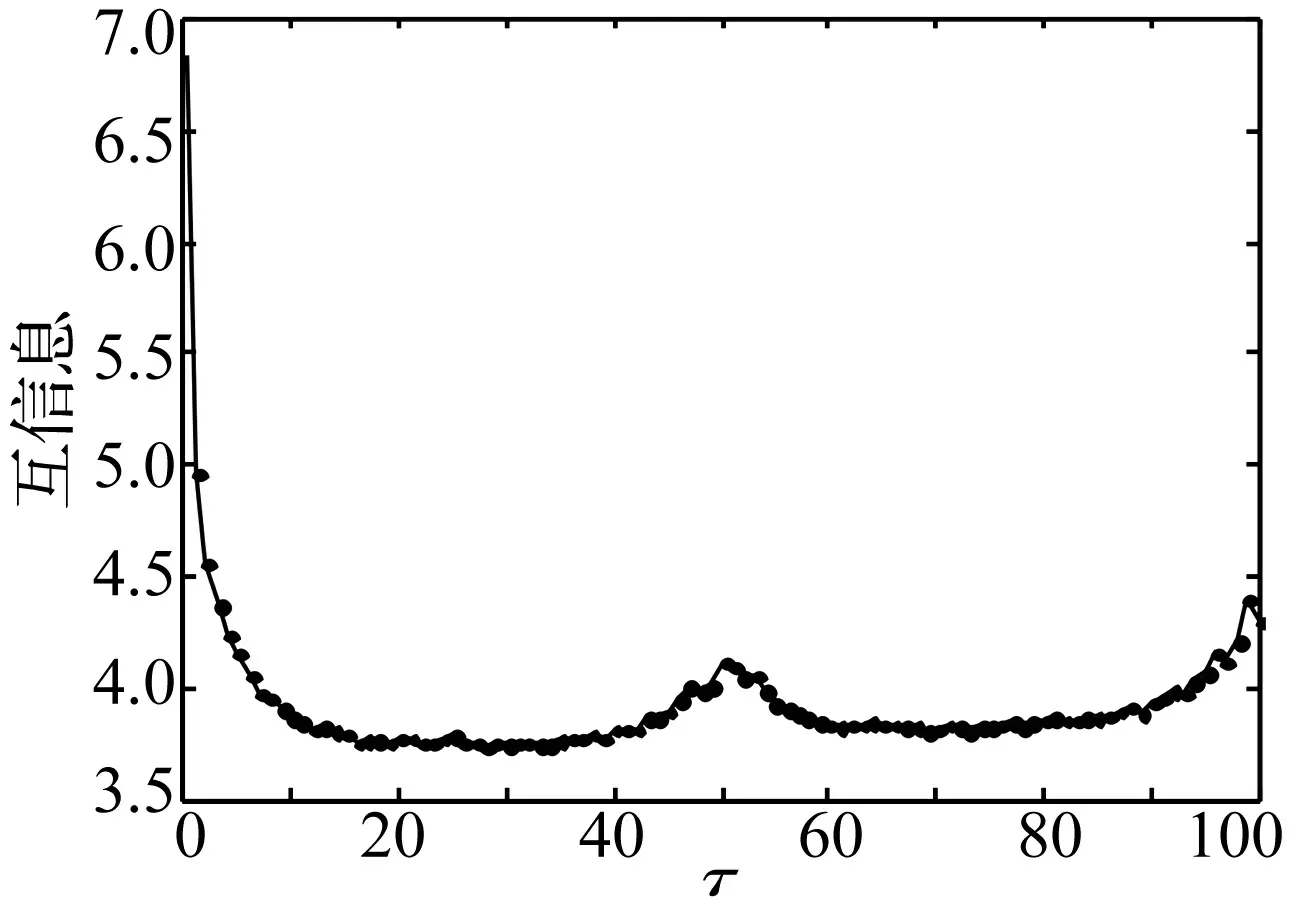
圖1 互信息隨時間延遲的變化曲線

信號在正常狀態下包含2個頻率成分，對于該狀態下的時間序列可采用前文所述的兩種不同的觀點對應的方法來確定模型參數。首先采用1 000 Hz的采樣頻率對信號進行離散化，選擇重構時間序列長度為1 024點，利用互信息法計算時間序列的時間延遲τ與互信息之間的關系，如圖1所示。按照互信息法確定延遲時間的原則，可知時間延遲τ=12。

圖2是給出了基于FNN法計算偽近鄰率隨嵌入維數的變化關系曲線。判據一的閾值Rtol選擇為15，判據二的閾值Atol選擇為2，綜合兩種判據的效果，可以計算其聯合判據曲線，如圖2中紅色圓圈連線所示。

為了驗證所得的算法參數對異常檢測的效果，在原始信號f(t)中增加一個頻率為20 Hz的正弦分量，以此模擬信號發生了異常，發生時刻為60 s，從而構成帶有異常變化的信號f′(t)，如式(27)所示。

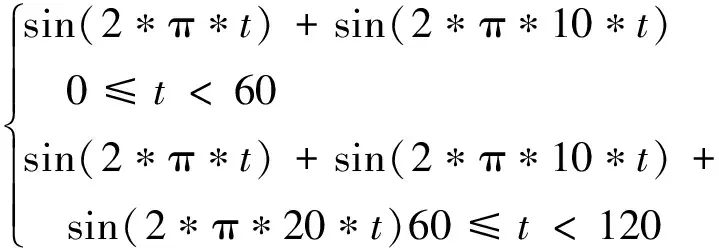
(27)

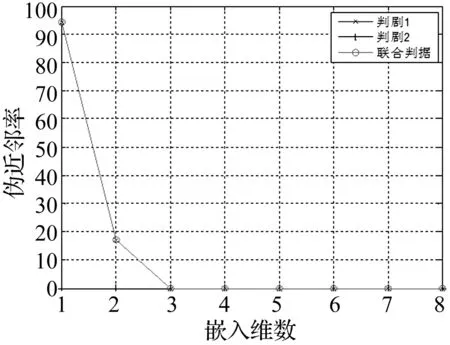
圖2 偽近鄰率隨嵌入維數的變化曲線

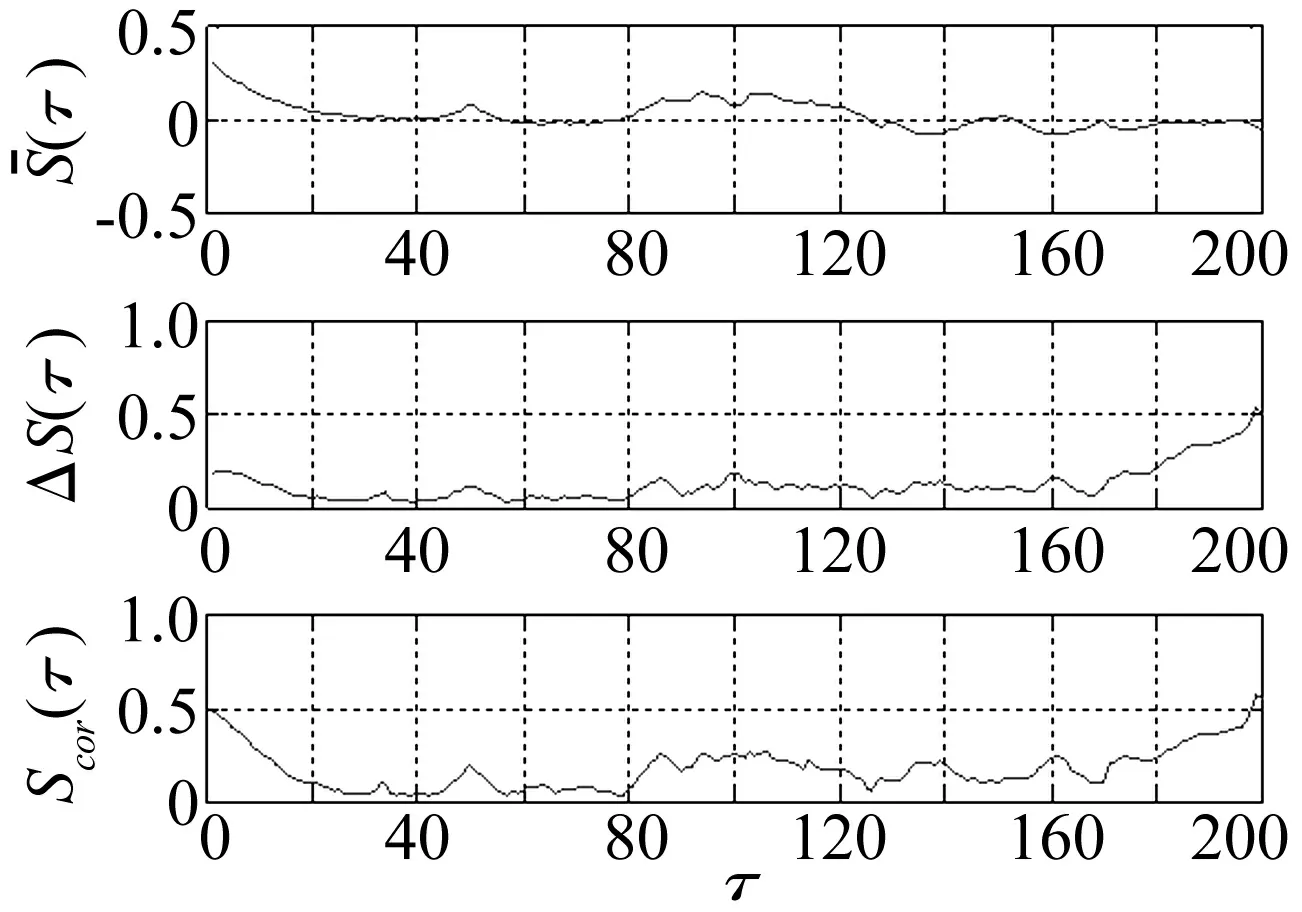
圖和Scor(τ)的變化曲線

圖4 模擬異常信號f′(t)

選擇采樣頻率1 000 Hz，對信號進行離散化，異常信號f′(t)的時域波形如圖4所示，將前文中基于f(t)信號所確定的模型參數延遲時間和嵌入維數作為排列熵的模型參數，相鄰兩個重構時間序列之間沒有數據重疊，依次計算該異常信號的排列熵，結果如圖5所示。點的連線代表采用參數獨立確定方法對應的排列熵值隨時間的變化曲線，圓圈連線代表采用參數聯合確定方法對應的排列熵值隨時間的變化曲線。對比兩條曲線的變化特點可知，前者要優于后者，一是前者曲線跳變更加明顯，即異常敏感性更高；二是前者曲線在非異常區域內波動更小，即穩態平穩性更好。由此可見，排列熵模型中參數的獨立確定法能夠獲得更好的異常檢測效果。

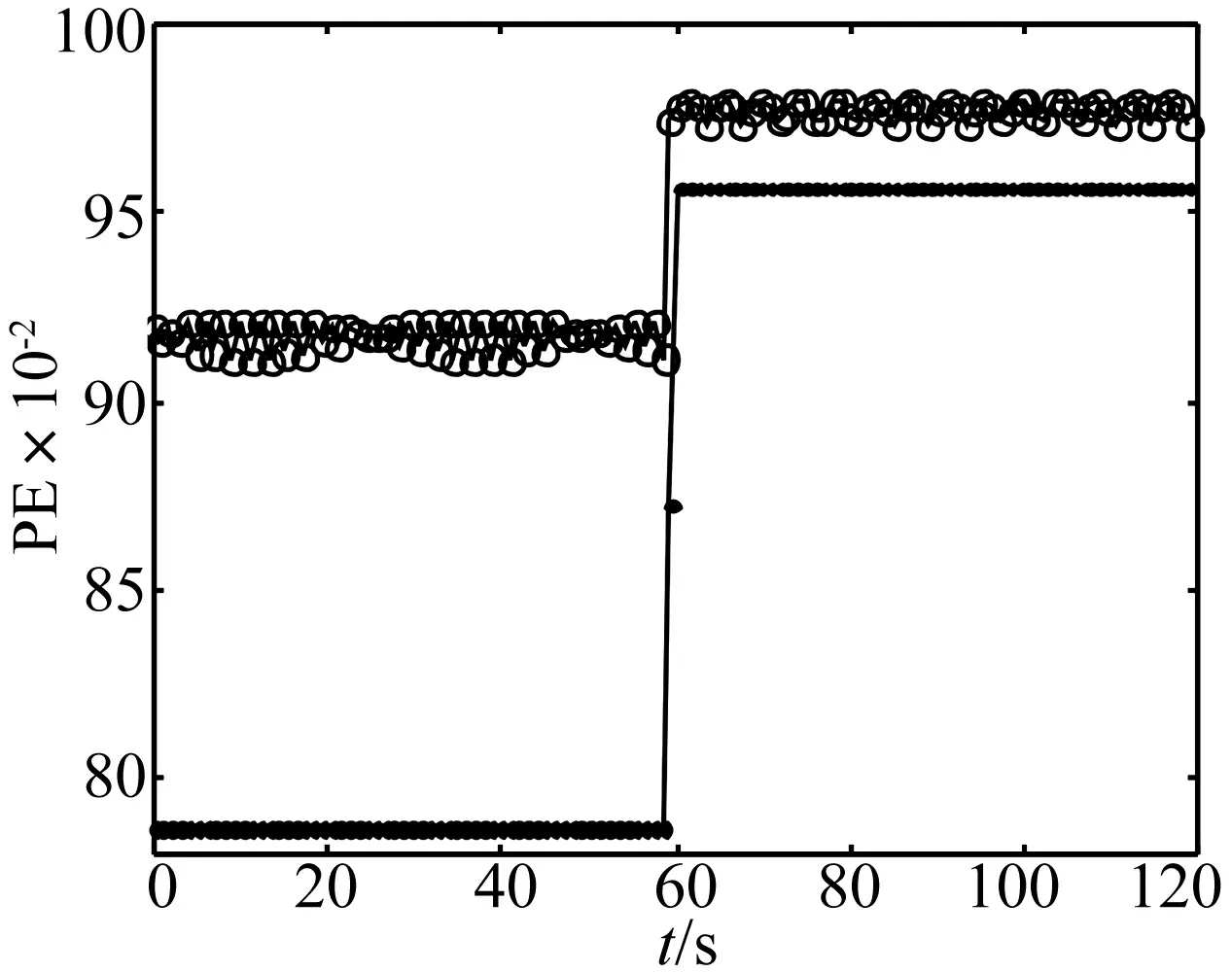
圖5 排列熵異常檢測結果

4.2 軸承異常檢測

為了進一步檢驗方法的有效性，提出對軸承試驗臺全壽命振動信號數據[11]進行異常檢測，數據來自美國NSFI/UCR的智能維護系統中心(IMS)，本文采用了該試驗第2輪次的測試數據。

由于EMD方法具有自適應分解特性，比較適用于非線性、非平穩的信號分析，在此采用EMD方法對振動信號進行預處理。該實驗是軸承外圈發生故障，異常信息主要集中在高頻部分，因此對分解后的IMF1分量利用參數優化方法確定排列熵模型參數，最后利用排列熵算法對軸承振動信號EMD分解后的IMF1分量進行異常檢測。

(1)模型參數的確定

選擇軸承在正常狀態下的振動信號數據，長度為1024，經EMD分解后選擇IMF1分量，計算其延遲時間與互信息的關系。當τ=1時互信息第一次取得極小值，故取延遲時間τ=1。然后基于FNN方法計算偽近鄰率和嵌入維數之間的關系，因此可確定m=4。

(2)排列熵異常檢測

對于實驗中每組數據，將其分為20段，每段長度為1024，各段之間沒有數據重疊，對每段進行EMD分解，計算IMF1分量的排列熵值，然后取其平均值作為一組數據的特征值，依次計算各組數據的排列熵值。兩種不同方法確定模型參數后得出的結果如圖6所示，橫坐標是每組數據對應的測試時間，縱坐標表示排列熵結果，其中圖6中曲線(a)表示聯合確定算法參數后排列熵的計算結果變化曲線，圖6中曲線(b)表示獨立確定算法參數后排列熵變化曲線。圖7是任意選定算法參數后得出的排列熵計算結果，

顯然，經過參數優化后的模型輸出結果更好，主要表現在：一是異常表現效果更明顯；二是檢測異常的發生時間要更早。對于不同方法優化參數的異常檢測結果可知，兩者預測趨勢基本相同。在異常起始點處，圖6中曲線(b)異常跳變更明顯；在異常區域內，排列熵均經歷了先減小而后逐漸穩定的過程，但曲線(b)排列熵值變化要快，排列熵最小值與正常狀態之間的差值要大于0.04，而圖6中曲線(a)不到0.03，因此說明模型參數τ=1m=4對于異常檢測更敏感，檢測效果更明顯；圖中故障起始點均發生在同一時刻，排列熵值下降到最低點時刻也相同，但曲線(a)故障跳變要更明顯，并且此后，其排列熵值變化要快，說明參數τ=4m=4對于故障發生后檢測更敏感，檢測效果更明顯。因此，關于τ和m的選取，兩種確定參數的方法都具有可行性，但對于異常檢測來說，算法參數的獨立確定方法更有效。

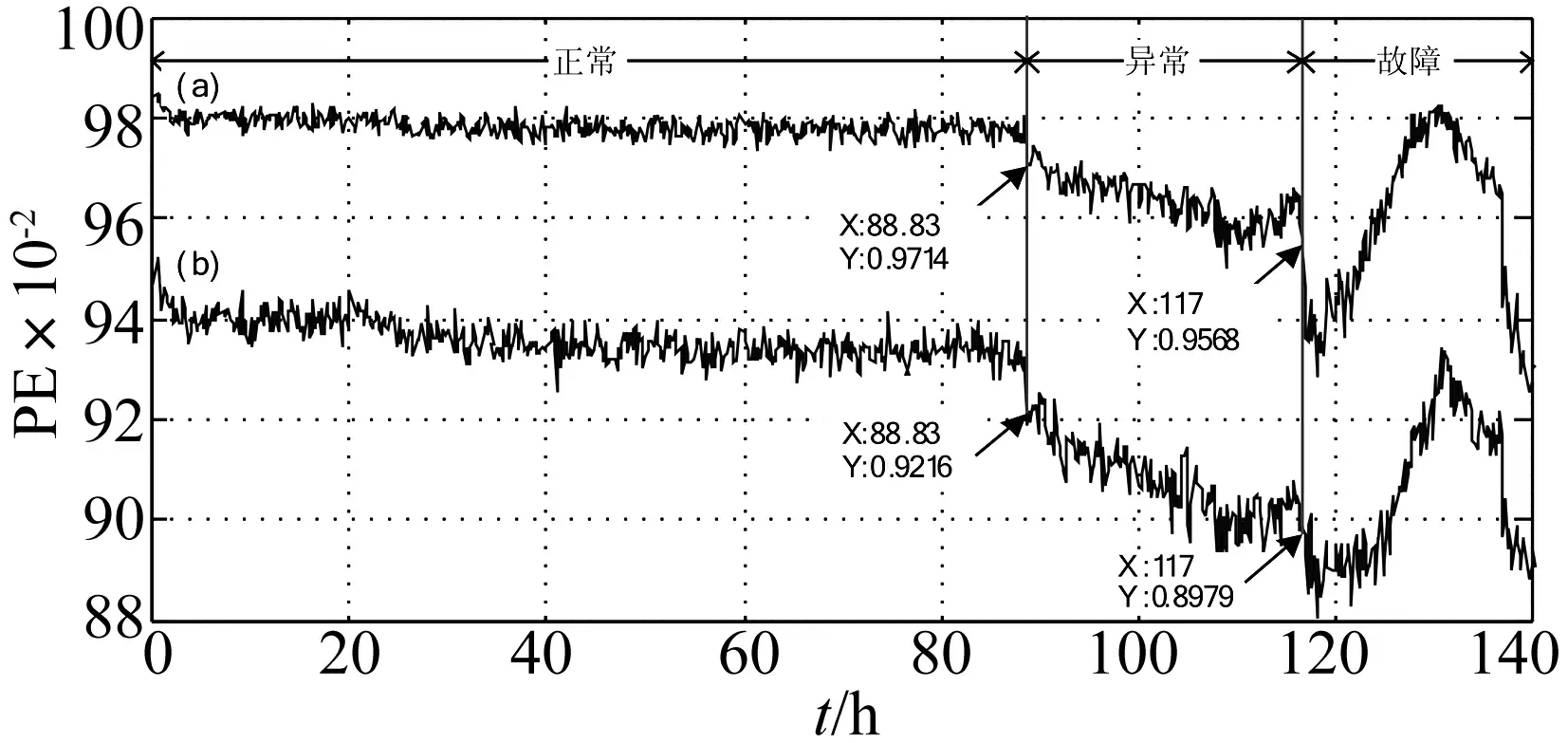
圖6 排列熵計算結果變化曲線

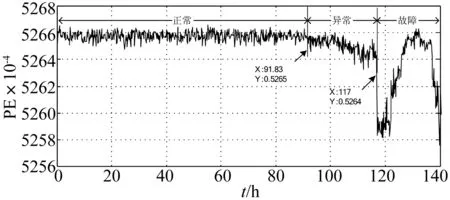
圖7 τ=22，m=9時排列熵變化曲線

5 結 論

本文重點研究排列熵算法參數的優化確定方法，根據模型的基本原理，提出以重構時間序列最佳相空間的方法確定模型參數，克服了以往對排列熵參數人為主觀或憑經驗選擇的不確定性。根據當前相空間重構的兩種不同觀點，介紹了不同觀點中比較典型算法的基本原理，利用仿真信號和滾動軸承全壽命周期數據直觀地說明了不同確定方法對異常檢測效果的影響，結果表明模型參數的獨立確定要優于聯合確定方法，為排列熵算法在不同領域推廣應用時，如何確定算法的最佳參數奠定了基礎。

參 考 文 獻

[1]Cao Y H, Tung W W, Gao J B,et al. Detecting dynamical changes in time series using the permutation entropy[J].Phys RevE,2004,70(4)：1-7.

[2]Nicolaou N, Georgiou J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines[J]. Expert Systems with Applications,2012,39(1)：202-209.

[3]Nair U, Krishna B M, Namboothiriet V N M. Permutation entropy based real-time chatter detection using audio signal in turning process[J]. International Journal of Advanced Manufacturing Technology, 201046:161-68.

[4]侯 威,封國林,董文杰.利用排列熵檢測近40年華北地區氣溫突變的研究[J].物理學報,2006,55(5):2663-2668.

HOU Wei, FENG Guo-ling, DONG Wen-jie. A technique for distinguishing dynamical species in the temperature time series of north china[J]. Acta Physica Sinica,2006,55(5):2663-2668.

[5]劉永斌, 龍 潛, 馮志華, 等. 一種非平穩、非線性振動信號檢測方法的研究[J]. 振動與沖擊, 2007, 26(12)：131-134.

LIU Yong-bin, LONG Qian, FENG Zhi-hua, et al. Detection method for nonlinear and non-stationary signals[J]. Journal of Vibration and Shock, 2007, 26(12)：131-134.

[6]謝忠玉,張 立.相空間重構參數選擇方法的研究[J].中國科技信息2009(16):42-43.

XIE Zhong-yu, ZHANG Li. Selection of embedding parameters in phase space reconstruction[J]. China Science and Technology Information,2009(16):42-43.

[7]Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information [J]. Phys Rev A, 1986, 33(2):1134-1140．

[8]Kennel M B, Brown R, Abarbanel H D I. Determining embedding dimension for phase-space reconstruction using a geometrical construction[J]. Physical Review A, 1992, 45(6)：3403-3411.

[9]Kim H S,Eykholt R, Salas J D. Nonlinear dynamics, delaytimes and embedding windows [J]. Physica D, 1999, 127(1):48-60.

[10]Brock W A, Hsieh D D A,Lebaron B D al. Statistical theory and economic evidence[M]. M IT Press, Cambridge, MA, 1991.

[11]Feng F Z, Zhu D D, Jiang P C, et al. GA-SVR based bearing condition degradation prediction[J].Key Engineering Material2009413-414431.