基于LMI的旋轉起重機魯棒控制器設計

歐陽慧珉， 佐野滋則， 內山直樹， 張廣明， 王德明， 梅 磊

(1. 南京工業大學 自動化與電氣工程學院,南京 211816；2. 日本豐橋技術科學大學 機械工程系,豐橋 441-8580)

起重機系統被廣泛地應用于各種工業場所，例如建筑工地，港口，鐵路站場以及其他地方。起重機應該實現迅速地運輸荷載到指定的位置而不產生多余的擺動。然而，旋臂的旋轉運動會使荷載產生一個二維擺角；因此，操作人員必須具備很高的熟練度來控制起重機使得荷載迅速而準確地到達指定位置。操作上的失誤會造成事故，人員傷亡以及破壞周圍的環境。

為了減輕操作人員的負擔以及提高他們工作的安全性，許多研究人員已經為起重機系統開發了各種各樣的控制方式。這些方法主要可以分為兩種類型：一種是閉環控制，即利用由傳感器系統測量到的擺角信息實現消擺控制。Nakazono等[1-2]提出了一種基于遺傳算法的神經網路控制器來實現起重機的消擺控制。曹玲芝等[3]針對橋式起重機的小車定位和負載擺動控制問題提出了一種模糊滑模控制方法。另一種是開環控制，即不需要擺角信息的軌道生成法。Terashima等[4-5]提出了一種基于坐標變換的旋轉起重機直線搬送最優控制方法。Maleki等[6]提出了一種輸入整形控制法實現起重機的消擺控制。在上述兩類控制方式中，前者可以實現對起重機系統的魯棒控制，相反，后者一般只適合于不考慮外部干擾的理想系統，它們很難實現較好的戶外性能。因此，閉環控制方式常常被應用到實際的起重機控制系統中。

然而，在現存的大多數研究中沒有對控制器關于懸繩長度變化的魯棒性解析[1-6]。如果在設計控制系統時考慮到繩長變化所帶來的影響，就可以容易地操作起重機且無需測量繩長的傳感器系統，從而大大地簡化起重機結構和降低其安裝成本。本研究的目的就在于提出一種魯棒控制方法來解決上述問題。

由于所設計的控制系統對于如關節間摩擦，荷載質量以及旋臂的轉速等參數的變化必需具有魯棒性，因此首先基于干擾觀測器導出起重機的線性模型。其次，設計一個含有積分器的狀態反饋控制器從而實現在給定繩長變化范圍的情況下的魯棒控制。所提出的控制系統滿足閉環極點配置和最優化控制的約束條件。這些條件可以用線性矩陣不等式(LMI)表示[7]，而控制器增益則可由LMI最優化算法求出。最后，比較仿真和實驗結果驗證所提方法的有效性。

1 旋轉起重機模型

在如圖1所示的旋轉起重機模型中，θ1,θ2分別表示旋臂起伏運動平面的擺角和旋轉運動平面的切線方向的擺角；θ3,θ4分別表示旋臂的起伏角和旋轉角；L,l分別表示旋臂長度和懸繩長度；x,y,z表示荷載的三維空間位置。

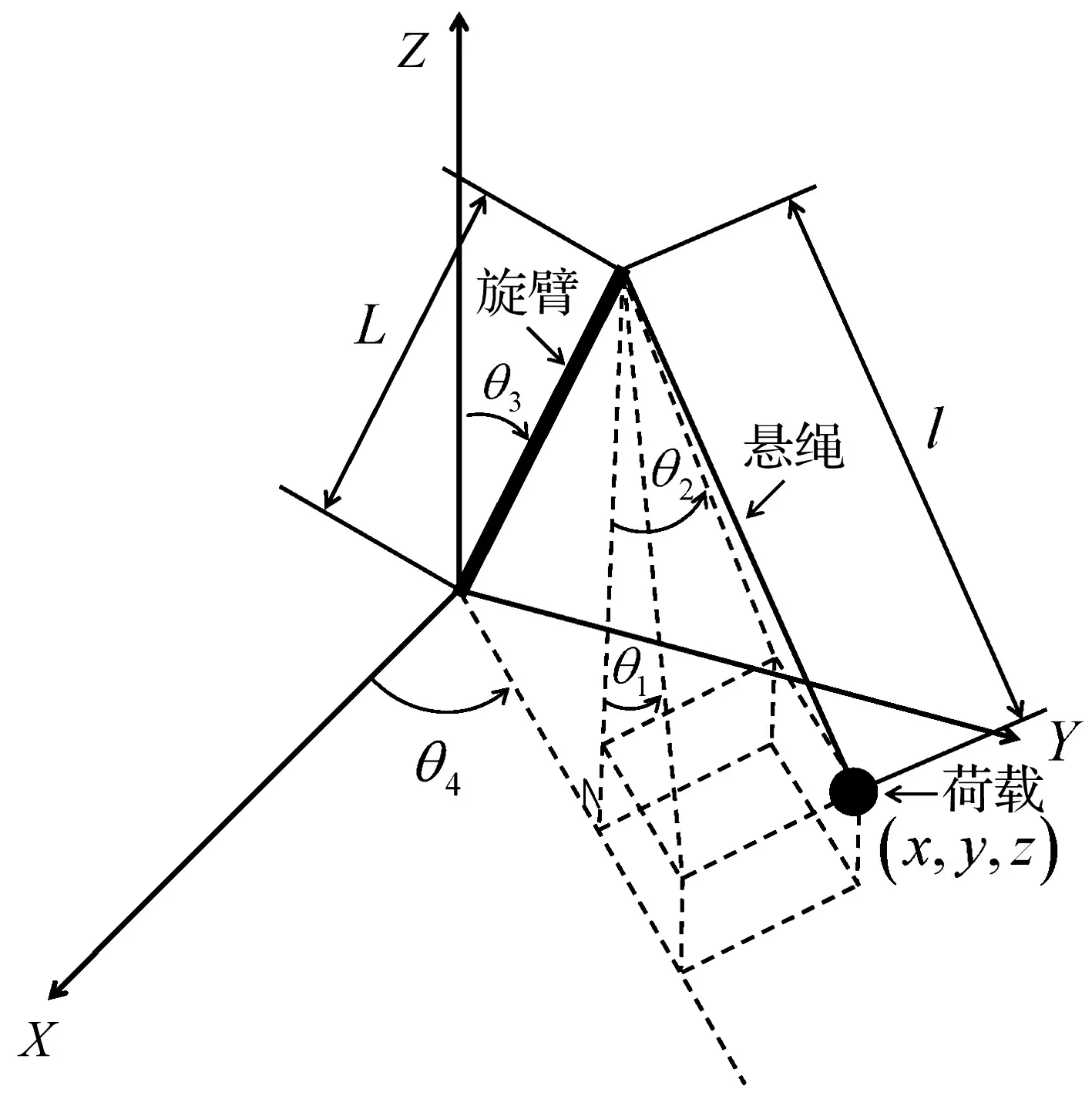
圖1 旋轉起重機模型

假設旋轉起重機模型具有以下特性：

(1)荷載可以看作是一個質點，且懸繩的扭力可以忽略不計。

(2)旋臂的起伏角和旋轉角以及它們的角速度；兩個方向的擺角以及它們的角速度都可測量。

(3)由于擺角θi很小，因此sinθi=θi和cosθi=1 (i=1,2)成立。

旋臂的起伏運動和旋轉運動可由下式表示：

(1)

式中:Ji+2,di+2,Ki+2,ui+2分別表示旋臂轉動慣量，包含非線性力的系統外部干擾，系統參數以及指令電壓。式(1)假設旋臂轉動慣量Ji+2是常量，其變化部分可看作是系統外部干擾并包含于di+2。

為了補償系統外部干擾的影響，將以下所示干擾觀測器(DOB)應用于式(1)：

(2)

式中:s,vi+2,ωi+2分別表示微分算子，由反饋控制器算出的新控制輸入以及低通濾波器(LPF)的截止角頻率。該控制系統的方框圖如圖2所示。起重機系統動力學特性在低頻區域可表示為下式：

(3)

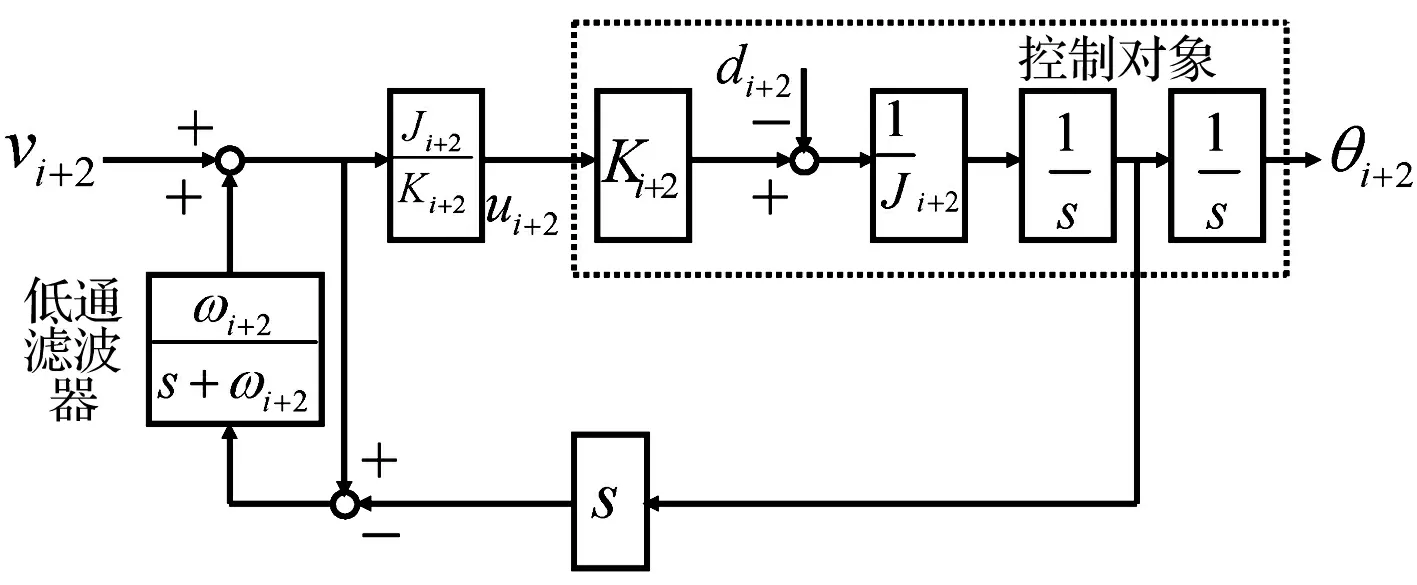
圖2 含有干擾觀測器控制系統

另一方面，根據拉格朗日運動方程懸繩和荷載組成的振動系統的動力學方程可由下式表示：

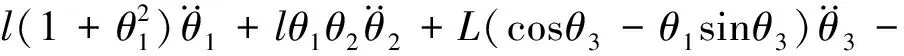
(4)

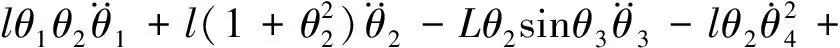
(5)

式中:g表示重力加速度。

起重機系統變量及其時間導數分別如下所示：

(6)

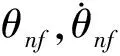
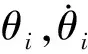
在這種情況下，起重機線性模型如下所示：

(7)

式中:ξ=g/l,γ1=Lsinθ3f/l,γ2=Lcosθ3f/l。

2 魯棒控制器設計

本節提出一種基于LMI的控制器來實現對給定繩長變化范圍的魯棒控制。

2.1 穩定范圍的LMI表現

(8)

式中:θ,α,β都是正實數，X是對稱矩陣。

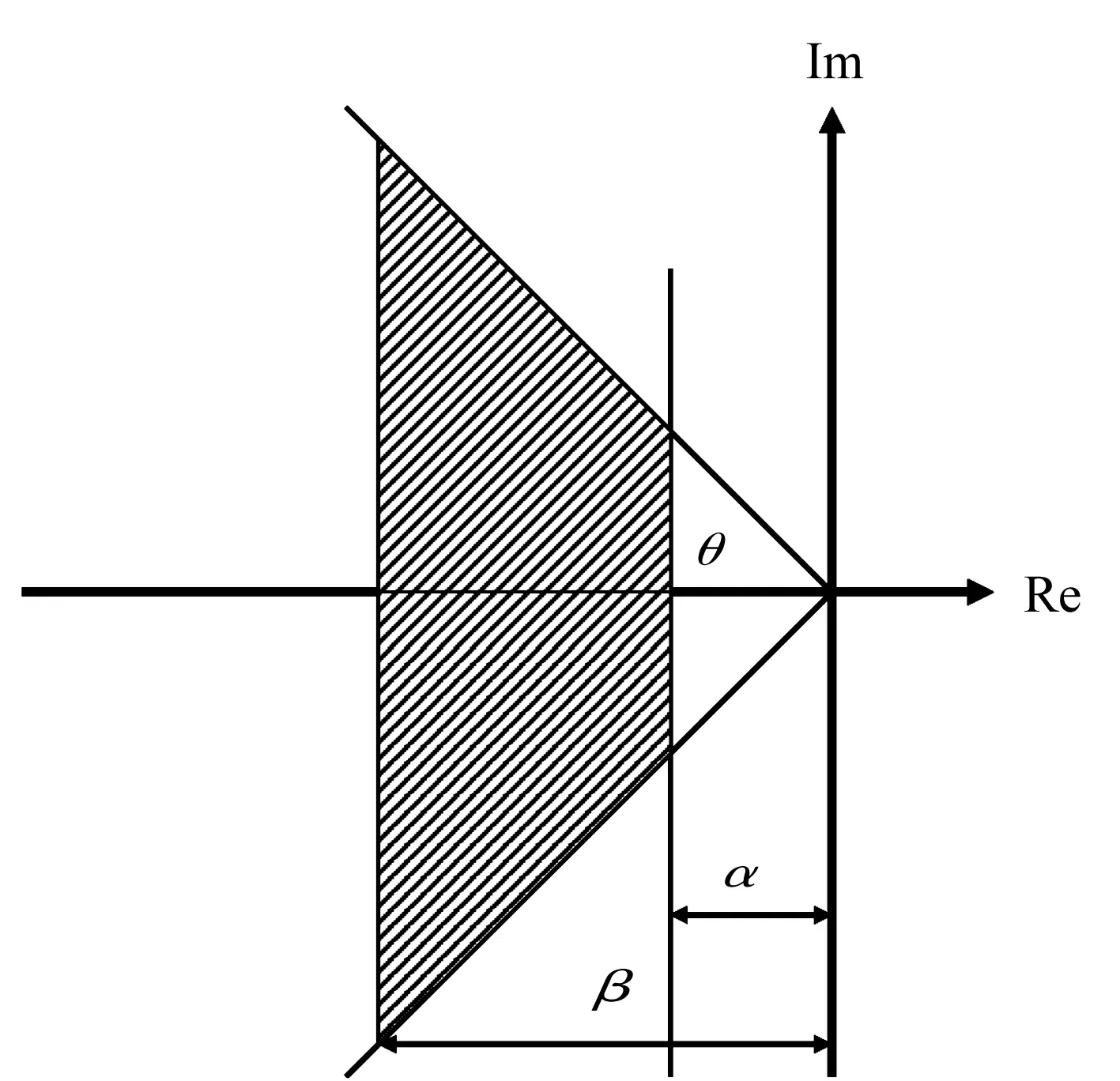
圖3 穩定區域

2.2 含有積分器的狀態反饋控制器

考慮如下含有積分器的起重機線性控制系統：

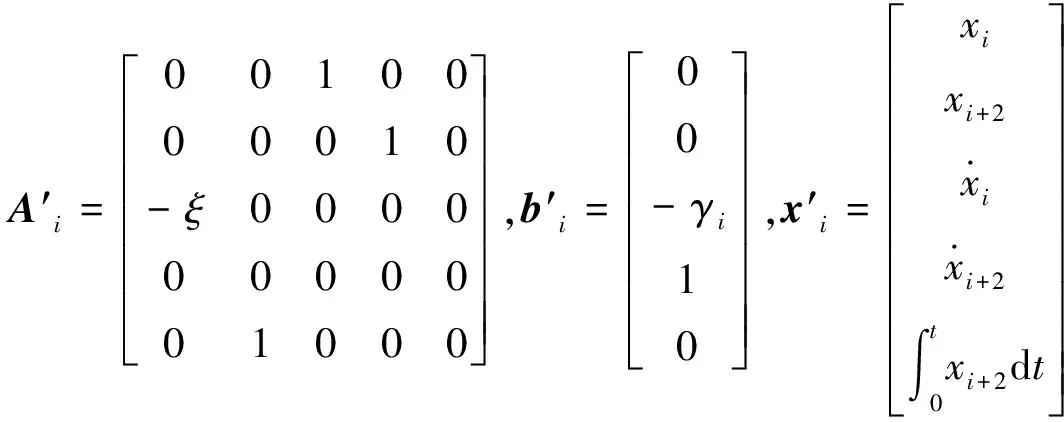
(9)

由此可得到閉環控制系統如下所示：

(10)

其控制器增益可由極點配置法和最優化算法求得。

2.3 極點配置問題的LMI表現

本小節將基于LMI對極點配置問題進行公式化。如果式(10)所示系統的全部極點都配置在圖3所示區域，那么該系統就穩定。因此，本問題可以轉化為尋找合適的X,Mi使得以下的方程成立：

(11)

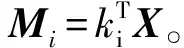
2.4 最優化問題的LMI表現

考慮以下變量和性能指標J[7]：

(12)

(13)

2.5 控制器設計

將上述兩個問題結合起來設計控制器。

令X=X2,Mi=Mi2，可得：

(15)

(16)

上述問題可由LMI最優化算法求解[8]。

2.6 魯棒性分析

本小節將驗證如果式(10)所示系統在所給繩長變化范圍的兩端能滿足2.3節中所述極點配置的條件，那么對于在該范圍內任意繩長來說該系統都能滿足所給條件。

假設繩長變化范圍是l∈[l1,l2]，可得：

(17)

式中:φ1+φ2=1,φ1,φ2>0。

此時，式(10)所示系統可表示為下式：

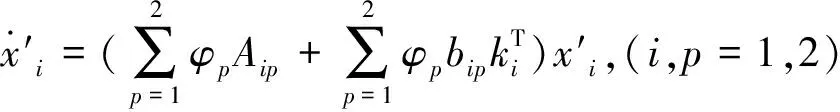
(18)

式中:ξi=g/li,γi1=Lsinθ3f/l1,γi2=Lcosθ3f/l2。

因此，式(11)所示條件可表示為下式：

(19)

(20)

3 仿真與實驗

3.1 目標軌道

為了驗證本文中所提方法的有效性，使用如下所示初始和最終位置的加速度都為零且廣泛地應用于各種工業場合的擺線作為起伏角和旋轉角的目標軌道。

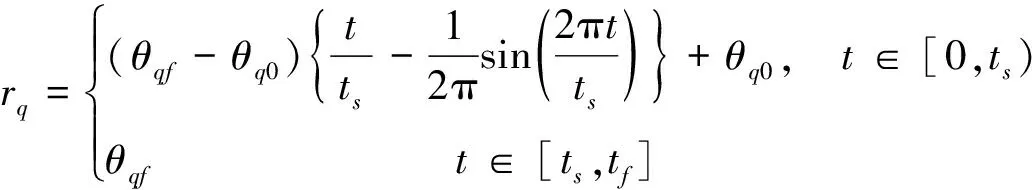
(21)

式中:θq0,θqf,ts,tf分別表示初始角度，最終角度，調節時間，終了時間。在本文中，各參數分別設定為θ30=30° ,θ3f=50°,θ40=0°,θ4f=45°,ts=3 s,tf=10 s。

3.2 仿真與實驗條件

由于式(10)所示閉合系統可以近似看成一個2次系統，而對于位置控制而言，該2次系統的阻尼系數ζ一般可設計在0.2～0.4之間[9]，因此參數θ可根據θ=cos-1ζ求得。又因為調節時間ts=3 s，所以固有角頻率ωn可根據文獻[9]求得。因此，參數α,β=ζωn。在本研究中，圖3所示穩定區域各參數θ=78°,α=1,β=30；再應用試湊法設定Qi=diag{1 500,315,1 500,315,50},Ri=1。控制器增益由LMI最優化算法求出并如下所示：

(22)

3.3 干擾抑制

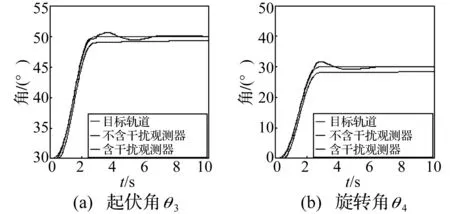
圖4 干擾觀測器對關節摩擦抑制效果

本小節通過仿真來驗證干擾觀測器對關節摩擦，荷載質量以及旋臂旋轉速度等參數變化的魯棒性。首先，考慮關節摩擦對系統的影響，其仿真結果如圖4所示，其中起伏角θ3和旋轉角θ4的定常誤差都得到很好的改善。其次，考慮荷載質量變化對系統的影響，其結果如圖5所示。在該仿真中，不考慮關節摩擦的影響。同樣起伏角θ3和旋轉角θ4的跟蹤特性沒有因為荷載質量大幅地變化而變化。最后，考慮旋臂旋轉速度變化對系統的影響，其結果如圖6和圖7所示，并得到了與圖5大致相同的結果。

3.4 比較仿真

本小節通過比較仿真來驗證新方法的有效性。在該仿真中，對于特定的系統(即l=0.5 m時作為公稱模型)，其控制器仍然采用含有積分器的狀態反饋控制，只是控制器增益由基于主極點的極點配置方法求得。由于該系統可以近似地看為一個2次系統，根據最優阻尼系數理論，設定該系統的主極點為-1.5±j1.5(1/s)，而非主極點則盡量以不影響控制性能，即其實部

為主極點實部的6倍以上，為原則設定為-10±j1.5(1/s),-10(1/s)。此時所得控制器增益如下所示：

(23)

其仿真結果如圖8所示。然后，在不改變控制器增益的情況下，繩長l分別為0.25 m和0.75 m時的結果如圖9和圖10所示。雖然圖8和圖10都得到很好的旋臂跟蹤特性以及擺角抑制特性，但是當繩長l為0.25 m時該控制系統則變成了不穩定系統。

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

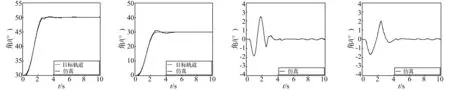
(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

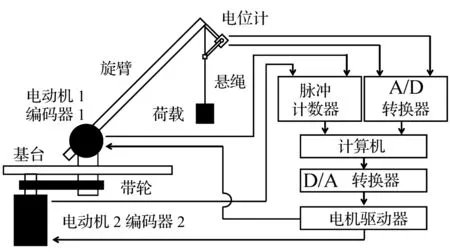
圖11 實驗系統

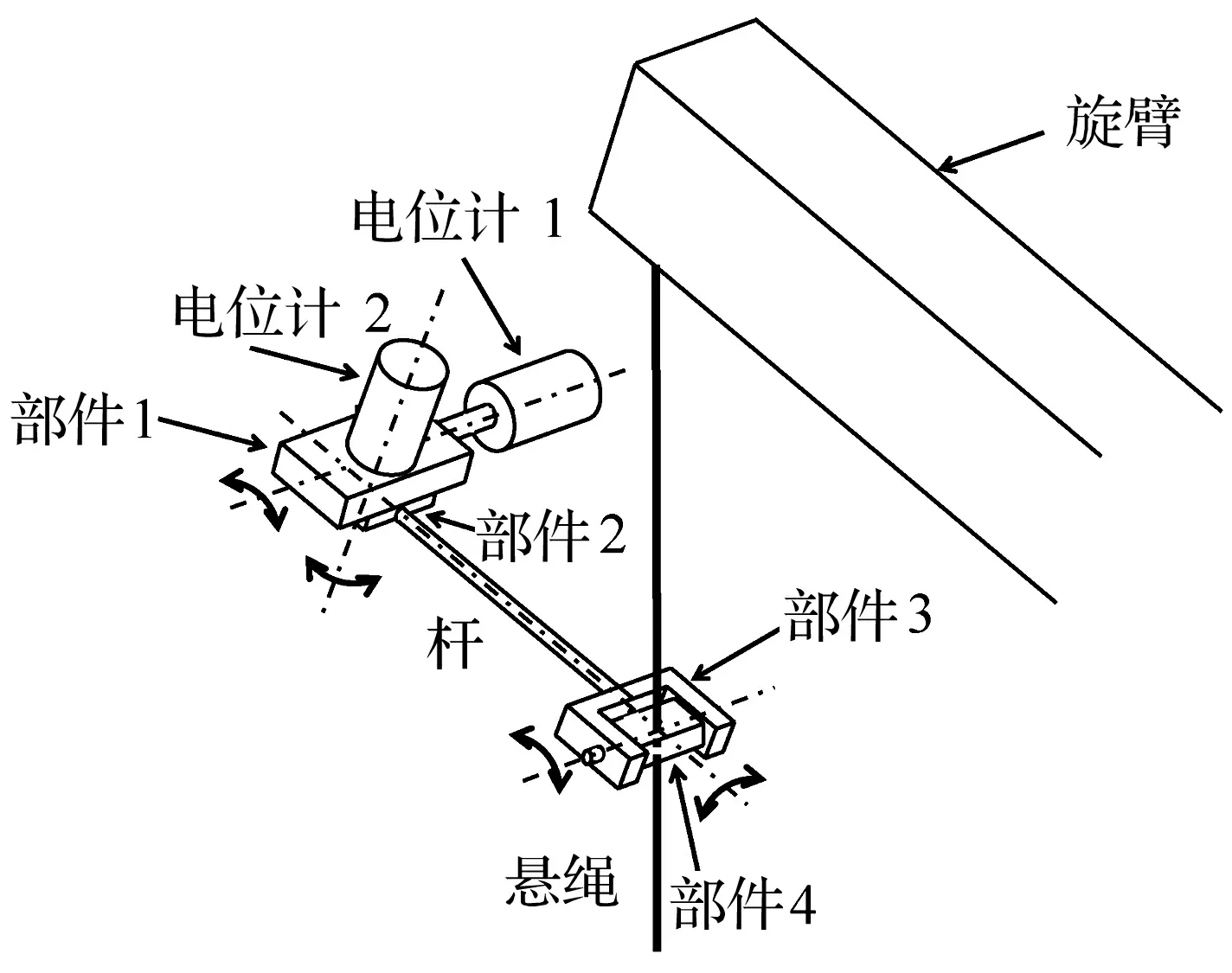
圖12 測量擺角的傳感器系統

3.5 實驗系統

如圖11所示的系統由驅動旋臂起伏和旋轉運動的兩個同樣規格的直流電動機，旋臂，懸繩，荷載以及測量擺角的電位計等部分構成。起伏角和旋轉角可由旋轉編碼器測得，其角度測量分辨率為1.8×10-3deg。

測量擺角的傳感器系統如圖12所示。測量起伏方向擺角θ1的電位計1固定在旋臂上。測量旋轉方向擺角θ2的電位計2固定在部件1上，并圍繞電位計1的旋轉軸旋轉。部件2和長桿共同圍繞電位計2的旋轉軸旋轉。部件3相對于長桿，部件4相對于部件3分別旋轉。部件4可沿著懸繩滑動。其角度測量分辨率為6.4×10-2deg。

表1 起重機參數

另外，該實驗系統的各主要參數如表1所示。其中Ji+2,Ki+2(i=1,2)由電機特性測試實驗所得；L,m為硬件設計參數；l1,l2由直尺測量所得。

3.6 實驗驗證

本小節通過實驗來驗證新方法的有效性，設繩長l分別為0.25 m,0.5 m,0.75 m，其結果如圖13～圖15所示。雖然在圖13(a)～圖15(a)和圖13(b)～ 圖15(b)中存在一點超調，但是在圖13(c)～圖15(c)和圖13(d)～圖15(d)中的擺角都得到很好的抑制，并且實驗結果與仿真結果基本保持一致。

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

(a) 起伏角θ3 (b) 旋轉角θ4 (c) 擺角θ1 (d) 擺角θ2

4 結 論

本文為了實現起重機系統關于繩長變化的魯棒控制，首先基于干擾觀測器導出了起重機的線性模型。然后，提出了含有積分器的狀態反饋控制器，其增益通過LMI最優算法求解極點配置和最優化問題得出。該方法的優點在于，當給定繩長變化范圍時，只需要解析在該范圍兩端的特性就能保證其對于整體的魯棒性，大大降低了控制器設計的難度。最后通過比較仿真以及實驗驗證了該方法的有效性。

然而，在該方法中同時使用了旋臂的起伏運動和旋轉運動來控制擺角。實際上，旋臂的起伏運動是用來對抗重力的，因此從節能和安全的觀點出發，將提出只利用旋臂旋轉運動實現擺角抑制控制的方法。

參 考 文 獻

[1]Nakazono K, Ohnishi K, Kinjo H, et al. Vibration control of load for rotary crane system using neural network with GA-based training [J]. Artificial Life and Robotics, 2008, 13：98-101.

[2]Nakazono K, Ohnishi K, Kinjo H, et al. Load swing suppression for rotary crane system using direct gradient descent controller optimized by genetic algorithm [J]. Transactions of the Institute of Systems, Control and Information Engineers, 2011, 22(8)：303-310.

[3]曹玲芝, 劉 磊, 張曉峰. 橋式起重機水平運動系統的模糊滑模控制[J]. 電氣傳動, 2011, 41(6)：47-50.

CAO Ling-zhi, LIU Lei, ZHANG Xiao-feng. Fuzzy sliding mode control for horizontal moving process of overhead cranes [J]. Electric Drive, 2011, 41(6)：47-50.

[4]Terashima K, Shen Y, Yano K. Modeling and optimal control of a rotary crane using the straight transformation method [J]. Control Engineering Practice, 2007, 15(9)：1179-1192.

[5]沈 瀅, 曹金城, 王 玲. 旋轉起重機建模及負載擺動最優控制[J]. 沈陽建筑大學學報(自然科學版), 2009, 25(3)：605-608.

SHEN Ying, CAO Jin-cheng, WANG Ling. Modeling of a rotary crane and the optimal control for load swing [J]. Journal of Shenyang Jianzhu University (Natural Science), 2009, 25(3)：605-608.

[6]Maleki E, Singhose W. Dynamics and control of a small-scale boom crane [J]. ASME Journal of Computational and Nonlinear Dynamics, 2011, 6(3):1-8.

[7]Chilali M, Gahinet P.H∞design with pole placement constraints：an LMI approach [J]. IEEE Transactions on Automatic Control, 1996, 41(3)：358-367.

[8]Gahinet P, Nemirovski A, Laub AJ, et al. LMI control toolbox for use with MATLAB [M]. 1995.

[9]Takagi S. Control engineering for mechatronics (In Japanese)[M]. 1992.