高精度模糊控制器在水輪機調節中的應用
曹 歡, 楊 棣
(中國長江電力股份有限公司三峽水力發電廠,湖北 宜昌 443000)
0 引 言
水輪機調節系統是一個高度非線性的、時變的復雜控制系統,系統內含有時滯、轉速死區,而且還呈現出非最小相位特性。盡管現在的微機調節器多種多樣,但就其調節規律而言,多為傳統的PID,真正的高級控制策略目前還在研究和試驗階段。之前很多學者將模糊控制理論用于水輪機調節控制中[3-4],其調節規律有著明顯的改善,減小了系統的超調量,增加了系統的穩定性。模糊控制是一種專家系統,他需要工作人員在長期工作中積累的經驗,并實現了數學表達。然而,在利用模糊控制理論的時候,其論域很難確定,往往要花很長時間對其調試,才能達到較好的論域值,且該論域值在試驗中不能進行調整,無法實現自適應的要求,針對此問題,我們設計了一類基于變論域的高精度模糊控制器[5-6],它是在模糊PID控制基礎上對原有的模糊控制進行了改進與優化,使模糊控制器在微偏差范圍內也能保證精度的要求,且不改變其粗調快速的優點。
1 控制器設計
1.1 PID控制器
PID器也稱為比例-積分-微分控制器,已有70多年的應用歷史,作為最早實用化的工業控制器到現在依然有著最廣泛的應用。PID控制器算法簡單,對于連續PID算法有:
(1)
(2)
(3)
公式(2)減去(3),經過化簡可得增量式數字PID算式:
△Dy(n)=Dy(n)-Dy(n-1)=Kp[e(n)-e(n-1)]+Kie(n)+Kd[e(n)-2e(n-1)+e(n-2)]
(4)
1.2 模糊PID控制器
模糊集合理論(Fuzzy Sets)[5]是美國加州大學Zadeh L A教授于1965年提出來的,其實質就是在描述復雜系統時,當有效性和精確性無法兼顧時可以進行模糊處理。
設X是對象x集合,x是X上任意一個元素。X上的模糊集合A定義為一組有序對。
A={(x,μ(x))|x∈X}
(5)
其中μ(x)稱為模糊集合A的隸屬函數(Member Function,MF),X稱為論域。模糊集合完全由隸屬函數所表征。模糊PID控制最重要的步驟是找出比例(Proportion)、積分(Integration)和微分(Differentiation)系數與誤差e、誤差對時間的一階導數ec之間的關系,關系的建立主要基于以下幾個原則[8]:
(1)當|e|較大時,為使系統具有較好的跟蹤性能,Kp應取較大,Kd應取較小。同時為了避免出現較大的超調,應對積分作用加以限制,Ki通常取0;
(2)當|e|處于中等大小時,我們希望系統響應具有較小的超調,Kp應取得盡量小,此時,Kd的大小對系統響應的影響就比較大,Ki的取值要適當。
(3)當|e|較小時,為使系統具有較好的穩定性能,Kp和Ki的值都應取的大些,同時為避免系統出現振蕩,Kd值的選擇根據ec來確定;當ec值較小時Kd取大些,當ec值較大時Kd取小些,Kd值通常是中等大小。
然后根據規則列出模糊規則表,實現在線自適應調整。
1.3 高精度模糊PID控制器
高精度模糊控制器采用變論域(Variable Universe)思想,思想的實質是根據實時變化的實際情況對原先不能改變的初始論域進行在線自適應的論域伸縮。
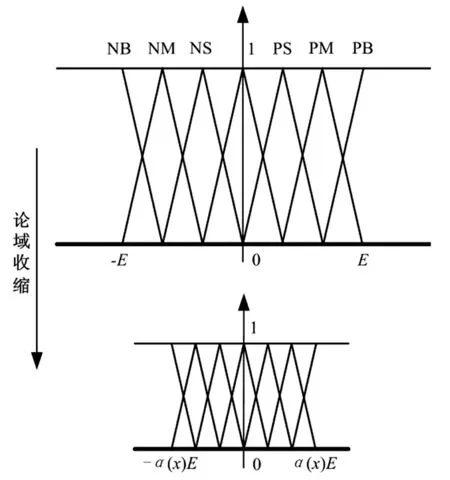
圖1 論域壓縮
常用的模糊控制規則模型如Mamdani模型等,從數值分析的角度理解,皆為一種插值函數。兩峰點之間的距離就決定了精度的高低。傳統的模糊控制不能改變峰點之間的間距,精度基本不變,不能使模糊規則更好地發揮控制作用。因此,我們引進伸縮因子α(x)和β(x)[1-2],不妨假設輸入變量的初始論域Xi=[-Ei,Ei](i=1,2,…),添加伸縮因子之后變成Xi=[-α(x)Ei,α(x)Ei],其中α(x)是輸入變量x的連續函數,且滿足:
α(x)=1-λe-kx2λ∈(0,1)k>0
(6)
同理β(x)作用于輸出變量論域中,且滿足要求:
(7)
變論域的關鍵就在于確定伸縮因子的大小,使得最終的控制效果達到最優。
2 水輪機調節器數學模型
水輪機調節器的數學模型我們都以傳遞函數的形式來表示,對于線性定常系統的的傳遞函數,是分別通過Laplace變化的輸出量與輸入量的比值,以s為變量的代數方程。
電液隨動系統的數學模型為:
(8)
式中Ty是主接力器時間常數;Ty1是引導閥和輔助接力器時間常數。當Ty1與Ty相比小得多時,上式近似表示為:
(9)
水輪機組段數學模型(以y→mt為例):
(10)
式中ey是水輪機力矩對導葉開度的傳遞系數;eqy是水輪機流量對導葉開度的傳遞系數;eqh是水輪機流量對水頭的傳遞系數;Gh(s)是有壓過水系統傳遞函數,假設為剛性水擊,即認為管壁和水流都不可壓縮,Gh(s)= -Tωs,Tω是水流慣性時間常數。
上式可簡化為:
(11)
水輪機力矩到發電機轉速的數學模型:
(12)
式中Ta是機組慣性時間常數;eg發電機(負荷)自調節系數;ex水輪機自調節系數。
3 高精度模糊控制器仿真
該水輪機調節器模型圖由圖2所示:
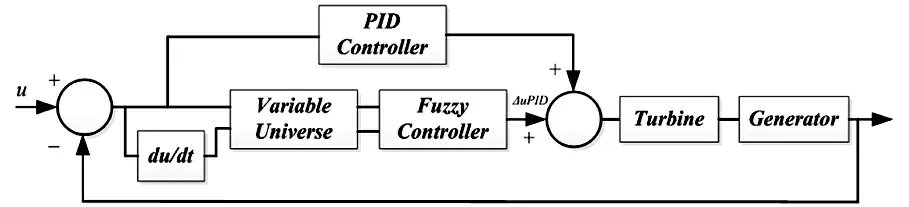
圖2 高精度模糊控制器模型
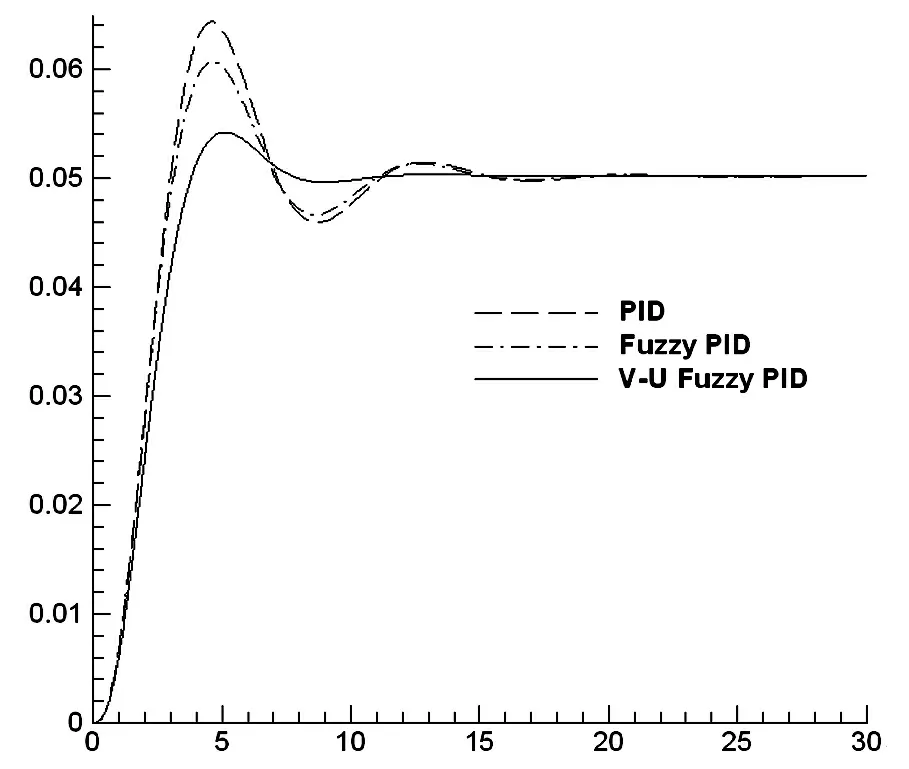
圖3 發電機頻率變化5%時階躍響應
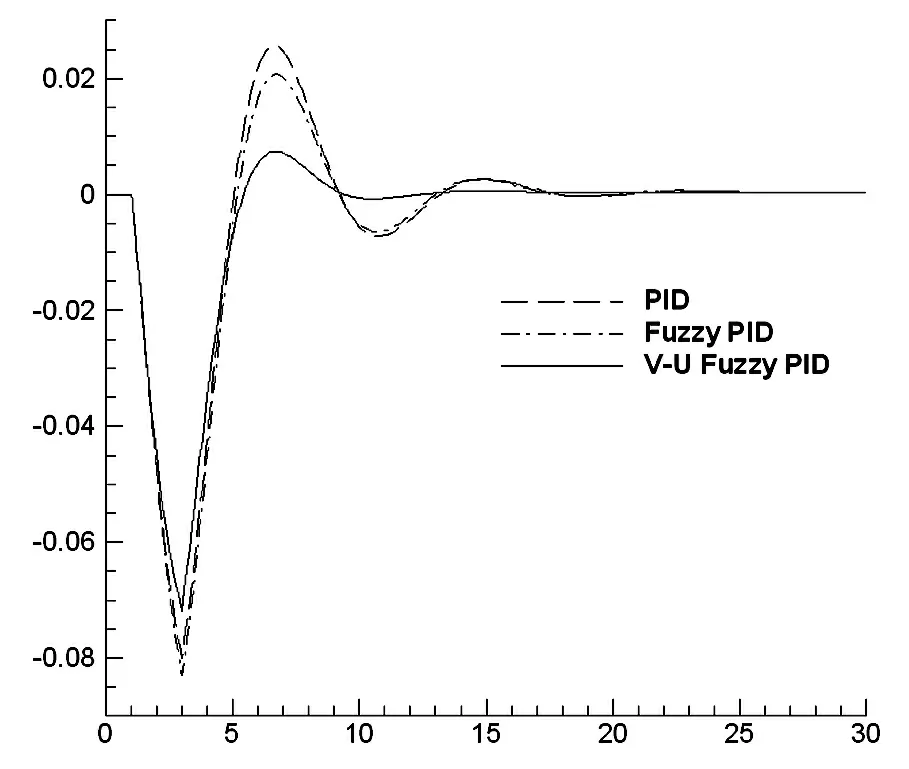
圖4 甩10%負荷時的發電機轉速階躍響應
其調節對象的各項參數為:ey= 0.57,eqy=0.69,eqh=0.51,Tω=1.45 s,Ta=5.66 s,eg-ex=1。以下我們分別對比傳統PID控制器、模糊PID
控制器和高精度模糊控制器分別在兩種工況下的狀態響應。
(1)無負載擾動的情況下,增加2.5Hz的頻率擾動。
(2)無頻率擾動的情況下,加入10%的負載擾動,見圖4。
4 結 論
通過傳統PID控制器、模糊PID控制器和高精度模糊PID控制器在頻率擾動和負荷擾動兩種工況下的擾動可以清晰的看到,高精度模糊控制器相比于另外兩種控制器,動態特性好,曲線過沖小,較強的抗擾動能力;調節能力強,速度快且過程平穩;魯棒性強,綜合性能較優。是一種行之有效的控制方法,該高精度模糊控制器在工業系統控制中將有廣闊的應用前景。
參考文獻:
[1] 李洪興. 變論域自適應模糊控制器[J].中國科學(E輯),1999,29(1):32-42.
[2] 李洪興.非線性系統的變論域穩定自適應模糊控制器[J].中國科學(E輯),2004,32(2):211-223.
[3] 陳國平,孫培德,李俐,等.模糊控制器在水輪機調節中的應用及Simulink仿真[J].水力發電,2006,32(7):53-55.
[4] 喻菁,周建中.模糊PID控制在水輪機調節中的應用研究[J].水利科技,2003,1:49-54.
[5] 李洪興. Fuzzy控制的本質與一類高精度Fuzzy控制器的設計[J].控制理論與應用,1997,14(6):868-872.
[6] 田勇,沈祖詒.水輪機調解中高精度模糊控制器的應用[J].水利水電科技進展,2006,26(5):55-58.
[7] Zadeh L A. Fuzzy Sets[J]. Information and Control,1965,8:338-353.
[8] 李勇. 水輪機調節系統模糊PID控制器設計及仿真研究[J].工程技術,2010,75-79.
作者簡介:
曹 歡(1984-),男,湖北鐘祥人,工程師,電氣工程及其自動化本科畢業,從事水電廠運行維護工作;楊 棣(1990-),男,山東無棣人,助理工程師,熱能與動力工程本科畢業,從事水電廠運行維護工作.

