基于EKF和自適應抗差濾波的星載GPS定軌方法

段 宇，吳江飛

(信息工程大學 地理空間信息學院，河南 鄭州 450052)

基于EKF和自適應抗差濾波的星載GPS定軌方法

段 宇，吳江飛

(信息工程大學 地理空間信息學院，河南 鄭州 450052)

針對在星載GPS衛星定軌中由于衛星動力學模型誤差和不可避免的觀測異常嚴重影響定軌精度的問題，通過采用適當的自適應控制因子和應用抗差估計原理，構造自適應抗差擴展卡爾曼濾波(RAEKF)來實現星載GPS衛星定軌。實測計算表明，自適應抗差擴展卡爾曼濾波對觀測誤差和狀態擾動有一定的抵制能力，與一般擴展卡爾曼濾波相比提高了精度，證明其理論的可行性。

非線性濾波；定軌；擴展卡爾曼濾波；自適應濾波；抗差估計

國內外學者提出多種自適應濾波算法并廣泛地應用于各種工程實踐中[1-3]。利用抗差估計原理也可以實現動態系統的自適應濾波[3]。卡爾曼濾波應用于星載GPS實時定軌的情況下，由于一方面低軌衛星的受力情況復雜，其動力學模型的精確度難以保證。另一方面其數據采集裝置星載GPS接收機處在外空高速運動狀態，環境變換大，可觀測性不強。這些特點導致星載GPS觀測值出現異常甚至粗差的幾率與地面觀測的情形相比有明顯的增大。上述問題若無法解決，卡爾曼濾波結果的精確性和穩定性會顯著降低，嚴重情況下甚至會導致濾波器的發散。因此，在使用卡爾曼濾波器進行迭代計算時，對于狀態噪聲協方差矩陣和觀測噪聲協方差陣采用抗差估計的原理自適應的求解，可以有效地減弱和控制觀測噪聲和狀態噪聲對狀態估計的影響[4-5]。

EKF(extended Kalman filter)是一種非線性濾波算法。它是在卡爾曼濾波的框架下，使用展開泰勒級數的方法對動態方程和誤差方程作一階線性化處理，來近似非線性濾波的方法[6]。它是到目前為止應用最為廣泛的一種非線性濾波，且在某些情況下仍為解決問題的最佳方法[7-8]。本文基于非線性濾波EKF研究了一種新的非線性自適應抗差濾波(adaptively robust extended Kalman filter， AREKF)，并將這種算法在MicroLab-1衛星的精密定軌中進行應用，實測計算結果證明該算法的有效性和可行性。

1 非線性自適應抗差濾波[9]

本文研究的衛星軌道確定問題是一個非線性系統。非線性系統的狀態方程和觀測方程分別為

Xk=f(Xk-1)+Wk,

(1)

Lk=h(Xk)+ek.

(2)

式中：Xk為狀態向量；f(·)為狀態轉移方程；Wk為狀態噪聲向量；Lk為觀測向量；h(·)為觀測方程；ek為觀測噪聲向量。其中Wk和ek的期望為零，且不相關，協方差分別為∑Wk和∑k。

為控制觀測異常和狀態噪聲導致的狀態預測信息異常對狀態參數估值的影響，可以構造如下極值原則：

n.

(3)

對式(3)求極值可得

).

(4)

在擴展卡爾曼濾波框架下，式(4)可等價為

).

(5)

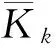
(6)

狀態向量驗后協方差矩陣為

(7)

由以上公式可得，要實現自適應抗差濾波，就必須求得觀測向量等價協方差矩陣和自適應因子。

1.1 觀測噪聲等價協方差陣[3]

觀測向量等價協方差陣可通過雙因子方差膨脹模型求得[9]。觀測向量的協方差矩陣是一種觀測量的精度評定指標，它能夠定量地反映觀測量的離散程度。如果觀測向量等價協方差小，則說明觀測量的質量好，精度高，該觀測所占的權重就大；相反地，若觀測量的質量較低，精度一般，則該觀測所占的權重就小。

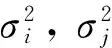
(8)

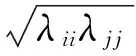
由此生成的協方差矩陣稱為等價協方差矩陣。由上述推導可以知道，通過加入膨脹因子構造的等價協方差陣仍然能夠與原來的協方差陣保持相關性。

為了在觀測誤差超過閾值時，相應的方差膨脹，否則原有的方差不變，以λii為例，其膨脹因子可構造為

(9)

(10)

式中:vi，σvi分別為殘差向量Vk和殘差向量協方差矩陣∑Vi中的元素。可由以下公式求得

(11)

(12)

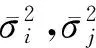
由膨脹因子的構造過程可以得知，當觀測值的誤差超過某一設定值時，相應的方差會膨脹，即對原協方差矩陣作降權處理。反之，膨脹因子的值為1，原方差保持不變。

1.2 自適應因子

不同的誤差判別統計量[10]或衡量了動態載體實時位置狀態與模型標定狀態的差異，或衡量了動力學模型的誤差大小。基于這樣的原理，可以構造自適應因子α，以調節狀態信息與觀測信息對參數估計的影響。本文中選擇了兩段函數模型作為自適應因子，其具體形式為

(13)

(14)

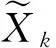
(15)

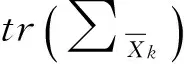
1.3 非線性自適應抗差擴展卡爾曼濾波算法

以標準EKF算法框架為基礎，結合1.1、1.2所述理論，可以建立如下的非線性自適應抗差卡爾曼濾波算法：

狀態更新：

(16)

(17)

量測更新：

(18)

(19)

(20)

2 計算與分析

為了驗證所提出的算法性能，實驗中選取MicroLab-1衛星星載GPS接收機所采集的數據進行定軌解算[11]。在數據處理時進行了一定的簡化。本算例使用了預測殘差統計量作為誤差判別統計量，采用兩段式函數構成自適應因子。對于膨脹因子和預測殘差統計量的閾值選取，經過多次計算和比較，確定為0.9和0.8。

本算例中為研究自適應抗差濾波的性能，設置了A，B，C 3種情況，其參數設置如表1所示；同時將24 h內分別由標準擴展Kalman濾波(EKF)和抗差自適應Kalman濾波(RAEKF)計算的位置誤差和速度誤差繪制成圖，如圖1～6所示。

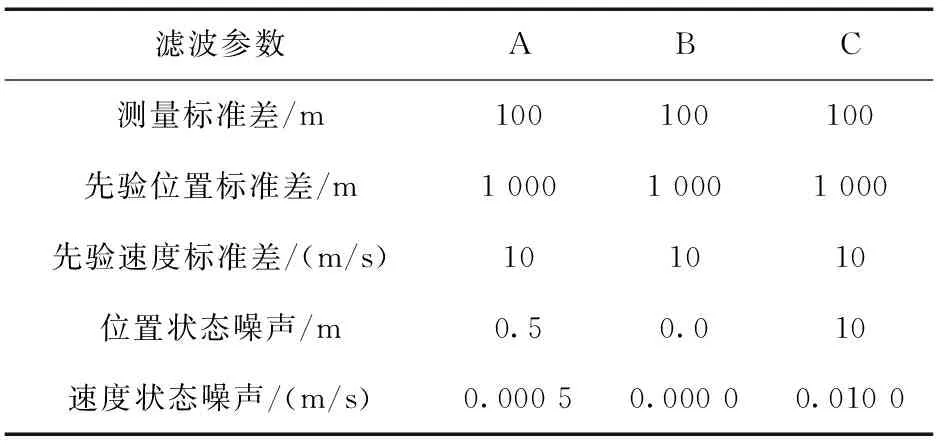
表1 A，B，C 3種情況下的濾波參數

圖1 情況A的位置誤差

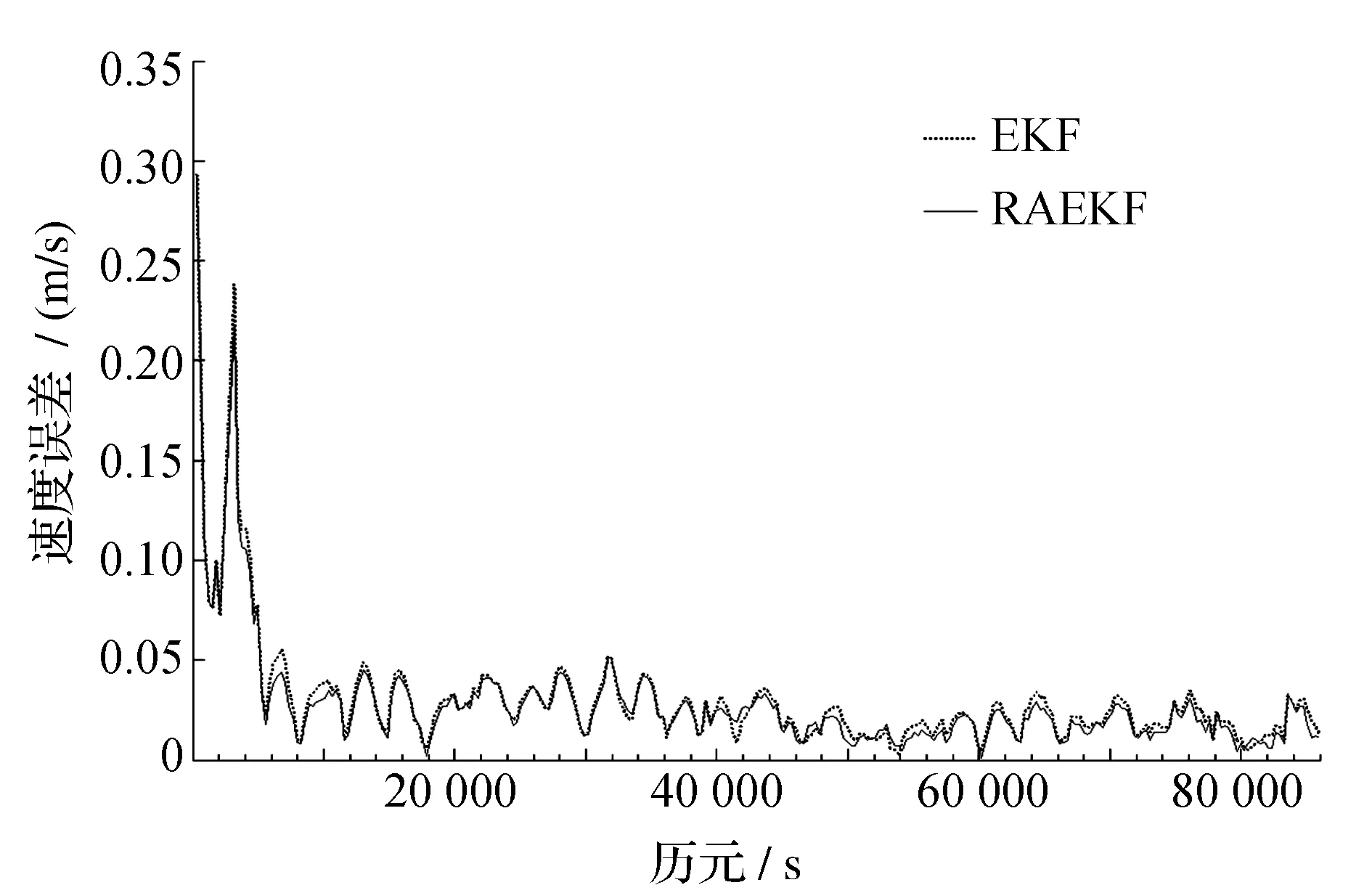
圖2 情況A的速度誤差

圖3 情況B的位置誤差

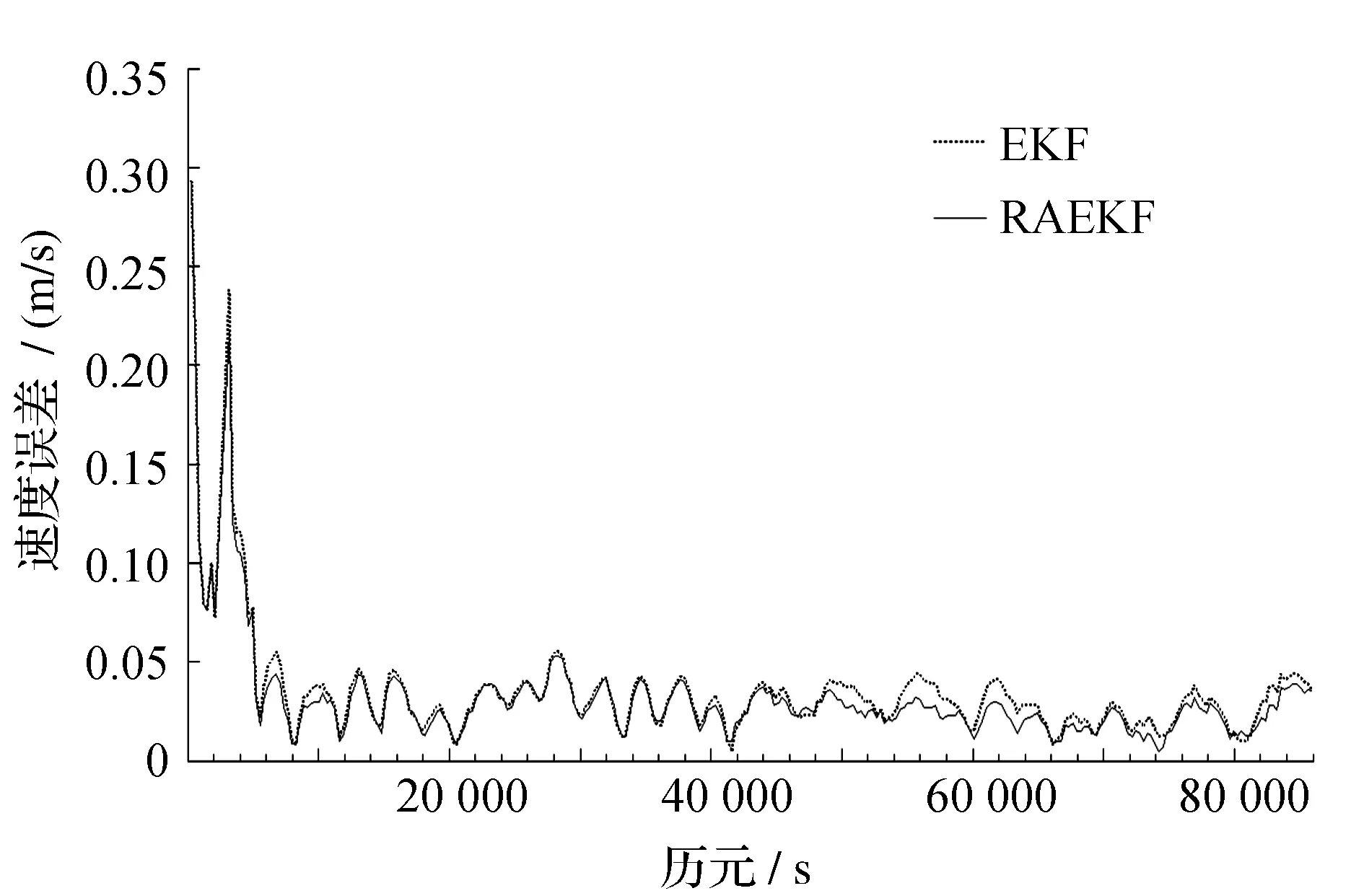
圖4 情況B的速度誤差

圖5 情況C的位置誤差

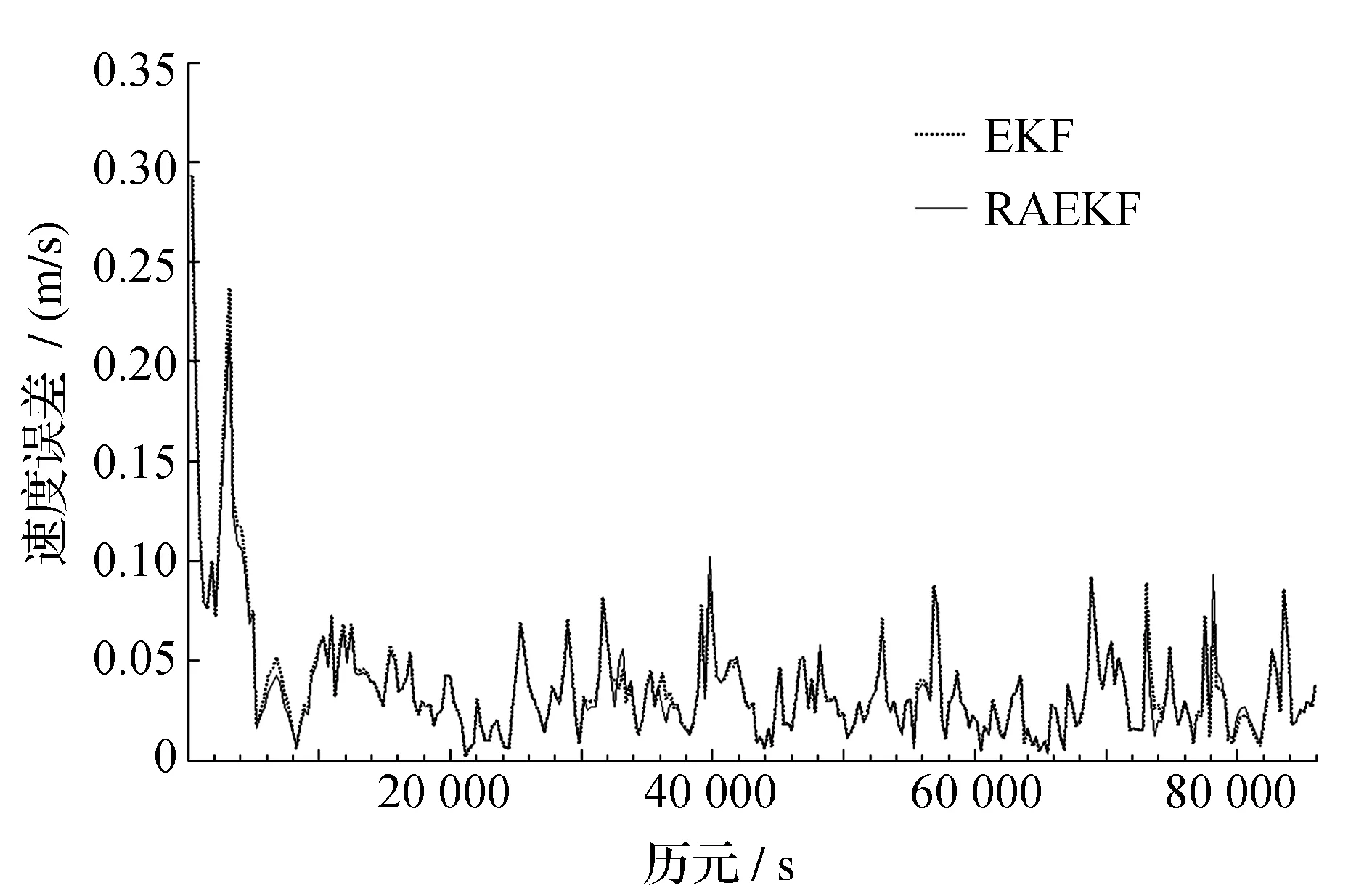
圖6 情況C的位置誤差

由圖1～6可以得出：

1)濾波結果在前5 000 s 歷元內極不穩定，位置誤差最大約達180 m，速度誤差最大達0.29 m/s，其后趨于穩定,這是由濾波的原理造成的；

2)自適應抗差濾波相對于EKF的濾波結果有所改善，大部分歷元的誤差均有所降低，但誤差仍在同一個數量級；

3)從自適應抗差濾波結果相對EKF濾波結果的改善情況來看，情況B改善最大，誤差減小幅度最大，情況A次之，情況C基本無明顯改善，說明狀態噪聲的權越大，自適應抗差濾波的效果越明顯。

均方根誤差(RMS)是估值與真值之差的平方與觀測次數比值的平方根，能很好地反應出估值的精度。本算例中，分別計算了狀態向量估值各維的均方根誤差和位置、速度均方根誤差。其中位置分量的均方根誤差[12]計算公式為

(21)

(22)

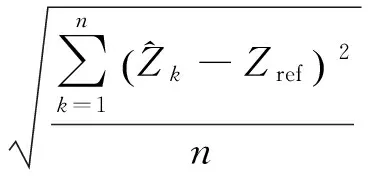
(23)

(24)

速度分量的均方根誤差計算公式依此類推。其計算結果如表2所示。

表2給出了A，B，C 3種方案的RMS誤差統計結果。可以看出，AREKF的軌道確定結果在各個分量上的RMS誤差均小于EKF的軌道確定結果在各個分量上的RMS誤差。各種情況的自適應抗差濾波結果的均方根誤差相對于EKF均有所減小，說明估值的精度均有所提高，但并不十分明顯，其中，情況B精度提高最大，情況A次之，情況C精度提高最小。這與上圖的分析是一致的。

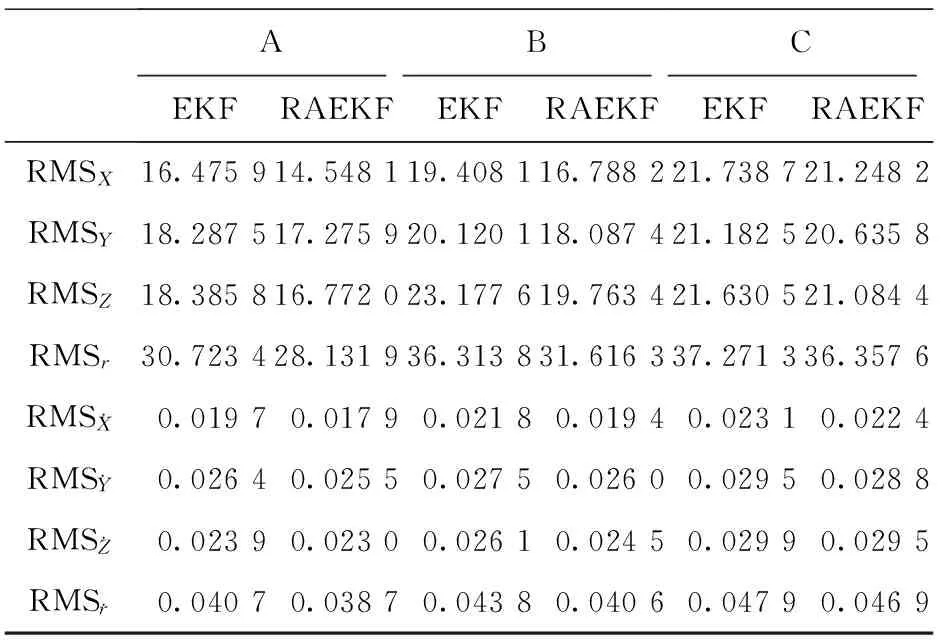
表2 A，B，C 3種方案的RMS誤差統計結果 m

3 結束語

結合上一節的圖表可知，個別歷元自適應抗差濾波的解反而比EKF解的誤差更大。這一方面是因為原始觀測數據誤差較大，無論使用何種濾波方法均不可能實現高精度的定軌，另一方面因為自適應抗差濾波只是修改了觀測噪聲協方差陣和預測狀態協方差陣，只能消減觀測誤差和狀態噪聲的擾動對濾波結果的影響，提升總體濾波精度，并不能使每個歷元的誤差都降低。總的來說，本文提出的自適應抗差擴展卡爾曼濾波算法(RAEKF)對狀態擾動和觀測誤差有一定的抵制能力，與標準擴展卡爾曼濾波(EKF)相比提高了精度，證明其理論的可行性。

[1]YANG YUANXI，HE HAIBO，XU GUOCHANG. Adaptively Robust Filtering for Kinematic Geodetic Position[J]. Journal of Geodesy，2001，75(2)：109-116.

[2]楊元喜，何海波，徐天河. 論動態自適應濾波[J]. 測繪學報，2001,30(4)：293-298.

[3]楊元喜，文援蘭. 衛星精密軌道綜合自適應抗差濾波技術[J]. 中國科學(D輯)，2003,33(11)：1 112-1 119.

[4]陳蕾，劉立龍，陳東銀. 自適應卡爾曼濾波法用于變形監測數據處理[J]. 測繪工程，2008,17(1)：48-54.

[5]李勇軍，左娟. GPS動態定位自適應卡爾曼濾波算法研究[J]. 測繪工程，2012,21(4)：30-32.

[6]吳江飛. 星載GPS衛星定軌若干問題的研究[D]. 上海：中國科學院上海天文臺，2006:100-101.

[7]郭雪姣. 非線性濾波算法研究及其在衛星高精度定軌中的應用[D]. 長沙：國防科技大學,2010:23-24.

[8]吳江飛，雷輝，王世忠. 一種新型非線性濾波理論及其應用[J]. 測繪工程，2008,17(6)：16-19.

[9]吳江飛，黃珹. 非線性自適應抗差濾波定軌算法研究[J]. 武漢大學學報：信息科學版，2008,33(2)：187-190.

[10]楊元喜. 自適應動態導航定位[M]. 北京：測繪出版社，2006.

[11]OLIVER MONTENBRUCK，EBERHARD GILL. Satellite Orbits[M]. Berlin：Springer-Verlag，Germany，2000：297.

[12]武漢大學測繪學院測量平差學科組. 誤差理論與測量平差基礎[M]. 武漢：武漢大學出版社，2003.

[責任編輯：劉文霞]

Methodofsatellite-borneGPSorbitdeterminationbasedonEKFandadaptiverobustfilter

DUAN Yu, WU Jiang-fei

(School of Geospatial Information, Information Engineer University, Zhengzhou 450052, China)

The satellite dynamic model errors and the inevitable observation anomaly have a serious influence on the orbit determination accuracy of satellites based on GPS. An appropriate adaptive control factor and the robust estimation theory are used to establish an adaptive robust extended Kalman filter(AREKF) to complete the orbit determination of satellites based on GPS. The measured calculation shows that the adaptive robust extended Kalman filter serves a certain resistance against the observation error and state disturbance. The precision is improved and the feasibility of the theory compared with the standard extended kalman filter is verified.

nonlinear filter; orbit determination; EKF; adaptive filter; robust estimation

2013-03-19

國家自然科學基金資助項目(41174006;40974010;41274016)

段 宇(1989-)，男，碩士研究生.

P228.4

：A

：1006-7949(2014)01-0021-04