培養學生自主探究的一種教學模式
肖 爽(江蘇省沛縣中學)
本文以高中數學蘇教必修一《指數函數》(第1課時)為例,就具體教學環節的處理和案例所體現出的教學理念作一些分析.
一、教學環節
1.問題引入
某種細胞分裂時,由1個分裂成2個,2個分裂成4個,……試寫出該細胞分裂的數學模型(設1個細胞分裂x次后,得到的細胞個數為y,在下表中x依次取值1、2、3……歸納出y與x的函數關系式,并觀察圖象).

(說明:本部分用Excel軟件制作,當學生輸入相應的x與y的值后,其右邊的圖象會隨數據動態產生)
以問題形式引入,重視學生的參與,強調從“形”入手增加學生對指數函數的感性認識.課件動態處理數據的功能使學生在自主操作過程中充分與計算機進行互動.
2.描點法畫圖象
結合以下問題探討:
(1)用描點法畫y=2x圖象時,請多嘗試幾組x的值,比較哪一組數據更能精確描述函數y=2x的圖象(可與同學進行對比).
(2) 由y=2x的圖象能畫出欄中的數據在正確位置上輸入論.

(說明:本部分用Excel軟件制作,輸入x的值后y=2x的值便自動給出,其相應圖象會隨數據動態產生,而值要自己輸入)
案例比較注重讓學生親身體驗畫圖象的過程,要求學生自己輸入x值,2x值與圖象都由計算機幫助處理,使學生有更多時間嘗試輸入幾組x值進行圖象對比,在強調了學生的個性差異的同時又能讓學生在對比中學會分析問題.對于函數案例中不直接提供數據,而是提示學生利用現有數據進行觀察,從而讓學生在“數形”兩方面深刻地理解了兩個函數的關系與對比,既強調了學生的主動參與和探究,又注重培養學生收集數據、處理數據的能力.
3.研究函數性質
結合問題自主操作,探討y=ax的性質:
(1) 當 a=1,a=0,a<0時情況如何,為什么?
(2) 對a>1時函數圖象與性質進行分析,
①定義域是多少?
②圖象的分布(值域) .
③圖象是否過一定點,為什么?
④函數的單調性.
(3) 當0 (4) 對比 y=ax和 y=a-x的圖象與性質. (5)當a>1時,要使圖象在y=1上方,x的取值范圍是多少? (6)探究性問題:當a變化時,函數圖象的變化規律是什么? (7)比較數21.5與21.6的大小,并探討此類題的解法. 案例把畫圖象和性質探討作為本節課的重點.本案例利用《幾何畫板》強大的交互功能,設計循序漸進的問題鏈,讓學生在動態的、開放的“數學實驗室”里自主探究.學生實時拖動動點B,改變y=ax中a的值,觀察連續變化的函數圖象并進行個性化的研究(相比較,案例A只是孤立地研究了a=2和的兩種靜止狀態).通過學習,學生對以下幾點應該有了深刻認識: ①y=ax中a的取值范圍; ②a>1時函數的定義域、值域、單調性等; ③學會對a>1與0 ④利用圖象解不等式ax>1; ⑤利用單調性比較大小; ⑥對過定點的探究; ⑦當a>1時,a變化時函數圖象的變化趨勢. 其中①②③屬基礎知識范疇;④⑤屬圖象與性質的應用范疇;⑥⑦屬進一步探究范疇.可以說,通過“做數學”,學生不但對指數函數從“數”和“形”兩方面都有了較深刻的理解,而且會逐漸體會到變化情形中有不變性與變化性,并由操作感知進一步升華為變化統一的數學思想. 例 1:已知指數函數 f(x)=ax(aφ0,且 a≠1) 的圖象經過點 (3,π),求 f(1),f(-3) 的值. 例2:利用指數函數的性質,比較下列各題中兩個值的大小: (1) 1.7a與 1.7a+1(2) 0.8-0.1與 0.8-0.2 設計較簡單的練習,能使學生對指數函數圖象性質進行簡單應用、鞏固整理. 本案例屬網絡探究課,強調學生自主探究,在學習過程中,教師不直接將教學內容講授給學生,而是設計一些具有誘導性的問題,使學生利用問題鏈,通過自主操作參與知識和規律的發現與驗證,引導自己不斷操作嘗試,在不斷錯誤和修正錯誤的過程中進行一步步深入探索. 學生的學習是主動的,具有探究性,又具有合作性.學生始終圍繞問題鏈進行自主探究,若在數據的收集處理與對動態圖象的操作中發現問題,學生或多次嘗試,或請教老師,或與同學討論以解決問題. 本案例側重基礎知識的掌握,更注重培養學生的自主探究能力.整個教學過程從提出問題開始到解決問題結束,引導學生在學習中做到“學中有探”、“探中有學”.在解決問題的過程中,通過發現新問題、解決新問題,培養學生的探究意識、創新精神和實踐能力,使學生學會自主學習、探究學習和合作學習. 案例導學教學方法使學生學習的目標更加明確,重點更加突出,問題設計更加具有針對性,有效調動了廣大學生學習的積極性.教師主觀能動性的充分發揮和設計巧妙的學案,使“學例導學”教學法在新課程的教學中再放光彩.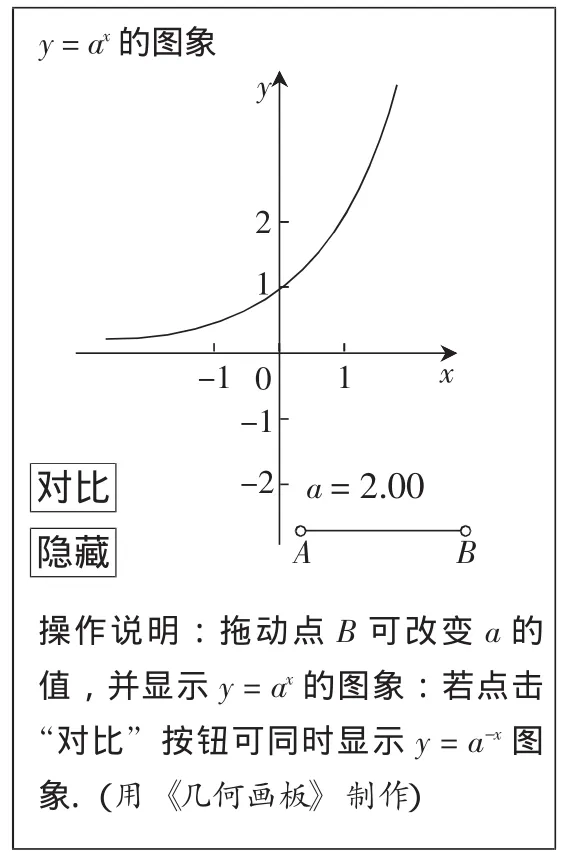
4.練習鞏固
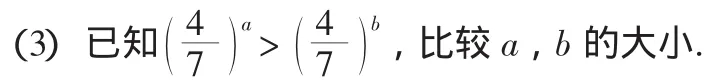
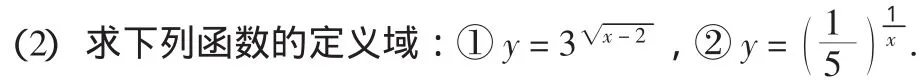
二、教學理念
1.課堂教學模式
2.學生學習方式
3.學生能力方面

