氣動干擾對串列雙幅類流線形斷面顫振的影響
劉小兵, 楊 群, 劉志文
(1. 石家莊鐵道大學 風工程研究中心, 石家莊 050043; 2. 石家莊鐵道大學 土木工程學院, 石家莊 050043;3. 湖南大學 風工程試驗研究中心, 長沙 410082)
氣動干擾對串列雙幅類流線形斷面顫振的影響
劉小兵1,3, 楊 群2, 劉志文3
(1. 石家莊鐵道大學 風工程研究中心, 石家莊 050043; 2. 石家莊鐵道大學 土木工程學院, 石家莊 050043;3. 湖南大學 風工程試驗研究中心, 長沙 410082)
針對串列雙幅類流線形斷面,在均勻流場中進行了一系列的顫振穩定性風洞試驗,并將試驗結果與單幅類流線形斷面的試驗結果進行了對比。研究結果顯示:氣動干擾降低了雙幅類流線形斷面的顫振臨界風速,間距越小,降低幅度越大;氣動干擾增大了雙幅類流線形斷面的顫振頻率,間距越小,增大幅度越大;與單幅類流線形斷面相比,氣動干擾使雙幅類流線形斷面的軟顫振特性更明顯。
氣動干擾;串列雙幅類流線形斷面;顫振;風洞試驗
近年來,隨著社會經濟的蓬勃發展,交通量日益增長。為了提高橋梁通行能力,通常將主梁設計成彼此分離且相互平行的雙幅橋面。工程實踐中,雙幅橋面橋梁通常有兩種形式:(1)橋梁新建時將主梁設計成分離平行的雙幅橋面,兩橋面同時建造并同時投入使用,如美國德克薩斯州1995年建成的跨越休斯頓航道的Fred Hartman橋、我國2006年建成的佛山平勝橋以及在建的青島海灣大橋紅島航道橋等等;(2)在已建橋梁一側再修建一座與其平行的橋梁,如美國分別于1950年和2007年建成的塔科馬橋、日本分別于1985年和1996年建成的名港西橋以及韓國分別于1984年和2005年建成的珍島橋等等。這兩類橋梁主梁間距都不大,上游橋面與下游橋面在來流風作用下相互干擾,雙幅橋面的風荷載、渦振特性及顫振穩定性等與單幅橋面相比存在一定的差異[1-2]。系統研究氣動干擾對雙幅橋面靜力系數、渦激振動及顫振的影響規律對于雙幅橋面橋梁的抗風設計具有重要意義。由于過去雙幅橋面橋梁建設不多,所以目前相關的氣動干擾研究文獻相對較少,且主要是針對特定的橋梁工程展開的[3-10]。
本文以大跨度橋梁中經常應用的類流線形斷面為對象,通過風洞試驗研究了氣動干擾對串列雙幅類流線形斷面顫振臨界風速和顫振頻率的影響,并從顫振導數出發分析了氣動干擾機理。
1 風洞試驗簡介
風洞試驗在湖南大學HD-2風洞高速試驗段進行。采用彈性懸掛二元剛體節段模型的方式進行風洞試驗。類流線形斷面的幾何參數見圖1,單幅斷面寬B=40.392 cm(不含風嘴的斷面寬度b=30 cm),高H=6 cm,寬高比B/H=6.732(不包含風嘴的斷面寬度與斷面高度之比b/H=5)。兩幅斷面之間的凈間距為D。
為了方便改變試驗參數,設計了針對雙幅斷面顫振氣動干擾的試驗裝置,如圖2所示。單幅節段模型由8根彈簧懸掛。在試驗段上頂板和下底板分別固定兩片槽鋼。節段模型上方的4根彈簧通過帶鉤的活動螺栓和上頂板槽鋼內的可滑動鋼塊連接。節段模型下方的4根彈簧通過帶鉤的活動螺栓與力傳感器連接,力傳感器再與下底板槽鋼內的可滑動鋼塊連接。通過滑動槽鋼內的鋼塊可以整體平移節段模型,實現上下游模型間距的改變。通過力傳感器測量上下游斷面模型的振動位移時程。為了有效防止模型在高風速下發生順風向側移,在模型來流前方大約10 m的位置固定兩根立柱,通過細鋼絲把立柱與模型兩邊的鐵軸相連。
試驗在均勻流場中進行,空風洞順風向紊流度約為1%。首先進行單幅模型試驗,然后進行不同間距串列雙幅模型試驗。對于雙幅模型,選擇了D/B=0.3、0.6、1.0、2.0、4.0和5.0六個間距進行研究。表1列出了試驗參數。上下游模型的頻率保持一致,阻尼大體接近。

圖1 雙幅類流線形斷面的尺寸(單位:cm)Fig.1 Dimension of twin streamline-liked sections (unit: cm)

圖2 風洞試驗照片Fig.2 Photo of wind tunnel test
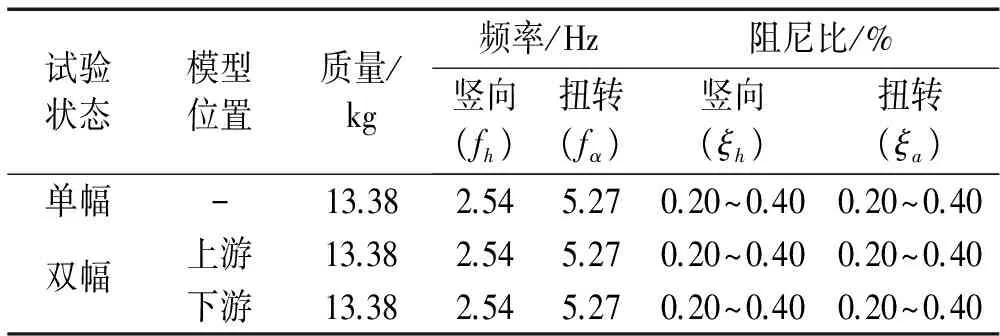
試驗狀態模型位置質量/kg頻率/Hz阻尼比/%豎向(fh)扭轉(fα)豎向(ξh)扭轉(ξa)單幅-13.382.545.270.20~0.400.20~0.40雙幅上游13.382.545.270.20~0.400.20~0.40下游13.382.545.270.20~0.400.20~0.40
2 氣動干擾試驗結果
圖3為不同無量綱風速下單幅類流線形斷面扭轉角位移時程曲線及幅值譜。圖4為D/B=0.6時不同無量綱風速下雙幅類流線形斷面扭轉角位移時程曲線及幅值譜。圖5為單幅類流線形斷面與不同間距雙幅類流線形斷面扭轉角位移根方差隨無量綱風速變化曲線。圖中無量綱風速Vr的定義如下:
(1)
其中,U為來流風速,ft為模型的扭轉頻率,B為模型寬度。
從圖3~圖5可以看到:(1)單幅斷面接近無量綱顫振臨界風速10.67時,扭轉角位移急劇增大,表現出較明顯的硬顫振形態。與單幅斷面相比,雙幅斷面的軟顫振表現得更明顯。上下游兩斷面的扭轉角位移根方差隨無量綱風速的增大逐漸增大,變化曲線在顫振臨界風速附近的斜率轉折不如單幅斷面明顯。(2)同一無量綱風速,下游斷面扭轉角位移根方差大于上游斷面扭轉角位移根方差。這表明,與上游斷面相比,下游斷面的穩定性更差。(3)顫振過程中,上下游兩斷面振動并不同步,二者存在相位差。(4)上下游兩斷面的顫振頻率保持一致,且介于固有豎向頻率和固有扭轉頻率之間。
表2列出了按0.5°扭轉角位移根方差標準得到的單、雙幅類流線形斷面的無量綱顫振臨界風速及顫振頻率。需要說明的是,表中雙幅斷面的顫振臨界風速及顫振頻率定義為干擾狀態下穩定性相對較差的一幅斷面對應的顫振臨界風速及顫振頻率。這一定義方式把兩分離斷面當作一個系統來考慮,而沒有單獨定義上、下游斷面的顫振臨界風速及顫振頻率。筆者認為這符合雙幅橋面橋梁顫振時的真實情況。

圖3 單幅類流線形斷面扭轉角位移時程曲線及幅值譜Fig.3Curvesoftorsionalangulardisplacementversustimehistoryandamplitudespectrumofsinglestreamline?likedsection圖4 雙幅類流線形斷面扭轉角位移時程曲線及幅值譜(D/B=0.6)Fig.4Curvesoftorsionalangulardisplacementversustimehistoryandamplitudespectrumoftwinstreamline?likedsections(D/B=0.6)

圖5 雙幅類流線形斷面扭轉角位移根方差隨無量綱風速變化曲線Fig.5 Curves of mean square root of torsional angular displacement versus dimensionless wind speed of twin streamline-liked sections

試驗狀態單幅類流線形斷面雙幅類流線形斷面D/B=0.3D/B=0.6D/B=1D/B=2D/B=4D/B=5無量綱顫振臨界風速10.674.876.267.469.5610.0010.20顫振頻率3.995.054.864.634.244.174.11
圖6和圖7分別顯示了不同間距雙幅類流線形斷面的無量綱顫振臨界風速干擾因子IFv和顫振頻率干擾因子IFf隨D/B的變化曲線。本文定義顫振臨界風速干擾因子和顫振頻率干擾因子如下:
(2)
(3)
從圖6可以看到:雙幅斷面的無量綱顫振臨界風速在D/B=0.3時僅為單幅斷面結果的45%;隨著間距的增大,逐漸與單幅斷面結果靠近;在D/B=5時約為單幅斷面結果的95%。這表明:氣動干擾降低了雙幅類流線形斷面整體的顫振臨界風速,間距越小,降低幅度越大。
從圖7中可以看到:雙幅斷面的顫振頻率在D/B=0.3時為單幅斷面結果的1.27倍;隨著間距的增大,逐漸與單幅斷面結果靠近;在D/B=5時約為單幅斷面結果的1.03倍。這表明:氣動干擾增大了雙幅斷面的顫振頻率,間距越小,增大幅度越大,顫振頻率越接近固有扭轉頻率。這也說明:雙幅類流線形斷面雖然仍發生彎扭耦合顫振,但隨著間距的不斷減小,彎扭耦合顫振形態逐漸向單自由度扭轉顫振形態轉移。
3 氣動干擾機理分析
顫振導數是橋梁斷面狀態向量到自激力的傳遞函數。氣動干擾對雙幅橋面顫振的影響源于對上下游兩橋面顫振導數的影響。鑒于此,本節基于顫振導數來分析串列雙幅類流線形斷面顫振的氣動干擾機理。從前節試驗結果可以看到,由于下游類流線形斷面的顫振穩定性比上游類流線形斷面差,雙幅類流線形斷面整體的顫振臨界風速往往取決于下游類流線形斷面的顫振臨界風速,因此,本文著重通過對比單幅類流線形斷面和雙幅下游類流線形斷面的顫振導數來分析氣動干擾機理。


圖6 雙幅類流線形斷面無量綱顫振臨界風速干擾因子隨D/B變化曲線Fig.6CurveofdimensionlessfluttercriticalwindspeedinterferencefactorversusD/Boftwinstreamline?likedsections圖7 雙幅類流線形斷面顫振頻率干擾因子隨D/B變化曲線Fig.7CurveofflutterfrequencyandinterferencefactorversusD/Boftwinstreamline?likedsections圖8 單幅類流線形斷面與雙幅下游類流線形斷面的顫振導數(□單幅△D/B=1☆D/B=4)Fig.8Flutterderivativesofsingleandleewardstreamline?likedsection(□single△D/B=1☆D/B=4)
基于CFD軟件Fluent計算了單幅類流線形斷面和雙幅下游類流線形斷面的顫振導數。單幅斷面顫振導數的獲取過程如下:首先數值模擬斷面分別做單自由度豎向強迫振動和單自由度扭轉強迫振動,然后分別提取兩種強迫振動下斷面的升力和扭矩,最后基于升力和扭矩按最小二乘法確定顫振導數。識別雙幅下游斷面的顫振導數時,保持上游斷面靜止不動并強迫下游斷面分別做豎向振動和扭轉振動。通過提取下游斷面的升力和扭矩來進行顫振導數識別。
4 結 論
本文通過風洞試驗研究了氣動干擾對均勻流場串列雙幅類流線形斷面顫振的影響,揭示了串列雙幅類流線形斷面的顫振氣動干擾規律,分析了串列雙幅類流線形斷面的顫振氣動干擾機理,得到了如下幾點結論:
(1) 氣動干擾降低了串列雙幅類流線形斷面的顫振臨界風速,間距越小,降低幅度越大。
(2) 氣動干擾增大了串列雙幅類流線形斷面的顫振頻率,間距越小,增大幅度越大。
(3) 與單幅類流線形斷面相比,串列雙幅類流線形斷面的軟顫振特性更明顯。
[ 1 ] Irwin P A, Stoyanoff S, Xie J M, et al. Tacoma Narrows 50 years later-wind engineering investigations for parallel bridges[J]. Bridge Structures: Assessment, Design and Construction, 2005, 1(1): 3-17.
[ 2 ] Larose G L, D’Auteuil A,Stoyanoff S. Aeroelastic model study for the twinning of the Tacoma Narrows Bridge[C]// The 4th International Conference on Advances in Wind and Structures. Jeju, Korea, 2008, 29-31.
[ 3 ] Kimura K, Shima K, Sano K, et al. Effects of seperation distance on wind-induced response of parallel box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6-7): 954-962.
[ 4 ] Sarkar P P, Jones N P, Scanlan R H. Identification of aeroelastic parameters of flexible bridges[J]. Journal of Engineering Mechanics, 1994, 120(8): 1718-1742.
[ 5 ] Sockel H, Watzinger J. Vibrations of two circular cylinders due to wind-excited interference effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 1029-1036.
[ 6 ] Honda A, Shiraishi N, Motoyama S. Aerodynamic stability of kansai international airport access bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33(1-2): 369-376.
[ 7 ] 陳政清, 劉小兵, 劉志文. 雙幅橋面橋梁三分力系數的氣動干擾效應研究[J]. 工程力學, 2008, 25(7): 87-93. CHEN Zheng-qing, LIU Xiao-bing, LIU Zhi-wen. Study of aerodynamic interference effects on aerodynamic coefficients of twin-deck bridges[J]. Engineering Mechanics, 2008, 25(7): 87-93.
[ 8 ] 朱樂東, 周奇, 郭震山,等. 箱形雙幅橋氣動干擾效應對顫振和渦振的影響[J]. 同濟大學學報(自然科學版), 2010, 38(5): 632-638. ZHU Le-dong, ZHOU Qi, GUO Zhen-shan, et al. Aerodynamic interference effects on flutter and vortex-excited resonance of bridges with twin-separated parallel box decks[J]. Journal of Tongji University(Natural Science), 2010, 38(5): 632-638.
[ 9 ] 郭震山, 孟曉亮, 周奇,等. 既有橋梁對鄰近新建橋梁三分力系數的氣動干擾效應[J]. 工程力學, 2010, 27(9): 181-186,200. GUO Zhen-shan, MENG Xiao-liang ZHOU Qi,et al. Aerodynamic interferences of an existed bridge on aerodynamic coefficients of an adjacent new bridge[J]. Engineering Mechanics, 2010, 27(9): 181-186,200.
[10] 劉小兵, 陳政清, 劉志文, 等. 均勻風場中串列雙矩形斷面氣動力干擾的數值研究[J]. 振動與沖擊, 2008, 27(12): 83-87. LIU Xiao-bing, CHEN Zheng-qing, LIU Zhi-wen, et al. Numerical study on interference of aerodynamic force on two rectangular sections with tandem arrangement in uniform wind field[J].Journal of Vibration and Shock, 2008, 27(12): 83-87.
Effects of aerodynamic interference on flutter of twin streamline-liked sections in tandem
LIU Xiao-bing1,3,YANG Qun2,LIU Zhi-wen3
(1. Wind Engineering Research Center, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;3. Wind Engineering Research Center,Hunan University, Changsha 410082, China)
A series of wind tunnel tests were performed to investigate flutter stability of twin streamline-liked sections in tandem. The test results were compared with those of a single streamline-liked section. The study results showed that the flutter critical wind speed of twin streamline-liked sections in tandem is decreased by aerodynamic interference, the smaller the distance between sections, the lower the flutter critical wind speed; the flutter frequency of two streamline-liked sections in tandem is increased by aerodynamic interference, the smaller the distance between sections, the higher the flutter frequency; the soft flutter characteristic of two streamline-liked sections in tandem is more obvious due to aerodynamic interference compared with that of a single streamline-liked section.
aerodynamic interference; twin streamline-liked sections in tandem; flutter stability; wind tunnel test
國家自然科學基金項目(50608030)
2013-02-19 修改稿收到日期:2013-05-30
劉小兵 男,博士,講師,1982年3月生
TU311.3
A
10.13465/j.cnki.jvs.2014.08.028

