基于PRO/E模型的潛器穩性計算

史戰新

(武漢第二船舶設計研究所, 湖北 武漢 430064)

基于PRO/E模型的潛器穩性計算

史戰新

(武漢第二船舶設計研究所, 湖北 武漢 430064)

潛器穩性校核的基礎是準確確定潛器的吃水線及浮心、重心位置。本文基于船舶穩性計算理論，結合潛器PRO/E三維模型，探索一種利用行為建模技術計算潛器穩性的方法。與傳統計算方法相比，行為建模自動迭代計算方法的效率與準確性均有所提高，也為船舶其他CAD三維軟件穩性計算提供參考。

潛器 PRO/E行為建模 穩性

1 概述

潛器在外力作用下偏離其平衡位置，而當外力消除后，船舶自身具有恢復到原來平衡位置的能力稱為穩性。船舶是否具有足夠的穩性是船舶是否適航的重要條件，潛器穩性校核是潛器航行及作業的重要安全保證。與水面船舶相比，潛器排水外形不規則，很多系統設備零散布置于耐壓殼體外，導致水線面隨吃水變化大，水線面輪廓不規則，形心難以采用傳統水面船舶的型值表方法計算，采用積分計算大量零散處置系統設備產生的浮力費時費力。本文提出利用PRO/E軟件對潛器排水部件進行簡化三維建模，基于船舶靜穩性曲線等排水量計算理論，利用PRO/E的行為建模功能實現潛器任意載重情況下吃水線確定和穩性的快速計算。

2 潛器穩性計算原理

由于潛器的不規則排水外形，致使水線面形狀不連續，且不同吃水下水線面形心及慣性矩變化大，潛器在水中橫傾或縱傾的等體積傾斜軸線不再通過正浮水線面的漂心，浮心的移動曲線不再是圓弧，其橫搖或縱搖的穩心隨傾角而變動，類似水面船舶的大傾角穩性計算工況。因此潛器的穩性嚴格來講只能采用船舶大傾角穩性計算原理取得，即求出在不同傾斜水線面下的靜穩性臂(浮心與重心橫向距離)，相關規范如DNV船級社也規定了靜穩性臂的數值范圍。

船舶靜穩性曲線計算有變排水量計算法和等排水量計算法兩種[1]。其中變排水量計算法是求得不同排水體積、不同橫傾角時浮力作用線至重心的距離，從而得到不同排水量下的靜穩性曲線。等排水量計算法的基本原理是：首先確定各傾角的等體積傾斜水線，然后分別計算這些水線下的浮心位置，從而獲得重心與浮心的距離即復原力臂。

3 傳統水面船舶計算步驟及缺點

傳統船舶穩性計算基于船舶小傾角和大傾角理論假設分為小傾角穩性和大傾角穩性。

對于小傾角穩性是利用船舶的型值表確定吃水線，然后根據水線面慣性矩、排水體積、浮心高、重心高計算初穩性。

對于大傾角穩性變排水量法是利用型值表畫出船舶乞氏橫剖面，計算一系列不同水線面的浮心位置和排水體積，從而得到穩性橫截曲線和靜穩性曲線，最后根據給定的排水量和重心高度篩選計算符合的靜穩性曲線。等排水量法根據給定的排水量計算吃水線，再利用公式得到靜穩性曲線。

然而傳統方法都無法避免根據型值表計算浮心、浮力的誤差，以及如何準確找到吃水線，使得浮心與重心橫向與縱向坐標重合，浮力與船舶質量一致。這是一個反復迭代計算的過程，手工計算費時費力，誤差也不可避免[2]。對于水面船舶來說，由于船殼外板規則且占排水體積比重大，附體少，達到0.1%誤差要求容易實現；然而對于潛器來講，附體較多，排水形狀極其不規則，傳統水線面計算將費時更多，誤差很難控制。

目前，各船舶穩性專業計算軟件如freeship、ESTAB、CCS船舶靜力學穩性計算軟件等主要針對水面船舶，具有一定局限性，且計算軟件針對性太強，只適用某幾種船型，與現行船舶規范銜接不合理，計算軟件穩性核算時需要錄入的數據，規范上沒有強制要求，如質量重心、艏艉端點、剖面底線數等[3]需要復核人員量取和估算，難免造成偏差和誤差。

4 PRO/E行為建模簡介

PRO/Engineer是美國PTC公司開發的參數化設計和基于特征設計的實體造型三維集成化軟件，廣泛應用于機械、航天、船舶領域。在常用的實體造型方法中，由于邊界表達法采用了自由曲面造型技術, 可以構造具有復雜曲面外型的浮體模型, 因而通過拉伸、旋轉、掃掠等實體的基本構造方法以及實體模型的布爾運算, 可以方便地建立各種復雜的潛器模型。

行為建模技術使工程師面對不斷變化的要求，進行高度智能優化設計主要表現在[4]：

(1) 按照產品的各種工程規范捕捉設計信息和過程信息，將規范定義為特征；

(2) 采取目標驅動方式，優化產品的尺寸參數，并可捕捉多個目標和需求變化，解決相互沖突的目標問題；

(3) 具有開放性可擴展環境，提供與其他軟件的無縫鏈接設計功能。

Behavioral Modeling功能是PRO/Engineer的一個功能擴展模塊，作為參數化設計中的分析工具，其主要作用是設置參數變量范圍，建立分析特征，通過改變參數來改變模型的結構外形，從而使設計過程更加智能化，更有效率，主要功能如下[5]：

(1) 獲得基于模型測量和分析的特征參數；

(2) 建立基于模型測量和分析的幾何實體；

(3) 創建新的測量類型,滿足特定應用要求；

(4) 進行靈敏度分析,估計設計參數改變后,對產品設計的影響；

(5) 對模型進行可行性分析和優化,獲得最佳設計參數,滿足產品要求。

其中敏感性分析適合于分析單個尺寸變量變化范圍內的多個目標值的變化,可輸出變量和目標值之間的關聯變化圖表。

可行性優化分析適合于多個變量和約束條件下尋找目標解決方案或最優目標值，其中梯度投影GDP搜索算法適合于在接近目標的同時產生一系列滿足限制的中間設計，使用當前模型條件作為起始點。MDS算法使用多目標設計研究算法來確定優化的最佳起始點，可在“最大迭代次數”(Max Ite-rations) 字段中指定要計算的起始點個數。此種方式更容易在設計參數和尺寸范圍內找到整體最優設計，但速度慢于GDP算法。

多目標設計是研究能夠幫助查找滿足多個設計標準(設計目標)的優化解決方案，采用樣本清單的方式列出所有可能方案，然后根據目標要求過濾、篩選出需要的可行性方案。

因此應用PRO/E行為建模技術,設置約束條件，進行水面線迭代計算，能快速、準確地找到吃水線，從而快速求解潛器靜穩性臂。

5 PRO/E軟件穩性計算步驟

5.1 模型簡化及假定重心

(1) 根據作業工況，確定潛器的排水零部件，將耐壓體殼體變為實體特征，建立排水零部件三維模型，設置組件密度為水密度，如圖1所示。

(2) 根據已知的重心位置，建立潛器相對坐標系，在模型中建立重心的點特征。

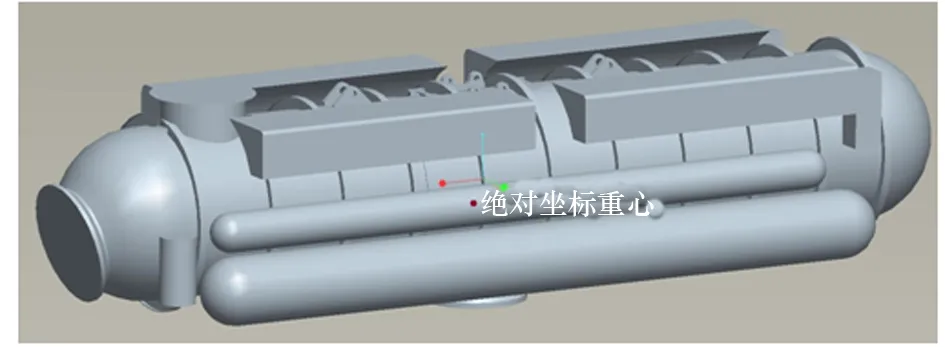
圖1 原始模型及假定重心

5.2 動態水線面假定

為了建立一個可以任意角度和潛器相交的傾斜水線面，利用初穩性水線面傾斜規律，盡快找到滿足要求的水線面。

(1) 假定一個水平吃水線面，建立假定水平吃水線剖面分析特征，獲得水線面形心(漂心)特征，如圖2所示。

(2) 建立通過水平吃水線面形心(漂心)的縱向中心軸。

(3) 建立通過縱向中心軸的橫傾水線面。

(4) 建立橫傾水線面的剖面分析特征，獲得水線面形心(漂心)特征。

(5) 建立通過橫傾水線面的形心(漂心)的橫向中心軸。

(6) 建立通過橫向中心軸的縱傾水線面即最終的傾斜水線面。

(7) 建立垂直于縱傾水線面的垂直面。

(8) 以最終的縱傾水線面為草繪平面，建立拉伸剪切特征，剪切后剩余部分為水下排水部件。拉伸特征草繪面積盡量是潛器水平投影面積的2倍，以保證大傾角下依舊可以完整剪切潛器模型，如圖3所示。

(9) 以最終縱傾水線面的法向為Z軸,最終縱傾水線面上沿潛器縱向為X軸,橫向為Y軸,建立水線面坐標系(坐標原點任意)。

圖3 水線面剪切特征及剪切后水面線坐標系

從以上步驟中建立的最終傾斜水線面的構造參數包括3個：水平吃水線的高度值；橫傾水線面的橫傾角度值；縱傾水線面的縱傾角度值。這三個變量可以確定滿足質量及質心約束的任意水線面。

5.3 建立分析特征

(1) 建立剪切后的結構重量分析特征，獲得排水結構質心(浮心)位置，如圖4所示。

圖4 浮心位置分析

(2) 在水線面坐標系下，測量排水部分結構浮心的橫向坐標和縱向坐標，以及給定重心的橫向坐標和縱向坐標，并建立分析特征，如圖5所示。

圖5 浮心重心在水線面坐標系下的坐標值

(3) 建立關系類型的分析特征，創建如浮心、重心橫縱坐標差值參數，給定質量與排水量之間的差值。如上幾步建立了排水量、浮心位置特征、重心位置特征，為了實現浮心和重心在水線面坐標系下X、Y值一致以及質量與排水量一致，建立他們的差值特征參數如圖6所示。

圖6 排水量、重心、浮心坐標比較分析特征

5.4 水線面確定

進入菜單欄分析模塊中的可行性/優化程序,選擇可行性模塊選項,設置約束及變量。采用GDP或MDS可行性分析方法, 在設計約束欄將浮心與重心坐標值差參數設置為0，排水量與質量差值設置為0，如圖7所示。

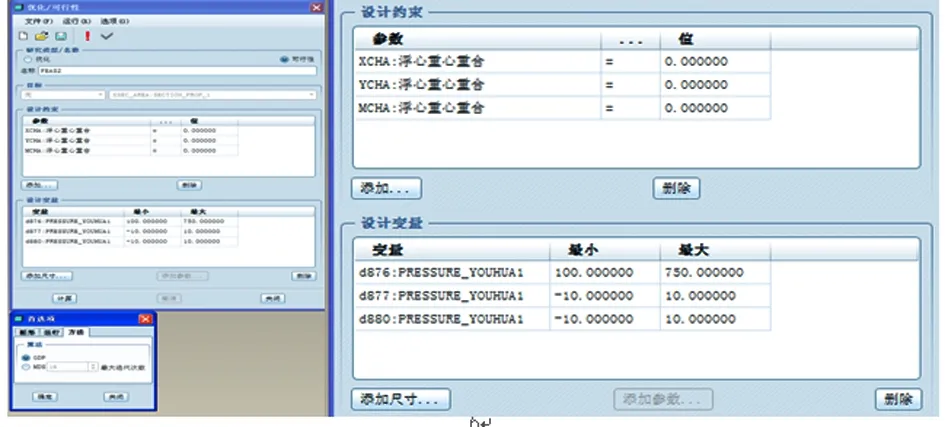
圖7 水線面可行性分析

經過迭代分析，在運行記錄欄出現“已找到可行解決方案”，并在模型上顯示符合要求的模型變量參數，水線面參數可行性分析結果如圖8所示。

圖8 水線面可行性分析結果

5.5 水面初穩性

6 靜穩性臂曲線求解

根據前文所述，潛器適用于大傾角理論求解穩性。為了尋找給定排水量下的靜穩性臂曲線即不同傾斜水線下浮心與重心的距離，基于上文PRO/E可行性分析方法，在吃水線坐標系下，約束排水量等于潛器質量，浮心、重心縱向位置重合，設計變量為吃水高度，水線面縱傾角，依次變換水線面的橫傾角度，計算記錄浮心與重心的橫向位置差，最后作圖畫出靜穩性臂曲線。具體步驟如下：

(1) 設置水線面橫傾角度為0°或其他初始角度；

(2) 進入關系模塊，設置約束條件和尺寸變量并進行關系式校驗，關系式設置如圖9所示；

圖9 建立敏感性分析關系式

[][]

(3) 應用敏感性分析功能，尺寸變量為橫傾角，變化范圍為0°～60°[6]，輸出變量為浮心與重心的橫向位置差，即得不同橫傾角下的靜穩性臂曲線，可將數據導入Excel表格繼續進行詳細數據圖線處理，如圖10、圖11所示。

圖10 PRO/E靜穩性臂曲線輸出

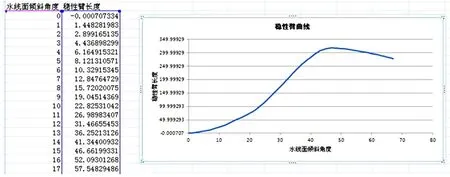
圖11 Excel靜穩性臂曲線輸出

7 結論

本文基于船舶穩性計算理論，應用PRO/E行為建模可行性與敏感性分析方法針對潛器三維模型的浮態與穩性進行智能化優化分析。由于迭代計算自動進行，浮心與重心坐標差值、排水量與重量差值收斂約束均為零，因此浮型與穩性計算效率與精度均比傳統水面船舶計算提高。本文水線面、靜穩性臂求解思路也可作為其他CAD軟件計算的參考。

[1] 盛振邦,劉應中.船舶原理[M].上海:上海交通大學出版社,2006,72-78.

[2] 徐建紅.基于數字型值表的船舶浮態穩性計算系統研究[D].大連:大連海事大學,2007.

[3] 張化英.利用計算軟件進行穩性復核需要注意的幾個問題[J].中國水運：下半月,2011,12：92.

[4] 郭仁生.基于Matlab和Pro/engineer優化設計實例解析[M].北京:機械工業出版社,2007.

[5] 魏艷春,蹇興東,史慶春.pro/e的行為建模技術[J].組合機床與自動化加工技術,2006,12:25-27.

[6] DNV Ship rules Pt.3 Ch.3.Hull Equipment and Safety[S].2011.

The PRO/E Model-based Stability Calculation of Submarine

SHI Zhan-xin

(Wuhan Second Ship Design and Research Institute, Wuhan Hubei 430064, China)

Determining the positions of waterline, buoyant centre and barycenter are the basics of submarine stability calculation. Based on the calculation theory of submarine stability, and combined with PRO/E 3D model of submarine, a new calculation method of submarine stability is explored by using the behavioral modeling technology. Compared with traditional calculation method, this automatism iterative calculation method is more efficient and accurate. The results can provide a reference for other stability calculation with CAD 3D software.

Submarine PRO/E behavioral modeling Stability

史戰新(1983-)，男，工程師。

U661

A