Banach空間上一類套代數的李環同構

鄧 娟，侯晉川，齊霄霏

(1. 太原理工大學 數學學院， 太原 030024；2. 山西大學 數學科學學院，太原 030006)

Banach空間上一類套代數的李環同構

鄧 娟1，侯晉川1，齊霄霏2

(1. 太原理工大學 數學學院， 太原 030024；2. 山西大學 數學科學學院，太原 030006)

令N,M分別是(實或復)數域F上的Banach空間X和Y上的套,具有性質: (0)和X都是N的極限點,即 (0)+=(0),X-=X. 令AlgN和AlgM分別為相應的套代數。證明了映射Φ:AlgN→AlgM是李環同構 (即Φ是可加、李可乘的雙射) 當且僅當Φ(A)=TAT-1+h(A)I對任意的A∈AlgN都成立, 或Φ(A)=-TA*T-1+h(A)I對任意的A∈AlgN都成立,其中h是在所有交換子上為零的可加泛函,T是可逆的有界線性或共軛線性算子。

Banach空間；套代數；李環同構

1 引言和主要結果

令R和S是兩個環, Φ:R→S是一個映射。如果對任意的A,B∈R, Φ(AB)=Φ(A)Φ(B), 稱Φ是可乘的; 如果對任意的A,B∈R, Φ([A,B])=[Φ(A), Φ(B)], 稱Φ是李可乘的, 其中[A,B]=AB-BA是A和B的李積, 也叫作交換子。進而, 如果Φ是雙射且李可乘的,稱Φ李可乘同構;如果Φ是雙射, 可加且李可乘的, 稱Φ李環同構。如果R和S是數域F上的兩個代數, Φ是雙射,F-線性的且李可乘, 稱Φ是李代數同構。對于環上的李環同構的研究, 參考[1- 3]和相關文獻。在這篇文章里我們重點關注Banach空間上的套代數間的李環同構的刻畫問題。

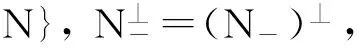
在文獻[6]中, Marcoux和Sourour證明了可分復Hilbert空間上的套代數間的李代數同構都可表示為α+β的形式, 其中α是代數同構或負的代數反同構,β: AlgN→CI是在所有交換子上為零的線性映射, 即對任意的A,B∈AlgN, 滿足β([A,B])=0. 要把這一結果推廣到任意Banach空間上套代數的情形,其主要困難之一是Banach空間的子空間不一定是可補的。

Qi和Hou在文獻[7]中通過刻畫某類Banach空間套代數之間的李可乘同構推廣了Marcoux和Sourour的結果。注意到, 李可乘同構不一定是可加的。令N,M分別是(實或復)數域F上的Banach空間X,Y上的套, 具有性質如果M∈M滿足M-=M, 則 M在Y中可補(明顯地, 如果Y是Hilbert空間或如果dimY<∞,這個假設是自然滿足的)。令AlgN和AlgM分別是相應的套代數, Φ:AlgN→AlgM是雙射。Qi和Hou在文獻[7]中證明了:如果dimX=∞, 且存在N中的非平凡元在X中是可補的, 則Φ是李可乘同構當且僅當存在映射h:AlgN→FI, 滿足對任意A,B∈AlgN,h([A,B])=0, 使得Φ(A)=TAT-1+h(A)I對任意的A∈AlgN都成立, 或Φ(A)=-TA*T-1+h(A)I對任意的A∈AlgN都成立。其中, 在第一種形式里,T:X→Y是可逆有界線性或共軛線性算子使得 N→T(N)是N到M上的序同構；而在第二種形式里,X,Y是自反的,T:X*→Y是可逆有界線性或共軛線性算子使得 N⊥→T(N⊥)是N⊥到M上的序同構。如果dimX=n<∞, 可以把套代數和上三角塊矩陣代數看成一樣, 則Φ是李可乘同構當且僅當存在域自同構τ:F→F, 可逆矩陣T使得要么Φ (A)=TAτT-1+h(A)對任意A都成立, 要么Φ(A)=-T(Aτ)trT-1+h(A)對任意A都成立, 其中對于矩陣A=(aij),Aτ=(τ(aij)),Atr是A的轉置。特別地, 上面的結果刻畫了有限維情形下的套代數之間的李環同構, 無限維情形, 套N和M滿足上面所提條件的套代數之間的李環同構, 以及任何Hilbert空間上套代數之間的李環同構。

最近, Wang和Lu在文獻[8]中從另外的角度推廣了Marcoux和Sourour的結果, 證明了Banach空間上的任意套代數AlgN和AlgM之間的李代數同構可以表示為α+β的形式, 其中α是代數同構或負的代數反同構,β: AlgN→FI是在每個交換子上為零的線性映射。因為對于套N有非平凡的可補元的情形下, 李代數同構在文獻 [9] 中已經得到刻畫, Wang和Lu在文獻[8] 中主要處理N中的所有的非平凡元都不可補的情形。

一個自然的問題是如何刻畫任意Banach空間上套代數之間的李環同構, 從而獲得比文獻[8]更一般的結果。本文的目的在套的最大元及最小元都是極限元, 即(0)+=(0),X-=X的條件下, 回答上述問題。注意, 李環同構和李代數同構是非常不同的。例如套代數間的代數同構總是連續的, 然而環同構在有限維情形不一定是連續的。

下面是本文的主要結果。

定理1令N,M是(實或復)數域F上的Banach空間X和Y上的套,AlgN和AlgM分別為相應的套代數。設(0)+=(0),X-=X, 則映射Φ:AlgN→AlgM是李環同構當且僅當存在套代數間的環同構或負的環反同構Ψ, 在所有交換子上為零的可加泛函h: AlgN→F, 使得Φ(A)=Ψ(A)+h(A)I對所有A∈AlgN都成立。

定理2令N,M是(實或復)數域F上的Banach空間X和Y上的套, AlgN和AlgM分別為相應的套代數。設(0)+=(0),X-=X, 則映射Φ:AlgN→AlgM是李環同構當且僅當存在可加泛函h:AlgN→F滿足對任意的A,B∈AlgN,h([A,B])=0, 且下列之一成立:

1) 存在有界可逆線性或共軛線性算子T:X→Y使得N→T(N)是N到M上的序同構, Φ(A)=TAT-1+h(A)I對任意的A∈AlgN都成立;

2)X,Y是自反的, 存在有界可逆線性或共軛線性算子T:X*→Y使得N⊥→T(N⊥)是N⊥到M上的序同構, Φ(A)=-TA*T-1+h(A)I對任意的A∈AlgN都成立。

進而, 如果F=R, 上述算子T是線性的。

注意到, 對于套N的假設條件(0)+=(0)和X-=X蘊涵X是無限維的。 本文第2部分給出預備引理, 它們中的一些也是證明主要結果中的一部分。第3部分給出主要結果定理1的證明。

2 預備引理

在這一部分, 我們給出一些預備引理, 定義和符號。它們在證明主要結果中要用到。

令X,Y是實或復數域F上的Banach空間,N,M是X和Y上的套, AlgN和AlgM分別是對應的套代數。我們知道套代數的交換子是平凡的, 即, 如果T∈B(X), 對任意算子A∈AlgN,TA=AT, 則T=λI,λ∈F。這個事實在本文中將不加解釋直接應用。另外, 符號ranT, kerT和rankT分別代表算子T的值域, 零空間和秩 (即, 值域ranT的維數)。對于x∈X,f∈X*,x?f表示X上秩不大于1的算子, 其定義為, 對于任意向量y, (x?f)y=f(y)x.有時候我們用〈x,f〉表示f在x處的值f(x).

下面引理是眾所周知的,它給出了套代數里一秩算子的刻畫。

對于任意非平凡元E∈N, 定義

J(N,E)=

{A∈AlgN:AE=0且A*E-1=0}.

(1)

在文獻[8]中, Wang和Lu證明了L是AlgN中的真極大交換李代數理想當且僅當存在唯一E∈N,L=FI+J(N,E). 下面的引理證明了任意極大交換李環理想也是這種形式。

引理2J是AlgN中的真極大交換李環理想當且僅當它是真極大交換李代數理想。

證明假設J是極大交換李環理想,則對任意A∈AlgN,C∈J和λ∈F, 我們有 [A,λC]=λ[A,C] ∈FJ, 這蘊含了FJ是李環理想。明顯地,FJ也是可交換的。 因為J是極大的,因此FJ?J. 而J?FJ. 因此我們有FJ=J. 從而J也是李代數理想。反過來是明顯的。 證畢。

(2)

利用上面引進的符號和類比(文獻[8]中引理 4.1, 4.3, 4.4)的論證, 我們能證明下面的引理對于李環同構仍然是正確的。

是非平凡的}→

∪{J(M, F):F∈M是非平凡的}

(3)

類似于文獻[8]中引理4.2, 我們有

下面的引理是顯而易見的。

引理5Φ(FI)=FI.

最后, 我們給出一個引理, 它在證明我們主要結果時要用到。令E,F分別是X和X*上的子空間。 用E?F表示集合{x?f:x∈E,f∈F}. 設W,V是數域F上的線性空間,τ是F的域自同構, 如果可加映射S:W→V滿足S(λx)=τ(λ)Sx對所有的x∈W,λ∈F都成立, 則稱S是τ-線性的。

引理6令Xi是無限維Banach空間,i=1,2. 令Ei,Fi分別是Xi,Xi*的維數>2的閉子空間。令Ai是包含Ei?Fi的B(Xi)和恒等算子I的子代數。假設Ψ:A1→A2是滿足 Ψ(FI)=FI和Ψ(FI+E1?F1)=FI+E2?F2的可加雙射, 則存在映射γ:E1?F1→F, 域自同構τ:F→F使得要么

1) 對任意的x∈E1,f∈F1,Ψ(x?f)=γ(x,f)I+Cx?Df, 其中C:E1→E2,D:F1→F2都是τ-線性雙射; 要么

2) 對任意的x∈E1,f∈F1,Ψ(x?f)=γ(x,f)I+Df?Cx, 其中C:E1→F2, D:F1→E2都是τ-線性雙射。

引理6的證明類似文獻[11]中的方法可以得到, 此處省略。

3 主要結果的證明

Φ(A((x?f)B)=Φ([A,[(x?f,B]])=

[z?g,[R,u?h]]=(z?g)R(u?h)=0.

由Φ的單射性得到A((x?f)B=0, 這蘊含A(x?f)=0或者 (x?f)B=0. 如果A(x?f)=0, 則0=Φ([A,x?f])=[z?g,R]=(z?g)R≠0, 矛盾; 如果 (x?f)B=0, 則 0=Φ([x?f,B])=[R,u?h]=R(u?h) ≠ 0, 矛盾。

Φ(B((x?f)A)=Φ([B,[x?f,A]])=

[u?h,[R,z?g]]=(z?g)R(u?h)=0,

下面我們給出定理1的證明。

E∈N, Φ(FI+E? E⊥)=

因此, 由引理6, 存在環同構τE:F→F和映射γE: E? E⊥→F使得要么

Φ(x?f)=γE(x,f)I+CEx?DE⊥f. (4)

Φ(x?f)=γE(x,f)I+DE⊥f?CEx.(5)

容易驗證, 如果存在非平凡元E0∈N使得等式(4)成立, 則等式(4)對任意非平凡元 E∈N成立; 如果存在非平凡元E0∈N使得等式(5)成立, 則等式(5)對任意非平凡元E∈N成立。

假設等式(4)對非平凡的元E∈N成立。則對任意N∈N,x∈E∩N,f∈E⊥∩N, 我們有

Φ(x?f)=γE(x,f)I+CEx?DE⊥f=

γN(x,f)I+CNx?DN⊥f.

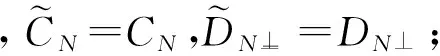
到現在為止,我們已經證明了:存在τ-線性雙射C: ∪{N∈N: N≠ (0),X}→∪{M∈M: M≠ (0),Y},D: ∪{N⊥: N∈N, N≠ (0),X}→∪{M⊥: M∈M, M≠ (0),Y}以及映射 γ: ∪{E? E⊥:E∈N{(0),X}}→F使得對任意x∈N,f∈N⊥, N∈N{(0),X}, 我們有

Φ(x?f)=γ (x,f)I+Cx?Df.

(6)

因此, 對任意A∈AlgN,x∈N和f∈N⊥, 由等式(6), 我們有

Φ([A,x?f])=[Φ(A), Φ(x?f)]=

Φ(A) Cx?Df-Cx?Φ(A)*Df

和 Φ([A,x?f])=

Φ(Ax?f-x?fA)=(γ (Ax,f)-

γ (x,A*f))I+CAx?Df-Cx?DA*f.

結合以上兩個等式并且注意到I是無限秩的, 可以得到對任意N∈N{(0),X}以及x∈N,f∈N⊥, 我們有

Cx?Φ(A)*Df-Cx?DA*f=

Φ(A) Cx?Df-CAx?Df

成立。又注意到D是雙射, 所以存在標量h(A)使得對任意x∈∪{N∈N: N≠ (0),X}, 有

Φ(A) Cx=CAx+h(A)Cx.

(7)

顯然,h作為AlgN上的泛函是可加的。對任意A∈AlgN, 定義Ψ (A)=Φ(A)-h(A)I. 則由等式(7), 對任意A,B∈AlgN,x∈∪{N∈N: N≠ (0),X}, 我們有

Ψ(AB)Cx=CABx=

Ψ(A)CBx=Ψ(A) Ψ(B)Cx.

因為∪{N∈N: N≠ (0),X}在X中稠密且C是雙射, 于是對任意A,B∈AlgN, 有Ψ(AB)=Ψ(A)Ψ(B), 也就是說, Ψ是環同構并且對任意A∈AlgN, Φ(A)=Ψ (A)+h(A)I.

類似地,如果等式(5)成立, 容易驗證, 存在環反同構Ψ: AlgN→AlgM及可加泛函h: AlgN→F, 使得Φ(A)=-Ψ(A)+h(A)I對所有A∈AlgN都成立。

到此定理得證。

[1] Beidar L I, Martindale W S Ⅲ， Mikhalev A V.Lie isomorphisms in prime rings with involution[J]． J Algebra, 1994,169(1)：304-327.

[2] Bresar M. Commuting traces of biadditive mappings, commutativity preserving mappings and Lie mappings[J]． Trans Amer Math Soc, 1993,335(2)： 525-546.

[3] Martindale W S Ⅲ.Lie isomorphisms of prime rings[J]．Trans Amer Math Soc, 1969,142：437-455.

[4] Davidson K R. Nest Algebras, Pitman Research Notes in Mathematics[M]． London, New York:Longman, 1988.

[5] Longstaff W E.Operator of rank one in reflexive algebras[J]．Canad J Math, 1976(28)：19-23.

[6] Marcoux L W,Sourour A R. Lie isomorphisms of nest algebras[J]． J Func Anal, 1999,164(1)：163-180.

[7] Qi X F, Hou J C.Characterization of Lie multiplicative isomorphisms between nest algebras[J]． Sci China Math, 2011，54(11)：2453-2462.

[8] Wang T, Lu F Y.Lie isomorphisms of nest algebras on Banach space[J]． J Math Anal Appl, 2012,391(2)：582-594.

[9] Benkovic D, Eremita D. Commuting traces and commutativity preserving maps on triangular algebras[J]． J Algebra, 2004,280(2)：797-824.

[10] Hou J C, Zhang X L. Ring isomorphisms and linear or additive maps preserving zero products on nest algebras[J]. Linear Algebra and its Applications, 2004,387(1):343-360.

[11] Bai Z F, Hou J C, Du S P.Additive maps preserving rank-one operators on nest algebras[J]． Lin Multi Algebra, 2010，58(3)：269-283.

(編輯：朱倩)

LieRingIsomorphismsbetweenCertainNestAlgebrasonBanachSpaces

DENGJuan1,HOUJinchuan1，QIXiaofei2

(1.CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China；2.CollegeofMathematicalSciences,ShanxiUniversity,Taiyuan030006,China)

LetNandMbe nests on Banach spacesXandYover the (real or complex) fieldF, with the property that both (0) andXare limit points ofN, i.e., (0)+=(0) andX-=X. Let AlgNand AlgMbe the associated nest algebras, respectively. It is shown that a map Φ:AlgN→AlgMis a Lie ring isomorphism (i.e., Φ is additive, Lie multiplicative and bijective) if and only if Φ(A)=TAT-1+h(A)Ifor allA∈AlgNor Φ(A)=-TA*T-1+h(A)Ifor allA∈AlgN, wherehis an additive functional vanishing on all commutators andTis an invertible bounded linear or conjugate linear operator.

Banach spaces;nest algebras;Lie ring isomorphisms

2013-04-10

國家自然科學基金資助項目 (11171249, 11101250, 11271217)

鄧娟(1986-)， 女, 湖北荊門人，碩士，主要從事算子理論與算子代數研究，(E-mail)juanhappyforever@163.com

侯晉川，博士，教授，博導，(E-mail)houjinchuan@tyut.edu.cn

1007-9432(2014)01-0133-05

O177.1

:A