一類具有黏阻尼的非線性彈性桿方程的初邊值問題
牛麗芳,張建文
(太原理工大學 數學學院,太原 030024)
一類具有黏阻尼的非線性彈性桿方程的初邊值問題
牛麗芳,張建文
(太原理工大學 數學學院,太原 030024)
在給定的Sobolve空間中,研究了一類非線性彈性桿方程的初邊值問題,其中非線性項具有臨界增長指數。描述了考慮非線性勢力作用下具有黏阻尼的彈性桿的振動問題,利用Faedo-Galerkin方法,通過對變系數及非線性的處理,證明了該系統在一定初邊值條件下整體弱解的存在、唯一性。為此類力學振動問題的研究和計算提供了理論依據。
Faedo-Galerkin方法;黏阻尼;非線性彈性桿;初邊值問題
具有粘阻尼的非線性彈性桿的振動問題是動力系統中最常見又非常復雜的問題之一,如果考慮非線性勢力作用,可建立如下數學模型
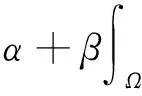
δΔut-ωΔutt=f(u),x∈Ω,
(1)

尚亞東[1]研究了系統當α=1,β=γ=0,ω=1,n=1,2,3時整體強解的存在、唯一性,僅得到了f(u)是次臨界Sobolve指數情形下整體強解的存在、唯一,而f(u)缺乏緊性。張宏偉[2]在文獻[1]的基礎上,利用位勢井方法,研究了非線性項f(u)具有臨界指數增長時系統整體弱解的定性問題。之后謝永欽[3]研究了此系統的長時間行為,以及當α=1,β=γ=0,δ=1時系統的漸近行為。文獻[5]在前人的基礎上研究了當α=1,β=γ=0時,系統帶有記憶項時整體動力學行為。
筆者研究當δ=1時,方程組在初始條件
u(x,0)=u0(x),ut(x,0)=u1(x),
?x∈Ω,
(2)
及邊界條件
u(x,t)=u(2)(x,t)=0,
?x∈?Ω,t∈[0,T]
(3)
下整體強解的存在性、唯一性。
1 預備知識






引理2[6]設f∈L∞(0,T),k≥0,c0為常數,若對一切t∈[0,T],

則f(t)≤c0ekt.
2 整體弱解的存在性、唯一性
本節我們將利用Galerkin方法,結合能量估計,研究系統(1)—(3)的整體弱解,對非線性項f(s)做一些約束,假設f(s)滿足:

(h2) |f′(s)|≤c0(1+|s|p), ?s∈.

f(s)s≤λs2+c1, ?s∈,
(4)
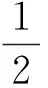
(5)

使得

um(t)滿足逼近方程
(6)
及初始條件
um(0)=u0m=

(7)
umt(0)=u1m=

(8)
注意到系統(6)—(8)是關于函數aj(t)(j=1,2,…,m)的二階非線性常微分方程組的柯西問題,由常微分方程理論知:?tm>0,使得系統(6)—(8)的解存在,從而得um(t).
引理3設Ω?n是有界光滑區域非線性項f(s)滿足條件(h1)-(h2),則對任一T>0及系統(4)—(6)的任意解um(x,t),umt(x,t)滿足:
‖umt‖2+‖um‖2≤M1, 0≤t≤T.
(9)
其中M1是與m無關的常數。
證明在(6)中取φ=umt,得
(10)
故
即 |umt|2+α‖um‖2+

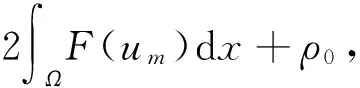
其中
ρ0=|umt(x,0)|2+α‖um(x,0)‖2+

由(5)及Poincareé不等式得

ω‖umt‖2≤ρ0+Cm(Ω)ρ.
(11)
其中C為與m無關的常數,本文不同地方的C代表不同的與m無關的正常數。
由(7)、(8)及f的連續性,存在正常數M1(M1與T及t無關),對一切m均有
ρ≤M1,‖umt‖2+‖um‖2≤M1,
?0≤t≤T.
(12)
證畢。
引理4設Ω?n是有界光滑區域非線性項f(s)滿足條件(h1)-(h2),則對任一T>0及系統(4)—(6)的任意解um(x,t)滿足:
‖umtt‖2+|umtt|2≤M2, 0≤t≤T.
(13)
其中M2是與m無關的常數。
證明在(6)中取φ=umtt,得




(14)
由條件(h2)有
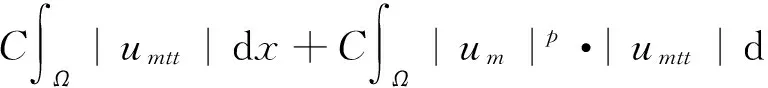
再由Young不等式得:
‖um‖2p+
ρ1(|umtt|2+‖umtt‖2),
(15)

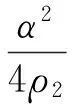
(16)

C‖um‖2+ρ3‖umtt‖2,
(17)

C(‖um‖2+‖umt‖2)+ρ4‖umtt‖2,
(18)

C‖umt‖2+ρ5‖umtt‖2.
(19)

‖umtt‖2+|umtt|2≤M2, 0≤t≤T.
證畢。
定理1設Ω?n是有界光滑區域非線性項f(s)滿足條件(h1)-(h2),則系統(1)—(3)存在如下意義的整體弱解u(x,t):
?T>0,u(x,t),ut(x,t),
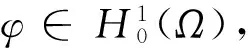
證明由引理1,2及(10)式知

因為可分賦范線性空間的一致有界線性泛函序列中必可取一個弱星收斂的子列,故可取{um},{umt},{umtt}的子列{uμ},{uμt},{uμtt},使得
uμ(x,t)→u(x,t),

(20)
uμt(x,t)→ut(x,t),

(21)
uμtt(x,t)→utt(x,t),

(22)
f(uμ)→χ,在Lq(Ω×[0,T])中弱收斂。
(23)
由(15)式、條件 (h2)及引理1,存在僅依賴于c0和M1的正常數M3,使得
?μ∈,t∈[0,T].
其中
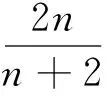
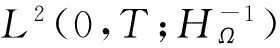
φ(x,t)dxdt=
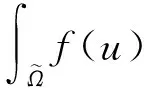



由(20)—(21),有
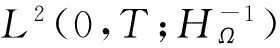
又由于
故 Δuμtt(x,t)→Δutt(x,t)
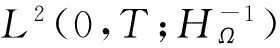

(24)
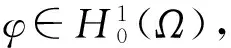
下面驗證u(x,t)滿足初值條件
在(24)中取ψ=v(t),則有

(25)
對(25)式中第一項作兩次分部積分,得


(26)
同理可得:


再由(7)—(8),(20)—(23)得:


(u1,v(0)).
(27)
比較(26)和(27),并由v(0),vt(0)的任意性得:
因此u(x,t)為系統(1)—(3)滿足初邊值條件的一個整體弱解。
定理2設Ω?n是有界光滑區域非線性項f(s)滿足條件(h1)-(h2),則系統(1)—(3)的整體弱解是唯一的,且對任意兩個解存在η>0,?t>0,有‖‖≤M4eη t,其中‖‖2+ω‖‖2.
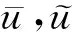
(28)
(29)
(30)
用ut與(28)式在L2(Ω)中作內積,得

‖ut‖2+I1=

(31)
其中
由引理3,條件(h2)及Sobolev嵌入定理,得

?t∈[0,T].
其中常數M(T)僅依賴于T和初值,0≤θ≤1,故

C(‖u‖2+‖ut‖2).
(32)
下面對I1進行估計。記

因為




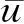

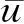
并由引理1和引理3,有

利用Young不等式得:
I2≤C(‖u‖2+|ut|2).
(33)


同理因為






C(‖u‖+|ut|).
利用Young不等式得
I3≤C(‖u‖2+|ut|2).
(34)
由(33)—(34),得
I1≤C(‖u‖2+|ut|2).
(35)
綜合(31)、(32)、(35),存在常數,使得C1

C1(|ut|2+α‖u‖2+ω‖ut‖2).
于是有
|ut|2+α‖u‖2+ω‖ut‖2≤M4eη t,
?(x,t)∈Ω×(0,T).

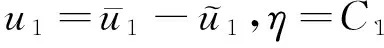
則

(36)
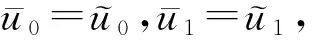
3 結論
通過論證,得到了一類具有黏阻尼的非線性彈性桿方程在齊次邊界條件下整體弱解的存在、唯一性。工程中能夠簡化到與本文模型有相同受力情況及邊界約束的模型時,從理論上可采用該方程對工程進行估算,并能對結構的強度、穩定性有一定的了解,為安全經濟地進行結構設計提供了指導。
[1] 尚亞東. 方程utt-Δu-Δut-Δutt=f(u)的初邊值問題[J].應用數學學報,2000,23(3):385-393.
[2] 張宏偉,呼青英. 一類非線性雙曲方程整體弱解的存在性和不存在性[J]. 工程數學學報,2003,20(3):131-134.
[3] Xie Yongqin, Zhong Chengkui. The existence of global attractors for a class nonlinear evolution equation [J]. Math Anal Appl, 2007(336):54-69.
[4] Xie Yongqin, Zhong Chengkui. Asymptotic behavior of a class of nonlinear evolution equations[J]. Nonlinear Analysis, 2009(71):5095-5105.
[5] 牛麗芳,張建文,張建國. 一類帶記憶項的非線性彈性桿的全局吸引子[J]. 數學的實踐與認識,2013,43(18):262-268.
[6] Ball J M. Initial-boundary value problems for an extensible beam [J]. Mathe Anal, 1973(42): 61-88.
(編輯:張紅霞)
Initial-boundaryValueProblemsforaKindofNonlinearElasticRodswithSomeSuitableDamped
NIULifang,ZHANGJianwen
(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)
The initial-boundary value problem was studied in given Sobolve space, where the nonlinear term satisfies a critical exponential growth condition. The problem involves a class of nonlinear partial differential equations describing the nonlinear elastic rods with viscous damp under external force. By using Faedo-Galerkin method, the existence and uniqueness of the weak solutions for the proposed problem were proved through the appropriate manipulation of variable coefficient and nonlinear items.
Faedo-Galerkin method; viscous damp; nonlinear elastic rods; initial-boundary value problems
2013-02-09
國家自然科學基金資助項目(11172194);國家自然科學基金數學天元青年基金資助項目(11226316);山西省青年科技研究基金資助項目(2011021002-2);山西省自然科學基金資助項目(2010011008)
牛麗芳(1980-),女,山西晉城人,博士生,講師, 主要從事動力系統研究,(Tel)13403406995
張建文,男,博士,教授,博導,(E-mail)zhangjianwen@tyut.edu.cn
1007-9432(2014)01-0128-05
O19
:A

