“三關系法”在扭轉與彎曲分析中的應用

張 睿 智

(中國礦業大學(北京)資源與安全工程學院，北京 100083)

“三關系法”在扭轉與彎曲分析中的應用

張 睿 智

(中國礦業大學(北京)資源與安全工程學院，北京 100083)

對“三關系法”即變形幾何關系、應力應變關系、靜力學關系進行了名詞闡釋，介紹了“三關系法”在扭轉與彎曲中的分析方法，并結合實例作了說明，有助于實際工作及學習的參考應用。

變形，應力，靜力，關系，扭轉，彎曲

扭轉與彎曲來自于材料力學中最基本的兩種力的形式：剪切與拉壓，是構成復雜材料變形的最簡單變形形式。可以說，想學好材料力學這座高堂廣廈，扭轉與彎曲的地位就好比地基一般。同樣，在校核材料強度上，對扭轉和彎曲的應力求取是必不可少的，然而較之于一般的剪切應力和拉壓應力的定義式求法，前者或需要更縝密的分析和計算。本文即將用“三關系法”向讀者介紹求取這兩種應力的分析方法。所謂“三關系法”即“變形幾何關系—應力應變關系—靜力學關系”分析方法。需要說明的是，在如今的高等院校中，學生傾向于直接死記硬背求解應力的公式，對推導過程一知半解，而實際上，了解求取過程有助于同學理解和記憶公式，同時掌握最根本的有限元分析法也是步入實際場景、進入現實工作當中必不可少的技能。

1 名詞釋義

1)變形幾何關系。變形幾何關系的研究對象是從變形體上截取的順應變形的有限元，同樣遵循平截面假設和圣維南原理。我們將根據其變形前后在特定方向上的角度和長度變化得到應變表達式。

2)應力應變關系。應力應變關系即胡克定律，它將應力與應變結合起來，通過應變得到應力。在這里，扭轉用到剪切胡克定律τ=Gγ，彎曲用到胡克定律σ=Eε。

3)靜力學關系。靜力學關系是通過對微元力的積分與力偶矩建立關系，并引入慣性矩的概念，最終將不可求的微元素轉化為可求解的量，是對胡克定律建立起的應力表達式的完善。

2 “三關系法”在扭轉與彎曲中的分析方法

1)“三關系法”在扭轉中的分析方法。

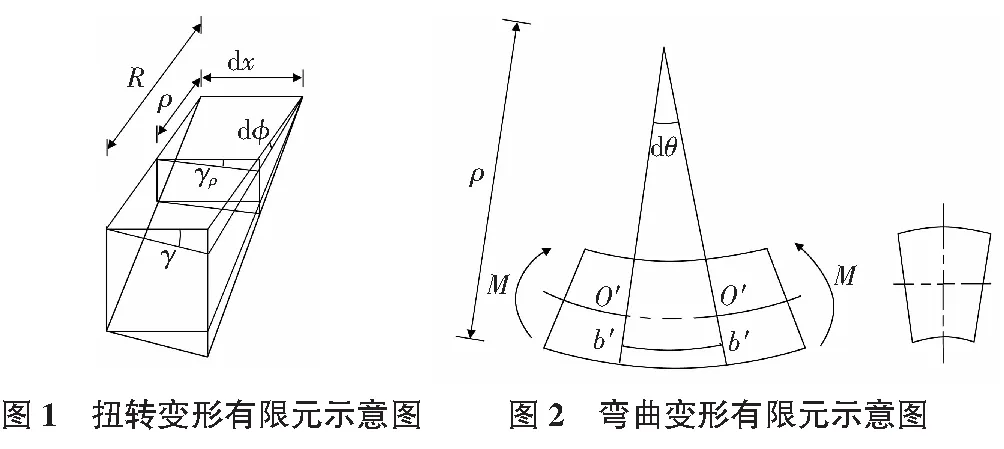
a.變形幾何關系。如圖1所示為一僅受扭轉的軸的單元體，在距軸線為ρ的地方，根據幾何關系其切應變為：

γρdx=ρdφ。

即：

(1)

b.應力應變關系。切應力與切應變服從剪切胡克定律：

τ=Gγ

(2)

將式(1)代入式(2)可以求得距軸線為ρ處的切應力為:

(3)

c.靜力學關系。圓軸扭轉時，平衡外力偶矩的扭矩是由橫截面上無數的微剪力組成的。各微剪力對軸線之矩的總和，即為該截面上的扭矩，即：

T=∫AρτρdA

(4)

將式(3)代入式(4)得：

(5)

將式(5)代入式(3)得:

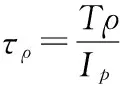
隨即得到剪切應力公式。

2)“三關系法”在彎曲中的分析方法。

a.變形幾何關系。取微段梁來分析，其變形后的情況如圖2所示。現研究距中性層y處縱向纖維b′b′的變形。

縱向線應變為:

(6)

b.應力應變關系。正應力與線應變的關系服從胡克定律：

σ=Eε。

將式(6)代入得：

(7)

c.靜力學關系。確定中性軸的位置和曲率：

y軸為對稱軸；z軸為中性軸，其位置暫未知；x軸為過原點且平行于軸線(見圖3)。

(8)

將式(7)代入式(8)得:

(9)

將式(9)代入式(7)得:

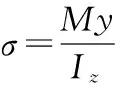
隨即得到彎曲應力公式。

3 典例分析

以“三關系法”在扭轉中的應用，我們來計算工程中常用的“U”形梁的剪切應力(如圖4所示)，已知梁所受的扭矩T以及它的尺寸。

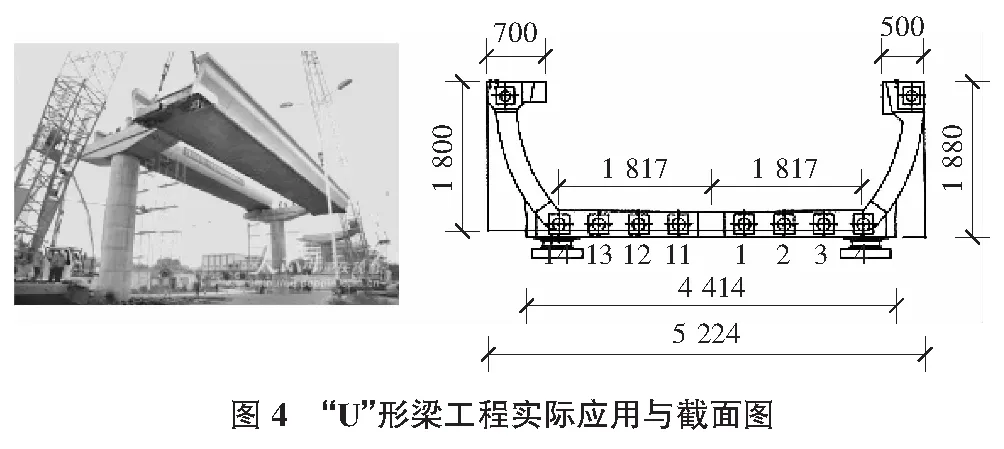
1)變形幾何關系。將“U”形梁補充成為截面為圓的梁，則其有限元同圖1，應變表達式不變，如下：

γρdx=ρdφ。

即：

(10)

2)應力應變關系。切應力與切應變服從剪切胡克定律：

τ=Gγ

(11)

將式(10)代入式(11)可以求得距軸線為ρ處的切應力為：

(12)

3)靜力學關系。取截面上的微剪力，同樣積分得到扭矩表達式：

T=∫AρτρdA

(13)

將式(12)代入式(13)得:

(14)

將式(14)代入式(12)得:

(15)

現在，只需把ρ關于圖4截面的函數用MATLAB擬合出來，然后求積分∫AρdA，把結果代入式(15)即可。

4 結語

關于異形梁的應力的求取我們可以采用“三關系法”，即變形幾何關系—應力應變關系—靜力學關系。這種方法有效規避了學生死記硬背公式在實際場景中的尷尬，強化知識的理解，強調運用，是互動—啟發式教育的典型學習、分析方法。

[1] 北京科技大學,東北大學.工程力學材料力學[M].北京：高等教育出版社,2008.

[2] 宮偉力,趙帥陽,彭巖巖.工程力學的互動啟發式教學法探討[J].科教文匯,2014(270)：49.

On application of “three-relation method” in analysis of torque and flexural loads

ZHANG Rui-zhi

(SchoolofResourcesandSafetyEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)

The paper introduces and interprets the “three-relation method”, including the geometrical relationship of deformation, the stress-strain relationship and the statics relation, introduces the analysis method of the method in the torque and flexural loads, and indicates by adopting some examples, so as to provide some reference for its application in work and study.

deformation, stress, statics, relation, torque, flexural load

1009-6825(2014)17-0047-02

2014-04-05

張睿智(1993- )，女，在讀本科生

TU311

A