一道“北約”自主招生試題的探究與推廣

●

(棗莊市第三中學 山東棗莊 277100)

題目

求證：tan3°是無理數.

(2014年“北約”自主招生數學試題)

命題1

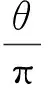
預備定理

命題2

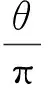
證明

cosnθ=cosmπ=(-1)m.(1)

對于任意正整數n,2cosnθ可以表示為2cosθ的n次整系數多項式，且首相系數為1，即

2cosnθ= (2cosθ)n+a1(2cosθ)n-1+…+

an-1(2cosθ)+an,

(2)

其中a1,a2,…,an都是整數.

式(2)運用歸納法容易證明：當n=1時，2cosθ=2cosθ；當n=2時，2cos2θ=(2cosθ)2-2.假設式(2)對n及n+1已成立，則

2cos[(n+2)θ]=2cosθ·2cos[(n+1)θ]-2cosnθ.

這表明，式(2)對于n+2也成立.

由式(1)、式(2)及已知條件可知，x=2cosθ是方程

xn+a1nn-1+…+an-1x+an-2(-1)m=0

(3)

下面證明命題1：

證明

從而

得

于是