新型離散自適應變結構算法在步進梁控制中的應用

魯照權 周 俊

(合肥工業大學電氣與自動化工程學院，合肥 230009)

步進梁輸料過程中，由于移動梁本身加上所運的鋼坯有數百噸之重，使得移動梁的周期性步進運動具有大慣性特點；由于流量、壓力變化及泄漏等因素，使得液壓傳動機構具有非線性特性。因此步進梁被控對象具有大慣性、非線性及變結構的特點。針對非線性被控對象，被提起最多的是變結構控制，從本質上說，變結構控制是一種非線性系統反饋控制，在系統面對外界的擾動(包括自身的參數攝動)時能很好地通過自身的非線性自適應函數調整控制律使得系統具有不變性。目前討論較多的是連續時間系統，并且已有了很多變結構方面的理論成果，但是隨著計算機技術的發展，特別是DSP技術的成熟，對離散時間系統變結構控制的要求越來越高[1]。通過將連續的趨近律離散化就產生了各種離散趨近律控制策略，最初提出的指數趨近律設計離散變結構控制，使系統表現出一定的魯棒性，但缺點是系統狀態接近滑動模態面時易產生抖振且不能收斂于原點[2]。之后很多學者在此基礎之上提出了一些改進的趨近律，主要思路是在指數趨近律中引入非線性函數來解決兩個問題：系統的狀態如何從任意的初始位置快速地逼近滑動模態面；系統狀態如何能夠以弱小的抖動最終收斂于原點。恒速趨近律解決不了這兩個問題之間的矛盾，在滿足快速性逼近的同時無法保證抖動弱小，因此后續的變速趨近律分別針對兩種不同階段采取不同的趨近律進行切換，然而由于切換條件難以確定，再加上切換可能導致系統產生不可預知的抖動，后續又有人引入了一種實數范圍內可導有界的雙曲正切函數，較好地解決了上述切換過程中平滑過渡的問題，同時在趨近律中結合了擾動上限的補償[3]，但是在進入準滑動模態區之后未能針對抖動的振幅進行有效的限定，導致在系統受到抖動較大的擾動時，無法起到較好的消抖作用。文獻[4]提出了一種基于自適應切換增益的變結構離散控制，能夠根據不確定擾動項的大小來自適應調整切換增益，但是趨近律的設計中卻并沒有充分考慮到平滑過渡問題。筆者正是結合了上述兩種方法的優點，設計了一種趨近律既能快速地從任意初始狀態趨向于準滑動模態面并收斂于原點，又能根據擾動不確定項上確界來自適應調整增益達到變結構控制中消抖的目的。①

1 電液伺服系統的組成

電液比例伺服控制系統的組成如圖1所示，系統主要包括控制器、伺服放大器、伺服閥和液壓缸。本項目背景是基于山東臨沂軋鋼廠的加熱爐步進梁運動控制系統，以PLC為控制核心，通過332模塊完成數模轉換和信號放大，并輸出控制電壓，現場的開環控制優點在于步進梁在輸送500t以上的鋼坯負載時無振蕩，但是低精度的位移和機械延遲使得系統在每一個步進周期中都要進行頻繁的步距調整，無法保證出料端的鋼坯能夠無偏差地放于出料輥端[5]。改進的基于電液比例伺服控制系統的閉環控制系統采用RHM-MD70S1G3100型磁致伸縮位移傳感器來提供同步實時的活塞絕對位移輸出。通過SSI接口完成與控制器的數據通信，為閉環控制提供反饋通道。

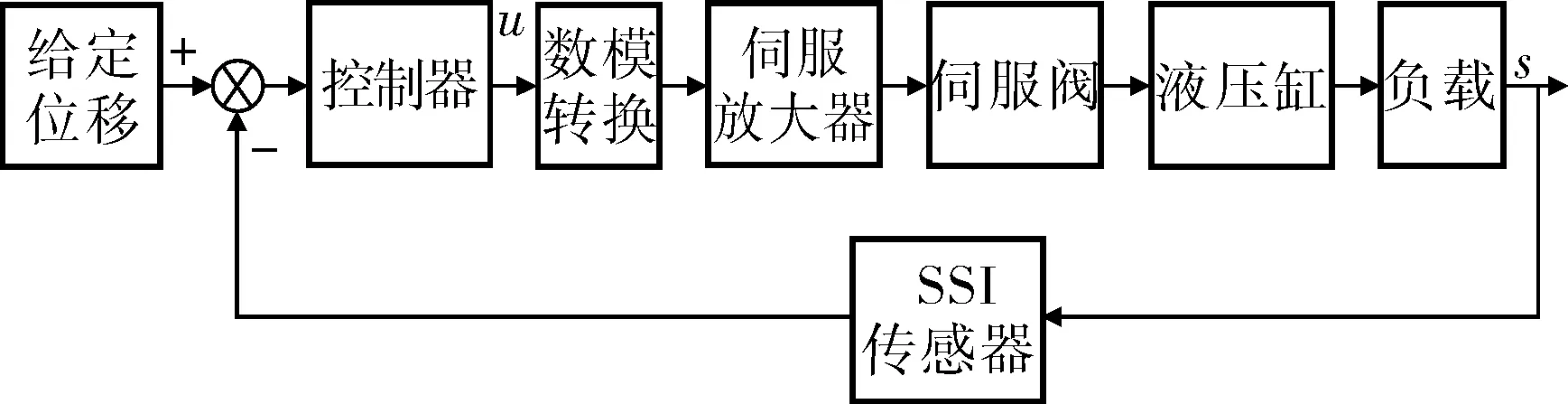
圖1 電液伺服控制系統組成框圖

2 電液伺服系統的離散線性數學模型

考慮到伺服放大器和伺服閥的動態遠高于系統的負載響應，將伺服放大器和伺服閥等效成比例環節，設兩者的增益依次為Kv、Ksv。圖2為電液伺服控制系統原理示意圖，采用零開口的四邊滑閥，4個節流窗口是匹配和對稱的，因為活塞中有桿腔與無桿腔的面積大小不同，因此在活塞外伸與內縮時系統的模型是有差異的。限于篇幅，筆者只討論活塞外伸的情況。

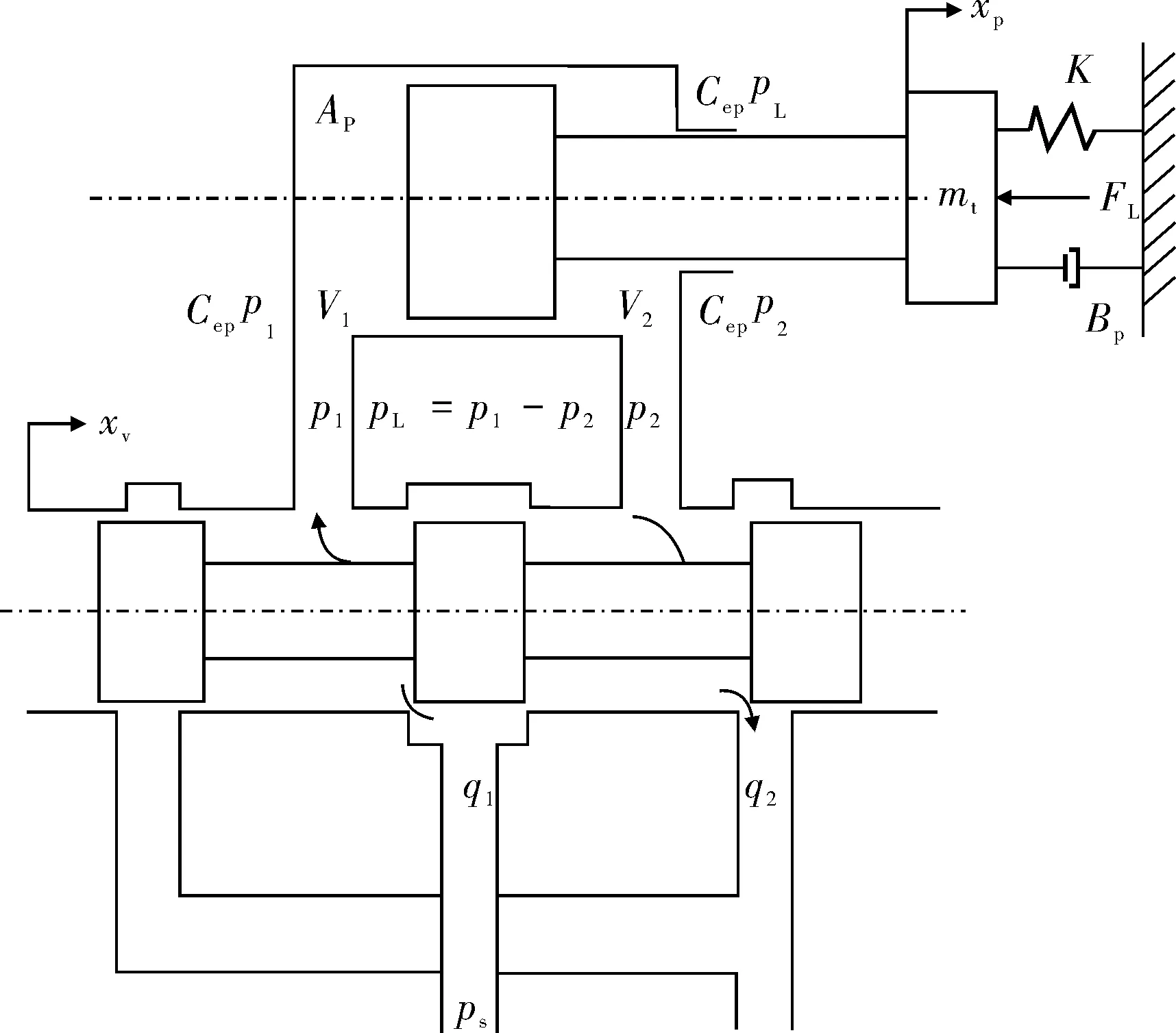
圖2 四邊滑閥控制下的非對稱液壓缸模型示意圖Ap——液壓缸活塞有效面積； Bp——活塞以及負載的粘性阻尼系數； Cep——液壓缸外泄漏系數； Cip——液壓缸總泄漏系數； FL——作用在活塞上的任意外負載力； K——負載彈簧剛度； mt——活塞和負載以及整個活塞上連接一起的附件總質量；p1、p2——無桿腔、有桿腔油液壓力； pL——控制缸兩腔壓力差值絕對值；q1、q2——液壓缸進油、回油流量;V1、V2——無桿腔、有桿腔體積； xv——液壓缸位移。

采用恒壓變量柱塞泵為系統提供油源壓力，故在此假定油源壓力ps恒定，回油壓力p0為零，為了忽略管道中的壓力損失和管道動態，假定閥與液壓缸的連接管道對稱且短而粗，并且假定液壓缸每個工作腔內各處壓力相等，油溫和體積彈性模量為常數，介質油液是不可以壓縮的，液壓缸內、外泄漏均為層流流動，閥的各節流口流量系數相等[6]。

基于以上假設，電液伺服閥的線性化流量方程為：

qL=Kqxv-KcpL

(1)

式中Kc——流量-壓力系數；

Kq——流量增益；

qL——系統負載流量。

利用液壓缸的流量連續方程可以求得：

(2)

式中xp——活塞位移；

Vt——總壓縮容積；

βe——有效體積彈性模量。

液壓缸和負載的力平衡方程為：

(3)

將式(1)～(3)化解合并并進行拉氏變換，可得：

(4)

最終可求得：

Xp=

(5)

y=xpsinθ

(6)

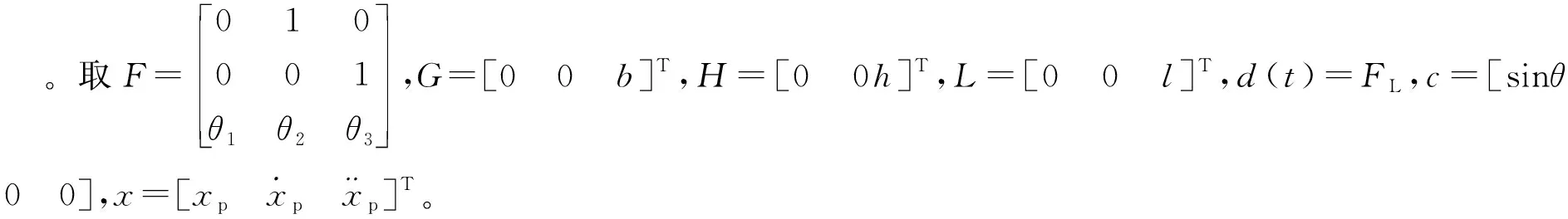
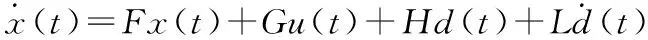
y=cx

(7)

式(7)的通解為：

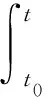
(8)

設控制力零階保持，即：

u(t)=u(kT),kT≤t≤(k+1)T

(9)

其中T為采樣周期，取t0=kT，可知u(τ)在上述區間恒為常數u(kT)，得：

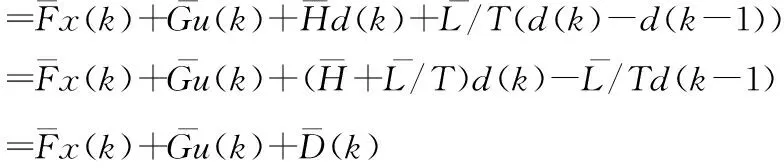
y(k)=cx(k)

(10)

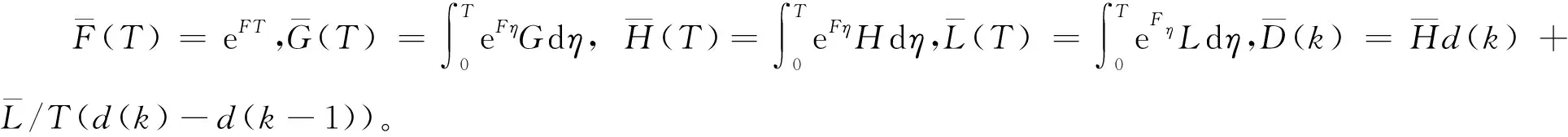
3 離散趨近律的設計

對于式(10)表示的離散非線性系統取切換函數為：

s(k)=Cx(k)

(11)

其中x(k)∈R3×1，令s(k)=Cx(k)=0。由式(11)得到系統的滑動模態面，對于變結構設計的內容，按照不同的運動階段分為兩個部分：設計離散趨近律使得系統從任意初始狀態出發都可以快速趨近滑動模態面；確定C的值，使得系統到達滑動模態面之后能夠保持良好的動態性能。對于離散趨近律的設計，文獻[3]通過引入tansigx函數，巧妙地解決了變速趨近律在遠近切換中帶來的不穩定抖動問題，趨近律如下：

s(k+1)=(1-qT)s(k)-εTtansig(‖x‖)sgn(s(k))

(12)

其中ε、T、q分別為到達速度、采樣周期和趨近速度參數。

當‖x‖→+∞時有：

(13)

式(12)變為：

s(k+1)=(1-qT)s(k)-εTsgn(s(k))

(14)

即典型的指數趨近律(Exponential Reaching Law)。當‖x‖→0時，依據洛必達法則有：

(15)

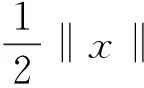
(16)

即典型的變速趨近律。當系統從距離原點較遠的初始狀態開始運動至滑動模態面的過程中，函數的連續可導性質使得指數與變速趨近律的切換過程平穩，而且最終在原點收斂。缺點是該方法并沒有充分考慮到在滑動模態運動過程中抖動幅度的控制問題，文獻[4]則從這一角度提出了一種自適應增益切換趨近律：

s(k+1)=μs(k)-ηsgn(s(k))

(17)

并給出了在這一趨近律條件下的抖振幅值：

(18)

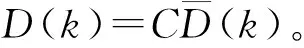
(19)

η(k)=[1+λsgn(s(k))sgn(s(k-1))]η(k-1)

η(0)≥0

其中Dm為擾動的上確界。

該方法的優點是能夠根據系統狀態所處的運動階段來自適應地遞推調整趨近律增益，并且系統的抖振幅值得到了良好的控制。然而單一的趨近律僅僅通過簡單的增益遞推調節難以應對對抗抖動要求較高的場合，通過表達式sgn(s(k))·sgn(s(k-1))來判斷系統的狀態所處的運動階段是一種很經典的方法，然而當系統的狀態處于原點附近并且有著高頻快速的抖動時，該方法就不一定能夠對系統的狀態產生準確的判斷，從而導致錯誤的增益調節，無法快速削弱抖動。

通過對上述兩種方法進行比較，筆者提出一種結合二者優點的新趨近律，具體為：

s(k+1)=μs(k)-tansig(α‖x‖)sgn(s(k))

(20)

將式(20)代入式(10)中，忽略不確定擾動項得到控制律如下：

(21)

此時的實際趨近律為：

s(k+1)=μs(k)-tansig(α‖x‖)sgn(s(k))+D(k)

(22)

由嚴格的不等式達到條件|s(k+1)|<|s(k)|可得系統的收斂條件：

(23)

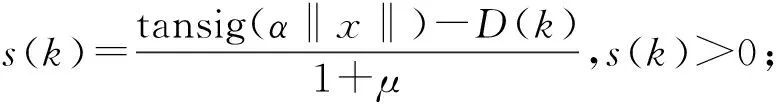
(24)

到達滑動模態面之后有s(k+1)=-s(k)。綜上，系統從任意的初始狀態運動到達準滑動模態面區之后將產生抖振，且振幅為：

(25)

由式(25)可知，振幅與tansig(α‖x‖)和不確定擾動項D(k)的大小有關，和式(17)不同的是，此處是通過調節函數中的參數因子α的值來使得tansig(α‖x‖)逼近擾動項D(k)的值以達到削弱振幅的目的，考慮到準滑動模態面區是在s(k)=0上下鄰近區域，因此將tansig(α‖x‖)在‖x(k)‖=0處進行泰勒展開：

(26)

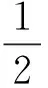
α≤2Dm/‖x‖

(27)

其中D(k)≤Dm，針對式(19)中所述的自適應律的不足，進行如下改進：

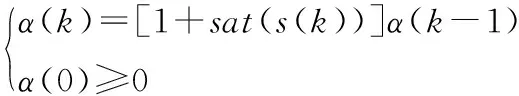
(28)

在上述自適應律的調節下參數α數值變大，s(k)從初始狀態以大步距接近準滑動模態面，由s(k+1)=-s(k)可知進入準滑動模態區的狀態s(k)一直處于穿越原點的抖振狀態中，從穩、準、快的角度來看，控制的關鍵是縮短抖振的時間、控制幅值達到原點的精度和有效地控制抖振的振幅，雙曲正切函數的特性保證了收斂的速度和抖振幅值的衰減控制，而α在自適應律的調節下數值減小，保證了收斂于原點的精度[9,10]。

4 系統的魯棒穩定性

定理1 采用式(28)所示的自適應切換增益，在式(21)變結構控制律的作用下，具有擾動上確界的離散系統式(10)具有魯棒穩定性。

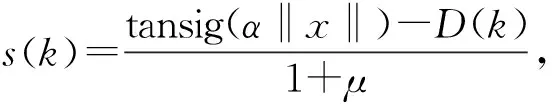
5 系統的MATLAB仿真

系統式(6)中各參數的取值：Kq=3.17m2/s，Kc=1.38×10-12m5/(N·s)，Ap=0.0616m2，Cip=4×10-12m5/(N·s)，Vt=1.96×10-2m3，βe=1×109Pa，Kce=Kc+Ctp=5.38×10-12m2/s，mt=1×105kg，步進梁所輸送的鋼坯屬于慣性負載，故令K=0N/m，且忽略系統的粘滯阻力，則有Bp=0N·s/m。令采樣時間T=0.001s，將以上參數代入式(10)中，可得：

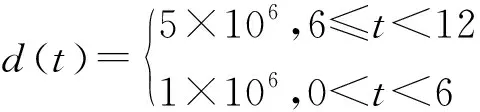
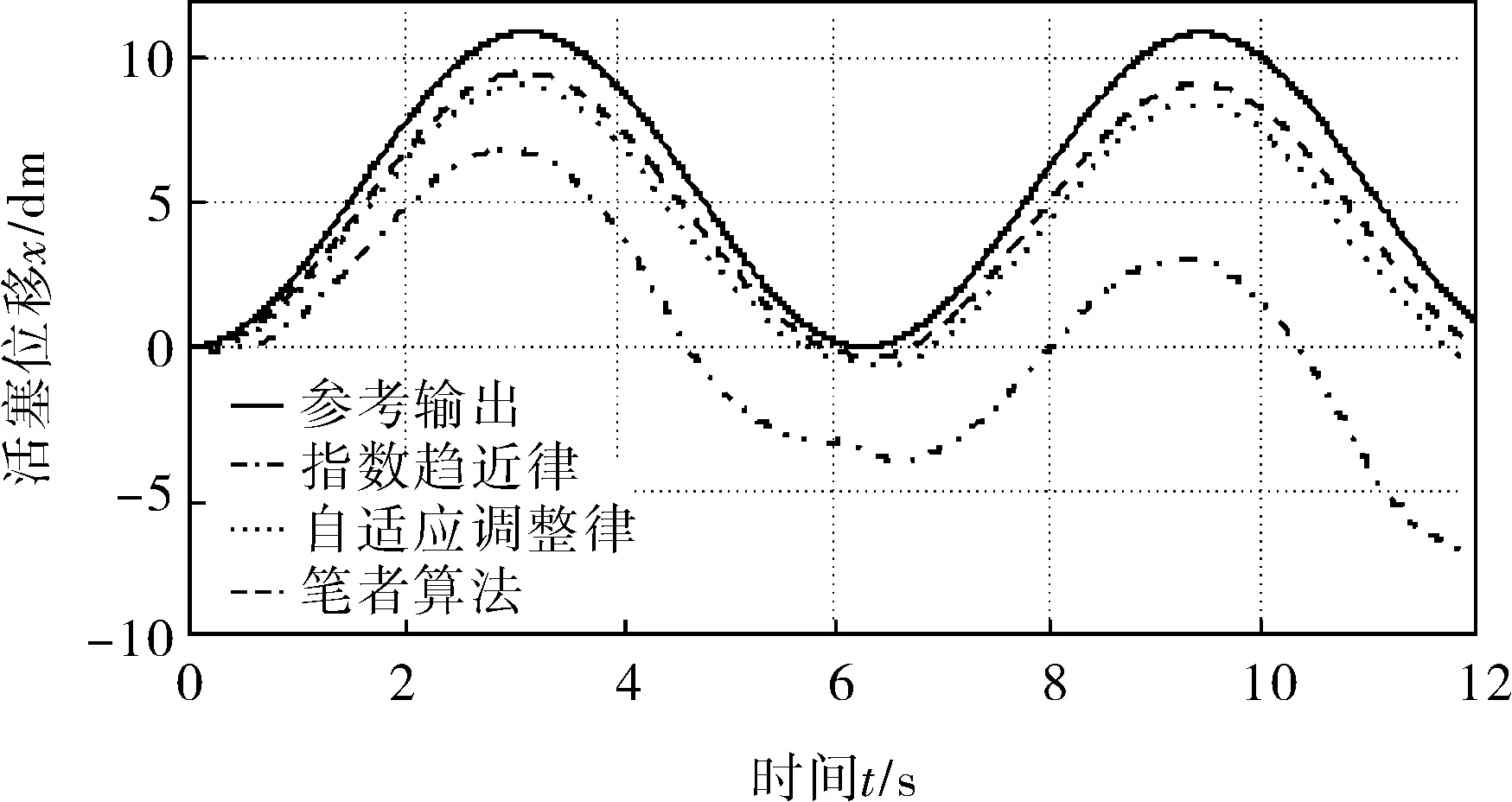
圖3 3種趨近律控制下的活塞位移輸出

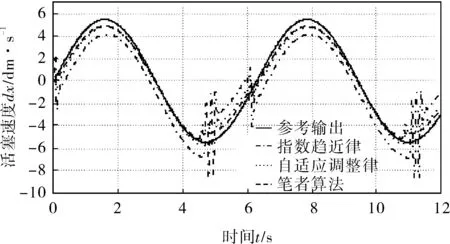
圖4 3種趨近律控制下的活塞速度輸出

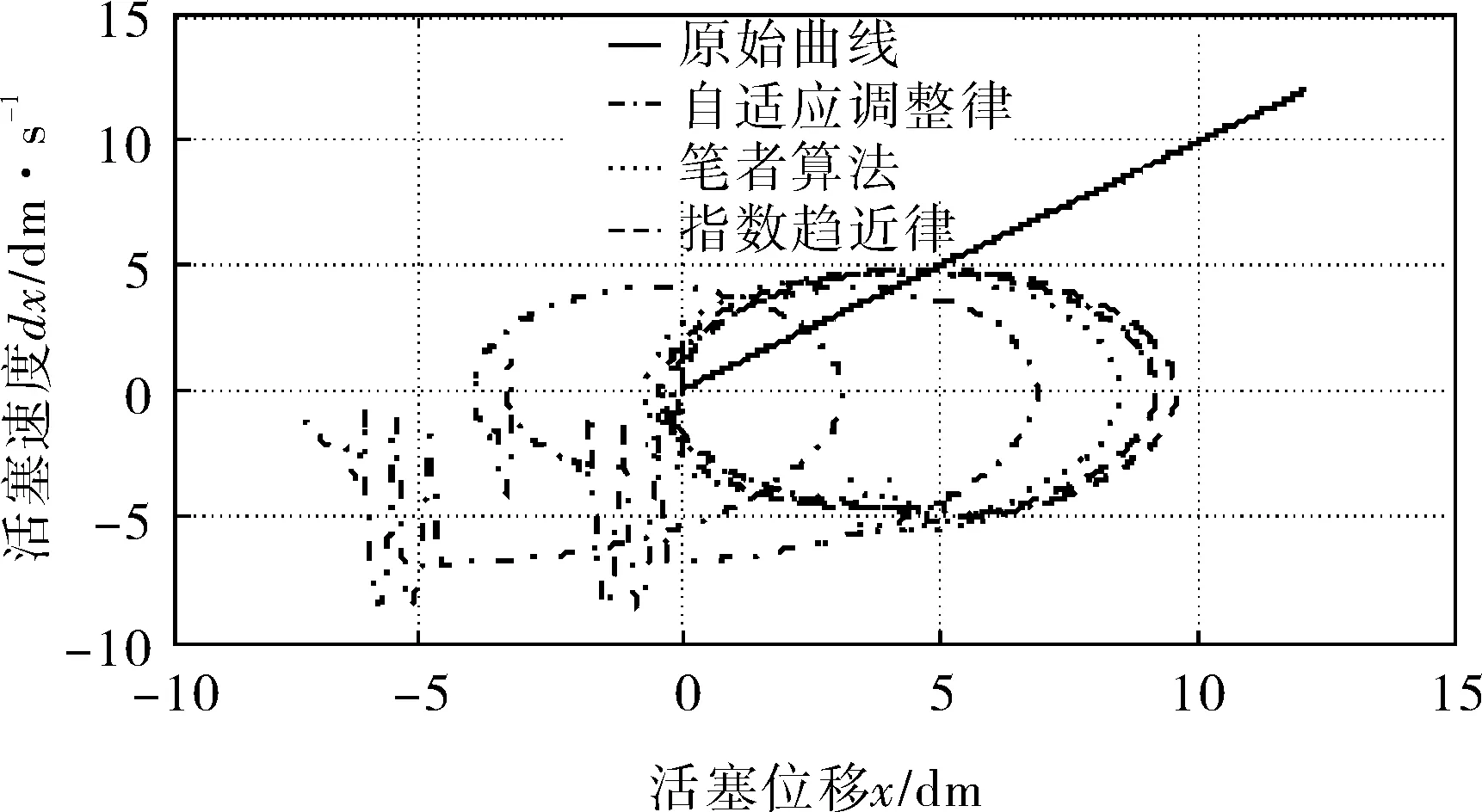
圖5 3種趨近律控制下的系統相平面輸出

由圖3可知在指數趨近律控制下的系統魯棒性較差，無法在大慣性負載擾動下保持良好的位移跟蹤，最高處誤差可達7dm，無法滿足正常的工業生產要求，雖然采用式(17)中的增益自適應控制下系統的跟蹤誤差有所減小，但是在6s處由于擾動的階躍變化產生的脈沖干擾信號對其輸出波形產生了一定的振蕩，在實際輸送鋼坯的過程中會嚴重磨損鋼坯和步進梁的接觸面，縮短步進梁的使用壽命。圖4在指數趨近律和增益自適應趨近律控制下的輸出表明兩者的速度在干擾作用下都產生了局部振蕩，在步進梁上升至等高線和在速度的峰值處尤為明顯，最高振幅分別達到6dm/s和2dm/s，而新的自適應趨近律只有0.5dm/s。圖5表明在正弦信號的輸入作用下，三者最終都處于以原點為奇點的無阻尼運動中。圖3、4中指數趨近律由于常值切換在第一周期產生明顯振蕩。

6 結束語

仿真結果表明筆者提出的新的離散自適應變結構控制策略較好地解決了魯棒性與消抖之間的矛盾。系統趨近運動通過α的正向遞推保證了變結構控制中的大增益切換，使系統獲得強魯棒性，在滑動模態階段，通過α的負向遞推，削弱了滑動模態區的振幅，達到了消抖的目的，結合tansig(α‖x‖)函數的連續切換效果，綜合改善了非線性系統的穩態與動態性能，該算法簡單、有效且易實現，在實際中具有較高的應用價值。