基于小波包與PCA遺傳神經網絡相結合的齒輪箱故障診斷方法

羅 毅 甄立敬

(華北電力大學控制與計算機工程學院，北京 102206)

齒輪箱是風電機組的關鍵部件，也是機組中故障發生率最高的部件，故障百分比已超過60%[1]，齒輪箱一旦發生問題維修非常不便。因此，加強對風電機組齒輪箱的監測和故障診斷，對降低風電場維護費用和提高風電場運行的經濟效益具有重要意義。

齒輪箱故障診斷已成為目前國內外熱門的研究課題之一。郭艷平等通過小波分析等方法診斷了其故障類型和部位，但是小波分析只是對低中頻段部分做了分解，而機組的故障特征信號也存在于高頻信號中[2]。小波包分解能夠較好地提取出振動信號在各個頻帶上的特征信息，并通過這些頻帶上的信息表征齒輪的運行狀態[3]。筆者采用小波包提取時頻域特征值。宋崇智等建立了基于改進Elman神經網絡的齒輪箱故障診斷模型，雖然該方法具有收斂快且能避免局部最小的優點，但是只提取頻域特征值作為神經網絡的輸入[4]。筆者充分考慮故障與時域和時頻域特征值之間的因果關系，選擇提取時域和時頻域特征值。龍泉等提出了一種基于粒子群優化BP神經網絡風電機組齒輪箱故障診斷方法，有一定的實用性，但是選擇的輸入之間具有一定的相關性[5]。主成分分析法可以用較少的互不相關的綜合變量來反映原變量所提供的絕大部分信息，筆者利用主成分分析法消除相關性，確定主成分，從而減少神經網絡的輸入變量[6]。張新海和雷勇介紹了BP神經網絡在機械故障診斷中的應用及實例[7]。BP神經網絡具有較強的非線性擬合能力，遺傳算法是一種高效、并行且全局搜索的方法[8]。

筆者利用遺傳算法與神經網絡結合能有效地解決傳統BP網絡的收斂速度慢、易陷入局部極小值的缺陷，并提高網絡的學習精度[9，10]。提出了一種小波包和PCA遺傳神經網絡相結合的風電機組齒輪箱故障診斷方法。該方法選取振動信號的峭度和峰值作為時域特征值，利用小波包算法提取頻帶能量和二范數作為時頻域特征值。利用主成分分析法消除特征值之間的相關性，得到的新變量作為神經網絡的輸入。利用遺傳算法對BP神經網絡權值和偏置進行優化，建立遺傳神經網絡對故障進行診斷。

1 小波包與PCA遺傳神經網絡結合算法①

1.1 小波包分解

小波包算法是一般化的小波變換，對信號的低、高頻都需要進行分解，彌補了小波分析的不足[11]，齒輪箱發生故障時不同故障類型的振動信號在相同頻帶內信號的能量和二范數會發生變化，它使得一些頻帶內的信號能量有增大或減小的趨勢，因此，在各頻帶成分信號的能量和二范數中包含著豐富的故障信息。所以筆者選用利用頻帶能量和二范數來構造振動信號的特征向量，其構造過程如下：

a. 利用db小波對采集來的信號S(t)進行三層小波包分解，從而獲得從低頻到高頻的8個小波包分解系數。

b. 對小波包分解系數進行單節點重構，提取8個頻帶范圍的重構信號S3j(j=0，1，…，7)，它分別包含了故障信號從低頻到高頻的信息。

d. 特征向量的構造。齒輪箱發生故障會直接導致振動信號時域特征參數的變化。為了有效反映齒輪箱的運行狀態，通常組合選用若干個時域特征參數進行故障診斷，筆者采用峭度xkur和峰值xp兩個時域特征參數作為振動信號的特征量[12～14]。構造振動信號的一個18維特征向量x=[xp，xkur，E0，E1，E2，E3，E4，E5，E6，E7，A0，A1，A2，A3，A4，A5，A6，A7]，從而得到故障特征特征樣本矩陣。

1.2 主成分分析

筆者構造的振動信號特征向量與齒輪箱故障有較確定的因果關系，為消除特征向量x元素間的相關性，利用主成分分析法，降低特征向量x的維數，用較少的互不相關的綜合變量反映原變量所提供的絕大部分信息，通過對新變量的分析達到解決問題的目的，從而減少神經網絡的輸入變量[15]。設有n組數據，特征向量R的維數為p，即每組數據包含p個變量，得到故障特征樣本矩陣Xn×p，主成分分析法簡化輸入的過程如下[16，17]：

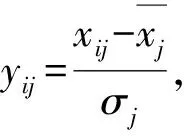
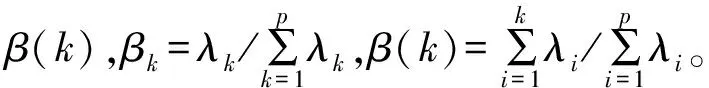
d. 求出主成分Z=Yα，若?α∈(0,1)，且當β(s)≥α，則Z1,Z2，…，Zs稱為樣本X1,X2,…,Xp的顯著性水平為α的主成分。其中β(s)為第s個主成分累計貢獻率。以Z1,Z2,…,Zs來代替X1,X2,…,Xp，既降低了輸入維數又消除了原樣本空間的自相關性。

1.3 遺傳神經網絡建模

筆者采用遺傳算法優化神經網絡的初始權值和閾值，分兩步進行：首先利用遺傳算法群體尋優策略，采用遺傳算法對網絡權值和閾值進行全局搜索，保證其落入全局最優點的領域；然后用L-M法對網絡權值和閾值進行細化訓練以進一步減小誤差，使其收斂于全局最優解或性能更好的近似最優解。該網絡能夠充分發揮遺傳算法的全局收斂和L-M算法的指導性搜索思想。

筆者選用的BP網絡采用三層神經元結構，即一個輸入層、一個隱含層和一個輸出層。輸入層神經元為Z1,Z2,…,Z12；輸出層為齒輪箱12個部件的狀態T1,T2,…,T12，正常為0，故障為1，根據遺傳神經網絡的輸出就可以診斷出故障類型。遺傳神經網絡結構如圖1所示。

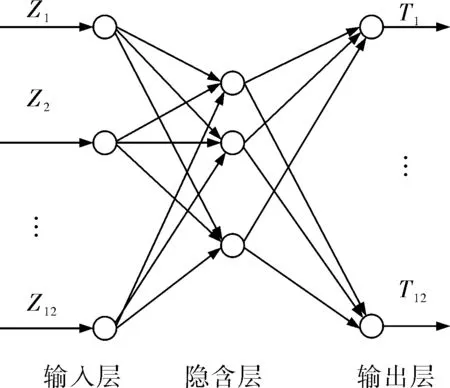
圖1 遺傳神經網絡結構

筆者提出的小波包和PCA遺傳神經網絡相結合算法，先利用小波包分解得到故障特征樣本矩陣Xn×p，然后利用主成分分析得到新變量矩陣Zn×s，最后利用遺傳神經網絡得到輸出向量T，根據向量T即可得到齒輪箱的故障類型。小波包與PCA遺傳神經網絡結合算法的流程如圖2所示。

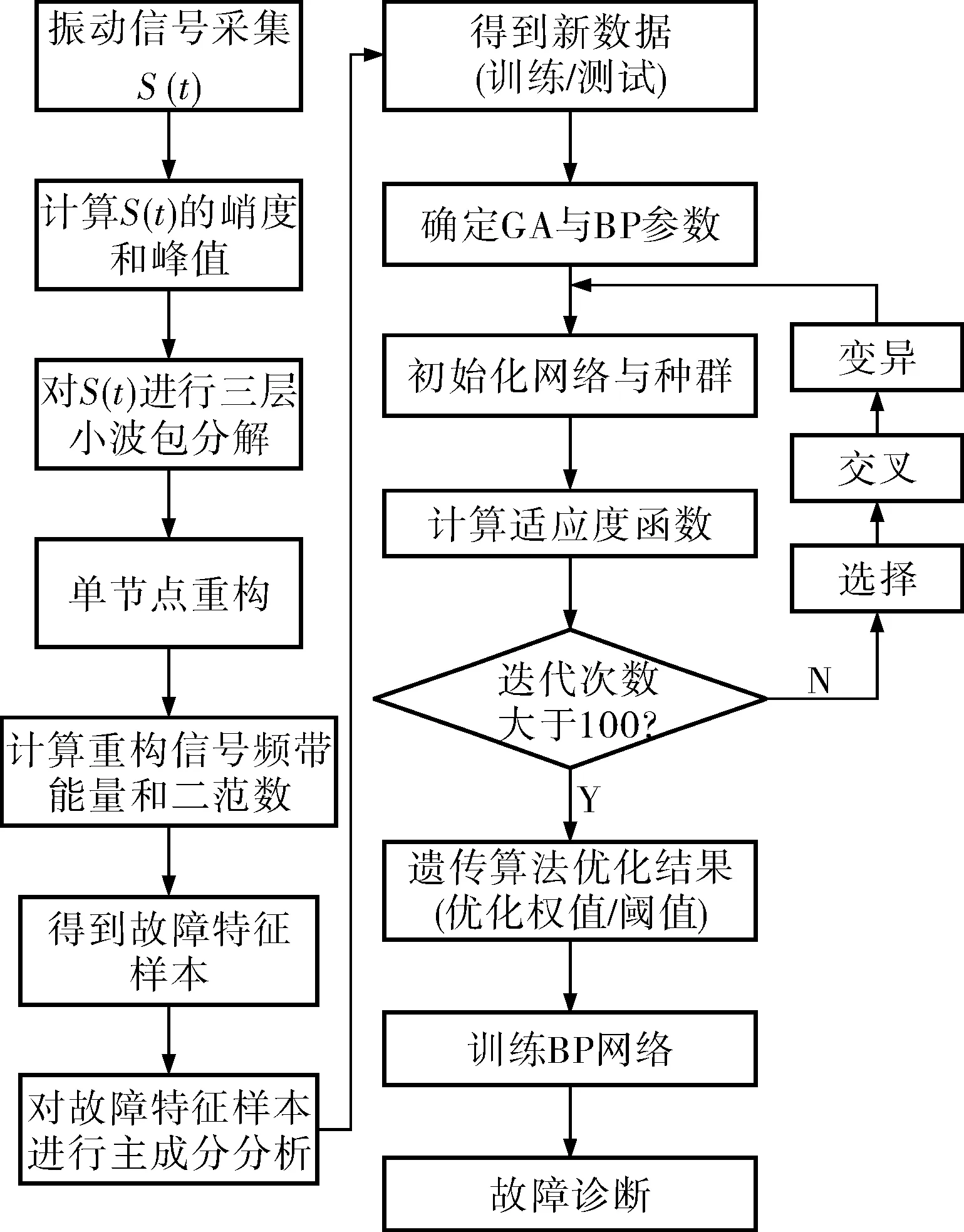
圖2 小波包與PCA遺傳神經網絡結合算法的流程

2 仿真測試

2.1 實驗系統簡介

風電機組齒輪箱的主要結構包括軸、齒輪和軸承。故障從結構上可以分為：軸的故障(軸不對中、軸不平衡及軸彎曲等)、軸承故障(軸承內/外圈磨損及滾動體磨損等)和齒輪故障(齒面剝落、齒面膠合、齒面磨損及斷齒等)。筆者選用的被測設備為某風電場的風電機組齒輪箱，被測設備為工業通用齒輪箱，齒輪箱結構如圖3所示。

圖3 風電機組齒輪箱結構

在齒輪箱前、后端軸承上安裝加速度傳感器，齒輪箱輸入軸安裝轉速故障實驗在某公司的機械故障綜合模擬實驗臺上進行，通過換軸承、齒輪或軸可以改變故障類型，這樣可以達到模擬齒輪箱故障的目的，從而得到不同故障類型時的振動信號。采集齒輪箱的加速度振動信號，采樣頻率為66.7kHz。筆者選取齒輪箱7種故障類型(表1)進行分析，每種故障選取40組樣本作為訓練數據，3組樣本作為測試數據，以此作為原始數據樣本。表1中IS為輸入軸、OS為輸出軸、ID為從動軸、IS為輸入側、OS為輸出側。

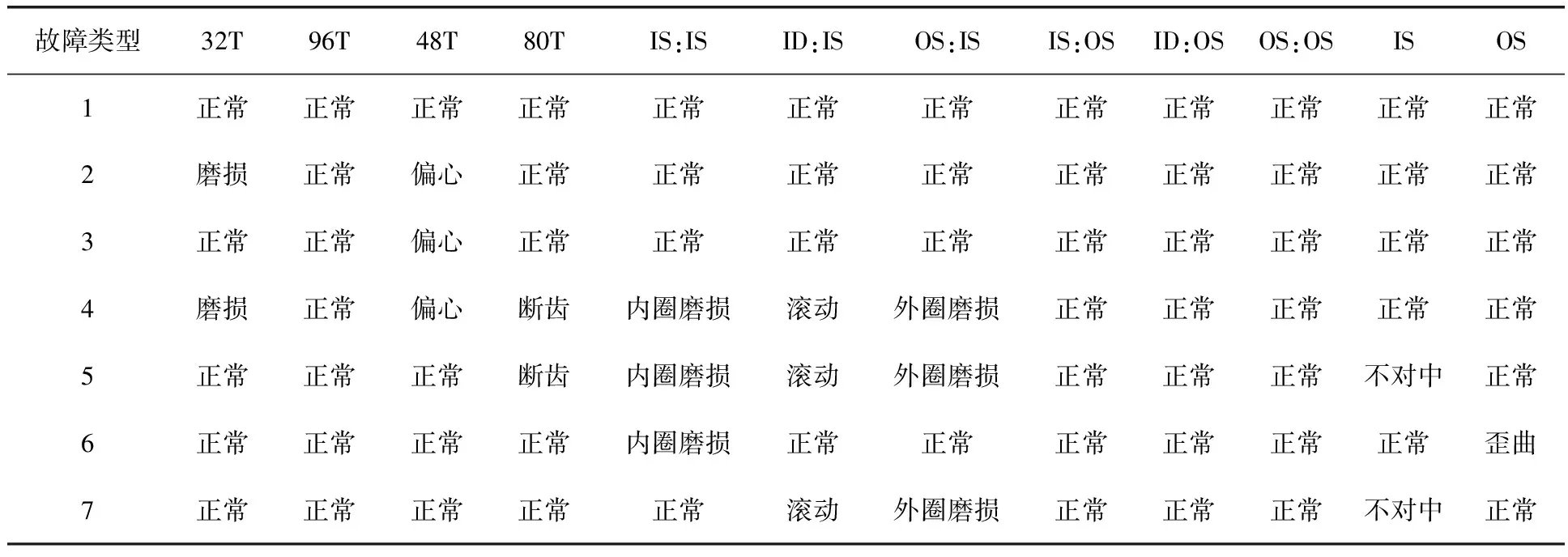
表1 齒輪箱故障類型

2.2 利用小波包和主成分分析處理數據

筆者對7種故障類型的振動信號進行分析，利用三層小波包變換提取頻帶能量和二范數作為時頻域特征值，提取峰值和峭度作為時域特征值，構造振動信號的一個18維特征向量，每種故障振動信號下的特征樣本各43組，故得到故障特征矩陣X301×18，X301×18的部分數據列于表2。

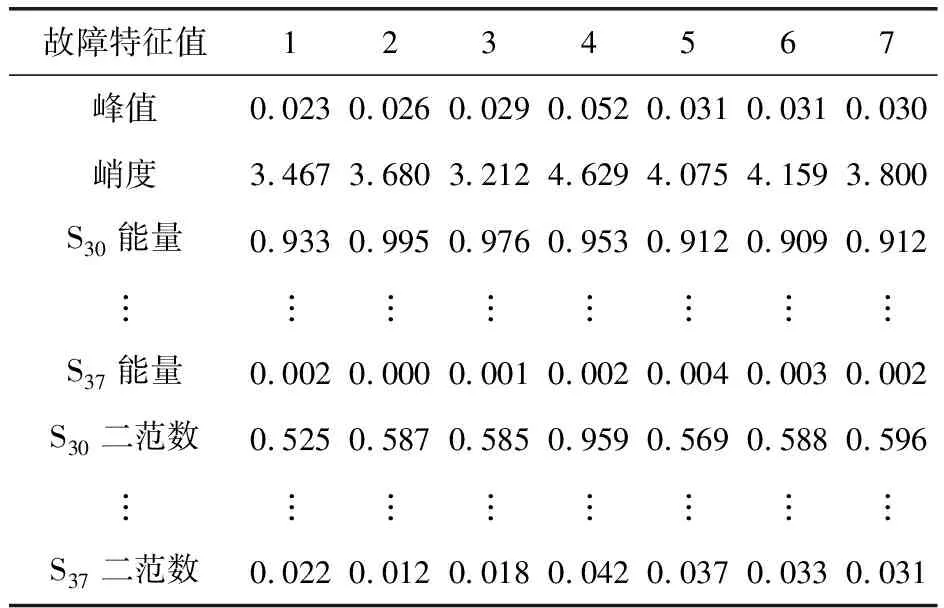
表2 風電機組齒輪箱故障特征值樣本

為消除故障特征樣本X301×18各變量單位和數量級不同的影響，先對X301×18進行標準化理，得到新的數據矩陣Y301×18，然后對矩陣Y301×18進行主成分分析，可得到新變量協方差矩陣特征值表(表3)。取α=95%，由表3可知β(4)≥α，則以Z1，Z2，Z3，Z4來代替X1，X2，…,X18，得到4個新的綜合指標變量，這樣既降低了輸入維數又消除了特征值間的相關性。

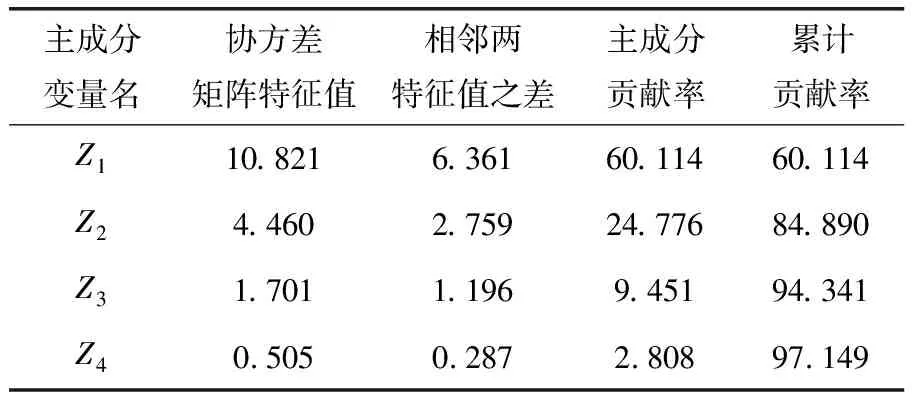
表3 新變量的協方差矩陣特征值

2.3 利用遺傳神經網絡進行故障診斷

BP神經網絡的輸入為經主成分分析后確定的新變量，輸入層神經元個數為4，輸出為齒輪箱12個部件的狀態，輸出層神經元個數為12；將隱含層神經元個數設為輸入層神經元個數的兩倍再加一[18]。學習速率為0.01，訓練目標為0.01。遺傳算法在進化搜索過程中是以適應度函數為依據的，筆者選取誤差平方和的倒數作為適應度函數；權重個體的基因位數較長，所以采用浮點數編碼；初始種群大小為100；選擇輪盤賭抽樣；算術交叉概率為0.90；非統一變異概率為0.09；最大進化代數為100代。每種故障類型各選取40組樣本作為訓練樣本，用280組樣本對網絡進行訓練。

主成分分析后所得數據作為神經網絡的輸入，利用遺傳算法優化神經網絡的初始權值和閾值，經過100代繁殖后，退出遺傳算法，得到神經網絡權值和閾值的初始值，優化過程如圖4所示。

圖4 適應度函數進化曲線

從圖4可以看出，遺傳繁殖到72代時，最佳適應度函數已不再發生變化，即說明遺傳算法已對神經網絡的權值和閾值進行了全局搜索，找到粗略的最優值區域。找到粗略的最優值區域之后，為進一步減小誤差，對神經網絡采用L-M算法進行細化訓練。完成網絡的建立和訓練后，每種故障類型各選取3組樣本對網絡進行測試，部分輸出的故障診斷結果見表4。

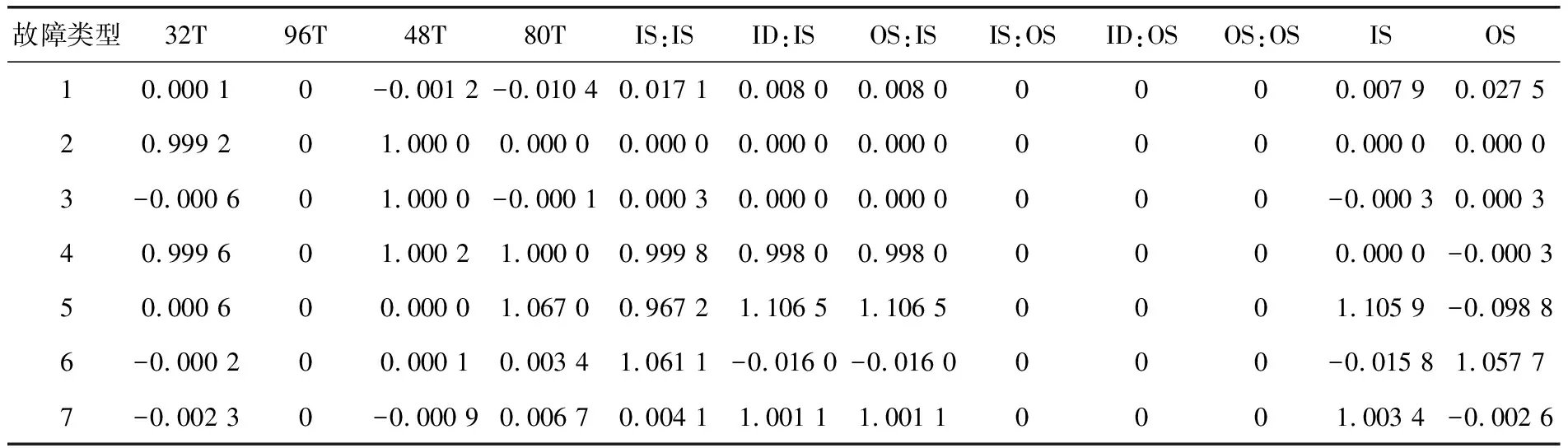
表4 狀態識別結果

從表4的數據可判斷出第一組數據為正常狀態，第二組數據為32T磨損、48T偏心，第三組數據為48T偏心，第四組數據為32T磨損、48T偏心、80T斷齒、輸入軸承內圈磨損、從動軸承滾動、輸出軸承外圈磨損，第五組數據為80T斷齒、輸入軸承內圈磨損、從動軸承滾動、輸出軸承外圈磨損、輸入軸不對中，第六組數據為輸入軸承內圈磨損、輸出軸歪曲，第七組數據為從動軸承滾動、輸出軸承外圈磨損、輸入軸不對中。

2.4 結果分析

為了進一步說明小波包與PCA遺傳神經網絡相結合算法的有效性，實驗比較了不同算法下的平均故障識別率，分類器均采用BP神經網絡，實驗結果見表5。由表5可知，筆者所采用的小波包與PCA遺傳神經網絡相結合算法對風電機組齒輪箱故障診斷的結果準確、精度高。

表5 故障識別率 %

注：TFD為時頻域特征值，即提取的小波包頻帶能量和二范數；TD為時域特征值，即提取的峭度和峰值。

3 結束語

筆者提出的小波包與PCA遺傳神經網絡相結合算法診斷結果準確，精度高。該方法選取振動信號的峭度和峰值作為時域特征值，利用小波包算法提取頻帶能量和二范數作為時頻域特征值。利用主成分分析法消除18個特征值之間的相關性，確定主成分，作為遺傳算法優化的BP神經網絡的輸入，進行故障診斷。仿真測試表明了算法的有效性。