脈沖微分系統的等度積分φ0－穩定

王培光，劉曉靜

（1.河北大學 電子信息工程學院，河北 保定 071002；2.河北大學 數學與計算機學院，河北 保定 071002）

本文利用錐值Lyapunov函數和比較方法討論了如下脈沖微分系統零解的積分φ0 －穩定性：

和它的擾動系統

其中f，h∈PC［R＋×S（ρ），Rn］，Ik，Mk∈C［S（ρ），Rn］，f（t，0）＝h（t，0）＝Ik（t，0）＝Mk（t，0）≡0，0≤t0＜t1＜t2＜…＜tk…，limk→∞tk＝∞，k＝1，2，….

近年來積分穩定性理論得到了快速發展［1－6］，但是，到目前為止關于積分φ0 －穩定性的研究并不多見［7－9］.本文主要討論了脈沖微分系統零解的等度積分φ0 －穩定性.

1 預備知識

定義1 Rn中的子集K 稱為錐，如果滿足如下條件：（i）λK?K，λ≥0；（ii）K＋K?K；（iii）K＝（iv）K0≠Φ；（v）K∩（－K）＝0，其中，K0及?K 分別表示K 的閉包，內部和邊界.

定義2 稱集合K＊＝｛φ0：φ0∈Rn，對任意x∈K，（φ0，x）≥0｝為K 的伴隨錐，如果K＊滿足定義1中條件（i）－（v）.

通過以上定義可得x∈?K 當且僅當存在φ∈K＊0，K0＝K－｛0｝，（φ，x）＝0.

為方便起見，給出如下函數類：

S（ρ）＝｛x∈K：‖x‖＜ρ，ρ＞0｝.

K＝｛b∈C［［0，ρ），R＋］，b（0）＝0，且b（r）關于r是嚴格遞增的｝.

PC＝｛f：R＋×S（ρ）→Rn在區間（tk，tk＋1］×Rn上連續，且極限存在｝.

下面利用比較方法研究脈沖微分系統零解的等度積分φ0 －穩定性準則.為此，考慮如下比較脈沖微分方程

和它的擾動微分方程

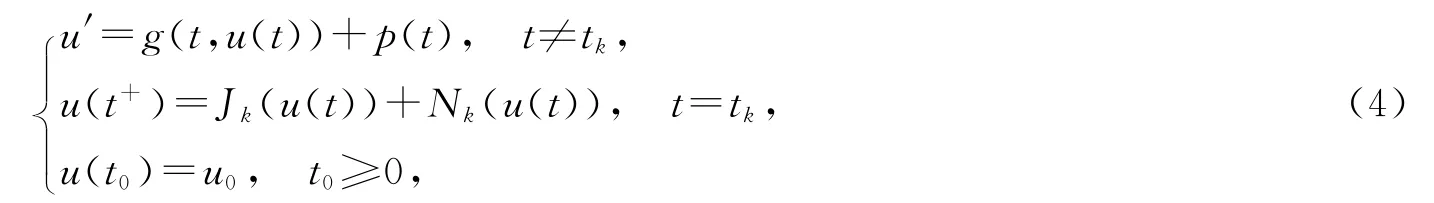
其中g∈PC［R＋×R＋，R＋］，p（t）∈PC［R＋，R＋］，Jk，Nk∈C［R＋，R＋］，R＋＝［0，＋∞），g（t，0）＝Jk（t，0）≡0，0≤t0＜t1＜t2＜…＜tk…，limk→∞tk＝∞，k＝1，2，….

下面給出函數類V0的定義：

V0＝｛V（t，x）∈PC［R＋×S（ρ），K］：V 在（tk，tk＋1］×S（ρ）上連續2，…，V（t，x）對任意的t關于x 滿足局部Lipshitzian條件｝.

定義3 設V∈V0，定義

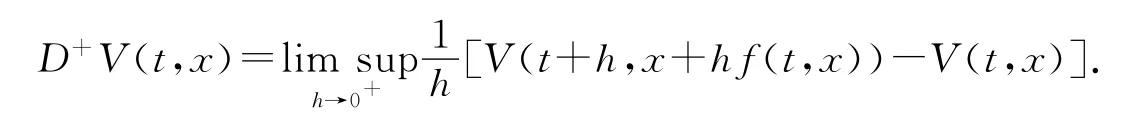
定義4 稱系統（1）的零解

（IS1）是等度積分φ0 －穩定的，如果對任意α≥0，t0∈R＋，存在函數β（t0，α）≥0，其中β在t0上是連續的，α，β∈K，使得當φ0∈，（φ0，x0）≤α，T＞0.

有（φ0，x＊（t））＜β，其中x＊（t）＝x＊（t，t0，x0）是系統（2）的右行最大解.

（IS2）是一致積分φ0 －穩定的，如果（IS1）中的α，β都與t0無關.

（IS3）是φ0 －吸引的，如果對任意的ε＞0，α≥0，t0∈R＋，存在函數β（t0，α）≥0，其中β在t0上是連續的，T＝T（t0，α，ε），γ＝γ（t0，α，ε），使得當φ0∈K＊0，（φ0，x0）≤α，T＞0，

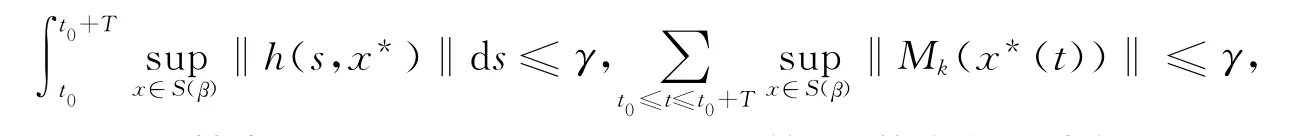
有（φ0，x＊（t））＜ε，t≥t0＋T，其中x＊（t）＝x＊（t，t0，x0）是系統（2）的右行最大解.

（IS4）是一致φ0 －吸引的，如果（IS3）中的T，γ都與t0無關.

（IS5）是等度漸近積分φ0 －穩定的，如果（IS1），（IS3）都成立.

（IS6）一致漸近等度積分φ0 －穩定的，如果（IS2），（IS4）都成立.

注1 稱系統（3）的零解是等度積分穩定的，如果對任意α≥0，t0∈R＋，存在t0上連續的函數β（t0，α）≥0，α，β∈K，使得當‖x0‖≤α，T＞0，

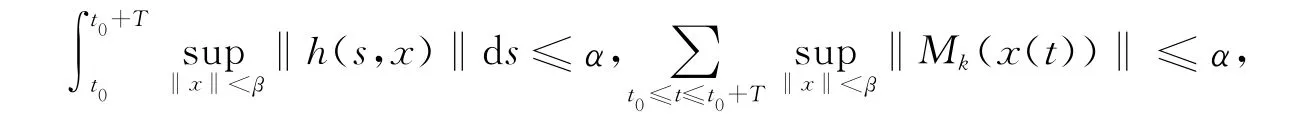
有‖x（t）‖＜β，t≥t0，其中x（t）＝x（t，t0，x0）是系統（4）的解.其他積分穩定定義可以類似給出，不再贅述.

為得到主要結果，可有如下引理.

引理1 令φ0∈，V∈V0，g∈PC（R＋×R＋，R＋），Jk（x）是單調非減的，若下列條件成立：

（L1）D＋（φ0，V（t，x））≤g（t，（φ0，V（t，x）））， t≠tk，

（L2）（φ0，V（t＋，x＋Ik（x）））≤Jk（φ0，V（t，x））， t＝tk，

（L3）（φ0，V（t0，x0））≤u0， k＝1，2…，

則（φ0，V（t，x（t）））≤u＊（t），t≥t0，其中u＊是系統（4）的右行最大解.

證明：令m（t）＝（φ0，V（t，x）），因為m（t0）≤u0，通過第二比較定理［10］，有

又由Jk（x）單調非減及引理1（L2），條件（5）得

可得m（t）≤u＊（t），t0≤t≤t2.

由數學歸納法知

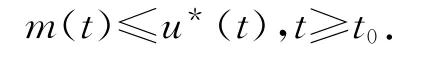
2 主要結果

定理1 假設V（t，x）∈V0，引理1的所有條件都成立并且滿足下列條件：

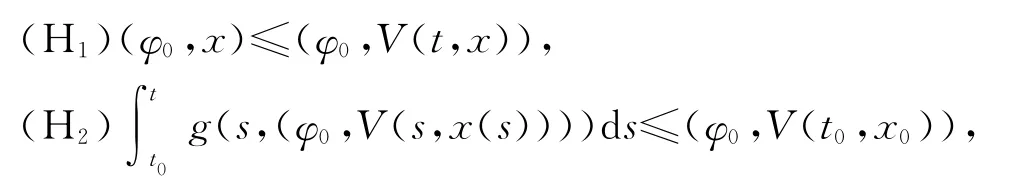
則系統（3）零解的等度積分穩定蘊含系統（1）零解的等度積分φ0 －穩定.

證明：因為系統（3）的零解是等度積分穩定的，則對α≥0，t0∈R＋，存在β（t0，α）≥0，α，β∈K，使得當T＞0，

其中u＊（t）＝u＊（t，t0，u0）是系統（4）的右行最大解.

令‖h（t，x＊）‖＝M1p（t），‖Mk（x＊）‖＝M2Nk（u），其中M1，M2＞0為常數，u0＝（φ0，V（t0，x0）），φ0∈，因此

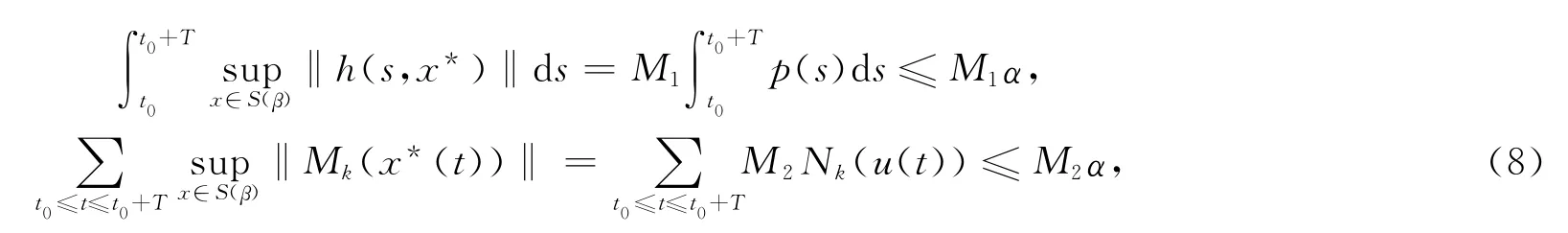
其中x＊（t）＝x＊（t，t0，x0）為系統（2）的右行最大解.

由引理1知

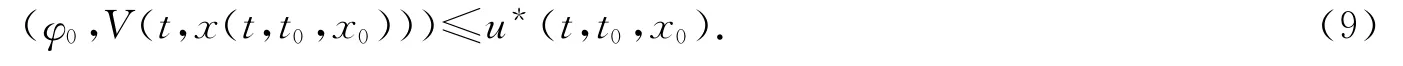
由引理1的條件（L1）和定理1的條件（H2）可得

對φ0∈，由式（9），（10）得

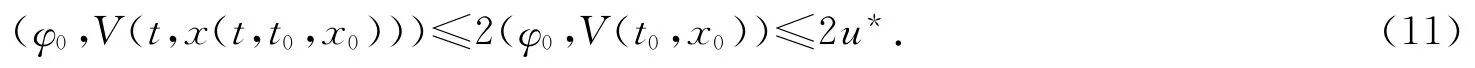
因此通過條件（H1）和不等式（7），（11）得

令α＊＝min｛α，M1α，M2α｝，當T＞0，

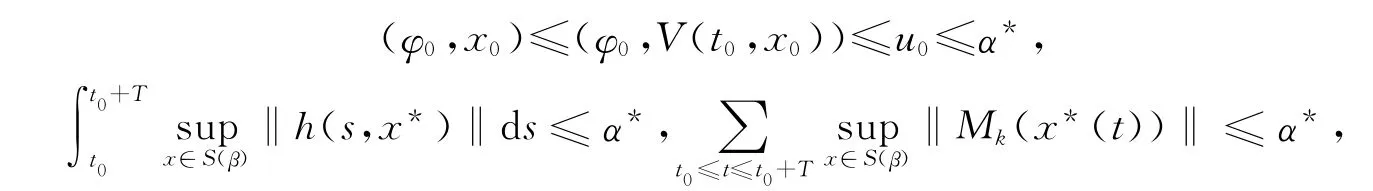
有（φ0，x＊）＜β＊.因此系統（1）的零解是等度積分φ0 －穩定的.

定理2 假設V（t，x）∈V0，引理1的所有條件都成立，定理1的條件（H2）成立，φ0∈K＊0，（t，x）∈R＋×S（ρ），且還滿足下列條件：

（H3）a（（φ0，x））≤（φ0，V（t，x）），a－1（q）＝q，a∈K，

（H4）b（‖x‖）≤（φ0，V（t，x）），b∈K，

則系統（3）零解的等度漸近積分穩定蘊含系統（1）零解的等度漸近積分φ0 －穩定.

證明：因為（H3）蘊含（H1），系統（3）的零解是等度漸近積分穩定的，首先，由定理1知系統（1）的零解是積分φ0 －穩定的.其次，系統（3）的零解是吸引的，對ε＞0，t0∈R＋，存在

α＝α（t0）＞0，T＝T（t0，ε）＞0，γ＝γ（t0，α，ε），

使得當u0≤α，

其中u＊（t）＝u＊（t，t0，u0）是系統（4）的右行最大解.

當（φ0，V（t0，x0））≤u0時，有‖x‖→0（t→∞）.

假設上式不成立，則存在一個序列｛t（n）｝，t（n）≥t0＋T，使得當t（n）→0（t→∞）時，有

由引理1得

由（H4），式（12），（13），（14）得

b（ε）≤b（‖x（t（n））‖）≤（φ0，V（t（n），x（t（n），t0，x0））≤u＊（t（n），t0，u0）＜b（ε），

產生矛盾，因此‖x‖→0（t→∞），從而有（φ0，x）→0（t→∞）.

令‖h（t，x＊）‖＝N1p（t），‖Mk（x＊）‖＝N2Nk（u），其中N1，N2＞0為常數，因此

其中x＊（t）＝x＊（t，t0，x0）是系統（2）的右行最大解.

令γ＊＝min｛N1γ，N2γ｝，當T＞0，

時，有（φ0，x＊）＜ε.因此系統（1）的零解是等度漸近積分φ0 －穩定的.

［1］ LAKSHMIKANTHAM V，LEELA S.Differential and integral inequalities［M］.New York：New York Academic Press，1969.

［2］ HRISTOVA S G.Integral stability in terms of two measures for impulsive functional differential equations［J］.Math Comput Modelling，2010，51：100－108.

［3］ HRISTOVA S G.Integral stability in terms of two measures for impulsive differential equations with“supremum”［J］.Comm Appl Nonlinear Anal，2009，16（3）：37－49.

［4］ 郭飛.脈沖混合微分系統關于兩側度的穩定性分析［D］.濟南：山東師范大學，2003.GUO Fei.Stability analysis for impulsive differential hybrid systems in terms of two mesaures［D］.Ji'nan：Shandong Normal University，2003.

［5］ VRKOC I.Integral stability［J］.Czechoslovak Math，1959，09（1）：71－129.

［6］ MARTYNYUK A A.On integral stability and Lipschitz stability of motion［J］.Ukrainian Math J，1997，49（1）：84－92.

［7］ HRISTOVA S G，RUSSINOV I K.φ0－Integral stability in terms of two measures for differential equations［J］.Math Balkanica，2009，23（1－2）：133－144.

［8］ 樊永艷，張靜.脈沖交混合系統的積分φ0－穩定［J］.滄州師范學院學報，2013，29（2）：2095－2910.

［9］ SOLIMAN A A，ABDALLA M H.Integral stability criteria of nonlinear differential systems［J］.Math Comput Modelling，2008，48：258－267.

［10］ 尤秉禮.常微分方程補充教程［M］.北京：人民教育出版社，1981.