基于多新息理論的PID神經網絡改進算法

孫敏敏 秦品樂

（中北大學計算機與控制工程學院 山西 030051）

0 引言

文[1]將PID控制與神經網絡結合，提出了PID神經網絡，PID神經網絡具有PID控制規律，與傳統的前向神經網絡相比具有神經元的輸入輸出呈現出動態性，原因在于往神經網絡中引入了比例（P）、積分（I）、微分（D）神經元。PID神經網絡同時具備傳統前向神經網絡逼近任意非線性函數的特性，能夠進行非線性，動態復雜系統的辨識與控制。文[2]采用BP算法的批處理模式進行神經元網絡權值的調整，不便于系統實時辨識和控制，受文[3]的啟發，采用BP算法的在線模式進行權重值的修正進行系統辨識，這為本文將多新息辨識算法引入PID神經網絡做了準備。PID神經網絡采用傳統的BP算法的批處理模式進行權值的修正，從辨識的精度上考慮，批處理法擬合系統實際輸入輸出的效果優于在線模式，但從實時辨識與控制角度考慮，在線模式優于批處理法。在線模式對權值的修正值利用了系統當前的輸入輸出數據，沒有利用歷史的輸入輸出數據，壞數據對網絡權值修正的影響大。丁鋒等人提出的多新息辨識方法利用當前與歷史輸入輸出數據，能減小壞數據的影響，提高系統辨識的精度。受文[4]啟發，本文將多新息辨識方法引入PID神經網絡，提出基于PID神經網絡的多新息學習算法并給出了收斂性證明，仿真實例說明能取得較好的效果。

1 PID神經網絡多新息學習算法

考慮1+?pt到t時刻的p組輸入輸出數據，PID神經網絡輸入層各節點的輸出向量為

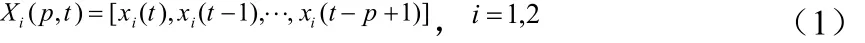
輸出層節點的輸出向量為

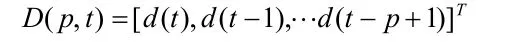
理想輸出向量為

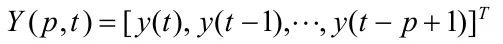
誤差函數變為

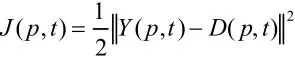
那么，PID神經網絡的隱含層至輸出層權值修改式為

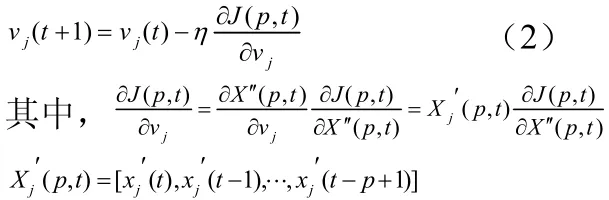
網絡的輸入層至隱含層權值修改式為

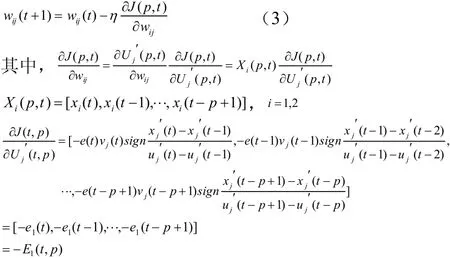
從而有隱含層至輸出層權值修改式為

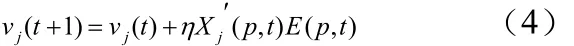
輸出層至隱含層權值調整式為

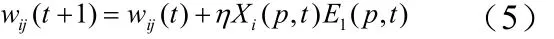
2 仿真實例

為了說明所提出的基于PID神經網絡的多新息學習算法的有效性，在和PID神經網絡采用的標準BP算法進行比較時，采用文獻[7]中的例子。

例1.考慮下面方程描述的非線性動態系統

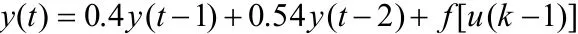
其中)(ty為t時刻系統輸出，)(tu為t時刻系統輸入。

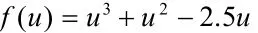
輸入函數為

網絡采用在線梯度法，每個學習回合采集200個樣本點進行學習和訓練，輸入層至隱含層權值矩陣的初始值為W(0)=[1,0.1,1;?1,?0.1,?1]，隱含層至輸出層權值向量的初始值為V(0)=(0.1,0.1,0.1)，其中y(t)為網絡理想輸出，d(t)為網絡實際輸出。取新息長度p=2，學習率η=0.175，當網絡學習和訓練20步后，改進算法與未改進算法的辨識結果如圖1和圖2所示。

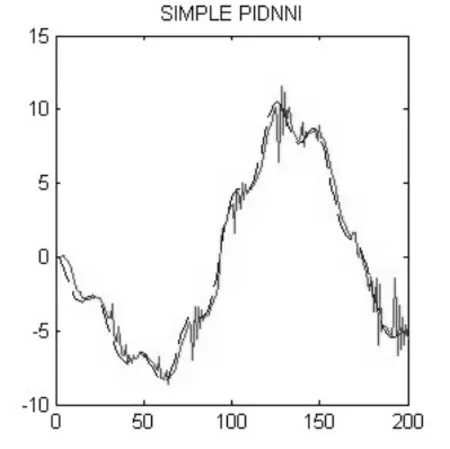
圖1 未改進算法的辨識結果

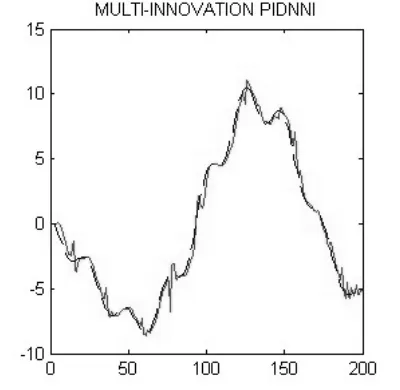
圖2 改進算法的辨識結果

3 結語

結合多新息辨識理論，推導出基于多新息理論的PID神經網絡算法。仿真實例表明所提出的算法能有效估計參數，且具有較快的收斂速度。

[1]舒懷林.PID控制與神經網絡的結合及PID神經網絡非線性控制系統[M].第十九屆中國控制會議論文集（二），2000：228-332

[2]舒懷林.PID神經元網絡及其控制系統[M].北京：國防工業出版社，2006：23-51

[3]許少云.BP學習算法的在線模式與批處理模式[M].1996年中國智能自動化學術會議論文（上冊），1996

[4]劉英玉.一種基于前向神經網絡的多新息隨機梯度算法[J].哈爾濱商業大學學報（自然科學版）2006，22（2）

[5]Feng Ding，Tongwen Chen.Performance analysis of multi-innovation gradient type identification methods.2009，43（1）：1-14

[6]郭雷.時變隨機系統-穩定性、估計與控制.長春：吉林科學技術出版社，1993

[7]舒懷林.PID神經網絡及其非線性動態系統辨識能力分析[J].自動化與信息工程