關于多圓盤 Hardy空間上本性正規的 Beurling型商模的一些探討

莊春明，戴星超

（浙江師范大學 數學系， 浙江 金華 321004）

關于多圓盤 Hardy空間上本性正規的 Beurling型商模的一些探討

莊春明，戴星超

（浙江師范大學 數學系， 浙江 金華 321004）

本文主要討論了多圓盤 Hardy 空間上本性正規的 Beurling 型商模，并得到了 Beurling 型商模本性正規的一個 必要條件.

Hardy 空間；Beurling 型商模；多圓盤

0 引言

設 D={z∈C:|z|<1}是復平面 C中的單位圓盤,Cn是 C上的線性空間,Cn中的單位多圓盤記為 Dn,設 Tn是 Dn的特征邊界,其中 Dn和 Tn分別是 D和 T的 n重 Descartes乘積.記dσ 是 Tn的正規 Haar測度,Lp(Tn)=Lp(Tn,dσ)是 Tn的 Le-besgue可測空間.H2(Dn)表示 L2(Tn)上全體解析多項式的閉包.

Douglas和 Paulsen[1]引入了 Hilbert模的概念,并使用模理論方法研究了算子理論問題.Arveson[2]將本性正規 Hilbert模定義為:如果 Hilbert模 N的自伴交換子都是緊的,那么稱 N是本性正規的.一個自然的問題是,哪些商模是本性正規的?人們發現,大部分單位球上的 Hardy模、Bergman模和 d-位移的 Hilbert模甚至一些子模是本性正規的[1,2].但對于多圓盤情形,這方面結果有很大差異.Douglas和 Misra[3]證明了商模]是本性正規的.Guo和 Wang[4]后來刻畫了雙圓盤本性正規的 Beurling型商模.本文將討論該結果[4]在多圓盤的情形.首先,簡單介紹本文涉及到的基礎知識.

設(Mz1,Mz2,…,Mzn)為 H2(Dn)上的多元坐標算子組,則 H2(Dn)在多項式環 C[z1,z2,…,zn]作用下的一個 Hilbert模.設 η 是一個內函數,M=[η]=ηH2(Dn)是由 η 生成的 Guo和 Wang[4]所謂的 Beurling型子模,而商模稱為 Beurling型商模.設 Pη是到 N的投影,則,則商模N是一個 Hilbert模,模結構為設，對于 i=1,2,…,n,H2(D)在 zi∈D的 正規再生核 為)在 z的正規再生核為

1 主要結果

本節先介紹三圓盤上的自伴交換子在 Beurling型商模N為緊算子的性質,再推廣到多圓盤,最后給出 Beurling型商模本性正規的必要條件.對于 1≤k≤n,記

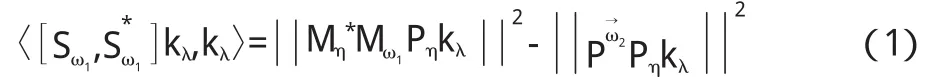
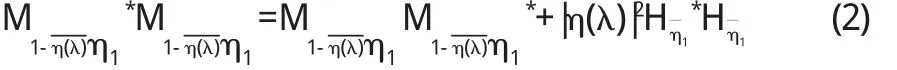
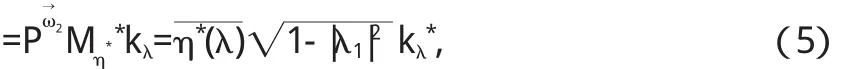
于是

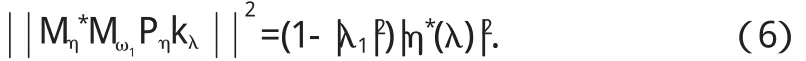
因此〈

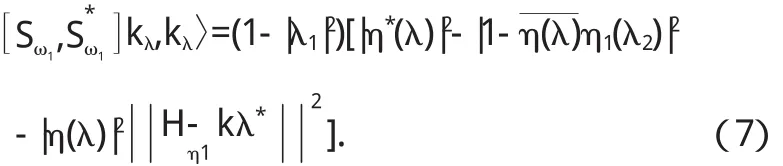
結合 η*的定義,對于任意

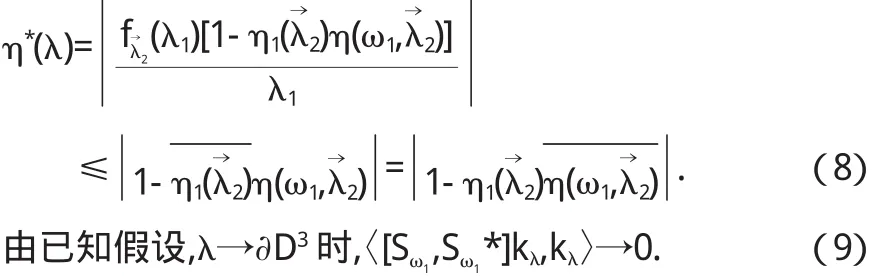
通過類似的證明方法,這個結果可以推廣到多圓盤.

定 理 2 設 η 是一個內函數,Beurling型商模 N本性正規,則，其中 m∈M且 φ(ω)是至多(1,1,L,1)階的多項式.

Guo和 Wang[6]后來發現，三圓盤及以上多圓盤的齊次商模不是本性正規的.根據定理 2,我們猜測三圓盤及以上多圓盤 Beurling型商模也不是本性正規的.

〔1〕R.Douglas,V.Paulsen,Hilbert Modules over Function Algebras [M].New--York:Longman Scientific& Technical,1989.

〔2〕W.Arveson,Quotient of standard Hilbert modules[J]. Transactions of the American Mathematical Society, 2007,359(12):6027-6055.

〔3〕R.Douglas,G.Misra,Some Calculations for Hilbert modules [J].Journal of O rissa Mathematical Society, 1993:1-11.

〔4〕K.Guo,K.Wang,Beurling type quotient modules over the bidisk and boun- -dary representations[J]. Journal of Functional Analysis,2009,257(10):3218-3238.

〔5〕W.Rudin,Function Theory in Polydiscs [M].New York:Benjam in,1969:110-114.

〔6〕K.Guo K,P.Wang,Essentially normal Hilbert modules and K-homology IV:Quasi-homogenous quotient modules of Hardy module on the polydisks[J].Science China Mathematics,2012,55(8):1613-1626.

O177

A

1673-260X（2014）08-0011-02