奇妙的斐波那契數列

于海杰

（赤峰學院 初等教育學院，內蒙古 赤峰 024000）

奇妙的斐波那契數列

于海杰

（赤峰學院 初等教育學院，內蒙古 赤峰 024000）

斐波那契數列在各領域都有廣泛的應用.本文簡單介紹了斐波那契數列的由來，斐波那契數列的簡單應用及自然界中的斐波那契數.

斐波那契數列；通項公式；性質；應用

1 問題的提出

定理 若 n∈N，

所以 a，b是方程 x2-x-1=0的兩個根，

則 a2=a+1，b2=b+1，所以

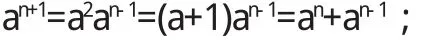
同理 bn+1=bn+bn-1.從而有

即 f(n)=f(n-1)+f(n-2)，n≥2.

于是 f(0)=1，f(1)=1，f(2)=f(0)+f(1)=2，f(3)=f(2)+f(1)=3，……都是正整數，定理得證.

從上述定理的證明不難看出：這是一個由自然數構成的數列，通項公式竟然是用無理數表示的；并且這個數列，前兩項都為 1，從第三項起，每一項都是前兩項之和，這個數列就是有名的斐波那契數列，又稱黃金分割數列.

2 斐波那契數列的由來

13世紀意大利數學家斐波那契在他的《算盤書》的修訂版中增加了一道著名的兔子繁殖問題.問題是這樣的:如果每對兔子（一雄一雌）每月能生殖一對小兔子（也是一雄一雌，下同），每對兔子第一個月沒有生殖能力，但從第二個月以后便能每月生一對小兔子.假定這些兔子都沒有死亡現象，那么從第一對剛出生的兔子開始，12個月以后會有多少對兔子呢？解釋說明為：一個月：只有一對兔子；第二個月：仍然只有一對兔子；第三個月：這對兔子生了一對小兔子，共有 1+1=2對兔子.第四個月：最初的一對兔子又生一對兔子，共有 2+1=3對兔子.則由第一個月到第十二個月兔子的對數分別是：1，1，2，3，5，8，13，21，34，55，89，144，……，后人為了紀念提出兔子繁殖問題的斐波納契，將這個兔子數列稱為斐波那契數列，即把 1，1，2，3，5，8，13，21，34…這樣的數列稱為斐波那契數列.

3 斐波那契數列的通項公式

由斐波那契數列的定義，可以知道斐波那契數列的各項之間有如下的關系：

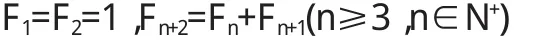
通過上面定理的證明可以得出斐波那契數列的通項公式為

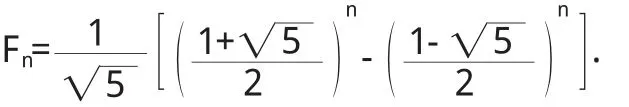
注意：這個公式又叫“比內公式”，正如前面所說這是用無理數表示有理數的一個范例.

4 斐波那契數列的性質

性質1若數列{Fn}為斐波那契數列，則；其中為黃金分割比.

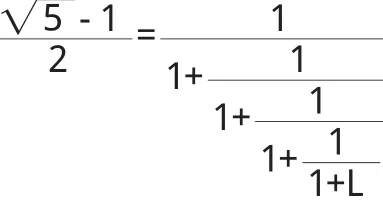
性質 2

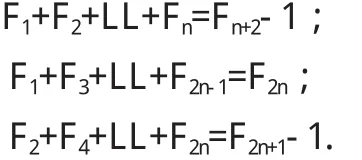
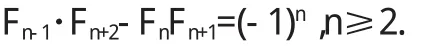
斐波那契數列還有許多其他性質，可參考相關研究文獻[3-5].

5 斐波那契數列的簡單應用

例 1(爬樓梯問題) 某人爬有 n個臺階的樓梯，規定每一步只能跨邁一個或兩個臺階，問這個人有多少種不同的爬樓方法？

解 設爬 n個臺階有 an種方法.登上第一級臺階有一種登法；登上兩級臺階，有兩種登法；登上三級臺階，有三種登法；登上四級臺階，有五種登法……

1，2，3，5，8，13……

考慮最后一步：若最后一步邁一個臺階，則前 n-1個臺階有 an-1種方法；若最后一步邁兩個臺階，則前n-2個臺階有an-2種不同的方法.于是，由加法原理得：an=an-1+an-2，可知其初值a1=1，a2=2，從而an=Fn+1(n>2).

例2比較a與b的大小關系，已知

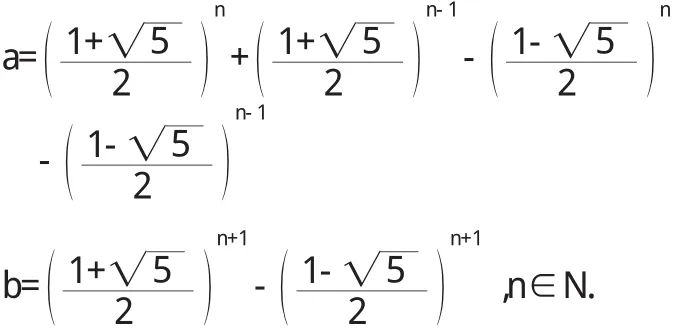
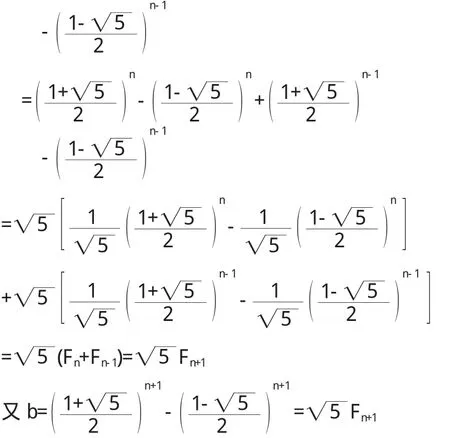
所以 a=b

例3現有長為150cm的鐵絲，要截成n(>1)段，每段的長為不小于1cm的整數，如果其中任意三小段都不能拼成三角形，試求n的最大值，此時有幾種方法將該鐵絲截成滿足條件的n段（第17屆江蘇省初三數學競賽題）.

解 欲使 n盡可能的大，則每段長應該盡可能的小，又由每段的長不小于1cm，所以應從1開始分截，假定含有1的起始三段長為1,b,c，且1≤b≤c，為了使這三段都不能構成三角形，則1+b≤c，又要滿足b,c盡可能的小，故取b=1,c=2，于是這n段可分截如下：

1,1,2,3,8,13,ΛΛ，這就是斐波那契數列，

又因為 1+1+2+3+5+8+13+21+34+55<150，

而 1+1+2+3+5+8+13+21+34+55+89>150，

故 n的最大值為 10，將長為 150cm的鐵絲分成滿足條件的10段共有如下7種方式：

⑴1、1、2、3、5、8、13、21、35、61

⑵1、1、2、3、5、8、13、21、36、60

⑶1、1、2、3、5、8、13、21、37、59

⑷1、1、2、3、5、8、13、21、34、62

⑸1、1、2、3、5、8、13、22、35、60

⑹1、1、2、3、5、8、13、22、36、59

⑺1、1、2、3、5、8、14、22、36、58

6 自然界中的斐波那契數

斐波那契數列中的任意一個數，都叫斐波那契數.斐波那契數是大自然的一基本模式，可以出現在許多場合.

6.1 樹木生長中的斐波那契數

一棵樹在一年后長出一個新枝，休息一年后再長出一個新枝，以后每個樹枝都遵循這樣的規律，于是第一年只有一個主干，第二年有兩個枝，第三年三個，第四年五個，以此類推，便構成了斐波那契數列.這個規律，就是生物學上著名的“魯德維格定律”.

6.2 花瓣數中的斐波那契數

大多數植物的花，其花瓣數都恰是斐波那契數.如蘭花、茉利花、百合花都是 3個花瓣，毛茛屬的植物有 5個花瓣，翠雀屬植物有 8個花瓣，萬壽菊屬植物有 13個花瓣，紫菀屬植物有 21個花瓣，雛菊屬植物有 34、55或 89個花瓣.

6.3 向日葵花盤內葵花子排列的螺線數

向日葵花盤內，種子是按對數螺線排列的，有順時針轉和逆時針轉的兩組對數螺線.兩組螺線的條數往往構成相繼的兩個斐波那契數，一般是34和55，大向日葵是89和144，還曾發現過一個更大的向日葵有144和233條螺線，它們都是相繼的兩個斐波那契數.

目前關于斐波那契數列的相關研究比較多，主要研究斐波那契數列的性質以及在各領域的應用，如斐波那契數列在數學、物理、化學甚至金融等領域的應用.美國數學會1960年出版了《斐波那契數列》季刊，專門發表有關斐波那契數列新發現和新用途的文章.可見，今后對于斐波那契數列的研究依舊前景廣闊.

〔1〕課程教材研究所數學課程教材研究開發中心.初等數論[M].北京：人民教育出版社，2003.

〔2〕于海杰.論連分數的應用[J].赤峰學院學報，2014（2）.

〔3〕凌曉牧.有趣的斐波那契數列[J].江蘇教育學院學 報，2011（10）.

〔4〕王君行．斐波那契數列的一些有趣的性質[J]．數學通報，2009（48）．

〔5〕林喜季．關于斐波那契數列的性質探討[J]．福建商業高等專科學校學報，2006（12）．

〔6〕李文林．數學史概論［M］.北京:高等教育出版社，2000．

〔7〕凌曉牧.有趣的斐波那契數列[J].江蘇教育學院學 報，2011（10）.

O151

A

1673-260X（2014）08-0001-02