基于NX的斜齒輪滾齒加工仿真系統設計*

張榮闖，王 軍，王宛山

(東北大學 機械工程與自動化學院，沈陽 110819)

基于NX的斜齒輪滾齒加工仿真系統設計*

張榮闖，王 軍，王宛山

(東北大學 機械工程與自動化學院，沈陽 110819)

為建立滾齒加工幾何仿真與反應加工過程的物理模型之間的聯系，提出了基于NX二次開發的斜齒輪滾齒加工仿真方法。首先構建了斜齒輪滾齒加工仿真系統總體結構；其次，建立了滾齒加工過程的運動學方程；然后，對工件幾何實體、滾刀掃掠體、齒廓實體以及未變形切屑幾何實體構建過程進行了描述；最后，對一個實例斜齒輪進行仿真加工，仿真法向齒廓與理論漸開線齒廓的比較驗證了所提出方法的合理性與準確性。

滾齒加工；幾何仿真；未變形切屑；二次開發

0 引言

齒輪虛擬加工是齒輪精確建模的主要方法，同時也是研究齒輪加工過程的重要手段。目前，國內外研究者已經能夠通過計算機編程來實現齒輪虛擬加工。蒲太平[1]、汪中厚[2]等人為實現齒輪三維精確建模，利用CATIA V5的二次開發功能構建出齒輪虛擬加工系統。徐銳[3]、周太平[4]等利用AutoCAD二次開發技術，完成了滾齒加工過程仿真，實現了齒輪三維精確建模，并對滾刀設計的準確性進行仿真切齒驗證。熊越東[5]等基于VC與AutoCAD 聯合開發環境提出了準雙曲面齒輪控加工幾何仿真的基本實現方法，建立了準雙曲面齒輪數控加工仿真系統，實現其精確幾何建模。K.-D. Bouzakis[6]、Orestis Friderikos[7]等利用編程語言MATLAB開發出滾齒加工幾何仿真系統，并且將其幾何仿真結果應用于所建立的基于有限元物理仿真模型，仿真結果揭示了滾齒切屑復雜流動機制、闡釋了滾刀刀齒崩刃現象的原因。Vasilis D[8]、Tapoglou N[9-10]等基于CAD實現了滾齒加工過程仿真，仿真結果不僅輸出齒輪幾何模型，同時也實現了未變形切屑精確建模，并將其應用于動態滾切力預測。由上可知，在齒輪加工仿真方面，國內研究局限于齒輪幾何建模、仿真切齒實驗等幾何仿真，而國外在幾何建模研究的基礎上，能夠將幾何仿真結果與物理模型進行聯系，實現對齒輪加工過程機理的深入研究。綜上，本文以NX為建模平臺，利用其方便的二次開發功能模擬真實滾齒加工過程，開發出斜齒輪加工仿真系統；該系統實現了斜齒輪幾何精確建模，同時也提取出工件材料去除過程中形成的未變形切屑，為滾齒加工過程物理模型的建立奠定基礎。

1 仿真系統架構

本文開發的斜齒輪滾齒加工仿真系統建立在Windows開發平臺下，使用Visual Studio 2008編程工具、matlab數值計算工具以及NX軟件二次開發模塊建立起來的。

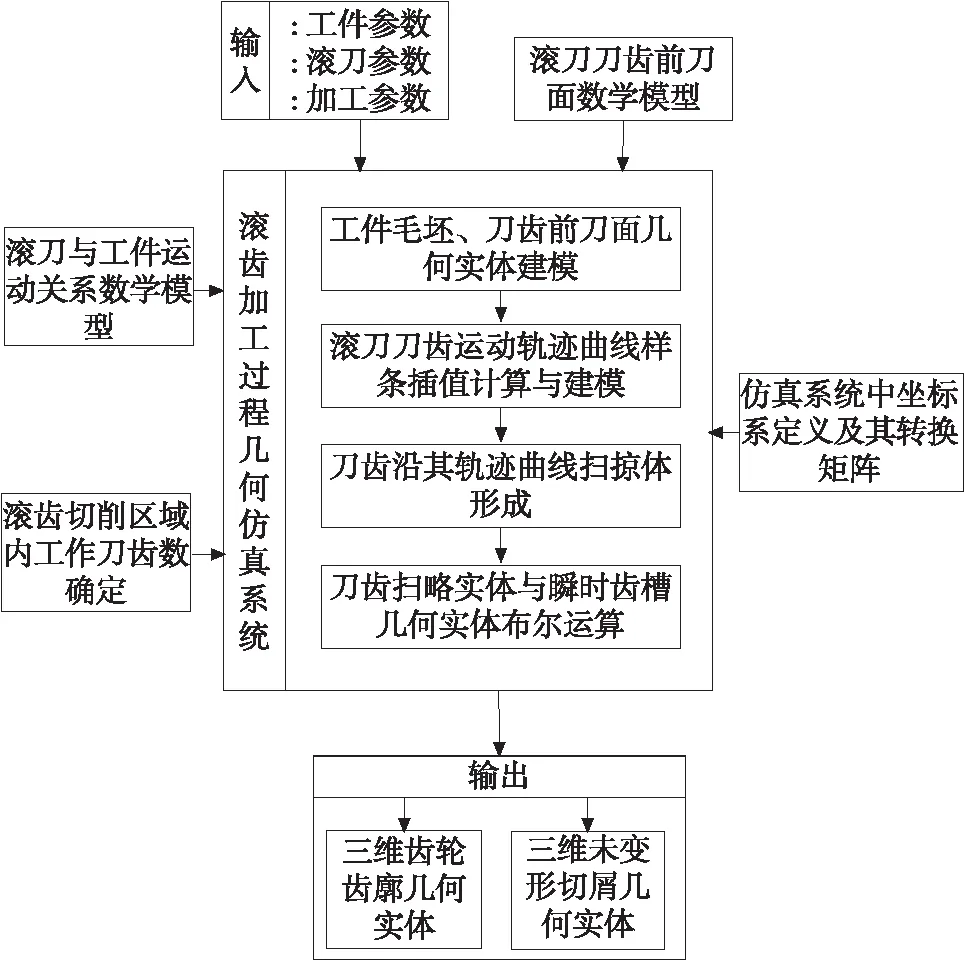
圖1 仿真系統總體結構

圖1所示為仿真系統總體結構圖。當輸入加工參數之后，仿真系統將自動創建工件幾何實體，求解滾刀刀齒前刀面數學模型并對其進行空間幾何建模。同時，程序也將求解出滾刀工作刀齒數目。依據滾刀和工件之間的運動關系、位置關系確定每個工作刀齒在切削過程中所走過的刀齒運動軌跡并對其進行空間曲線精確建模。刀齒前刀面幾何模型與刀齒運動軌跡曲線聯合生成滾刀刀齒掃掠體，刀齒掃掠體與瞬時齒槽幾何實體之間的布爾運算形成未變形切屑以及新的瞬時齒槽。仿真結束后將輸出各個刀齒在展成切削過程中去除的未變形切屑以及最終齒輪齒廓幾何模型。

2 仿真系統加工運動模型的構建

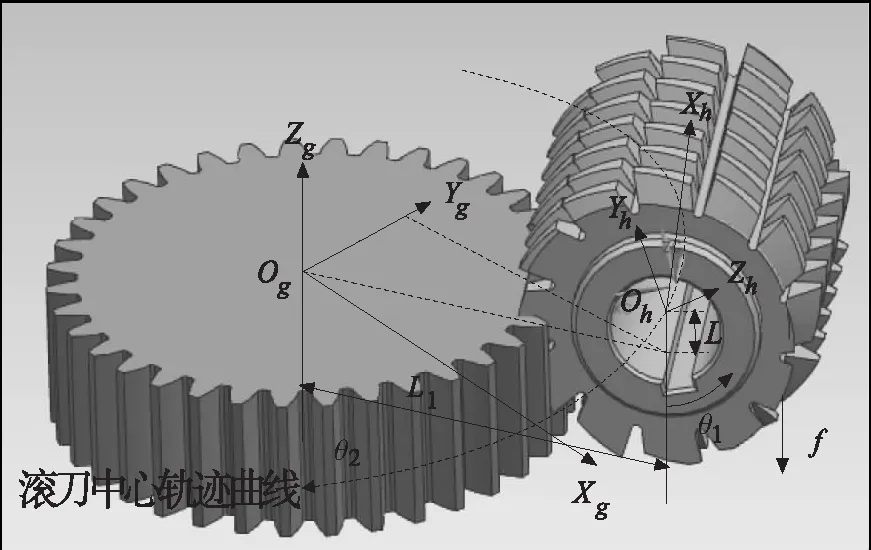
圖2 滾齒加工示意圖 表1 滾齒加工工藝參數

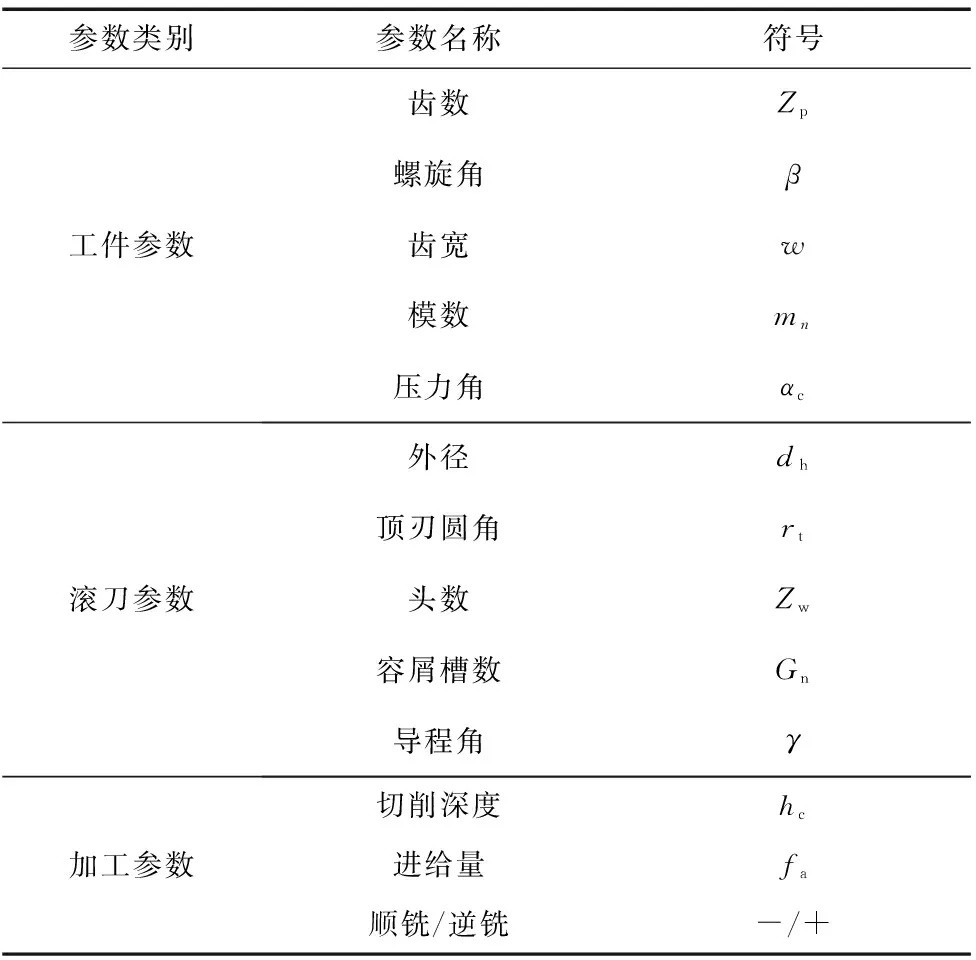
參數類別參數名稱符號工件參數齒數Zp螺旋角β齒寬w模數mn壓力角αc滾刀參數外徑dh頂刃圓角rt頭數Zw容屑槽數Gn導程角γ加工參數切削深度hc進給量fa順銑/逆銑-/+

研究采用零前角單頭右旋標準齒輪滾刀，以逆銑方式對右旋斜齒輪進行加工。表1為滾齒加工過程中的所涉及的工藝參數。圖2所示為滾齒加工示意圖。為了方便滾齒加工過程數學模型建立，假設工件靜止不動，滾刀既繞其自身軸線旋轉，又圍繞工件做螺旋運動。加工斜齒輪，滾刀繞其自身軸旋轉角度為θ1時，其繞工件軸旋轉過的角度為θ2，沿工件軸線進給長度為f，三者之間的關系如下：

θ2=K1θ1,K1=(1/Zp)/{1-ftsinβ/(πmnZp)}

f=K2θ2,K2=ft/(2π)

(1)

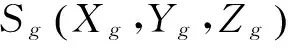
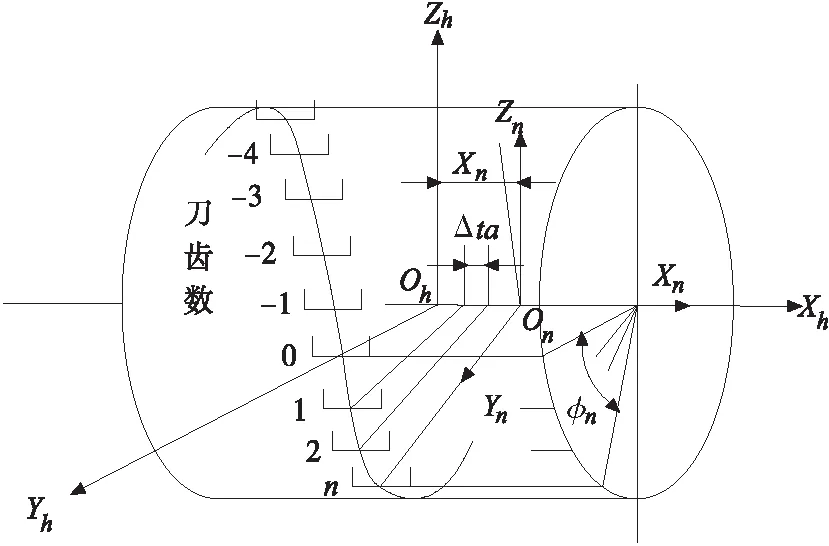
圖3 滾刀刀齒坐標系

設定滾刀位于創成中心的刀齒為0號刀齒，前列及后列的刀齒編號如圖3所示。0號刀齒坐標系與滾刀坐標系相重疊,n號刀齒坐標系與滾刀坐標系的相對位置可通過其與0號刀齒之間的軸向間距xn與相位角φn來表示：

xn={πmn/(Gncosγ)}n

(2)

φn=(2π/Gn)n

(3)

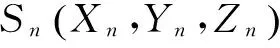
(4)

(5)

3 仿真系統中幾何模型構建

齒輪毛坯幾何實體構建：斜齒輪毛坯采用圓柱體，根據加工齒輪的齒數Zp、模數mn以及齒寬w要求確定出圓柱體的底面半徑和高度，進而通過NX二次開發函數UF_MODL_create_cyl1創建毛坯幾何實體。

滾刀刀齒掃掠體構建：工件材料去除過程，實際上是滾刀每個刀齒去除材料的過程；仿真中刀齒切削去除的材料可視為刀齒掃掠體與瞬時齒槽幾何實體之間的重疊幾何實體。如圖4所示，滾刀刀齒掃掠體由刀齒前刀面幾何模型沿其運動軌跡曲線掃略所形成的幾何體。刀齒前刀面由滾刀的幾何參數確定，運動軌跡是刀齒前刀面頂刃中點K在滾刀運動過程中相對于工件運動所走過的軌跡。滾刀刀齒掃掠體由NX二次開發函數UF_MODL_create_sweep創建。

齒廓實體與切屑實體的構建：如圖所示為滾刀刀齒掃掠體與瞬時齒槽幾何實體，它們之間進行求交和求差運算，分別形成此時參與切削刀齒所形成的未變形切屑與下一個刀齒切削時的瞬時齒槽；所有刀齒切削完成后，形成最終的齒輪齒廓幾何實體。

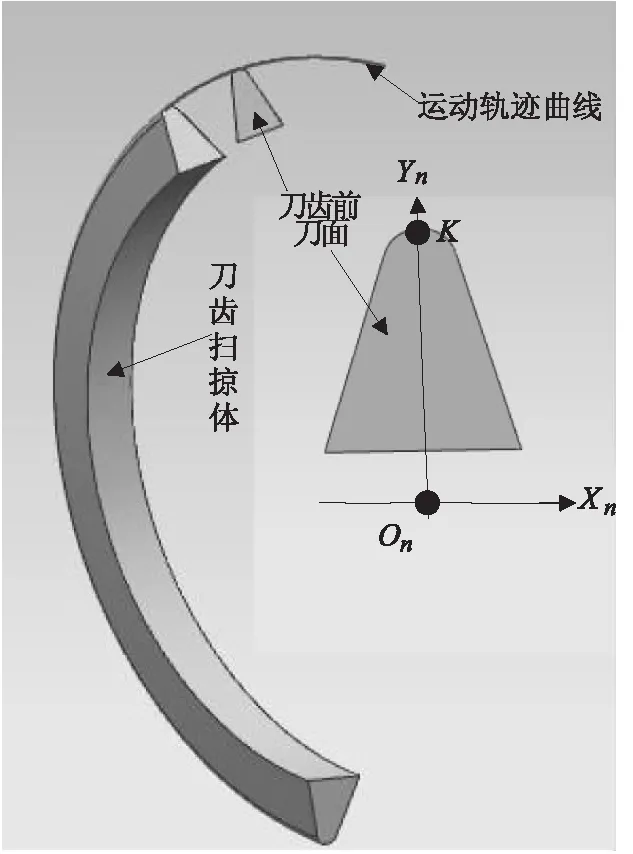
圖4 滾刀刀齒掃掠體

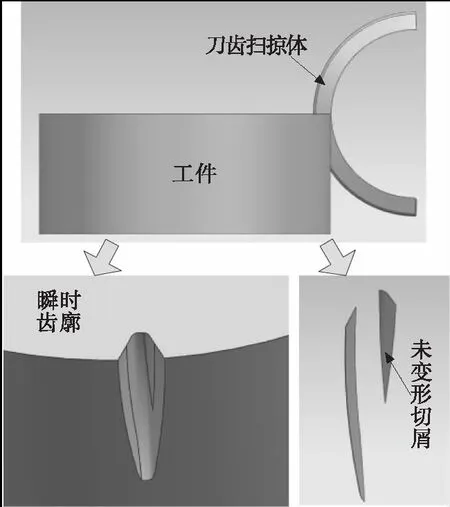
圖5 瞬時齒槽與未變形切屑

4 仿真實例

仿真刀具采用GB/T 6084 2001標準齒輪滾刀，斜齒輪參數為：模數mn=3，齒數Zp=36，壓力角α=20°，螺旋角β=15°，進給量1mm/rad，hc=全齒深。

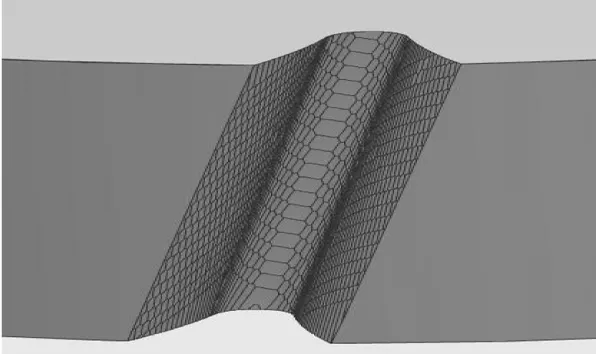
圖6 斜齒輪幾何模型

圖7 仿真齒輪法向截面齒廓

圖6所示為加工仿真之后所形成的斜齒輪幾何模型；圖7為斜齒輪法向齒廓；在UG二次開發環境下提取出齒輪法向齒廓線數據點，并在matlab軟件中對其進行曲線擬合，將擬合后形成的仿真法向齒廓曲線和理論漸開線齒廓進行比較。如圖8所示為仿真齒廓在加工過程中不考慮任何外在誤差引入、即理想加工狀態下相對于理論漸開線的滾刀刀齒截斷誤差的分布曲線，誤差值在0.7μ～0.9μ之間，說明本文所采用仿真方法準確性與合理性。表2所示為不同刀齒在其展成位置時所形成的未變形幾何切屑。

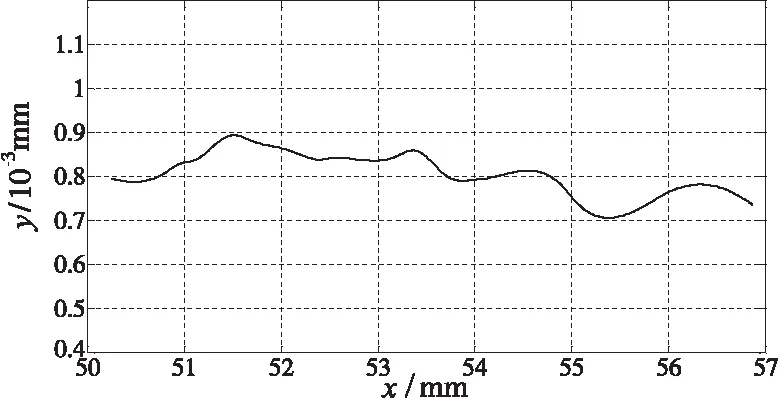
圖8 仿真齒廓與理論齒廓之間的誤差分布 表2 未變形切屑

N-17-16-15-14-13-12切屑幾何N-11-10-9-8-7-6切屑幾何N-5-4-3-2-1切屑幾何N01234切屑幾何N56789切屑幾何N10111213切屑幾何

5 結論

基于NX二次開發技術，建立了斜齒輪滾齒加工仿真系統；斜齒輪仿真法向齒廓與理論漸開線對比說明本文所采用方法的合理性與準確性。所開發的系統可以用于滾刀設計合理性檢驗，仿真齒廓為齒輪接觸特性和有限元分析提供精確的三維幾何模型；提取出的未變形幾何切屑包含滾刀切削刃幾何邊界參數，可以用作滾齒加工過程動態切削力、滾刀磨損的預測以及優化工藝參數。

[1] 蒲太平, 唐進元. 基于 CATIAV5 的圓柱齒輪虛擬加工研究[J]. 系統仿真學報, 2008, 20(16): 4339-4343.

[2] 汪中厚, 李剛, 張興林, 等. 漸開線斜齒輪整體虛擬滾齒仿真及齒面精度研究[J]. 機械傳動, 2012,36(8): 9-13.

[3] 徐銳, 陳兵奎, 王振榮. 運用 AutoCAD 的滾齒加工仿真[J]. 現代制造工程, 2011 (7): 66-69.

[4] 周太平, 謝世坤, 康志成. 多種圓柱齒輪仿真切削建模及測量[J]. 機械傳動, 2013, 37(4): 118-121.

[5] 熊越東, 王太勇, 劉富凱, 等. 準雙曲面齒輪數控加工仿真系統設計[J]. 組合機床與自動化加工技術, 2005(7): 43-45.

[6] Bouzakis K D, Friderikos O, Tsiafis I. FEM-supported simulation of chip formation and flow in gear hobbing of spur and helical gears[J]. CIRP Journal of Manufacturing Science and Technology, 2008, 1(1): 18-26.

[7] Friderikos O, Maliaris G, David C N, et al. An investigation of cutting edge failure due to chip crush in carbide dry hobbing using the finite element method[J]. The International Journal of Advanced Manufacturing Technology, 2011, 57(1-4): 297-306.

[8] Vasilis D, Nectarios V, Aristomenis A. Advanced computer aided design simulation of gear hobbing by means of three-dimensional kinematics modeling[J]. Journal of Manufacturing Science and Engineering, 2007, 129(5): 911-918.

[9] Tapoglou N, Antoniadis A. CAD-based calculation of cutting force components in gear hobbing[C]//DTMM 2010 international conference design, technology and management in manufacturing. Iasi (Romania). 2010: 14-16.

[10] Tapoglou N, Antoniadis A. Hob3D: a novel gear hobbing simulation software[C]//World congress on engineering. 2011: 6-8.

(編輯 趙蓉)

Design on Helical Gear Hobbing Machining Simulation System Based NX

ZHANG Rong-chuang, WANG Jun, WANG Wan-shan

(School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819，China)

To establish the link between geometric simulation and physical simulation model for gear hobbing, simulation approach of the hobbing process for the manufacturing of helical gears based on NX secondary development was put forward. General structure of helical gear hobbing simulation system was developed; the kinematics equation for gear hobbing cutting process was established; the creation processes of workpiece geometric entity, swept geometric entity of the hob tooth and undeformed chip geometric entity were described; The confirmation of the validity and accuracy of the proposed method has been accomplished by comparison between the produced helical gear gap normal profile and theoretical ones.

hobbing machining ; geometry simulation; undeformed chip; secondary development

1001-2265(2014)06-0093-04

10.13462/j.cnki.mmtamt.2014.06.026

2014-02-16;

2014-03-12

國家863高技術研究發展計劃(2012AA041303)

張榮闖(1984—)，男，遼寧遼陽人, 東北大學博士研究生，主要研究方向為數字化設計與制造(E-mail)zhangrongchuang@126.com；王軍(1956—)，男，沈陽人，東北大學教授，博士，博士生導師，主要研究方向為數字化制造、先進數控理論；王宛山(1946—)，男，沈陽人，東北大學教授，博士生導師，主要研究方向為數字化制造、精密加工。

TH162;TG506

A