平面NURBS曲線的等距線有理逼近算法*

蔡天賜，趙玉剛，王占軍，劉新玉

(山東理工大學 機械工程學院，山東 淄博 255049)

平面NURBS曲線的等距線有理逼近算法*

蔡天賜，趙玉剛，王占軍，劉新玉

(山東理工大學 機械工程學院，山東 淄博 255049)

基于NURBS曲線導矢的計算公式，首先給出了平面NURBS曲線精確等距線的生成算法, 這種算法穩定可靠、計算精度高，但它生成的等距線不再是有理多項式形式。根據等距曲線逼近的關鍵在于參數速度模的逼近,因此利用函數的連分式展開式實現其逼近，在此基礎上導出平面NURBS曲線的等距線有理逼近算法。最后的實例驗證了所提算法的可行性與有效性。

NURBS曲線；等距線；參數速度；連分式；有理逼近

0 引言

曲線曲面的等距計算是CAD/CAM系統中的一個重要幾何運算，在NC加工、機構運動學、道路設計等領域中有著廣泛的應用，因此受到眾多學者的重視，研究文獻豐富。

等距曲線的逼近算法主要有：控制頂點偏移法[1-2]、包絡方法[3]、基于插值或擬合的方法[4-5]等。這些方法對等距曲線進行了各類有效的逼近, 但仍存在著不少的缺陷：目前大部分等距逼近曲線通常為多項式表示，這往往導致逼近曲線的次數相當高, 或需對原曲線進行多次離散, 因而需要大量的數據存儲；目前很多方法所得的等距逼近曲線已不再是基曲線沿法矢方向平移一定距離的點的軌跡，當用戶需改變等距距離時, 系統必須從頭開始重新生成逼近曲線，這對于交互操作相當不利。

基于NURBS曲線導矢的計算公式，本文首先給出了平面NURBS曲線精確等距線的生成算法。在研究連分式理論的基礎上，通過對NURBS曲線的參數速度模的有理逼近，完成了平面NURBS曲線的等距曲線的有理逼近。算法所得的等距逼近曲線將保持基曲線法矢的平移方向,當用戶改變等距距離時, 也不需要重新運行逼近程序, 只需利用原逼近的信息就可快速生成新的等距逼近曲線。另外, 這種等距逼近程序只需運行一次即夠, 因而計算量和存儲量大為減少。最后的應用實例驗證了所提算法的合理性和有效性。

1 基于導矢的NURBS曲線精確等距線生成算法

1.1 NURBS曲線定義

一條k次NURBS曲線可以表示為一分段有理多項式函數：

(1)

其中，di(i=0,1,…,n)是控制點，ωi是權因子，每一個控制頂點di都附有一個權因子ωi，首末權因子ω0，ωn>0其余ωi>0。Ni,k(u)是定義在非周期且非均勻節點矢量U上的k次B樣條基函數，它可由以下的Cox-deBoor遞推公式求得：

(2)

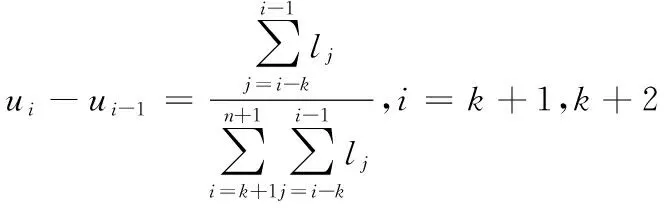
(3)

其中：li=|di-di-1|(i=1,2,...,n)為控制多邊形各邊長。

1.2 NURBS曲線精確等距線生成算法

給定正則平面NURBS曲線：P(u)=(x(u),y(u))，其參數速度P′(u)及其模長σ(u)分別被定義為：

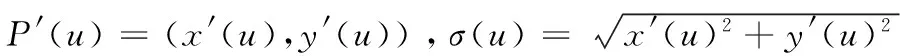
由此得到基曲線距離為d的等距曲線Pd(u)為：

(4)

其中N(u)是P(u)上對應參數u處的單位法矢量。

由(4)式可知要計算N(u)需要計算參數速度P′(u)，對1.1節中(1)式求導有：

(5)

計算P′(u)的關鍵是對k次B樣條基函數求導，由1.1節中(2)式可得基函數導數的遞推公式：

(6)

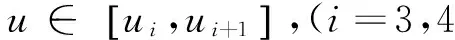
(7)

其中：

由(1)～(3)式和(4)～(6)式可生成任意次NURBS曲線與其精確等距曲線，結合(7)式，則可快速求出常用的三次NURBS曲線的精確等距線。

2 連分式的NURBS等距線有理逼近算法

由第1節中算法，可以計算出平面NURBS曲線的精確等距線，但是由等距曲線的計算表達式可見，在計算單位法矢量N(u)時，參數速度模σ(u)需要進行開方運算，因而σ(u)不再是用多項式表示，這導致NURBS曲線的等距線不再具有有理多項式形式。為了保持CAD/CAM造型系統中數據結構和幾何算法的統一性，本節利用函數的連分式展開式對σ(u)進行逼近，進而導出了NURBS曲線的等距曲逼近算法。

2.1 函數的連分式展開

根據連分式理論中的逐次迭代算法可將一個給定的函數f，轉變成如下形式的連分式：

(8)

若用Rn表示上述展開式的前n項截斷，令Rn=Pn/Qn，由連分式的性質可以得到如下的遞推關系:

(9)

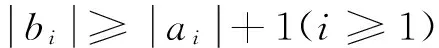
(10)

(11)

2.2 NURBS曲線的等距線有理逼近算法

由上面的論述可知，如何進行NURBS曲線的等距線有理逼近，轉化為如何用有理形式來近似表示參數速度模σ(u)。

首先對(10)、(11)式取前n項截斷得：

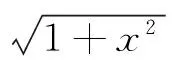
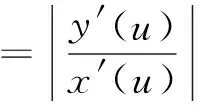
(12)

(13)

最后結合1.2節中(4)式即可導出與基曲線P(u)的等距曲線Pd(u)相對應的有理逼近曲線：

(14)

(15)

(16)

(17)

3 NURBS曲線等距線生成算法實例

基于C++ Builder可視化的開發環境，通過自主編程，對1.2節和2.2節中的算法進行了仿真驗證。

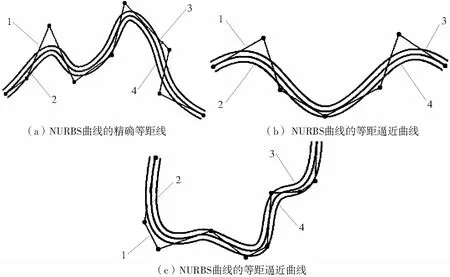
圖1 9個控制點NURBS曲線效果圖

圖1a所示為9個控制點按1.2節算法生成的三次NURBS曲線的精確等距線效果。圖1b、1c所示分別為7個控制點按2.2節算法(14)式、10個控制點按按2.2節算法(15)式所得的等距逼近效果，截斷次數取為5。其中，每個控制頂點對應的權因子為1。圖1中1號曲線代表控制點構成的控制多邊形，2號曲線代表三次NURBS基曲線，圖1a中3號、4號曲線代表沿法線正、負方向得到的NURBS曲線的精確等距線。圖1b、1c中3、4號曲線則代表沿法線正、負方向得到的NURBS曲線的等距逼近曲線。

圖2a、2b所示為5個相同控制點按2.2節算法中(14)式、(15)式所得的等距逼近效果，截斷次數取3，等距距離d=1。1號曲線代表控制點構成的控制多邊形，2號曲線代表NURBS基曲線，3號實線代表NURBS曲線的等距逼近曲線，4號虛線代表NURBS曲線的精確等距線。通過改變截斷次數，(14)式和(15)式兩種方法所對應的等距逼近誤差ε1(u)和ε2(u)則如表1所列。

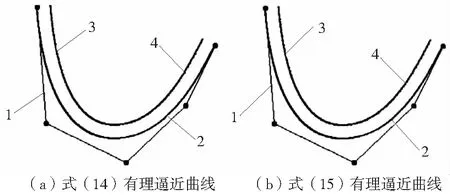
圖2 5個控制點生成的NURBS曲線效果圖 表1 NURBS曲線的等距逼近誤差

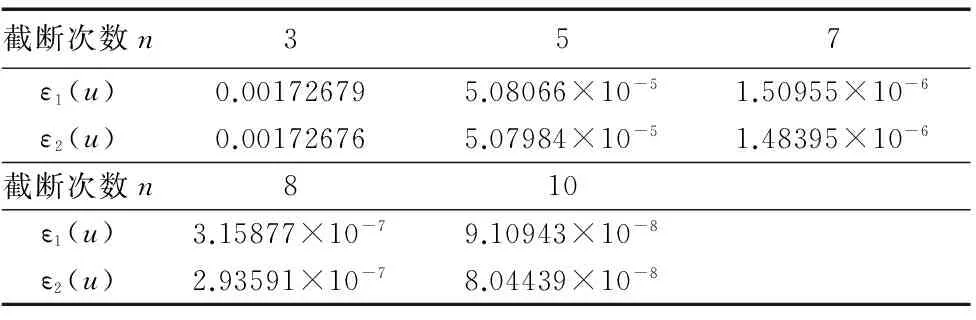
截斷次數n357ε1(u)0.001726795.08066×10-51.50955×10-6ε2(u)0.001726765.07984×10-51.48395×10-6截斷次數n810ε1(u)3.15877×10-79.10943×10-8ε2(u)2.93591×10-78.04439×10-8

4 結束語

本文首先給出了基于NURBS曲線導矢的NURBS曲線精確等距線的生成算法，這種算法精確、穩定、高效，基曲線的兩條等距曲線能夠同時給出，一氣呵成。但其缺點是生成的NURBS曲線的等距線不再具有有理多項式形式。

基于NURBS曲線的參數速度模是導致等距線不再是有理多項式這一觀察，在研究連分式理論的基礎上，通過對參數速度模的有理逼近，完成了平面NURBS曲線的等距線的有理逼近。由最后的仿真實例可以看到，等距曲線逼近效果良好，算法所得的等距逼近曲線仍舊保持基曲線法矢的平移方向，和原等距曲線之間的誤差很小，并且隨著截斷次數的增大，逼近誤差不斷減小。

[1] Cobb, E.S. Design of sculptured surfaces using the B-spline representation．Ph.D. Dissertation, University of utah. USA. Jun.1984．

[2] Tiller,W., Hanson, E.G., Offsets of two-dimensional profiles.IEEE Computer Graphics and Application, 1984,4(9):36-46.

[3] Lee,I.K., M.S., Elber,G... Planar curve offset based on circle approximation. Computer Aided Design , 1996, 28(8):617-630．

[4] Klass, R.An offset spline approximation for plane cubic splines. Computer Aided Design,1983,15(5) : 97-299.

[5] Piegl, L.A., Tiller,W. Computing offsets of NURBS curves and surfaces. Computer Aided Design, 1999,3l(2):147-156．

[6] Hoschek J. Spline approximation of offset curves. Computer Aided Geometric Design,1988, 5(1):34-40．

[7] De Boor C. On calculating with B-splines. Journal of Approximation Theory, 1972, 2: 50-62.

[8] Les Piegl, Wayne Tiller. The NURBS BOOK [M]. Second Edition. Beijing: Tsinghua University Press, 2010.

[9] 朱心雄. 自由曲線曲面造型技術[M].北京:科學出版社, 1999.

[10] 陳國棟,成敏,王國瑾.基于參數速度逼近的等距曲線有理逼近[J].計算機學報.2002,25(9):1001-1007.

[11] 王仁宏,朱功勤. 有理函數逼近及其應用[M].北京:科學出版社，2004．

[12] 張偉紅.平面Bezier曲線的等距曲線有理逼近[D].合肥: 合肥工業大學,2006.

(編輯 趙蓉)

The Rational Approximation Algorithm of Planar NURBS Curve and Its Offset

CAI Tian-ci, ZHAO Yu-gang, WANG Zhan-jun, LIU Xin-yu

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255049,China)

Based on the derivatives of NURBS curve, the generation algorithm of offset curve is proposed. This algorithm is stable, reliable and accurate, but the offset curve it generates is no longer a rational polynomial form. According to the crux of offset curve approximation lies in the approximation of parametric speed, the rational approximation method of the norm of parametric speed based on the function of continued fraction expansion is provided. On that basis, the rational approximation algorithm of offset curve is derived. The final examples verify the feasibility and effectiveness of the proposed algorithms.

NURBS；offset curve；parametric speed; continued fraction; rational approximation

1001-2265(2014)06-0035-03

10.13462/j.cnki.mmtamt.2014.06.010

2013-09-17；

2013-10-12

國家自然科學基金項目(51375285)

蔡天賜(1988—)，男，山東臨沂人，山東理工大學碩士研究生，研究方向為數控技術及機電一體化，(E-mail)caiti.anci@163.com；通訊作者：趙玉剛(1964—)，男，山東萊蕪人，山東理工大學教授、博士生導師，博士，研究方向為數控技術、機電一體化與特種加工技術，(E-mail)zhanggy9289@126.com。

TH161;TG65

A