液化天然氣低溫貯存分層研究

韓一飛

(西安航空學院 動力工程系，陜西 西安 710077)

1 引言

在低溫液體停放和運輸階段中，液體內部會出現溫度分層現象。研究分層現象下溫度分布的方法有三種，即實驗、理論和數值模擬。由于低溫液體儲罐內的溫度不易測量，且實驗方法獲得的數據誤差大，特別是在宇航領域，對于裝有液氫、液氧的密閉燃料室，溫度熱分層現象更加不易測量。因此，合理建立模型，科學簡化，通過理論分析計算儲罐內溫度分布解析解，帶入具體工業實踐參數，對結果進行分析并證實其有效性，從而為后續利用Fluent軟件進行大量數值模擬提供參考對比的實際意義。

在以上認識的前提下，本文以100%純甲烷為例，建立分層幾何模型，列出數學模型，對模型簡化求得純甲烷在儲罐內溫度分布的理論解析解。并從工業實踐中獲得液化天然氣儲罐的具體尺寸參數和環境參數，帶入解析解，從而計算儲罐內不同高度下各點經過不同時刻溫度值。最后，對計算結果進行分析，總結溫度分布規律。結果表明，規律與已有大量文獻研究結論吻合，該方法所得解析解是有價值的。

2 構建模型

2.1 原始數據

LNG容器：圓柱形豎放，內徑10m，高12m；材料：不銹鋼，外表珠光砂絕熱20mm厚；常壓；氣體純度：100%CH4。

2.2 理論基礎

建立分層幾何模型。為便于理解繪制了分層模型示意圖，如圖1所示：

圖1 液化氣分層模型示意圖

(1)分層模型

本模型假設，靠近儲罐壁面的液體首先受熱自然對流上升，在液體上部形成溫度分層區。分層區內的溫度呈上高下低的冪次分布。由于熱量隨液體的流動不斷傳人，因此分層區不斷加厚。為了求解分層區的形成過程，首先需要知道自然對流的發展。自然對流邊界層的動量與能量方程如下。

動量方程：

(2-1)

能量方程：

(2-2)

將式(2-1)和式(2-2)的邊界層溫度和速度無量綱化，同時假設邊界層厚度和特征速度的分布為δ=a1xm1，U=a2xn1。求解得到a1、a2、m1和n1，可以得出液體分層區厚度隨時間的變化規律。同時，分層區的溫度分布符合冪次分布E(Z)=mZn(m，n，為常數，Z為分層區底部以上的高度)。利用該式可以求出溫度分布式為：

(2-3)

式中 A——受熱面積；

δσ——分層區總高度；

Z——距離分層區內底部的高度；

t——加熱時間。

從而可以計算得到儲罐內相應的壓力。

(2)LNG儲罐周壁在環境漏熱情況下的熱流密度。

取環境溫度20℃，即為293.5K，空氣的對流換熱系數為h0=7.6W/m2K，取珠光砂的導熱系數為λ=0.05W/m·K。在0.1MPa的時候，純甲烷的飽和溫度t=111.51K。在0.6Mpa的時候，純甲烷的飽和溫度t=138.73K。在這一分層模型中，因為儲罐內的對流換熱系數較大，所以忽略其對流換熱熱阻，與此同時忽略不銹鋼壁的導熱熱阻。

下式中，A0是圓柱體外徑下的周壁面積，A是內徑下的周壁面積。

所以傳熱量Φ=kA0(293.5-111.51)=qwA

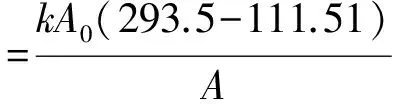
=343.2174W/m2

3 溫度分布計算及分析

本文對100%純甲烷儲罐內的溫度分布的計算基于(2-3)式，在開始時刻，即在0.1Mpa時，整個儲罐處于平衡均相狀態，全場溫度都對應0.1Mpa的飽和溫度。根據圓柱儲罐的對稱性，我們可以得知圓柱儲罐的中心軸線就是其內部溫度分布的對稱線。這一模型中，儲罐壁面在漏熱的情況下形成分層，隨著儲罐內液氣分界面處液體的蒸發，其上部的氣腔的壓力會一直增大，直到增大至0.6Mpa。但是因為這是一非定常過程，即在這一時間段內，這一氣腔內的壓力值是一直在變化的，為了簡化這一復雜模型。我們假設在一瞬間氣腔內的壓力達到0.6Mpa。這樣儲罐內的氣液分界面處的溫度瞬間達到138.73K，即0.6Mpa對應的飽和溫度。此后熱量不斷向液相區底部滲入，隨著時間的延續，直到最終整個儲罐內達到新的平衡均相狀態。在計算過程中，由于溫度是一直在變化的，所以其物性參數也是一直在變化的。所以在公式(2-3)的應用過程中，通過軟件可以獲得100%天然氣在任意溫度、0.6Mpa定壓下的ρ，c值，帶入公式，便可以求出儲罐不同高度，及經過不同時間后溫度大小。

3.1 各高度下隨時間變化溫度的增加值

把經歷不同時間長短后的溫度增加值制作如表1，并畫出相應的圖形曲線，如圖2所示。這一圖示中橫坐標表示經過一段時間后，儲罐內部的某一高度下的溫度值在0.1Mpa時最初均勻溫度場111.51K的差值。

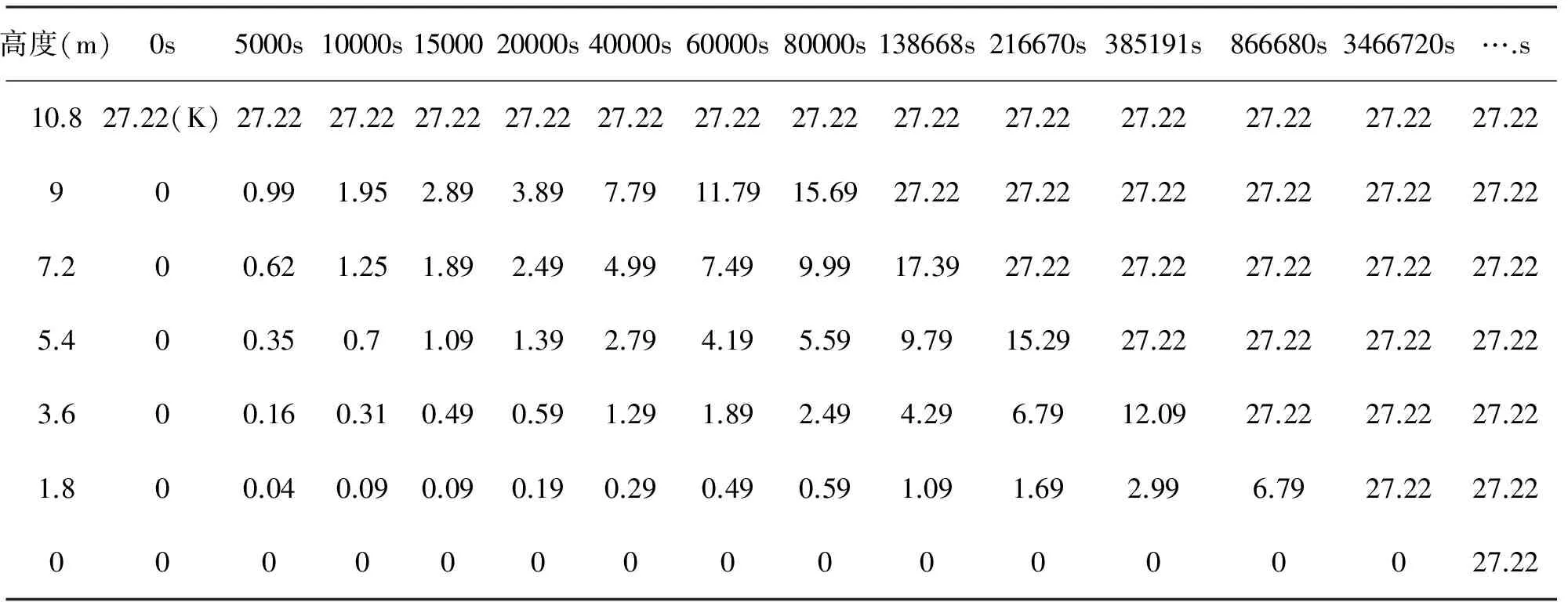
表1 純甲烷情況下經過一段時間后液相區不同高度下溫度增加值

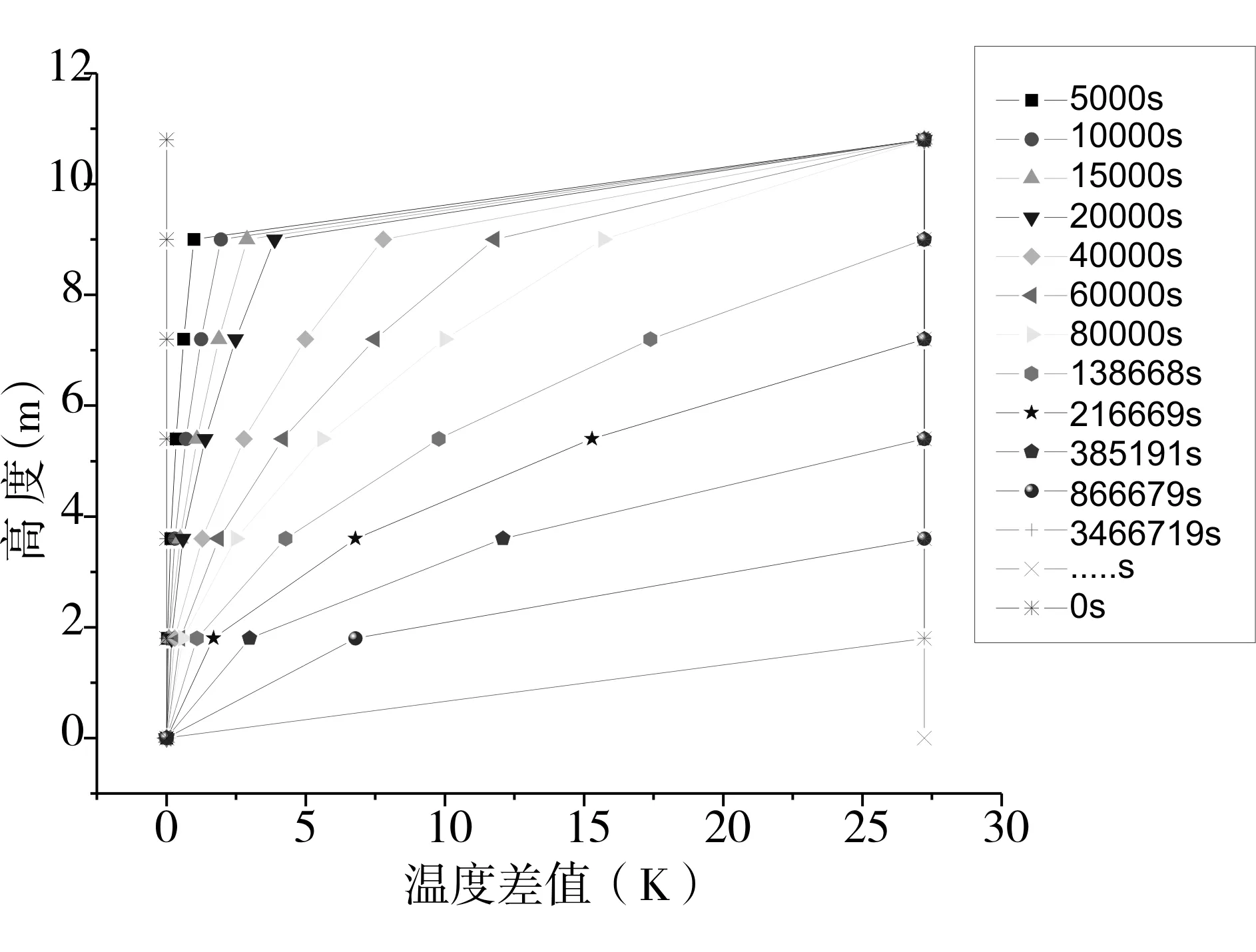
圖2純甲烷情況下經過一段時間后

液相區不同高度下溫度增加值

隨著時間的變化，氣液分界面處的溫度會一直保持不變，即138.73K，而其他較低高度下隨著時間增大都會相繼達到138.73K，當時間趨向無窮大的時候，整個溫度場會變得均勻，即0.6Mpa對應的飽和溫度。

3.2 經過特定時間，各高度下溫度大小

在LNG的存儲和運輸過程中，由于分層現象的存在，從而使得在液相區的上部，其溫度變化越快，熱流更多的向上流動，進入儲罐的能量更多的集中于液體上部的分層區，使溫度呈現上高下低的特點。

由表2數據，繪制經過特定時間，各高度具體溫度值的曲線。發現經相同時間后，液相區上部的溫度值較大。隨著時間的延續，液相區的溫度值不斷增大，最終保持138.73K不變。此后，液相區的上部的等高度下，其溫度變化為0K，但下部等高度位置沒有達到138.73K，溫度隨時間會繼續增大直到138.73K。高度越高，其達到138.73K所用時間越短。溫度變化規律如圖3所示：

表2 液相區各高度下在經過10000s，20000s，40000，80000，138668s，385191s，3466719后的溫度值后的溫度值

圖3經過特定時間，各高度溫度值

3.3 經過不同時間，特定高度下溫度大小

表3 在10.8m，9m，5.4m，1.8m下經過不同時間后的溫度值

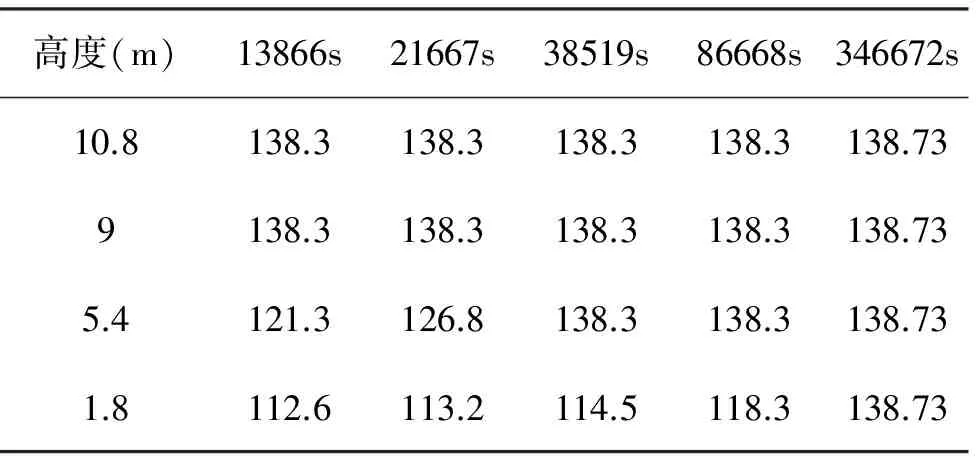
表3(續) 在10.8m，9m，5.4m，1.8m下經過不同時間后的溫度值

由表3數據，繪制特定高度下，時間不斷增大各高度具體溫度值的曲線。發現高度越高，其越容易達到0.6Mpa對應飽和溫度138.73K。曲線斜率隨高度降低而不斷減小，即高度越高，溫度變化越快。溫度變化規律見圖4：

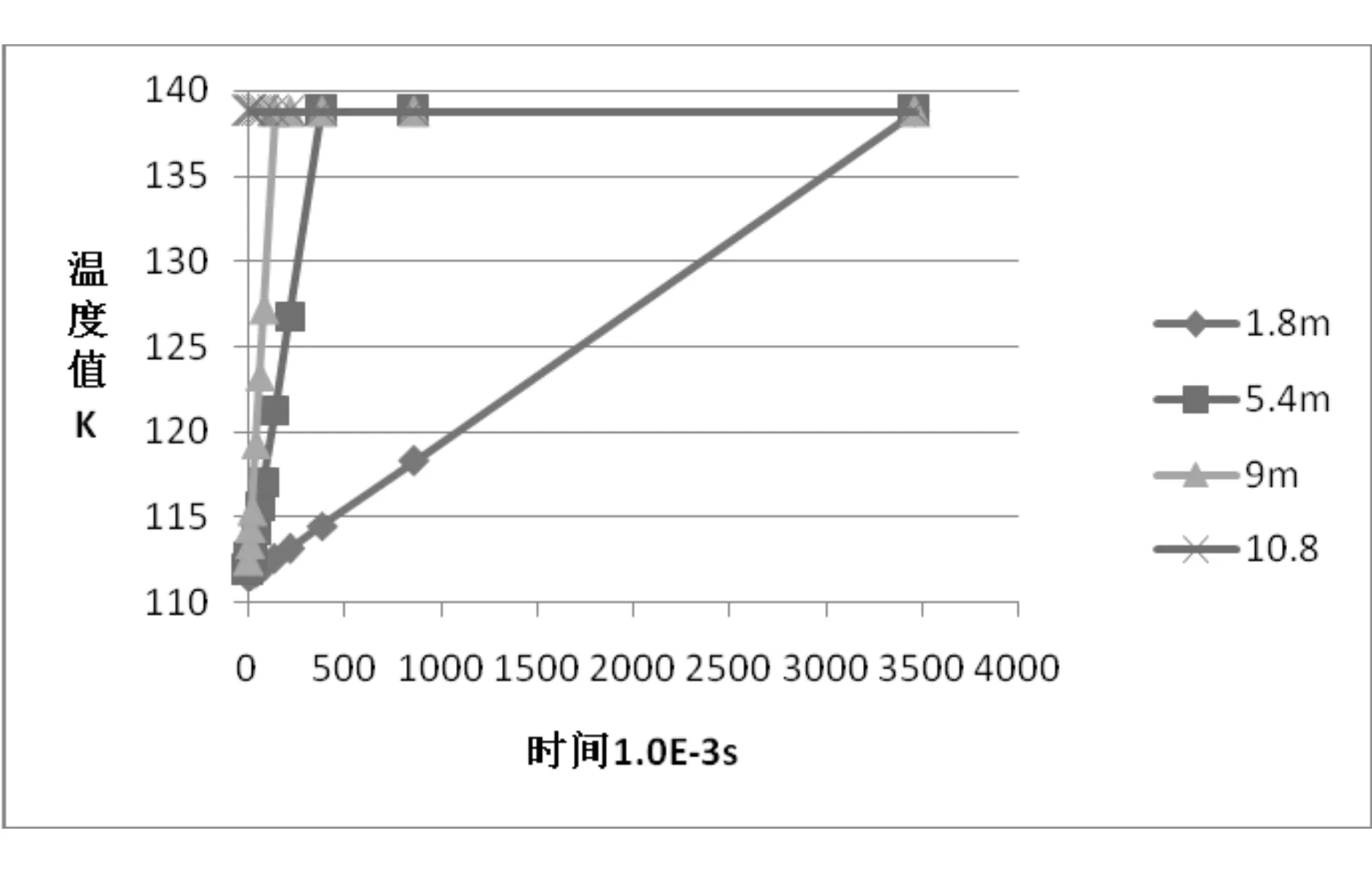
圖4 經過不同時間，特定高度溫度值

3.4 純甲烷從整體初態0.1Mpa達到0.6Mpa所耗用時間

為了使得LNG儲罐內頂部的氣腔內的壓力由0.1Mpa上升到0.6Mpa，那么就需要有5倍于上部氣腔的氣體質量汽化，即這產生的5倍汽化氣體所吸收的熱量全部來自液化天然氣儲罐漏熱。同時在這一過程中，忽略液體減少而使氣體體積的增大量。

下式中m初表示開始狀態時氣腔部分的質量。

在0.1Mpa時，汽化潛熱 h=511.2KJ/Kg

ρ初=1.7946Kg/m3

在0.6Mpa時，汽化潛熱 h=448.84KJ/Kg

所以根據：qwAt=5m初h

由于在這一加熱過程中，溫度是隨時改變的，壓力也是在0.1Mpa至0.6Mpa之間不斷變化的，而汽化潛熱值是壓力的函數，因為我們不能得到單位時間步長下的壓力變化范圍，所以不能對汽化潛熱值的值進行精確計算，這里，用0.1Mpa，0.6Mpa兩個端點的汽化潛熱的平均數作為這一過程中的恒定汽化潛熱值。

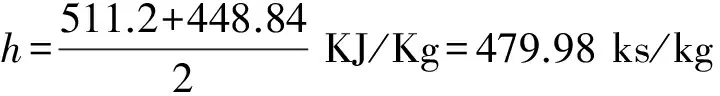
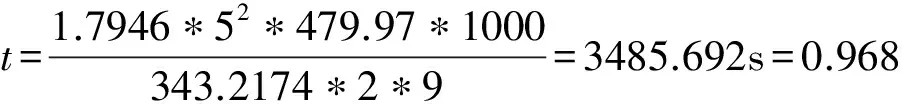
4 結語

通過計算結果分析，可以得出以下結論：

(1)隨時間變化，氣液分界面處的溫度會一直保持不變，即為138.73K，而其他較低高度下隨著時間增大都會相繼達到138.73K，當時間大于0.968小時，整個溫度場會變為均勻場，即都達到0.6Mpa對應的飽和狀態。

(2)經過相同時間，液相區上部的溫度值較大，熱流更多的向上流動。同一時刻，儲罐內溫度呈上高下低的特點。

(3)不同高度下，液相區的溫度值不斷增大，最終都會到達并保持138.73K不變。我們發現高度越高，其達到0.6Mpa對應飽和溫度的時間越短。

(4)經前文計算，我們得出儲罐內汽相區壓力由0.1Mpa達到0.6Mpa所需的時間是0.968小時。說明在儲罐壁面漏熱情況下，由于分層現象的存在，儲罐內純甲烷升溫速度較快。

上述低溫分層溫度分布規律和已有大量文獻研究結論吻合，該分層幾何模型與數學模型基礎上所得溫度分布解析解是有價值的，起到為將來進行大量數值模擬提供參考對比的實際意義。

[1] 程棟，顧安忠.液化天然氣的貯存分層現象[J].深冷技術，1997(1)：13-15.

[2] 李品友，顧安忠.液化天然氣貯存非穩定性的理論研究[J].中國學術期刊文摘(科學快報)，1999，5(2)：170-172.

[3] 林文勝，顧安忠，李品友.液化天然氣的分層與漩渦研究進展[J].真空與低溫，2000，6(3)：125-132.

[4] 程向華，厲彥忠，陳二鋒.火箭液氧貯箱熱分層現象數值模擬[J].低溫工程，2008，162(2)：10-13.

[5] 程向華，厲彥忠，陳二鋒，等.新型運載火箭射前預冷液氧貯箱熱分層的數值研究[J].陜西：西安交通大學學報，2008，42(9)：1132-1136.

[6] Cheng Xianghua，Li Yanzhong，Chen Erfeng， et al .Effect of return inlet on thermal stratification in a rocket tank[J].Journal of Thermo-physics and Heat Transfer，2010，24(1)：112-122.

[7] 程向華，厲彥忠.低溫液體熱分層特性分析[J].低溫工程，2011,183(5)：50-55.

[8] 江帆，黃鵬.Fluent高級應用與實例分析 [M].北京：清華大學出版社，2008(7),73-138.

[9] 張凱，王瑞金，王剛.Fluent技術基礎與應用實例 [M].北京：清華大學出版社，2010.9,125-137.

[10] 游立新，顧安忠.液化天然氣的分層和漩渦及防止措施[J].石油與天然氣化工，1991,20(3)：21-25.

[11] 李品友，顧安忠.LNG渦旋及預防措施[J].低溫與特氣，1998,(2):54-57.

[12] 李品友，顧安忠.液化天然氣渦旋的理論研究[C]. 水動力學研究與進展(A輯)， 2000，15(2)：182-190.